基于科赫雪花图形激励装置的涡流传感器工作原理分析*
陈国龙,张卫民,庞炜涵,秦 峰,果 艳,王 超
(北京理工大学机械与车辆学院,北京100081)
基于科赫雪花图形激励装置的涡流传感器工作原理分析*
陈国龙,张卫民*,庞炜涵,秦 峰,果 艳,王 超
(北京理工大学机械与车辆学院,北京100081)
首次提出并设计了一种基于分形理论自相似结构的科赫雪花图形激励装置涡流传感器,对这种传感器的工作原理和物理模型进行了深入的分析,分析表明,基于分形结构激励线圈的涡流传感器,在多处具有涡流叠加效应,随着科赫雪花图形阶次的提高,这种涡流叠加效应越来越明显,分布密度不断增加,可以显著提高涡流传感器激励效果和检测灵敏度,从而提高对微小裂纹缺陷的检测能力。研制了实际装置,通过实验证了这一结论。
无损检测;涡流检测;分形几何;科赫曲线
涡流检测利用电磁感应检测原理来工作,具有检测速度快、使用方便等特点,是五大常规检测方法之一,在航空航天、交通电力、核工业等重要场合有着广泛应用,对于保障工业设备安全,起着十分重要的作用[1-3]。近年来,涡流检测技术获得了长足的进步,脉冲涡流检测技术[4-9]、远场涡流检测技术[10-12]、阵列涡流检测[13-14]技术的实现,有力提高了这项技术的检测能力,使涡流检测技术获得了新的更广泛应用。
与此同时,对传统结构涡流传感器进行改进,使其进一步提高激励、接收环节的各项技术性能,也是一种可行的技术途径。
本文首次提出并研制了一种涡流传感器新型结构,该结构运用分形几何学中的科赫雪花图形[15-16]作为激励线圈,有效提高了激励涡流场的密度,从而进一步提高了涡流传感器检测灵敏度。本文尝试从理论上分析其工作机理,并建立该系统分析模型。
1 基于科赫雪花图形激励装置涡流传感器的基本构成
传感器的基本构成如图1所示,传感器采用发射接收分离模式,激励线圈由二次科赫雪花图形组成,分布在一层电路板上,科赫雪花图形是一种典型的分形曲线,通过迭代函数系统不断迭代产生。其具体生成过程是:输入初始子,即一个等边三角形和迭代次数n;将等边三角形的每个边三等份,以中间份为基础向外构造一个等边三角形,然后删除中间份,完成一次迭代,再重复该步骤n-1次;输出完成迭代后的图形。本文采用的原型传感器设计时,输入的初始子等边三角形的边长为20 mm,迭代次数为2次,其输出结果是由等长的48条线段组成的2次科赫曲线。传感器接收线圈采用阿基米德螺线构成,为了增加传感器的灵敏度,在不同层级电路板上布置了多圈结构。
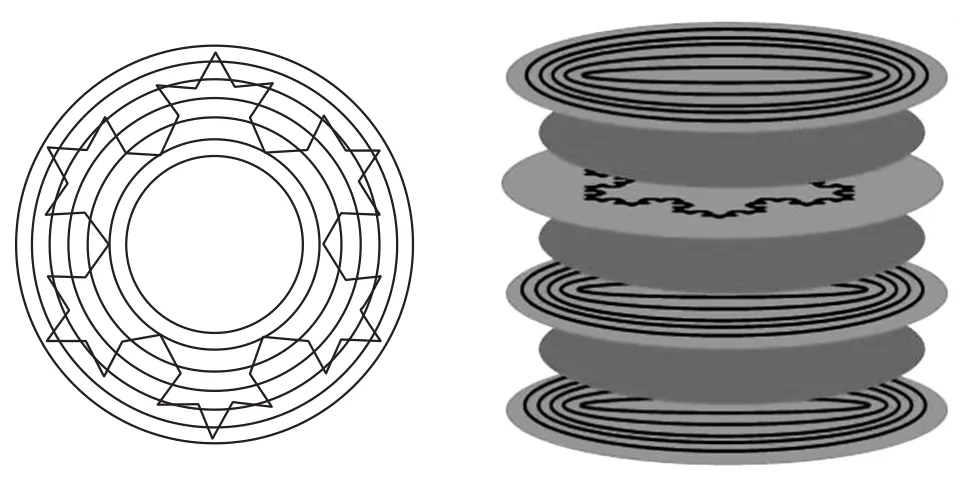
图1 基于科赫雪花图形激励装置的涡流传感器
该传感器为平面结构,可由普通PCB板制成或由柔性电路板制成,工作时可安放在重要结构上,实现在位监测,在健康监测领域具有较好的应用潜力。在本例中,传感器激励线圈是采用输出的48个点的坐标来布线而成,线宽采用12 mil,布置在PCB板的第二层上。而信号拾取线圈布置在PCB板上的第一、二、四层中的阿基米德螺线构成,其线宽和线间距都是8 mil,并通过过孔连在一起。
2 基于科赫雪花图形激励装置涡流传感器工作原理分析
该传感器的结构特点是由很多线段线构成,这些线段以不同角度叠加,从而是各自的感应涡流场叠加,从而提高了传感器激励涡流场的密度,而这对提高传感器的检测灵敏度是有利的。为不失问题一般性,取一个局部进行分析。
如图2所示,传感器的基本单元为某一平面的有限长直线电流源,根据比奥萨法尔定律,XOY平面内有限长直线电流源在空间中的磁场分布遵循如下基本公式[17]:

具体可做如下假设,AB为位于XOY平面内长度为d,电流强度为I的有限长直线电流源;P为场点,即所求磁场分布点的位置。规定场点到电流源的起始点的向量为γ1=PA,场点到电流源的终点的向量为 γ2=PB,电流源的始末两点之间向量为I=AB,θ2为γ2与γ向量之间夹角的补角,θ2为γ2与γ向量之间夹角的补角,为γ的单位矢量。
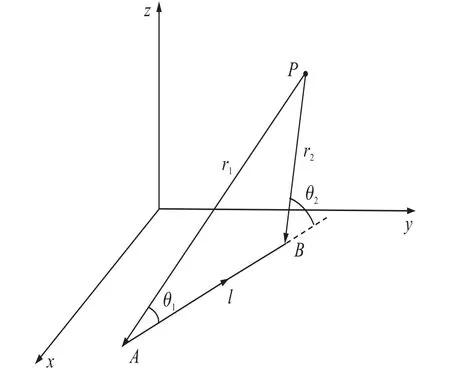
图2 有限长直线电流源模型
由于有限长直线电流源产生的磁场在空间中的分布具有圆柱对称性,其对称轴为电流源AB,也就是说,对于空间中任意一点,均可通过AB轴线找到一点与其具有对称性,而且这两点的磁感应强度的大小是相等的,而方向与AB轴线呈右手螺旋关系。为了简化问题,首先求解位于XOY平面内的P点出的磁感应强度,再通过引入矢量的方向将求解的结果拓展到三维空间的场点。

图3 简化为二维问题模型
进一步将上述问题简化后的二维模型,图中的P点相对于AB轴线具有旋转对称性。则P点的磁感应强度为
由图中的几何关系可以得到,
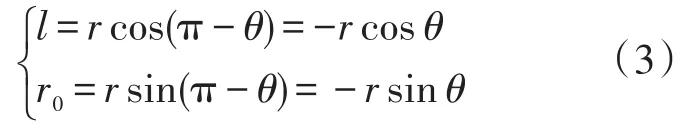
上式消去r,得到l=-r0ctgθ,取微分可以得到,进一步推导得到[18],
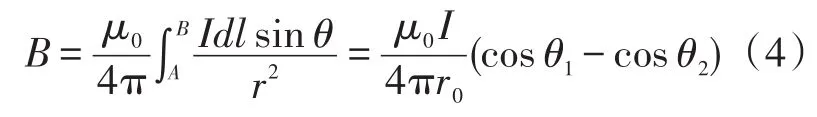
上式是磁场的一个标量表达式,其方向为z方向。在XOY平面内,该方向垂直与该平面。
考虑到求解的磁场为三维空间中除电流源以外的空间点的磁感应强度,磁感应强度的方向由dl×r决定,其方向可用单位矢量的方向表示。所以三维空间中有限电流源产生的磁场可以表示为,
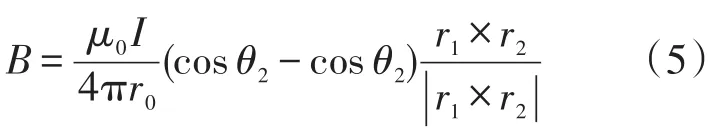
在PAB三角形中,可以进一步将上式简化为

对于在XOY平面内多线段组成的任意多边形在空间中产生的磁场分布,如图4所示。由n个有限长直线电流源组成的多边形中,设其第i个边的电流流入点为Ai,流出点为Bi,边长di,场点到流入点矢量为ri1,ri1与电流源矢量夹角为cosθi2,场点到流出点矢量为ri2,ri2与电流源矢量夹角为cosθi2。根据磁场的叠加原理,任意多边性电流源在空间中产生的磁场计算表达式可以表示为
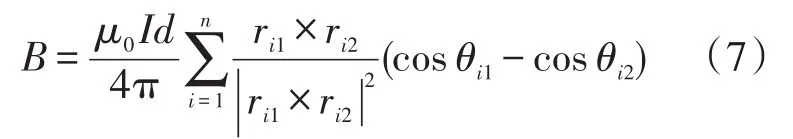
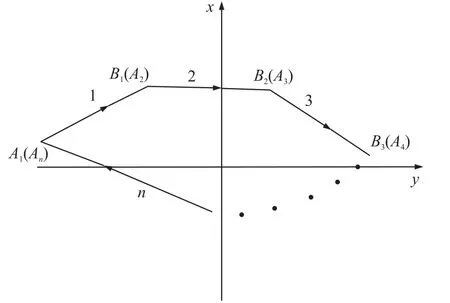
图4 任意多边形电流源磁场分布
将上述算法编制成程序,对二阶科赫雪花激励装置传感器和传统圆形线圈传感器进行分析对比,可以发现科赫雪花装置由于存在涡流叠加作用而使激励场有所增强。

图5 科赫雪花激励装置传感器磁场分布图
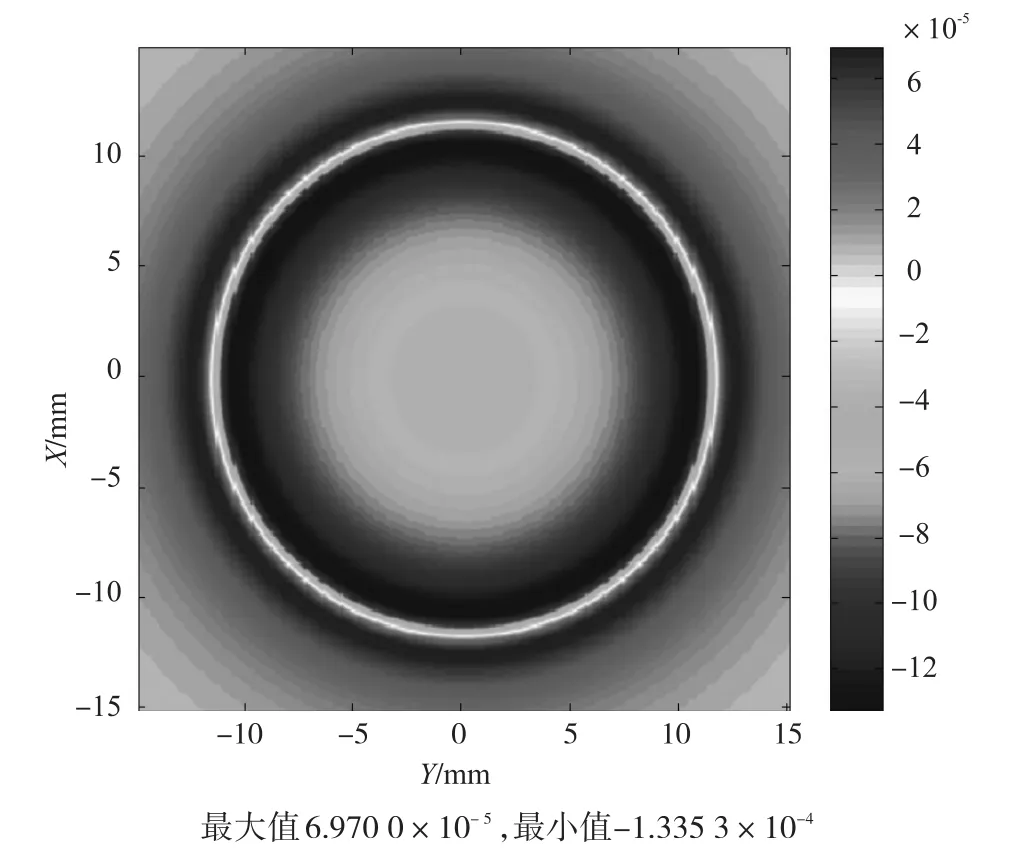
图6 传统圆形线圈激励装置传感器磁场分布图
3 基于科赫雪花图形激励装置涡流传感器的缺陷检测实验分析
3.1 实验装置
设计了验证科赫雪花激励装置涡流传感器检测微细裂纹的实验系统验证检测能力。激励模块主要由函数发生器RIGOL GD1022和功率放大器LP05组成,其输出的最大电流为1 A,频带范围为直流到1 MHz。实际试验中激励电流为400 mA,频率为1 MHz。传感器接收装置采用了乘法器和锁相环装置[19],其前置放大器采用性能优秀的特殊差动放大器仪表放大器AD624,并设计选通开关来调节其不同的放大倍数,分别为100,200,500和1 000倍,后续对裂纹信号的数字滤波与显示等数字信号处理由MATLAB完成。
被测裂纹尺寸分别为20 mm×0.3 mm×0.12 mm,20 mm×0.3 mm×0.15 mm,是通过本实验开发的电火花刻伤机蚀刻而成,在测量尺度上属于微细裂纹尺度范围。检测时传感器安装在三维扫查台上,沿着垂直于裂纹并经过裂纹中心的轨迹扫查。扫查过程中传感器的提离高度为0.1 mm,检测系统组成和实物如图7、图8组成,检测结果如图9、图10所示,左侧为原始图,右侧为经过低通滤波器处理后比较清晰的图像,可以发现裂纹信号有一个明显的峰值特征。

图7 实验系统原理图

图8 实验系统实物图
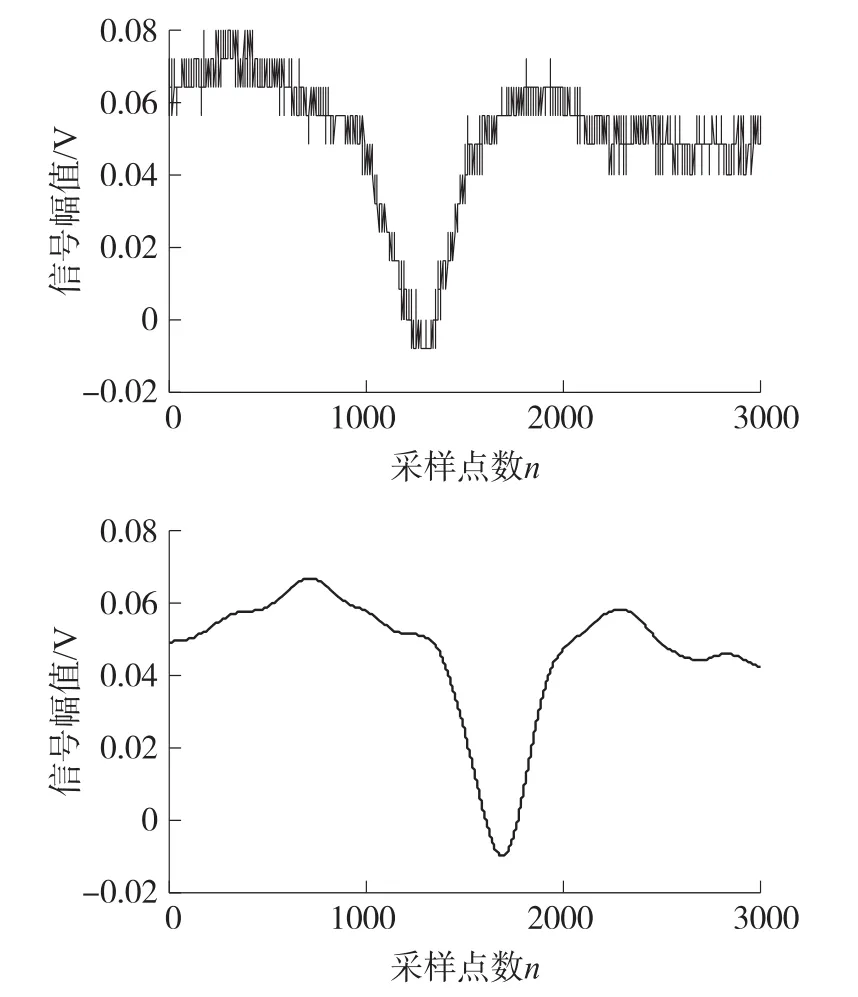
图9 20 mm×0.3 mm×0.12 mm裂纹初始信号与数字滤波后信号
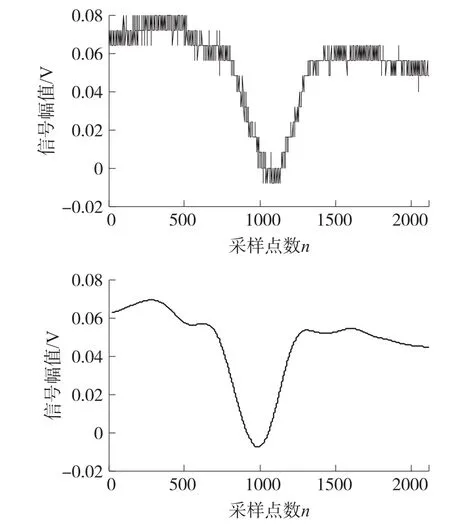
图10 20 mm×0.3 mm×0.15 mm裂纹初始信号与数字滤波后信号
4 小结
提出并研制了一种科赫雪花图形激励装置传感器,初步分析了这种传感器的理论模型,实测表明,这种传感器,对金属表面微细裂纹有较好的识别能力,由于这种传感器属于一种平面型传感器,便于制成柔性结构和智能夹层结构,在金属疲劳裂纹扩展在位监测中具有较好应用前景。
[1]García-Martín J,Gómez-Gil J,Vázquez-Sánchez E.Non-Destruc⁃tive Techniques Based on Eddy Current Testing[J].Sensors,2011,11(3):2525-2565.
[2]Auld B,Moulder J.Review of Advances in Quantitative Eddy Cur⁃rent Nondestructive Evaluation[J].Journal of Nondestructive Evaluation,1999,18(1):3-36.
[3]Tumanski S.Induction Coil Sensors-A Review[J].Measurement Science and Technology,2007,18(3):R31.
[4]Abidin I Z,Mandache C,Tian G Y,et al.Pulsed Eddy Current Testing with Variable Duty Cycle on Rivet Joints[J].NDT&E In⁃ternational,2009,42(7):599-605.
[5]Arjun V,Sasi B,Rao B P C,et al.Optimisation of Pulsed Eddy Current Probe for Detection of Sub-Surface Defects in Stainless Steel Plates[J].Sensors and Actuators A:Physical,2015,226:69-75.
[6]He Y,Luo F,Pan M,et al.Defect Classification Based on Rectan⁃gular Pulsed Eddy Current Sensor in Different Directions[J].Sen⁃sors and Actuators A:Physical,2010,157(1):26-31.
[7]何赟泽,罗飞路,胡祥超,等.脉冲涡流矩形传感器的多维信号特征分析与缺陷识别[J].传感技术学报,2009,22(5):680-683.
[8]焦胜博,丁华,何宇廷,等.基于半解析模型的花萼状涡流传感器损伤监测灵敏度分析[J].传感技术学报,2013,26(2):205-210.
[9]贾永平,丁天怀,王鹏.曲面体间隙电涡流检测的有限元分析[J].传感技术学报,2005,18(2):221-224.
[10]Kim D,Udpa L,Udpa S.Remote Field Eddy Current Testing for Detection of Stress Corrosion Cracks in Gas Transmission Pipe⁃lines[J].Materials Letters,2004,58(15):2102-2104.
[11]Lord W,Sun Y,Udpa S,et al.A Finite Element Study of the Re⁃mote Field Eddy Current Phenomenon[J].Magnetics,IEEE Transactions on,1988,24(1):435-438.
[12]Xu X,Liu M,Zhang Z,et al.A Novel High Sensitivity Sensor for Remote Field Eddy Current Non-Destructive Testing Based on Or⁃thogonal Magnetic Field[J].Sensors,2014,14(12):24098-24115.
[13]Chen X,Ding T.Flexible Eddy Current Sensor Array for Proximi⁃ty Sensing[J].Sensors and Actuators A:Physical,2007,135(1):126-130.
[14]Huang H,Sakurai N,Takagi T,et al.Design of an Eddy-Current Array Probe for Crack Sizing in Steam Generator Tubes[J].NDT &E International,2003,36(7):515-522.
[15]Cohen N.Fractal Antenna Ground Counterpoise,Ground Planes and Loading Elements.Google Patents,2000.
[16]Werner D H,Ganguly S.An Overview of Fractal Antenna Engi⁃neering Research[J].Antennas and Propagation Magazine,IEEE,2003,45(1):38-57.
[17]张三慧.大学物理学:电磁学.第三册[M].第3版.北京:清华大学出版社有限公司,1999.
[18]岑敏锐.任意多边形平面载流线圈磁场的空间分布[J].武汉工程大学学报,2010(1):104-106.
[19]张丹,刘新华,张家亮.一种适用于微弱传感信号检测的锁相放大电路[J].Computer Engineering and Applications,2013,49(15):210-214.

陈国龙(1987-),男,博士生。北京理工大学机械与车辆学院,机械工程。主要研究方向为电磁无损检测;

张卫民(1964-),男,北京理工大学机械与车辆学院,教授,博士生导师。1982.09~1986.07大连理工大学机械制造工程系,获学士学位;1986.09~1988,10大连理工大学机械工程系,硕士研究生;1988.10~1989.10北京语言学院出国培训部,学习;1989.12~1994.10乌克兰(前苏联)基辅工学院仪器制造系,获博士学位。
Analysis on the Working Principle of Eddy Current Probe Using the Koch Curve Exciting Coils*
CHEN Guolong,ZHANG Weimin*,PANG Weiha,QIN Feng,GUO Yan,WANG Chao
(School of Mechanical Engineering,Beijing Institute of Technology,Beijing 100801,China)
An eddy current probe using self-similarity fractal structure Koch curve excting coils is first proposed.Its working principle and theoretical model are deeply analyzed.The analysis shows that,due to eddy current counter effect in multiple places,the counter effect becomes more apparent and the eddy current density becomes stronger,with increasing stage of Koch curve.The exciting result and the sensitivity of eddy current probe are significantly improved,so the detection capability for micro-defect is improved.These results are validated by experiments of real system.
NDT;eddy current testing;fractal geometry;Koch curve
TG115.28
A
1004-1699(2015)10-1454-05
��0550;2140;5210;6110
10.3969/j.issn.1004-1699.2015.10.006
项目来源:国家教育部高等学校博士学科点专项科研基金课题项目(20121101110018);北京理工大学研究生科技创新活动专项计划项目(2015CX10014)
2015-05-15 修改日期:2015-06-23

