用刚性表面球形传声器阵列重构入射波声场与识别定位声源*
李敏宗,卢奂采,2*,金江明
(1.浙江工业大学机械工程学院,特种装备制造与先进加工技术教育部/浙江省重点实验室,杭州310014;2.浙江工业大学,浙江省信号处理重点实验室,杭州310014)
用刚性表面球形传声器阵列重构入射波声场与识别定位声源*
李敏宗1,卢奂采1,2*,金江明1
(1.浙江工业大学机械工程学院,特种装备制造与先进加工技术教育部/浙江省重点实验室,杭州310014;2.浙江工业大学,浙江省信号处理重点实验室,杭州310014)
刚性表面球形传声器阵列是测量三维声场常用的前端,由于刚性球面对入射波声场有散射影响,直接测量值不是原入射波声场的声压值,因而不能使用在自由声场条件下建立的声场模型和近场声全息方法来重构入射波声场。通过刚性球体表面声波散射的数学模型,建立起入射波声压与发生散射后总声压之间的关系,进而通过刚性表面球形传声器阵列测量声压,计算入射波声场分布,并进行声源识别定位。通过仿真与实验,检验了球面入射波遇到刚性表面球体发生散射后,球体表面处声压分布的变化。由球面近场声全息方法,重构球形阵列表面及外部空间的入射波声场,检验了波数、重构距离参数变化对声场重构精度的影响。结果表明:采用刚性表面球形传声器阵列测得的声场总声压,运用根据声波散射模型建立的球面近场声全息方法,可以以一定的精度重构出入射波声场的三维空间分布。
球形传声器阵列;入射波声场重构;球面近场声全息;声波散射;刚性表面球体
球形传声器阵列,由于其球面所具有的经纬角全指向性和三维对称性,能够测量声压场的三维空间分布,因而对于封闭空间(如飞机、汽车和房间内部)的声场重构、声源识别定位等应用,具有独特优势[1-5]。球形传声器阵列是指在一个固定半径的球面上按照一定的几何规律和优化准则[6],布置一组传声器而形成的声场全息声压测量阵列。按照结构可以分为空心球形阵列与刚性表面球形阵列,空心球形阵列指的是将各个传声器固定在指定的位置,传声器的表面形成一个虚拟球面的若干个节点,它的声场理论模型假设声场不受阵列影响,然而在应用时由于声场中引入了传声器支架与导线等因素,实际上(尤其在声音频率较高时)满足不了此假设条件[3]。刚性表面球形阵列是指将传声器镶嵌到具有刚性表面的球面壳体上,由于刚性表面对入射声波产生的散射,球形阵列上传声器测量的声压值,不是原入射波声场的声压值,因此不能直接将其应用于自由声场条件下建立的声场模型和近场声全息方法,来重构入射波声场,而需要考虑球形传声器阵列的刚性表面在声场中发生的散射现象,建立考虑散射现象的声场的数学模型。所幸的是,刚性表面球体对入射波声场的散射在声学领域是一个经典问题,其理论分析与数值计算结果在理论声学相关专著中[7-9]均具有阐述,本文以入射波在刚性球形表面产生散射的数学模型为基础,推导对应的球面近场声全息算法,最终由刚性表面球形阵列上传声器所测得的声场总声压数据,重构出阵列周围空间的入射波声压的三维空间分布,进而进行声源识别定位。
目前,刚性表面球形传声器阵列多用于远场测试,结合波束形成方法[10-12]进行三维空间的声源识别定位。由于刚性表面球形传声器阵列在近场可结合近场声全息方法进行声场重构,在球状或类似于球状的内部封闭空间中的声源识别定位有独特优势,故在该方向的研究也有一定进展。2008年,Finn Jacob⁃sen[2]在球面近场声全息方法中,考虑了刚性表面球形传声器阵列的声波散射影响,在仿真中给出了阵列中心与声源连线上的重构声压分布,将其与基准声压进行了对比,并在实验中比较了空间中单个点位置处的重构声压与测量声压的幅值,但没有进行三维空间的声场重构误差的分析与声源识别定位的验证;2010年,Earl G.Williams[3]使用刚性表面球形传声器阵列,进行了声场重构的研究,在不同半径的重构球面上,进行了三维空间的声场重构误差分析,并在点声源的声场环境下,进行了声场重构与声源识别定位的验证,其论文也通过考虑刚性球面的散射模型,得出了修正的传播因子,但根据此修正传播因子计算出的声场为阵列表面及外部空间声场的总声压分布,而不是仅仅由入射波形成的声场的声压分布。本文的研究内容为:在球面近场声全息方法中应用刚性球面的声波散射模型,计算出重构的入射波声压在整个三维空间的分布,并在不同波数下,进行不同半径的重构球面上声场重构误差分析;通过重构出的三维空间入射波声压分布,进行三维空间的声源识别定位,并使用刚性表面球形传声器阵列进行实验验证。
本文首先在第1节中根据刚性球面发生声波散射的Neumann边界条件,建立声波散射数学模型,进而得出刚性球面散射前入射波声压与散射后总声压之间的数学关系。通过仿真,检验球面入射波遇到刚性表面球形传声器阵列时发生散射后的声场变化规律。然后在第2节中,将检验由球形传声器阵列测量的散射后总声压,通过球面近场声全息方法,重构入射波形成的声场,以及参数对重构精度的影响。最后在第3节中给出结论。
1 刚性球体表面声波散射的数学模型
1.1 刚性表面球体引起声波散射的数学模型
在各向同性声传播介质中,入射声波可由Helmholtz方程的解的形式表示为:
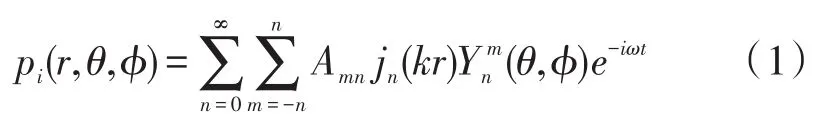
式中:(r,θ,ϕ)为声场中任意一点的球坐标,pi为此点处入射波的声压,ω表示角频率,k为波数(k=ω/c,c为声音在空气介质中的传播速度),t表示时间。jn(kr)为球贝塞尔函数,表示声场径向即r方向的解;为球谐函数,表示声场θ和ϕ方向的解;Amn为波动方程特解的系数。对于稳态声场,可将时间依赖性因子e-iωt略去。
假设在声场空间中放置一个半径为a的刚性表面球体,其球心与坐标系原点重合,则刚性球体表面会引起入射波的散射现象,并且球面所发出散射声波的频率与入射波的频率相同。声场总声压 pt由入射波的声压pi与散射波的声压ps叠加而成:

刚性球体表面向外辐射的散射声波可表示为:
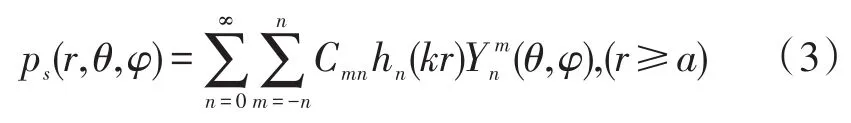
其中hn(kr)为第一类球汉克尔函数,Cmn为球谐函数的系数。
由于刚性球体表面不会吸收入射波的能量,故将其完全散射出去。同时,刚性球面也不会由于散射而变形,因此,球面处的法向介质粒子速度即总声压的梯度为零,刚性球面发生散射的Neumann边界条件[7-9]可由下式表示:
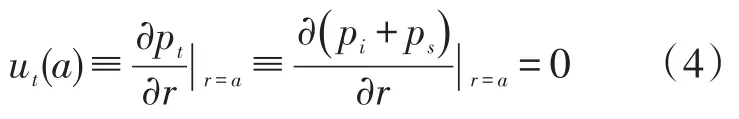
其中,ut(a)表示刚性球面上的法向介质粒子速度,将其结合于公式(1)与公式(3)可得出:
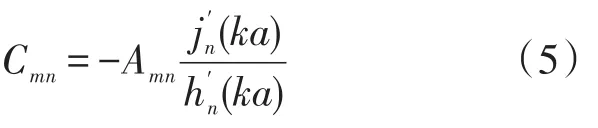
式中:‘′’为求导符号。从而散射波的声压ps,可以表示为:

于是,根据公式(1)可得到声场总声压(pt)为:

在这里,根据刚性球面的Neumann边界条件得出散射波与入射波的关系,从而进一步得出经过刚性表面球体散射之后的总声场模型。对于镶嵌在刚性表面球形阵列上的传声器,在应用中测得的是散射后的声场总声压,根据式(1)与式(7)即可计算出发生散射前的入射波声场声压。
1.2 刚性表面球体引起声波散射后声场的变化
对于刚性表面球形传声器阵列,各传声器都镶嵌在球体的刚性表面上,测量与记录声场的声压。因此,研究球形传声器阵列表面处发生的散射现象,对于运用球形传声器阵列测量声压,进行近场声全息或其它用途的声学计算分析具有重要意义。本小节对球面入射波声场进行分析,先给出球面波声场声压的球谐函数展开形式的解析公式,然后检验球面入射波在遇到刚性表面球形传声器阵列时,散射发生前后球体表面处声压分布的变化。
假设球面波由(rs,θs,ϕs)处单极子点声源发出,则空间中任意一点(r,θ,ϕ)处的声压可以表示为[13]:

其中符号‘*’表示复数共轭,ρ为介质的密度,Qs为球面波声源强度,N为球谐函数的截止项数,在本文中取N=30。式中r<表示r与rs两者中取值较小者,r>表示r与rs两者中取值较大者。

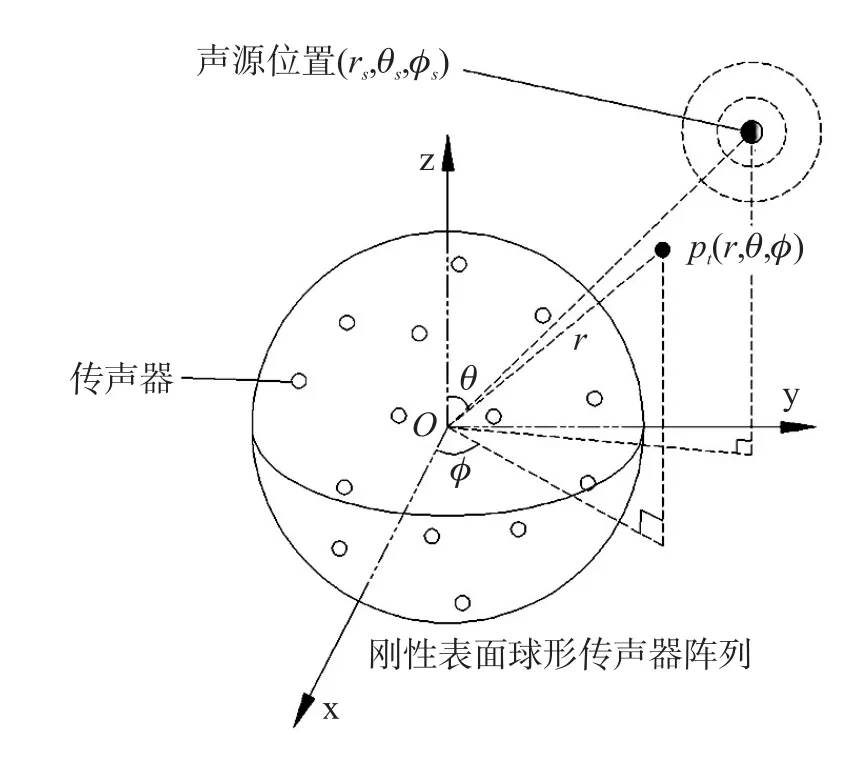
图1 刚性表面球形传声器阵列与球面入射波示意图

图2 球面入射波声场中球形传声器阵列刚性表面(r=a)处声压分布图。入射波为来自位于点(r0,θ,φ)=(0.4 m,π/2,π)发出的球面波。(ka=5,a=0.2 m)
设置阵列半径a为0.2 m,球面波声场由一个位于(rs,θs,ϕs)=(0.4 m,π/2,π)处的单极子声源生成,无量纲频率(dimensionless frequency)ka为5。在上述参数下,得出球面的声压分布如图2所示。在空间中不存在障碍物时,虚拟球面(r=a)的声压分布如图2(a)),声压值在正对声源处最大,在背对声源处最小,球面上声压值的变化较为平缓;而当刚性表面球形传声器阵列存在时,球面声压分布如图2(b)),在正对声源的球面区域,总声压增大且有最大峰值,其它处的声压值则迅速减小,并且在背对声源处的声压分布有一个突起。
2 入射波声场的重构
本节将刚性球体表面散射模型应用于球面近场声全息方法中,通过仿真和实验检验由刚性表面球形阵列上传声器测量的散射后总声压,重构由入射波单独形成的声场,以及参数对重构精度影响。
2.1 球面近场声全息方法
球面近场声全息方法[1-5],由布置于球形阵列上传声器所测得的声压,通过声场逆向空间变换,重构出处于近场空间或声源结构表面的声学量分布。声场重构公式如下:
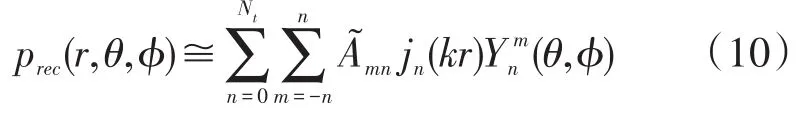
式中:prec(r,θ,ϕ)为位置(r,θ,ϕ)处的重构声压,Nt为基函数截止项数,取值与传声器数目相关,A~mn为未知系数。
对于刚性表面球形传声器阵列,基于考虑刚性球面对入射波的散射影响的声场模型,可重构出散射前的入射波声场。根据第1.1节中入射波声场与总声场的关系,即公式(7),可得出系数A~mn为:
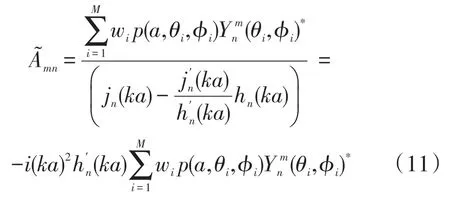
式中:p(a,θi,ϕi)为第i个传声器坐标处的声压值;wi为该点相应的权重,由球面数值积分方法确定;M为传声器的数目。
2.2 入射波声场重构的仿真
上节中介绍了使用刚性表面球形传声器阵列测量的声场总声压,重构入射波声场的球面近场声全息方法和数学模型,本节将检验各参数对声场重构精度的影响。
设置声场环境由一个位于(r0,θ,ϕ)=(0.5 m,π/2,π)处的单极子声源生成;刚性表面球形传声器阵列位于坐标系原点,阵列半径a=0.2 m,传声器数目为M=64。球形阵列上各传声器在根据公式(9)测得总声压数据,引入信噪比为40 dB的随机测量噪声,再使用这些带有随机测量噪声的总声压数据,运用球面近场声全息理论,进行声场重构计算。由式(10)与式(11),可重构出空间中任意一点处的入射波声压prec(r,θ,ϕ),再将其与相同位置的声压理论值pthe(r,θ,ϕ)(由公式(8)得出)进行比较。在本文中将重构一个以球形阵列中心为球心的球面(a≤R≤rs,其中R为重构球面的半径)上的声压分布,在此球面上均匀的取出Q点,声压在这些点的归一化最小二乘(normalized least-squares)重构误差[14]定义为ε:
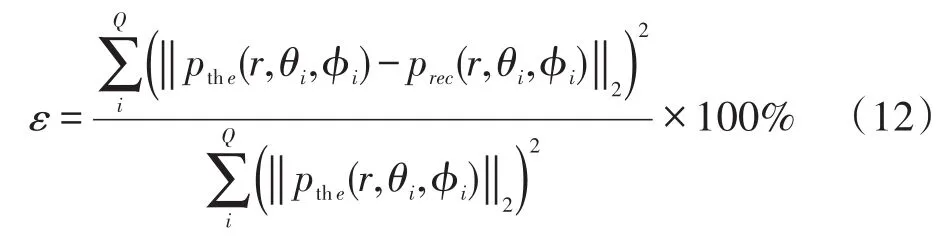
式中:‖∙‖2表示二范数。
图3为在波数k=15下,球形阵列表面上重构的入射波声压分布,其与入射波声压理论值的误差为ε=0.28%。可见,采用考虑了球面散射模型的球面近场声全息方法,在阵列表面处重构的声场声压分布,可以达到非常高的重构精度。
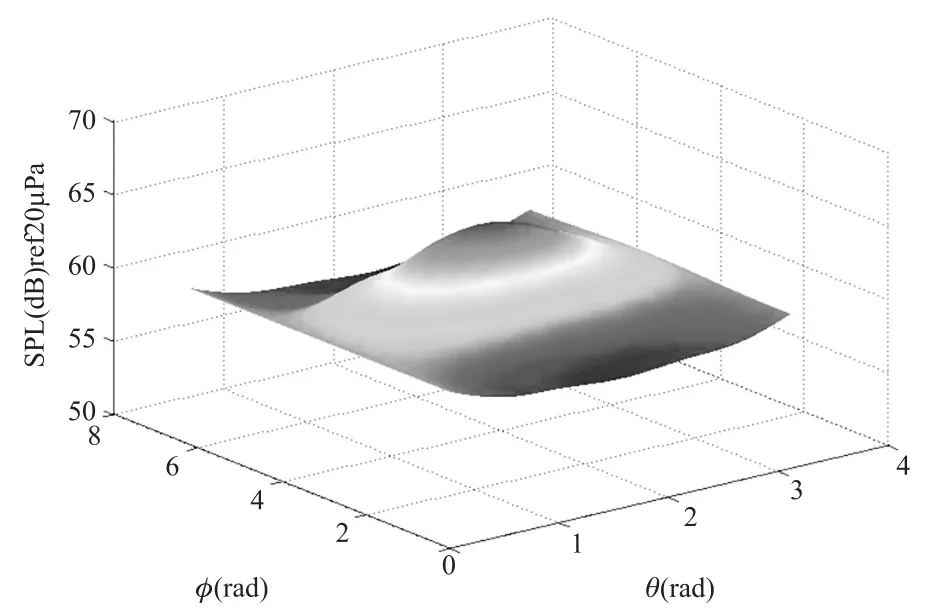
图3 球面近场声全息方法重构出的球形阵列表面入射波声压分布(a=0.2 m,k=15,M=64,R=0.2 m SNR=40 dB)
由图3的结果得出,球面近场声全息方法可重构出球形阵列表面处声压分布。而在实际应用中,需要重构球形阵列外部空间的入射波声压分布,以作为声源识别定位的依据。图4为波数分别为k=5、k=15、k= 25时,重构误差ε随着重构半径R增大的变化。

图4 在不同波数下声压重构误差随重构球面半径的变化(a=0.2 m,M=64,SNR=40 dB)
由图4可见,在考虑了刚性球体表面声波散射的入射波声场重构计算中,当声压测量信号的信噪比为SNR=40 dB和球形阵列的传声器数目M=64时,重构半径R由0.2 m增大至0.25 m的范围内,在波数k分别为5、15、25的情形下,重构误差ε均在10%以下,这说明在球形阵列外部较近的区域,声场重构能取得较高的精度。这是因为球形阵列测得了足够多的由重构球面传播来的声场近场信息。随着重构半径R的增大,即重构球面与声源之间距离的减小,重构误差ε也随之增大,特别是当波数k较大时,重构误差ε随重构半径R增大而急剧增大,比如在波数k为25的情形下,重构半径R由0.2 m增大至0.5 m时,重构误差由2.3%增大至90%,这是因为重构半径R越大,球形阵列采集到由重构球面传播来的近场信息即高波数信息越少,因而重构误差ε越大。而当波数k较小时,重构误差ε则随重构半径R增大较缓慢地增大。如图4所示,当重构半径R由0.2 m增大至0.5 m范围内,在波数k为15时,重构误差由0.4%增大至69.2%,而在波数k为5时,重构误差仅由0.1%增大至23.7%,这是因为当波数较小时,即使重构半径R较大,球形阵列依然采集到了足够的由重构球面传播来的近场信息,因而重构误差ε相对较小。
图5为波数k=15,重构半径R=0.5m,即声源所在重构球面处的入射波声压分布图,图5(a))为由球面近场声全息方法重构的入射波声压分布,图5(b))为根据公式(12)得出的入射波声压理论值的分布。此情形下,由于波数k及重构半径R较大,因而重构误差ε较大,为69.2%。但是,依然可以通过重构的入射波声压分布图,明显识别出声源的方位为(π/2,π)。
上述研究结果表明,使用球面近场声全息方法进行入射波声场的重构,在刚性表面球形阵列较近的区域,有较高的重构精度,在球形阵列表面上的重构精度最高。当声源辐射含有较高的波数k的情形下,在球形阵列测量总声压的信噪比SNR和阵列传声器数目M不变时,可将球形阵列尽量置于声源的附近,即缩短重构半径R,声源近场的入射波声场重构的误差ε,将会明显减小。
2.3 入射波声场重构的实验验证
在实验中,使用刚性表面球形传声器阵列测量总声压,运用球面近场声全息方法,重构球形阵列表面及外部空间区域的入射波声场。实验布置如图6所示,刚性表面球形传声器阵列上,各传声器处的声压,通过B&K-LANXI设备采集,并通过PULSE软件进行FFT处理得到声压频域数据,进而可进一步进行声场重构的计算。实验在全消声室内进行,球形阵列的球心设为坐标系中心;在球形阵列外部空间,布置一个扬声器作为声源,扬声器与功放设备控制模块相连接,发出指定频率的声音。

图6 实验布置照片
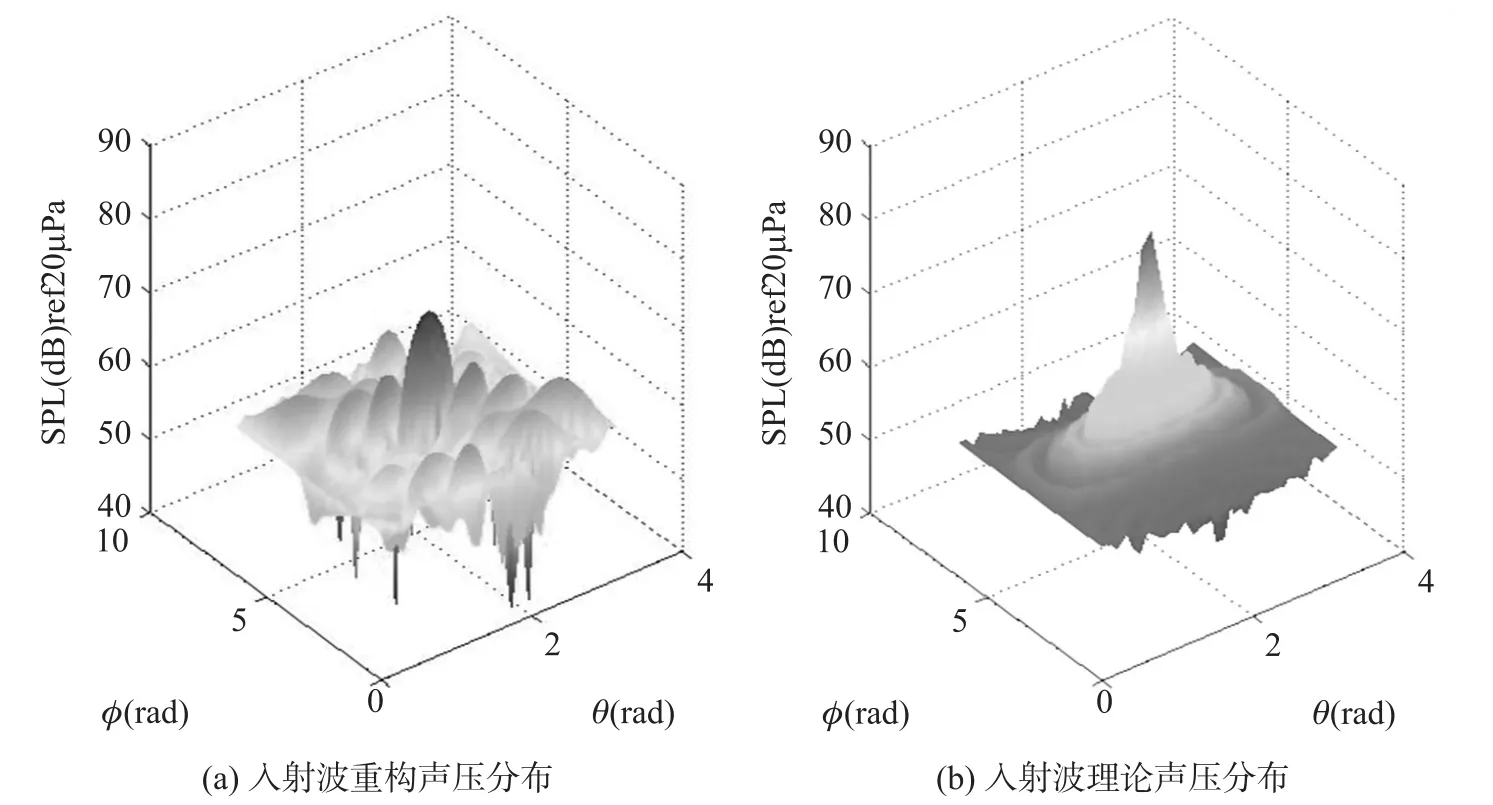
图5 声源所在球面处声场声压重构值与理论值比较(a=0.2 m,k=15,M=64,R=0.5 m,SNR=40 dB)
2.3.1 实验I
在本实验中,使用一个刚性表面球形传声器阵列作为测量前端,球形阵列的半径a为0.15 m,阵列上传声器的数目M为64。按照上述实验设置,将扬声器放置在距离阵列中心0.2 m处,声源频率f为800 Hz,即波数k为14.8,使用球形阵列测量声场总声压,然后重构球形阵列表面入射波声压分布,如图7所示。
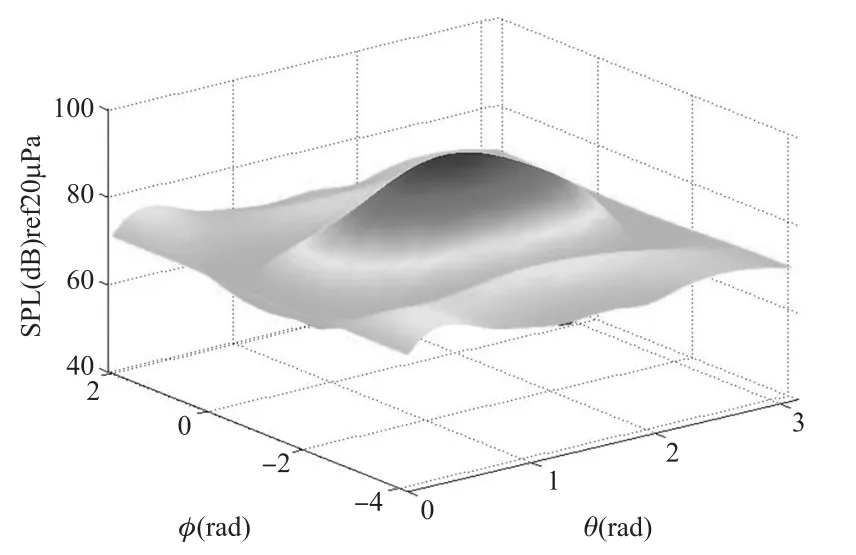
图7 波数k为14.8时,由球面近场声全息方法重构出的球形阵列表面处入射波声压分布(阵列半径a=0.15 m,声源离阵列中心距离d=0.2 m,传声器数目M=64)
将各传声器位置处重构声压与各传声器所测得声压进行比较,结果如图8所示,由公式(12)可得它们之间的偏差达20.2%,说明声场分布在经过刚性球面散射后变化很大,因而分析由刚性球面引起的声波散射现象,对由刚性表面球形传声器阵列重构入射波声场的研究有着重要意义。

图8 各传声器位置处声压的测量值与入射波声压重构值比较(阵列半径a=0.15 m,声源离阵列中心距离d=0.2 m,传声器数目M=64,波数k=14.8)
将重构面半径设定为R=0.2 m,根据传声器测量的总声压,运用球面近场声全息方法,可得出声源所在球面处的入射波声压分布,如图9所示,通过此声压分布图可以明显得出,声源的方位为(1.5 rad,-1.1 rad)。
2.3.2 实验II
在本实验中,使用一个B&K公司的刚性表面球形传声器阵列[15]作为测量前端,阵列的半径a为0.097 5 m,阵列上传声器的数目M为36。按照实验I的布置,作为声源的扬声器放置于(0.13 m,1.6 rad,4.7 rad)处。在刚性表面球形阵列外部空间中,放置一个1/4英寸检验传声器,位于(0.107 5 m,1.6 rad,5.2 rad)处,其方位对应于球形阵列表面处编号为7的传声器,两者相距1 cm,用于检验入射波声场重构的精度。
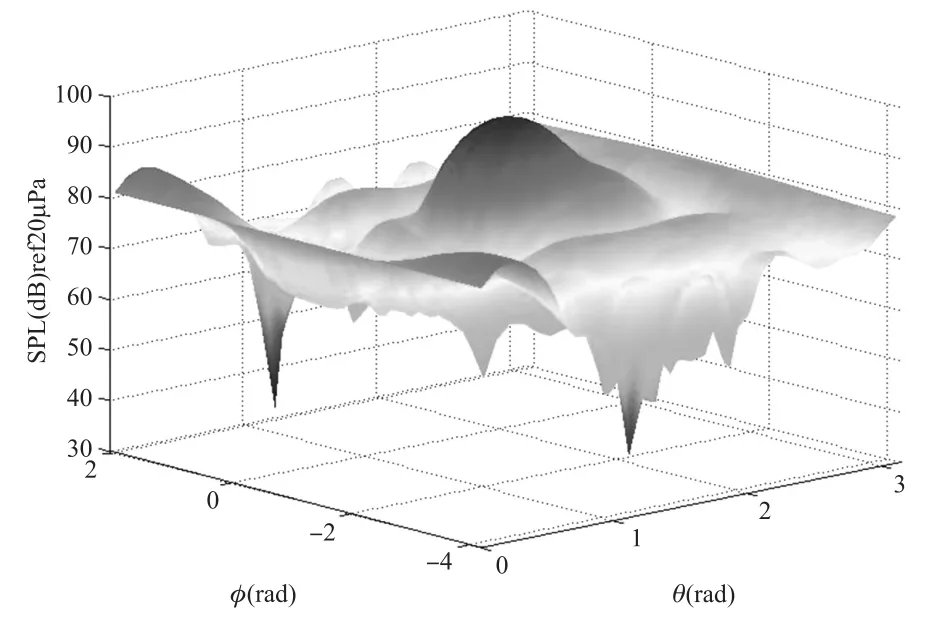
图9 球面近场声全息方法重构出的声源所在球面处入射波声压分布(阵列半径a=0.15 m,声源离阵列中心距离d=0.2 m,传声器数目M=64,波数k=14.8)
实验步骤如下:首先分别设置声源频率f为200 Hz、500 Hz、800 Hz、1 500 Hz、2 500 Hz、4 000 Hz,由球形阵列与声场中传声器进行声压信号测量。然后,将球形阵列移开,则声场中只有声源与检验传声器,保持它们的位置不变,再次分别在声源频率f为200 Hz、500 Hz、800 Hz、1 500 Hz、2 500 Hz、4 000 Hz的情形下,由此检验传声器测量入射波声场的声压信号。由实验步骤可知,前一次球形阵列与检验传声器,测量的信号为总声压值,而后一次检验传声器的测量值为入射波声场的声压值。根据第2节介绍的入射声场重构理论,可采用前一次球形阵列测量到的总声压值,重构出检验传声器位置的入射波声场声压值,并与检验传声器直接测量的入射波声场声压减小对比,以检验其声场重构的计算精度。在上述各实验频率下,在检验传声器位置处,直接测量总声压值、直接测量入射波声场声压值以及运用近场声全息方法重构得出的入射波声场声压值,如图10所示。
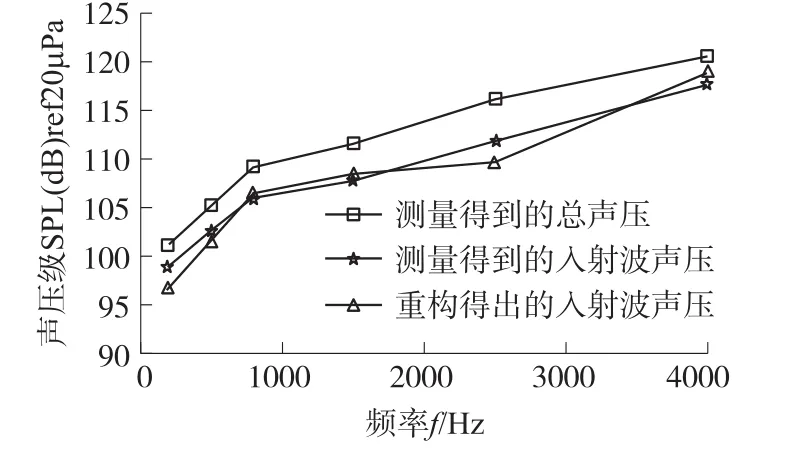
图10 各频率下,检验传声器位置处总声压、入射波声场声压和重构的入射波声场声压的比较(阵列半径a=0.097 5 m,声源离阵列中心距离d=0.13 m,传声器数目M=36)
由图10可得,对于检验传声器位置处,总声压测量值与入射波声场声压测量值均随着频率f的增大而增大,在各频率下总声压测量值大于入射波声场声压测量值,这符合第1.2节中的分析,因为检验传声器位于声源与阵列之间的声场区域。由于检验传声器位置处的总声压测量值与入射波声场声压测量值分别为两个实验步骤下对应的测量值,因而两者只能在幅值大小上进行比较,实验结果为,在检验传声器位置处,各频率下散射后的总声压级较散射前的入射波声场声压级要大约4 dB左右,这说明声源辐射的声场在经过球形阵列散射后发生了较大的变化。同时,由图10可得,在各频率下,对于检验传声器位置处,声场重构得出的入射波声场声压级及与测量的入射波声场声压级很接近,误差在2 dB以内,这说明运用基于散射声场模型的近场声全息方法,可以以一定的精度重构出入射波声场。其中,此误差不仅仅是声场重构计算方法引起的,其它影响误差的因素主要有传声器测量误差以及检验传声器坐标误差等。
上述两组实验表明,采用刚性表面球形传声器阵列测得的总声压,基于考虑声场散射的声场模型和球面近场声全息方法,可以重构出入射波声场,消除由于球形阵列刚性表面散射造成的计算入射波声场的误差。
3 结论
本文通过应用刚性球体表面的声波散射的数学模型,建立起声场入射波声压与发生散射后总声压之间的关系。针对不同的波数,检验了球面波遇到刚性表面球体发生散射后,球体表面及外部空间声场声压分布的变化规律。通过仿真与实验检验了由刚性表面球形阵列上传声器测得的总声压,运用球面近场声全息方法,在球形阵列表面及外部空间中入射波声场重构的精度。得出如下结论:①刚性球体表面处声压分布在散射前与散射后发生了较大的变化,因而在入射波声场重构时,需要在声场建模中考虑刚性球面的声波散射。②通过建立刚性球面对声波散射的数学模型,并应用于球面近场声全息方法中,可由刚性表面球形传声器阵列测量的总声压,实现入射波声场的重构。在入射波声场重构中,重构误差会随着重构半径的增大而增大,在球形阵列外部的较近区域,能取得较高的重构精度。同时,在波数较大时,由于声源近场信息衰减较快,重构误差随重构半径增大而急剧增大;而在波数较小时,重构误差随重构半径增大则较缓慢地增大,即使在重构半径较大的情形下,重构误差也相对较小。此外,当重构面为声源所在球面时,即使在总的重构误差较大的情形下,通过重构出的入射波声压分布图,依然可以很好地识别出声源的方位。
本文研究在多个方面还需要进一步研究:①本文以完全刚性球体的边界条件,得出了声波散射的声场数学模型。但在实际中,刚性表面球形传声器阵列的球面上镶嵌有多个传声器,在传声器位置波动方程解并不满足刚性面散射的Neumann边界条件。为提高入射波声场的重构精度,需要考虑建立更精确的刚性表面球形传声器阵列的散射边界条件模型。②在入射波声场的重构中,由测量误差或环境噪声引起的微小误差会在声场重构逆向变换的过程中放大。引入如Tikhonov法或Landweber迭代法等正则化方法,可进一步提高入射波声场的重构精度,由于论文篇幅的限制,本文没有进行探讨。
[1]Williams E G,Nicolas Valdivia,Peter C Herdic,et al.Volumetric Acoustic Vector Intensity Imager[J].Journal of the Acoustical So⁃ciety of America,2006,120:1887-1897.
[2]Jacobsen F,Moreno G,Grande E F,et al.Near Field Acoustic Ho⁃lography with Microphones Mounted on a Rigid Sphere[C]//Pro⁃ceedings of Inter-Noise.2008.
[3]Williams E G,Takashima K.Vector Intensity Reconstructions in a Volume Surrounding a Rigid Spherical Microphone Array[J].Jour⁃nal of the Acoustical Society of America,2010,127(2):773-783.
[4]Jacobsen F,Moreno G,Grande E F,et al.Near Field Acoustic Ho⁃lography with Microphones on a Rigid Sphere[J].Journal of the Acoustical Society of America,2011,129(6):3461-3464.
[5]Lu H,Li M.Reconstruction of Sound Field Based on Near-Field Acoustic Holography with a Rigid Spherical Microphone Array[C]//Proceedings of the Hong Kong:ACOUSTIC 2012 Hong Kong Conference and Exhibition.2012:3258-3258.
[6]Hardin R H,Sloane N J A.McLaren’s Improved Snub Cube and other New Spherical Designs in Three Dimensions[J].Discrete Computational Geometry,1995(15):429-441.
[7]莫尔斯P M,英格德U.理论声学[M].杨训仁,吕如榆,译.北京:科学出版社,1984.
[8]杜功焕,朱哲民,龚秀芬.声学基础[M].第3版.南京:南京大学出版社,2012.
[9]张海澜.理论声学[M].北京:高等教育出版社,2007.
[10]褚志刚,杨洋,蒋忠翰.波束形成传声器阵列性能研究[J].传感技术学报,2011,24(5):665-670.
[11]丁浩,李春晓,金江明,等.可识别声源深度的三维声聚焦波束形成方法[J].传感技术学报,2013,26(2):175-181.
[12]刘梦然,张国军,简泽明,等.管道内检测器声定位技术研究[J].传感技术学报,2014,27(4):500-504.
[13]Franz Zotter.Analysis and Synthesis of Sound-Radiation with Spherical Arrays[D].Austria:Institute of Electronic Music and Acoustics University,2009.
[14]Lu Huancai.Reconstruction of Vibroacoustic Responses Using Helmholtz Equation Least-Squares Method[D].Doctoral Disserta⁃tion,Detroit:Wayne State University,2007.
[15]Haddad K,Hald J.3D Localization of Acoustic Sources with a Spherical Array[J].Journal of the Acoustical Society of America,2008,123(5):3311-3311.

李敏宗(1988-),男,浙江工业大学博士研究生,主要研究方向为噪声源识别定位及传声器阵列信号处理,limin⁃zong_svlab@163.com;

卢奂采(1962-),女,教授,博导,美国声学学会会员,美国机械工程师学会会员,2007年于美国Wayne State Universi⁃ty获得机械工程博士学位,1996年于浙江大学获得工学博士学位,主要从事3D传声器阵列理论、声全息理论及声场可视化和声学图像处理等方面的研究,huancailu@zjut.edu.cn。
Reconstruction of Incident Sound Field and Identification of Sound Source Using a Rigid Spherical Microphone Array*
LI Minzong1,LU Huancai1,2*,JIN Jiangming1
(1.Key Laboratory of Equipment&Manufacturing,Ministry of Education&Zhejiang Province,College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou 310014,China;2.Zhejiang Key Laboratory for Signal Processing,Zhejiang University of Technology,Hangzhou 310014,China)
Rigid spherical microphone array is an ideal measurement front-end for three-dimensional sound field re⁃construction.However,as the rigid surface of the array scatters incident sound waves,the directly measured pres⁃sures and near-field acoustic holography approach based on the math model of free field could not be employed to reconstruct the incident sound field.In this paper,the math model of scattered sound field based on Neumann boundary condition was applied;the relationship between the total sound pressure after scattering and the incident sound pressure was developed and analyzed.Then the incident sound field was reconstructed by using the input da⁃ta of measured total sound pressure with a rigid microphone array.The variation of sound pressure distribution on the surface of rigid sphere was examined through simulations and experiments.And the reconstruction accuracy was examined when the reconstruction parameters,such as frequency and reconstruction radius,varied.The reconstruc⁃tion results show that the incident sound field can be reconstructed with certain accuracy with a rigid spherical mi⁃crophone array,based on spherical near-field acoustic holography with the math model of scattered sound field.
spherical microphone array;reconstruction of incident sound field;spherical near-field acoustic holog⁃raphy;sound wave scattering;rigid surface sphere
TB877.2
A
1004-1699(2015)10-1459-08
��7320Q;7810
10.3969/j.issn.1004-1699.2015.10.007
项目来源:国家自然科学基金项目(51205354,51275469);浙江省国际科技合作专项项目(2013C14014)
2015-03-12 修改日期:2015-08-12

