考虑不可再造率的闭环供应链模糊契约设计

高文军，陈菊红

（1.山西师范大学 经济与管理学院，山西 临汾041000； 2.西安理工大学 经济与管理学院，陕西 西安710054）

再制造闭环供应链是将利用新鲜原材料进行生产的生产方式与利用回收的废旧产品进行再造生产的生产方式有效整合的一种供应链管理模式，它不仅能有效节约资源和保护环境，还能增加企业绿色声誉和经济利润，因而成为学术界关注的热点问题之一。在再制造闭环供应链的优化与协调研究中，一个关键的环节是如何刻画不可再制造率。当前已有研究为简单起见，往往假定不可再制造率为零，即所有回收的废旧产品均可完全用于再造生产。在此假设下，Savaskan et al.［1］研究了废旧产品回收商的选择对供应链企业决策及利润的影响；黄祖庆等［2］对不同主导决策模式下的第三方回收闭环供应链的决策效率进行了比较研究；Savaskan R C et al.［3］在竞争环境下分析了产品批发价格、零售价格与废旧产品回收价格之间的关系；Shen-Lian Chung et al.［4］基于库存模型设计了能激励节点企业从供应链系统最优视角决策的契约；陈菊红等［5］构建了能协调第三方回收闭环供应链的收入-费用共享契约；聂佳佳等［6］则研究了零售商市场预测信息分享情况对供应链节点企业决策的影响；Zheng Yingfei et al.［7］利用改进的夏普里值法研究了闭环供应链的收益分配问题；Jie Li［8］则分析了零售商的主导地位对闭环供应链决策的影响。此外，也有少数学者基于闭环供应链存在较大不确定性的认识而利用模糊理论对相关问题进行了研究。如赵静等［9］基于模糊理论分析了闭环供应链的分散、集中与协调决策问题；周岩等［10］与桑圣举［11］在模糊市场需求下分别对双渠道闭环供应链的网络均衡和优化协调问题进行了研究；魏杰等［12］对模糊环境下闭环供应链节点企业间的博弈定价决策问题进行了分析；张松涛等［13］则对网络环境下考虑成本切换的闭环供应链的离散动态模型和模糊鲁棒控制问题进行了研究。

类似相关研究丰富了闭环供应链的优化与协调理论，但文中回收废旧产品全部可用于再造生产的假设与现实显然不符。现实中诸如废旧产品本身质量问题及拆解技术问题等的不确定性常常导致部分废旧产品只能进行物料资源再利用和再循环，而不能用于再制造，因而不可再造率非但不为零，而且还具有很大的不确定性，甚至都难以给出一个概率分布，而只能对其可能变动情况做出一个较为模糊的估算。不可再造率的模糊特性会影响再制造闭环供应链及节点企业的最优决策和系统协调，因此本文拟在视不可再造率为模糊数的前提下，利用梯形模糊数与博弈理论研究再制造闭环供应链的优化与协调问题，以期望为闭环供应链管理实践提供参考和借鉴。

二、问题的描述与研究假设

本文研究由单个零售商和制造商组成的两阶再制造闭环供应链的模糊优化问题。制造商生产单一的短生命周期产品，cm表示利用新鲜原材料进行生产时的单位生产成本，crm表示利用回收的废旧产品进行再制造生产时的单位再造成本，w为产品批发价格，p为产品零售价格，q为零售商的订货量，v为销售季节过后剩余产品的清空价格，b2为零售商面向消费者的单位废旧品回收价格，b1为制造商面向零售商的单位废旧品转移价格［14］。X表示随机市场需求，其密度函数与概率分布函数分别为f(x)和F(x)。L为废旧产品回收量，L=k+hb2，θ( 0＜θ＜1) 为不可再造率，θ～ 为模糊化的不可再造率。假设不考虑消费者的产品退货以及制造商和零售商的库存与缺货成本。

此外，本文的模糊运算将依据函数原理与梯形模糊数进行，解模糊将采用文献［15-16］提出的梯级平均积分法进行。即若e(0＜e) ≤1 为任意水平的隶属度，则对于梯形模糊数=(a1,a2,a3,a4)LR，其解模糊值可表示为：

三、模型的构建

由问题描述与假设可知，当零售商的订货量为q时，其期望销售量s(q)与库存量I(q)分别为：

其中，F¯(x)=1-F(x)，E表示求数学期望，符号“^”表示两者取小，(q-x)+表示q-x与0取大。

（一）未考虑不可再造率的收益共享-费用共担契约

假设μ( 0＜μ＜1) 为制造商与零售商均能接受的收益分享与费用分担比例，则未考虑不可再造率时闭环供应链系统与零售商的利润函数分别为：

（二）考虑不可再造率的收益共享-费用共担契约

假设对于零售商的销售收益和回收成本零售商以比例φ(0＜φ＜1)进行分享和分担。对于制造商的不可再造回收成本，由于零售商不具备相关专业知识，因而在回收时无法对废旧产品的再造特质进行甄别，再者废旧产品不可再造也可能是由于制造商的拆解技术等原因造成的，因此本文假设此部分成本完全由制造商承担。基于以上假设可知考虑不可再制造率时闭环供应链系统与零售商的利润函数分别为：

四、模型求解

（一）标准收益共享-费用共担契约

证明：将w=μcm与b1=μΔ代入式（2），则零售商的利润函数可以写为：

即零售商的利润函数可以表示为闭环供应链系统利润函数常数项为零的线性函数，因此使零售商利润最大的订货决策和回收价格决策亦是使供应链系统利润最大的订货决策和回收价格决策。这说明：在μ满足制造商与零售商的参与约束时，标准的收益共享-费用共担契约能协调不考虑不可再造率的闭环供应链。

（二）模糊收益共享-费用共担契约

当考虑不可再造率，同时将不可再造率θ和契约参数φ模糊化时（模糊不可再造率导致模糊契约参数），比较式（3）和（4）可得定理2。

定理2的证明过程与定理1类似，此处省略。

综上所述，模糊收益共享-费用共担契约同样能够使拥有模糊不可再造率的闭环供应链实现协调。现在面临的问题是对w～ 与进行模糊运算和模糊求解。假设不可再造率θ和契约参数φ分别为梯形模糊数

将式（5）与（6）代入w～ 与b～1，运用函数原理进行模糊运算后可得：

运用梯级平均积分对式（7）和（8）两个梯形模糊参数进行模糊求解得：

依上所述，根据给出的模糊不可再造率及模糊契约参数的具体梯形模糊数便可得到一个模糊收益共享- 费用共担契约的协调参数组。显然在不可再造率模糊情况下，给出一个梯形模糊数要比给出某个具体的参数值更为方便和容易，这也体现了模糊收益共享-费用共担契约的柔性和灵活性。

（三）讨论

当φ1=φ2=φ3=φ4=μ，θ1=θ2=θ3=θ4=0 时，模糊收益共享-费用共担契约转化为标准的收益共享-费用共担契约； 当φ1=φ2=φ3=φ4=μ，θ1=θ2=θ3=θ4=θ时，模糊收益共享-费用共担契约退化为考虑不可再造率的收益共享-费用共担契约。这说明标准收益共享-费用共担契约和考虑不可再造率的收益共享-费用共担契约都是模糊收益共享-费用共担契约的特例。

五、数值算例

考虑由一个产品制造商与一个零售商组成的再制造闭环供应链。假定市场需求D服从均匀分布（110，1110）。回收废旧产品的不可再造率约为0.06，契约参数φ约为0.6。按照“y≈(0.89y,0.94y,1.06y,1.11y)”的转换方式可将模糊不可再造率θ～ 和模糊收益共享-费用共担契约参数φ～ 转换为以下具体的梯形模糊数：

其他再制造闭环供应链基本参数的取值具体如表1所示。

表1 再制造闭环供应链基本参数取值

由表2 可知：①在考虑不可再造率情况下，废旧产品的转移价格、回收价格、零售商及制造商的利润均随着不可再造率的增大而减小。这是由于随着不可再造率的增加，制造商为了维护自身再制造活动经济利益所采取的降低转移价格的策略致使零售商采取了降低其废旧品回收价格策略，而这又导致了废旧品回收量的降低，进而减少了零售商与制造商在逆向供应链渠道的利润。②制造商的产品批发价格和零售商的订货量与不可再造率无关。这表明不可再造率不影响传统前向供应链的利润。

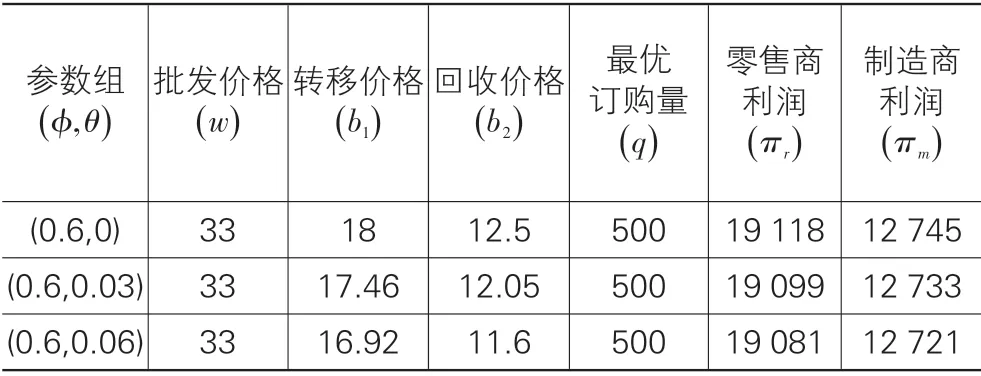
表2 不同契约参数的比较

由此可得以下管理启示：制造商与零售商应当采取有效合作措施降低废旧产品的不可再造率，从而减少不可再制造率对供应链节点企业及整个系统收益的负面影响。

表3表明：考虑不可再造率的模糊收益共享-费用共担契约与考虑确定性不可再造率的收益共享-费用共担契约具有相同的协调功能，这表明模糊收益共享-费用共担契约在再制造闭环供应链管理实践中是可行性的，因为给出一个不可再造率的梯形模糊远比给出一个精确的不可再造率更加容易和方便。

表3 模糊与非模糊状态下不同契约参数的比较

此结论的管理启示为：当制造商与零售商对废旧产品不可再造率和分享比例系统存在异议时，构建模糊收益共享-费用共担契约是一个很好选择。

六、结束语

针对现实中回收的废旧产品通常存在不可再造的情形，本文利用模糊数学理论分析了废旧产品不可再造率对闭环供应链协调决策及利润的影响，将不可再造率和收益共享-费用共担比例系数假定为梯形模糊数，设计了一种考虑不可再造率且能协调供应链的模糊收益共享-费用共担契约，并运用模糊运算法则对模糊协调参数进行了模糊求解。研究显示：不可再造率对闭环供应链契约参数的影响程度不同，对废旧产品转移价格、回收价格及节点企业利润存在消极影响，而对产品批发价格和订货量则不存在影响；不可再造率仅对逆向供应链渠道利润产生影响，而对传统前向供应链渠道利润没有影响；模糊收益共享-费用共担契约是优化与协调再制造闭环供应链系统的一种有效方法。

本文在构建模糊收益共享-费用共担契约时没有考虑不可再造废旧产品的残值，未来可在虑及残值的基础上对闭环供应链的协调问题进行细化研究。

［1］Savaskan R C，Bhattacharya S，Van Wassenhove L N.Closed-loop supply chain models with product remanufacturing［J］. Management Science，2004，50（2）：239-252.

［2］黄祖庆，易荣华，达庆利. 第三方负责回收的再制造闭环供应链决策结构的效率分析［J］. 中国管理科学，2008，16（3）：73-77.

［3］Savaskan R C，Wassenhove L N V. Reverse channel design:the case of competing retailers［J］. Management Science，2006，52（1）：1-14.

［4］Shen-Lian Chung，Hui-Ming Wee，Po-Chung Yang. Optimal policy for a closed-loop supply chain inventory system with remanufacturing［J］. Mathematical and Computer Modeling，2008，48（5/6）：867-881.

［5］陈菊红，史成东，郭福利. 第三方负责回收再制造闭环供应链契约设计［J］. 工业工程与管理，2010，15（2）：17-21.

［6］聂佳佳，熊中楷. 信息分享模式对第三方负责回收闭环供应链的影响［J］. 管理工程学报，2011，25（2）：74-81.

［7］Zheng Yingfei，Zhang Shuxia，Chen Xiaojing，et al. Application of Modified Shapley Value in Gains Allocation of Closed-loop Supply Chain under Third-Party Reclaim［J］.Energy Procedia，2011（5）：980-984.

［8］Jie Li. Retailer-driven closed-loop supply chains with product remanufacturing［D］. Ames：Iowa State University，2006.

［9］赵静，魏杰，孙晓晨. 基于模糊理论的闭环供应链定价决策研究［J］. 模糊系统与数学，2010，24（6）：76-84.

［10］周岩，胡劲松，孙浩，张桂涛. 具有模糊需求的双渠道闭环供应链网络均衡［J］. 中国管理科学，2012，20（专辑）：481-490.

［11］桑圣举. 模糊需求下的闭环供应链协调机制研究［J］. 计算机工程与应用，2012，48（17）：36-40.

［12］魏杰，赵静，李勇建. 模糊环境下基于再制造闭环供应链的博弈问题研究［J］. 系统科学与数学，2011（11）：1564-1577.

［13］张松涛，赵晓伟. 基于成本切换的闭环供应链离散动态模型及其模糊鲁棒控制［J］. 计算机集成制造，2013，19（6）：1385-1396.

［14］高文军，陈菊红. 基于CVaR 的闭环供应链优化与协调决策研究［J］. 控制与决策，2011，26（4）：489-494，500.

［15］Chen S H，Chang S M. Optimization of fuzzy production inventory model with unrepairable defective products［J］. International Journal of Production Economics，2008，113（2）：887-894.

［16］刘海军，陈菊红. 基于不可修复缺陷情境下的供应链模糊回购契约［J］. 控制与决策，2010，25（8）：1155-1158，1163.