一种基于改进人工蜂群算法的机器人实时路径规划方法

殷霞红，倪建军，吴榴迎

(河海大学物联网工程学院，江苏 常州 213022)

0 引言

在移动机器人自主导航中，路径规划是核心研究问题之一。所谓机器人路径规划，就是在有障碍物的环境下，根据一些准则为机器人找到一条从起始位置到目标位置的最优无碰撞的路径［1］。机器人路径规划的研究始于20 世纪70 年代，总的来说，路径规划方法可以分成2 种:经典方法和启发式方法。经典的路径规划方法主要包括:势场法［2］、网格法和可视图法［3］。

势场方法拥有简单的结构，但是这种方法有一些固有的局限性，包括容易陷入局部最小值，在邻近障碍物之间找不到通道等［2］。在网格法中，存在的主要问题是如何确定网格的大小。可视图法的缺点是搜索效率较低。

由于经典方法存在许多不足，学者们开始研究基于启发式方法的机器人路径规划，主要包括模糊逻辑、神经网络、遗传算法等［4-6］，并取得了不少成果。近年来，越来越多的群体智能算法开始应用于路径规划，例如蚁群算法、粒子群算法、蛙跳算法等［7-9］。这些群体智能算法也有一定的局限性，例如容易陷入局部最优等。针对这些问题，研究人员提出了一些改进方法，如康冰等人［10］提出了一种改进的蚁群算法，通过采用折返蚂蚁等策略，提高了算法的收敛速度和机器人搜索最优路径的能力。Shakiba 等人［11］使用费格森样条函数和粒子群算法完成仿人足球机器人的路径规划。

人工蜂群算法［12］是由Karaboga 于2005 年提出来的一种新型仿生群体智能算法，由于其搜索速度快、参数少、易于实现等优点，已经成功应用于求解TSP 问题［13］、任务调度、图像处理［14］等许多领域。近年来，人工蜂群算法被尝试用于求解路径规划问题，但是传统的人工蜂群算法存在容易陷入局部最优，且搜索效率低下等不足。针对这些问题，本文提出一种基于改进人工蜂群算法的路径规划方法，并进行了仿真实验，仿真结果证明了该方法的可行性与有效性。

1 基于改进人工蜂群算法的机器人路径规划方法

机器人路径规划包括如下几个方面的问题需要解决，一是环境建模问题，另一方面是对路径的评价问题。本文采用一种改进人工蜂群算法实现机器人路径规划，具体介绍如下。

1.1 环境建模

采用栅格法建立移动机器人的环境模型，首先作如下假设:1)机器人工作在二维环境中，机器人的起始位置和终点位置已知，且忽略环境中障碍物的高度信息;2)假设机器人为一个质点，忽略机器人的实际尺寸;3)环境中障碍物所在的栅格用黑色表示，没有障碍物的栅格用白色表示，机器人可以在白色栅格中进行运动。在此基础上，建立环境栅格模型:假设机器人的移动步长为R(一般设R=1)，以R 为单位对直角坐标系的横轴和纵轴进行划分，从而将整个环境划分为栅格地图，则每行的栅格数为;每列的栅格数为。栅格的位置可以由坐标或者序列号表示，图1 表示坐标与序列号之间的关系。

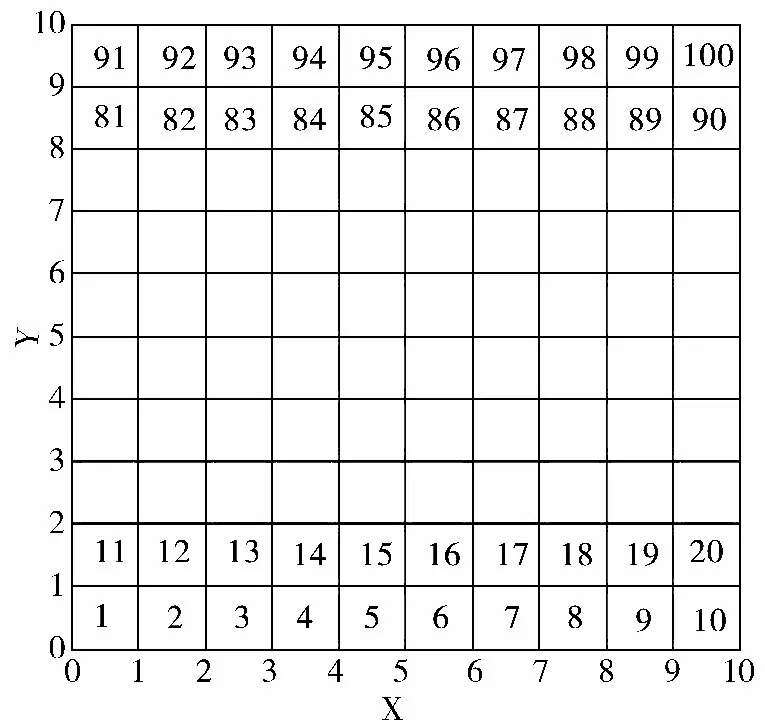
图1 栅格序列号与坐标关系示意图

1.2 适应度函数

机器人路径规划的目标是找到一条尽可能短的路径，且要避开障碍物，因此，设计适应度函数如下:

其中，k 是权值，这里取k=0.5，Dn表示路径长度的代价，Pn表示与障碍物碰撞的代价。设机器人的路径由D 个路径节点构成，则Dn和Pn的计算如下:

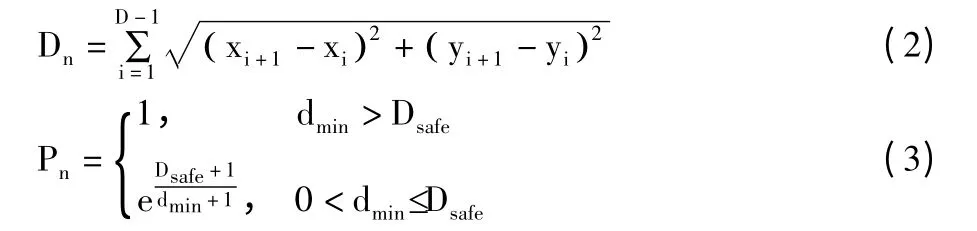
公式(3)中，Dsafe表示机器人的安全距离，dmin为路径到障碍物的最短距离。fitness 的值越小，对应的解越优，即规划出来的路径越短。

1.3 基于改进人工蜂群算法的路径规划

由于蜜蜂寻找最优食物源的过程和路径规划很相似，所以人工蜂群算法很适合用于解决机器人路径规划问题。在人工蜂群算法中，蜜蜂分为3 种角色:引领蜂、跟随蜂和侦察蜂，基于人工蜂群的路径规划方法如下:

首先，随机生成N 个可行解(X1，X2，…，XN)作为初始路径，每条路径Xi可表示为Xi=(xi1，xi2，…，xiD)，其中Xi中的每个元素对应于环境模型中的栅格序列号，D 为路径节点数。然后，引领蜂对初始路径进行一次邻域搜索，如果新搜索到的路径的适应度函数值优于之前的路径，则用新路径替换旧路径，否则保持原路径不变。当全部引领蜂完成搜索后，回到蜂巢把路径的信息传达给跟随蜂，跟随蜂通过精英保留选择策略进行路径选择，一旦选中后，也进行一次邻域搜索，并保留较优的解，人工蜂群算法就是通过不断重复搜索，最终找到最优的解［15］。

引领蜂和跟随蜂通过自适应的搜索方式对路径位置进行更新，本文采用的更新公式如下:

传统的人工蜂群算法中，跟随蜂是通过轮盘赌选择路径的，很有可能具有高适应度值的路径通过轮盘赌而被忽略了。为了解决这个问题，提高算法的性能，本文采用基于精英保留的选择策略，即让最好的路径不需要通过轮盘赌机制而直接进入下一个步骤，防止较短路径被遗漏。

在本文改进的人工蜂群算法中，利用参数Times记录某条路径被更新的次数，如果某条路径连续循环的次数Times 达到一定阈值ε，却没有得到改善，表示这条路径陷入局部最优，则舍弃该路径，重新随机产生一条新的路径代替原来的路径进入循环。

基于改进人工蜂群算法的路径规划方法的基本步骤归纳如下:

1)初始化参数。主要包括可行路径的数目N，路径节点数D，最大迭代次数Gmax，最大限制次数ε。

2)将机器人的运动环境根据栅格法进行建模，并在该环境下，随机生成N 条可行路径。

3)每只引领蜂按照公式(4)对初始路径进行邻域搜索，如果新产生的路径的适应度函数值优于当前的，则替代当前路径，否则保持不变。

4)跟随蜂按照精英保留选择策略，把最好的路径选择出来直接进行搜索，然后其余的跟随蜂按照轮盘赌机制选择一条路径进行搜索，记录较优解。

5)如果某条路径循环ε 次后，仍得不到更新，则在解空间中，重新初始化一条路径取代它。

6)如果搜索次数达到Gmax，则记录最优路径，并跳转到步骤7)，否则跳转到步骤3)开始重新搜索。

7)将路径中的各个节点连接起来，就得到机器人的规划路径。

2 仿真实验和结果分析

图2 初始环境图

为了验证基于改进人工蜂群算法的机器人路径规划方法的准确性与可行性，本文在Intel Core2 CPU，2.1 GHz，Matlab 环境下进行了仿真实验。将机器人运动环境划分成15 ×15 个栅格，人工蜂群算法中，参数设置为:路径数目N=10，路径节点数D=10，最大迭代次数Gmax=200，ε=5，Dsafe=1。机器人和目标分别由一个小圆和三角形表示，初始环境图如图2 所示，黑色部分表示障碍物。在相同参数设置下，用传统的人工蜂群算法(ABC)和本文改进的人工蜂群算法(IABC)进行对比实验。2 种算法分别进行10 次实验，其中一次的仿真实验结果如图3 所示，相关数据见表1 所示。图4 给出了2 种算法的进化曲线，其中横坐标为迭代次数，纵坐标为路径长度值。

表1 2 种算法下的实验结果

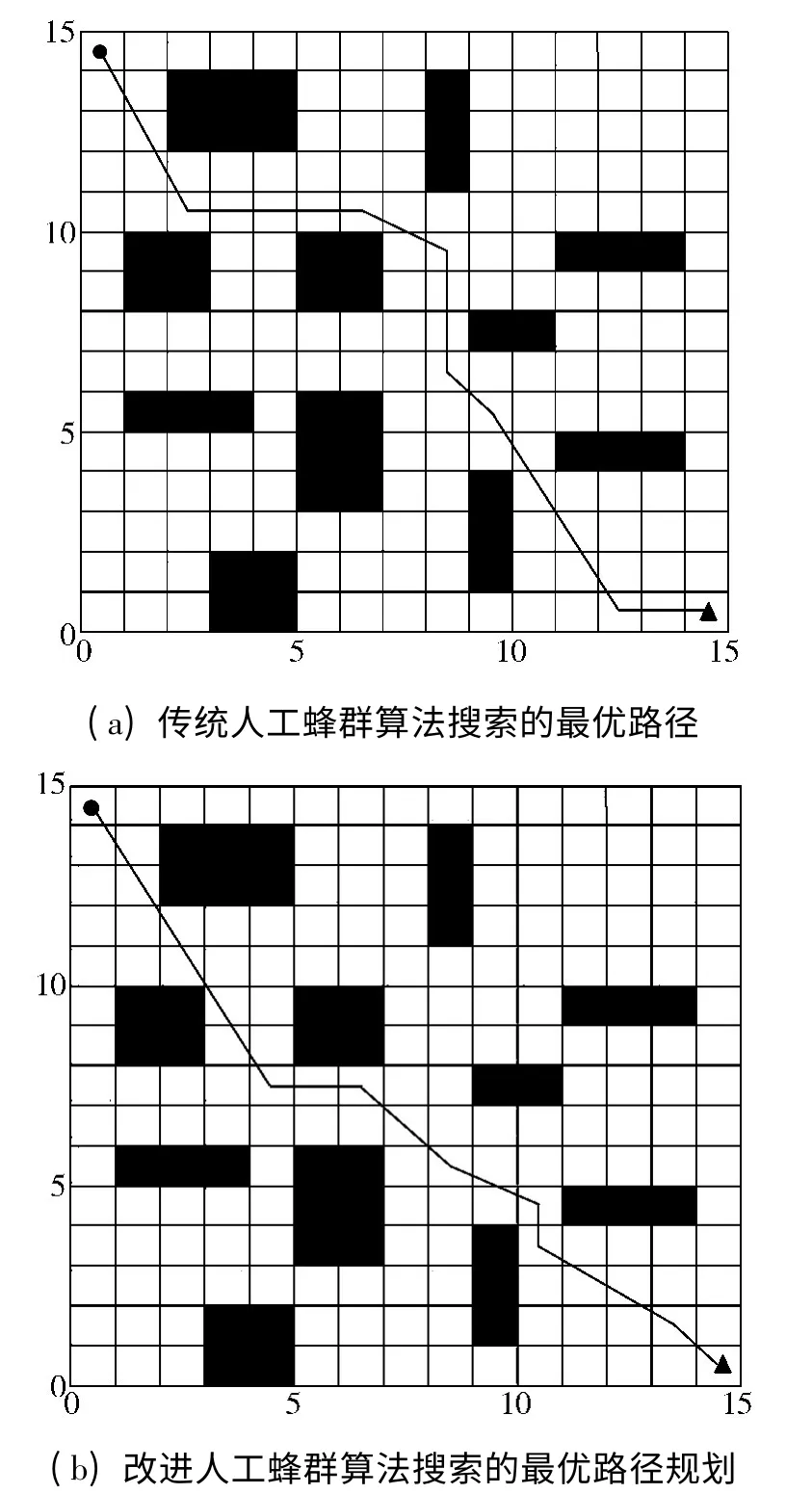
图3 仿真结果图

图4 2 种算法下的进化曲线图

由表1 中的数据和图3 的路径规划曲线可以看出，改进算法所得到的路径长度优于传统算法，且10次实验的方差也远小于传统的人工蜂群算法，说明本文改进算法的稳定性较好。除此之外，本文算法的运行时间也大大缩短了，有利于提高机器人运行的效率。从图4 中可以看出，本文算法当迭代次数达到45 次左右以后，就能找到最优路径，而传统的人工蜂群算法要到120 次左右才能发现最优路径，可见本文算法具有更好的寻优能力以及更好的全局收敛速度。

3 结束语

本文提出了一种改进的人工蜂群算法用来解决机器人路径规划问题;提出了一种自适应的搜索方式来提高算法的收敛速度，并且采用基于精英保留的选择策略避免路径陷入局部最优;最后，通过仿真实验验证了本文改进的算法比传统人工蜂群算法更有效。本文提出的路径规划方法在移动机器人控制领域具有广泛的应用，例如，危险环境下的机器人搜捕和火灾探测等［16-17］。

［1］马千知，雷秀娟.改进粒子群算法在机器人路径规划中的应用［J］.计算机工程与应用，2011，47(25):241-244.

［2］石为人，黄兴华，周伟.基于改进人工势场法的移动机器人路径规划［J］.计算机应用，2010，30(8):2021-2023.

［3］杨淮清，肖兴贵，姚栋.一种基于可视图法的机器人全局路径规划算法［J］.沈阳工业大学学报，2009，31(2):225-229.

［4］陈卫东，朱奇光.基于模糊算法的移动机器人路径规划［J］.电子学报，2011，39(4):971-974.

［5］Li H，Yang S X，Seto M L.Neural-network-based path planning for a multirobot system with moving obstacles［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part C:Applications and Reviews，2009，39(4):410-419.

［6］Tsai C C，Huang H C，Chan C K.Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation［J］.IEEE Transactions on Industrial Electronics，2011，58(10):4813-4821.

［7］刘广瑞，刘军，孔令云.移动机器人路径规划蚁群算法及其收敛性分析［J］.郑州大学学报(工学版)，2012，33(2):24-27.

［8］靳其兵，赵振兴，苏晓静，等.基于粒子健康度的快速收敛粒子群优化算法［J］.化工学报，2011，62(8):2328-2333.

［9］赵鹏军，刘三阳.求解复杂函数优化问题的混合蛙跳算法［J］.计算机应用研究，2009，26(7):2435-2437.

［10］康冰，王曦辉，刘富.基于改进蚁群算法的搜索机器人路径规划［J］.吉林大学学报(工学版)，2014，44(4):1062-1068.

［11］Shakiba R，Najafipour M，Salehi M E.An improved PSObased path planning algorithm for humanoid soccer playing robots［C］// 2013 3rd Joint Conference of AI ＆ Robotics and 5th RoboCup Iran Open International Symposium(RIOS).2013:1-6.

［12］胡珂，李迅波，王振林.改进的人工蜂群算法性能［J］.计算机应用，2011，31(4):1107-1110.

［13］胡中华，赵敏.基于人工蜂群算法的TSP 仿真［J］.北京理工大学学报，2009，29(11):978-982.

［14］温长吉，王生生，于合龙，等.基于改进蜂群算法优化神经网络的玉米病害图像分割［J］.农业工程学报，2013，29(13):142-149.

［15］王慧颖，刘建军，王全洲.改进的人工蜂群算法在函数优化问题中的应用［J］.计算机工程与应用，2012，48(19):36-39.

［16］Ni Jianjun，Yang S X.Bioinspired neural network for realtime cooperative hunting by multirobots in unknown environments［J］.IEEE Transactions on Neural Networks，2011，22(12):2062-2077.

［17］Tian Yan-tao，Yang Mao，Qi Xin-yue，et al.Multi-robot task allocation for fire-disaster response based on reinforcement learning［C］// 2009 International Conference on Machine Learning and Cybernetics.2009，4:2312-2317.