基于粒子群算法的抄纸过程PID 神经元网络优化控制

吴新生

(广东科学技术职业学院广州学院，广东 广州 510640)

0 引言

抄纸过程是将稀释到一定浓度的纸浆在造纸机网部脱水，形成湿纸页，经压榨、烘干形成纸张。定量和水分是纸张质量重要的2 个参数，定量是每平方米纸的质量，用g/m2来表示;水分是每平方米纸的含水量，用%来表示。它们是抄纸过程中需要控制的参数。定量通过调节进浆阀的开度来增加或减少上网纸浆流量来进行控制;水分通过调节进入烘缸的蒸汽流量来增加或减少纸页的水分蒸发量来实现［1］。但是上网纸浆流量的变化不仅导致纸页定量的变化，也会引起纸页水分的变化;蒸汽流量的变化不仅导致纸页水分的变化，也会引起纸页定量的变化。因此，定量与水分的控制存在高度耦合［3］。加之，抄纸过程的流程长，除了容积延迟外，也存在很大的纯延迟，给定量水分控制带来很大的不利影响。文献［4-9］虽应用不同的解耦方法实现了定量与水分之间的解耦，也有文献通过应用Smith 预估控制克服了纯延迟的影响［6］，但是这些方法都需要建立精确的数学控制模型，而且不能同时解决抄纸过程控制的强耦合和长纯滞后这2 种问题。加之，抄纸过程复杂，获取精确的数学控制模型困难。因此，使用上述方法，很难取得最佳的控制效果。

本文尝试使用PID 神经元网络对抄纸过程定量水分进行解耦控制。PID 神经元网络不仅结构简单，而且具有非线性特点，且不需要建立精确的数学控制模型。仿真结果表明，设计的PID 神经元网络不仅实现了定量水分控制的完全解耦，而且克服了系统非线性和纯延迟对控制性能的影响，取得了令人满意的控制结果。

但是，PID 神经元网络的权值采用梯度学习法进行修正，初始权值随机给定，造成网络权值在修正过程中容易陷入局部最优。为了达到满意的学习效果，初始权值一般需要多次给定，但初始权值的给定方法很难保证每次给定均能达到期望的控制效果。为了改善上述情形，采用粒子群算法优选PID 神经网络的初始权值。研究发现，粒子群算法对PID 神经元网络初始权值进行优化选取，得到的PID 神经元网络在抄纸过程定量和水分的控制中取得了更佳控制效果。

1 抄纸过程定量水分的控制模型

文献［2］使用理论和经验相结合的方法，针对某一纸机对数学控制模型进行了简化降阶处理，最后得到简化的抄纸过程定量水分的数学控制模型为［2］:

其中，y1为纸页定量;y2为纸页水分;u1为进浆阀门开度;u2为烘缸蒸汽阀门开度。

从上式中也可以看出:进浆阀门开度的变化会同时引起纸页定量水分变化，烘缸蒸汽阀门开度变化会同时引起纸页定量水分变化，且纯延迟时间长。抄纸过程的控制系统是一个存在强耦合和纯延迟的系统。

2 基于PID 神经元网络的抄纸过程定量水分控制系统的设计

2.1 PID 神经元网络的原理与算法［10-11］

2.1.1 PID 神经元网络的原理图

双PID 神经元网络结构图如图1 所示。该网络从结构上可以分为输入层、隐含层、输出层。一个单PID 神经元网络进行一个控制量的控制，2 个控制量的PID 神经元网络包含2 个并列的相同子网络。抄纸过程的控制系统有定量和水分2 个控制量，采用双PID 神经元网络来进行控制。2 个子网络之间既相互独立，又在隐含层和输出层之间通过网络连接权相互联接。每个子网络的输入层有2 个神经元，分别接收控制量的目标值和当前值。每个子网络隐含层的神经元均由比例元、积分元和微分元构成，分别对应着PID 控制器的比例控制、积分控制和微分控制。从PID 神经元网络结构上可清楚地看出，PID 神经元网络控制不需要建立抄纸过程的精确数学控制模型。

图1 双PID 神经元网络结构图

2.1.2 双PID 神经元网络的学习算法

对于定量和水分2 个控制量的PID 神经元网络，在任意采样时刻k，各层神经元的计算如下:

1)输入层:该层包含4 个神经元，分别对应定量和水分的控制目标值和当前值的输入。神经元的输出数据等于输入数据，计算公式如下:

其中，usi为神经元的输出值，xsi为神经元的输入值，s=1，2 为并列子网络的序号，i=1，2。

2)隐含层:该层包含6 个神经元，包括2 个比例神经元、2 个积分神经元和2 个微分神经元。每个子网络的比例、积分和微分神经元的输入值均相同，计算公式如下:

6 个神经元输出的计算公式分别如下:

①比例神经元:

②积分神经元:

③微分神经元:

上面各式中，wsij为各子神经元网输入至隐含层的连接权值;s=1，2 为并联子网络的序号;j=1，2，3为每个子网络中隐含层神经元的序号。

3)输出层:该层有2 个神经元，对应定量和水分2 个输出量。输出层的输入为隐含层全部神经元的输出值加权和，计算公式如下:

神经元的输出为:

上式中，wsjh为隐含层至输出层的连接权值，h=1，2 为输出层的神经元序号。

学习过程主要是修正网络的连接权值。为了确定这些值，PID 神经元网络在控制过程中根据控制量误差按照梯度修正法修正权值，使得控制量不断接近控制目标值，权值修正的过程如下:

误差计算公式如下:

式中，n=2 为输出节点数，y 为预测输出，r 为目标值。

经过k 步训练，PID 神经元网络权值的修正采用增加动量项的改进误差反传算法，具体的公式如下:

①输入层到隐含层:

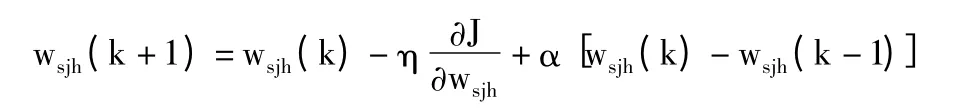
②隐含层到输出层:

其中，η 为学习速率，α 为惯性系数，0 ＜α ＜1。

2.2 基于PID 神经元网络的抄纸过程定量水分的闭环控制系统

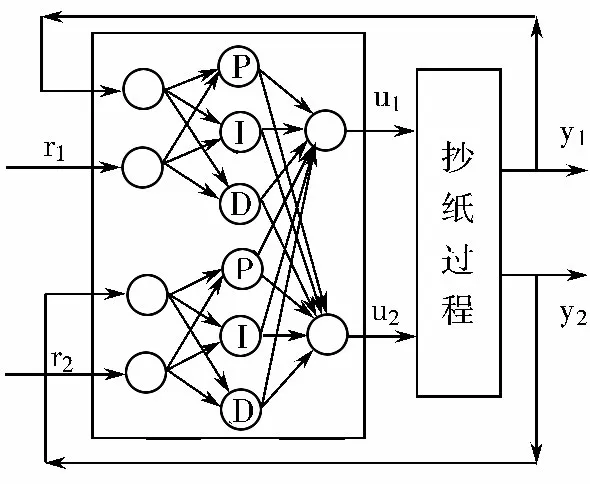
图2 PID 神经元网络闭环控制系统

抄纸过程的定量水分PID 神经元网络闭环控制系统原理如图2 所示。在系统中，r1和r2分别是系统的定量和水分给定值，y1和y2是系统的定量和水分输出，u1和u2分别是PID 神经元网络控制器的定量和水分控制律的输出。对于此系统，由于抄纸过程有定量和水分2 个控制量，所以选择包含了2 个单神经元网络组成的多神经元网络作为系统控制器。

2.3 PID 神经元网络初始权值的粒子群算法优化［12-17］

由于PID 神经网络采用梯度学习算法，随机选取网络的初始权值在学习过程中常易陷于局部最优。为了解决这个问题，尝试采用粒子群算法对PID 神经网络初始权值进行优选，方法如下:

在一个D 维的目标搜索空间中，首先初始化n个粒子，组成一个种群T={X1，X2，…，Xn}，其中，Xi=(xi1，xi2，…，xiD)，i=1，2，…，n，表示第i 个粒子在D 维空间的位置，vi=(vi1，vi2，…，viD)，i=1，2，…，n，表示第i 个粒子的速度。第i 个粒子搜索到的个体极值表示Pi=(Pi1，Pi2，…，PiD)，i=1，2，…，n，在整个粒子群中，所有粒子搜索到的全局极值表示为Pg=(Pg1，Pg2，…，PgD)，g∈{1，2，…，n}。则第i 个粒子按照下面的公式来更新自己的速度和位置:

上2 式中，ω 是惯性因子，i=1，2，…，n，k 是迭代代数，学习因子c1和c2为2 个正常数，分别调节向Pi和Pg方向飞行的步长，r1和r2是均匀分布于［0，1］之间的2 个随机数。为了控制和的各个分量在合理的区域内，需指定Vmax和Xmax，则Xi∈［-Xmax，Xmax］，Vi∈［-Vmax，Vmax］。为了达到较好寻优性能和效果，使用改进的粒子群优化算法来调整ω 惯性因子与学习因子c1和c2。

个体在算法搜索初期使用较大惯性权重，具有较强全局搜索能力，后期则使用较小惯性权重，提高局部搜索能力，这样可以减少迭代次数而找到最优解。故本文选择一种根据算法迭代次数使惯性权重线性递减的策略，惯性因子的计算公式如下:

式中，k 为当前的迭代代数，kmax为算法最大迭代代数。

个体在算法的初始阶段，具有大的“自身认知”部分和小的“群体认知”部分，以利于算法在整个寻优空间进行全局搜索，不至于过早陷入局部极小值;而在算法后期，应有小的“自身认知”部分和大的“群体认知”部分，以利于算法收敛于全局最优解，提高算法收敛速度和精度。故在进化过程中动态地调整学习因子c1和c2的值，计算公式如下:

上2 式中，kmax和k 分别为算法的最大迭代代数和当前代数。cmax和cmin为c1的最小值和最大值，其中0 ＜cmin＜cmax≤4。

3 仿真分析

抄纸过程定量和水分的PID 神经元网络是一个四输入二输出的网络，4 个输入分别是定量和水分的控制目标值和当前值，2 个输出分别是定量和水分的控制律输出，网络的初始权值分别为随机得到和使用粒子群算法优化得到，网络学习均取学习率η=0.01，惯性系数α=0.001，定量和水分的控制目标分别定为60 g/m2和6 %。网络初始权值随机得到的PID 神经元网络控制效果如图3 所示，控制总误差如图4 所示。PID 神经元网络的初始权值使用粒子群算法优化得到，PID 神经元网络控制效果如图5 所示，控制总误差如图6 所示。粒子群算法采用种群规模和进化代数分别为20 和50。

图3 PID 神经元网络控制效果(初始权值未优化)

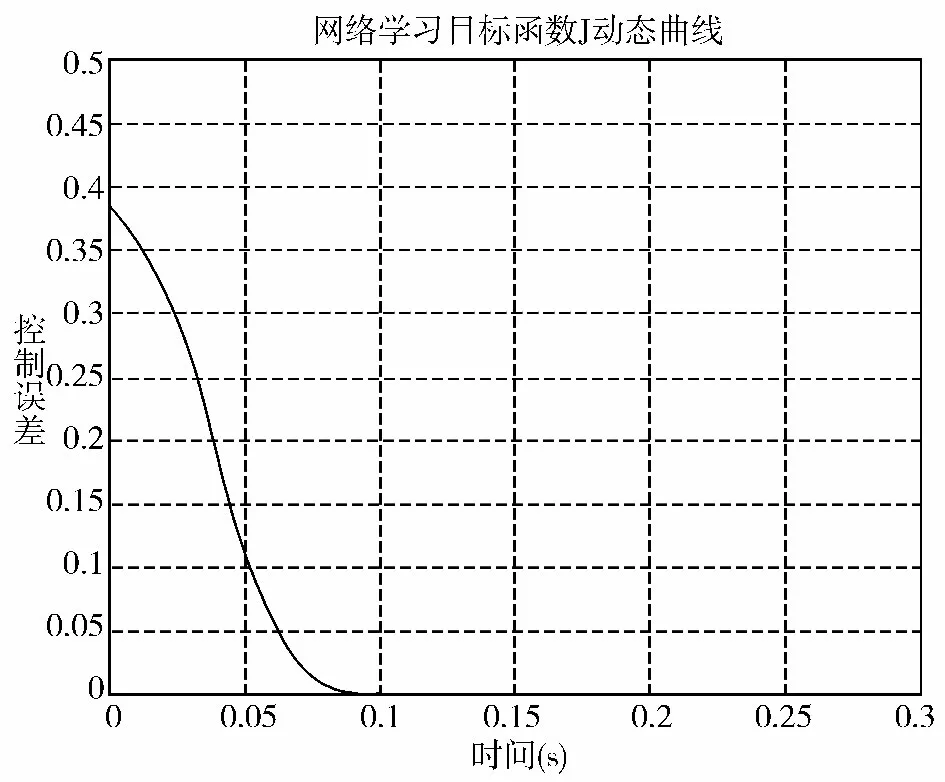
图4 PID 神经元网络控制误差曲线(初始权值未优化)

图5 PID 神经元网络控制效果(初始权值优化后)

图6 PID 神经元网络控制误差曲线(初始权值优化后)

通过仿真结果分析，可以发现:

1)从图3 和图5 可知，初始权值优化前后，采用抄纸过程定量和水分的PID 神经元控制系统，定量和水分的实际值都能平缓接近目标值，没有超调，PID神经元网络控制系统具有较好的动态控制特性。

2)比较图3 和图5，初始权值优化前后的PID 神经网络控制器都能够控制抄纸过程的定量水分系统，系统的实际输出达到控制目标，调节时间分别约为0.09 s 和0.02 s。这也说明优化后的PID 神经网络能够使系统保持更好的动态特性和更快的响应速度。

3)比较图4 和图6，初始权值优化前后的PID 神经元网络控制系统的控制误差平方均值分别在0.09 s、0.02 s后接近0。这也说明优化后的PID 神经元网络控制系统响应时间更短，控制系统的鲁棒性更强，控制效果更佳。

4 结束语

在抄纸过程定量水分的控制系统中，采用PID 神经元网络方法能充分发挥神经网络自学习的能力，可以在模型不精确的前提下，克服系统的强耦合、纯滞后和非线性，系统响应速度快、调节平稳性好，控制系统的控制质量较高。

粒子群算法优化后的抄纸过程定量水分PID 神经元网络控制系统的控制响应速度更快，具有更高的动态特性，控制系统的鲁棒性更强，能得到更高的控制精度。

［1］张玲，郑恩让.抄纸过程水分定量智能控制［J］.自动化仪表，2000，21(12):37-39.

［2］孙鑫，孙亚广，孙优贤.造纸过程定量水分的建模与控制［J］.中国造纸，2000(5):19-23.

［3］孙鑫，孙优贤.造纸过程定量水分解耦控制分析［J］.控制理论与应用，2001，18(S1):121-124.

［4］胡积胜，许宗保.解耦控制在纸机生产中的应用［J］.黑龙江造纸，2003，31(3):40-41.

［5］沈国江，胡丹，孙优贤.造纸过程定量水分神经网络建模和控制［J］.中国造纸学报，2004，19(1):151-155.

［6］张玲，郑恩让.多变量DMC 控制在水分定量中的应用［J］.自动化及仪器仪表，2004(3):34-36.

［7］熊淑贞，张根宝.抄纸过程定量水分控制仿真研究［J］.计算机仿真，2007，24(1):314-318.

［8］陈铁军，王梅.造纸过程定量和水分的结构分散化控制［J］.计算机工程与应用，2008，44(28):214-216.

［9］李艳，许合金.造纸过程定量水分的小波神经网络PID控制［J］.计算机仿真，2012，29(3):249-253.

［10］舒怀林.PID 神经元网络对强耦合带时延多变量系统的解耦控制［J］.控制理论与应用，1998，15(6):920-924.

［11］舒怀林，郭秀才，舒杰磊.注塑机料筒多段温度PID 神经网络解耦控制系统［J］.计算技术与自动化，2004，23(4):55-57.

［12］徐以山，曾碧，尹秀文，等.基于改进粒子群算法的BP神经网络及其应用［J］.计算机工程与应用，2009，45(35):233-235.

［13］沈学利，张红岩，张纪锁.改进粒子群算法对BP 神经网络的优化［J］.计算机系统应用，2010，19(2):57-61.

［14］张焱.新型粒子群算法［J］.计算机与现代化，2011(10):1-3.

［15］饶兴华，王文格，胡旭.多样性反馈与控制的粒子群优化算法［J］.计算机应用，2014，34(2):506-509，513.

［16］杨晨，孙欢.改进粒子群优化PID 的变风量空调控制策略［J］.计算机仿真，2014，31(6):424-428.

［17］衣治安，牟春苗，孙寅萍.基于改进粒子群算法的模糊神经网络［J］.计算机系统应用，2014，23(6):135-140.