The Representive of Metric Projection on the Finite Codimension Subspacein Banach Space

LIANG XIAO-BINAND HUANG SHI-XIANG

(1.School of Mathematics and Computer Science,Shangrao Normal College, Shangrao,Jiangxi,334000)

(2.School of Mathematics and Computer Science,Anhui Normal University, Wuhu,Anhui,241000)

Communicated by Ji You-qing

The Representive of Metric Projection on the Finite Codimension Subspace
in Banach Space

LIANG XIAO-BIN1,2AND HUANG SHI-XIANG1

(1.School of Mathematics and Computer Science,Shangrao Normal College, Shangrao,Jiangxi,334000)

(2.School of Mathematics and Computer Science,Anhui Normal University, Wuhu,Anhui,241000)

Communicated by Ji You-qing

In the paper we introduce the notions of the separation factor κ and give a representive of metric projection on an n-codimension subspace(or an affine set) under certain conditions in Banach space.Further,we obtain the distance formula from any point x to a finite n-codimension subspace.Results extend and improve the corresponding results in Hilbert space.

n-codimension,separation factor κ,weakly completely separated

1 Introduction

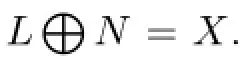
2 Preliminaries

Definition 2.1 Let X be a Banach space and L⊂X.Set

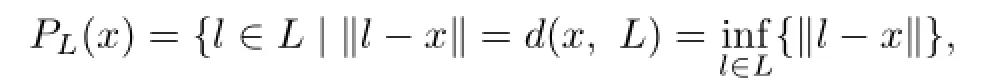
where d(x,L)denotes the distance from the point x to L.

Definition 2.2 Let X be a Banach space and X∗be the dual space of X.The set-valued map FX:X→X∗is defined by

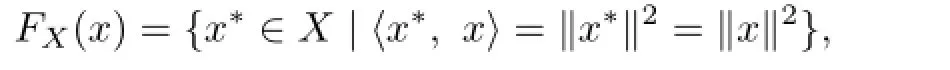
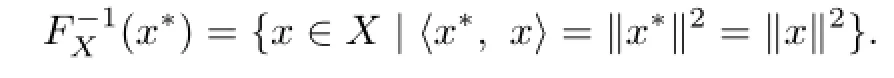
Definition 2.3 Let X be a reflexive Banach space and X∗∗be the quadratic dual space of X.The typical map J:X→X∗∗is defined by

and

Definition 2.4 Let X be a Banach space and N be an n-dimension subspace of X.The subspace L is called to be a finite n-codimension if L⊕N=X.

Lemma 2.1 Let X be a Banach space.Then L is a finite n-codimension subspace if and only if

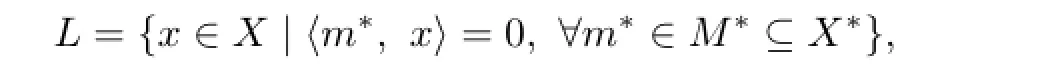
where M∗is an n-subspace of X∗.

Definition 2.5 Assume that E is an n-dimension subspace of the Banach X and e∗∈E∗. The extension by which e∗is extended toˆe∗∈X∗satisfying

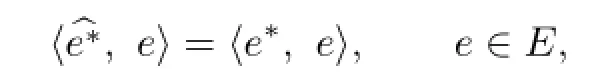
is called to be a value-preserving prolongation in E.If the value-preserving prolongation of e∗is norm-preserving,specially,we use e∗to denote it and say that it is a Hahn-Banach extension.

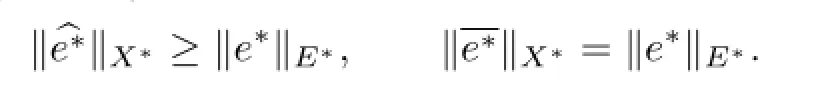
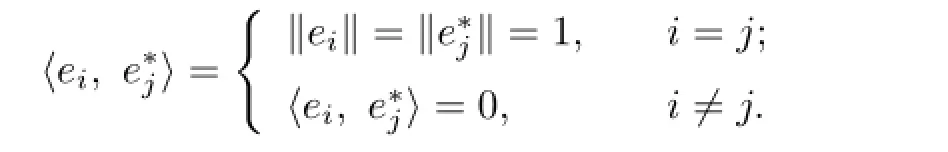
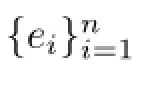
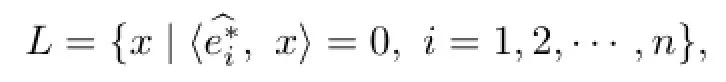
Definition 2.6 Let E be an n-subspace of Banach space X,andbe an

Auerbach system in E and E∗,respectively.By a value-preserving prolongation,can be extended toi=1,2,···,n.SetThen is also a valuepreserving prolongation of e∗.SetThen κ is called as a separation factor of E in X with span.Generally,κ≥1.If there is a certain value-preserving prolongation of the Auerbach system such that κ=1,then E is called to be weakly completely separated from X.

Remark 2.3 Let E be a 1-dimension subspace of the Banach space X.Then by Hahn-Banach theorem,E is weakly completely separated from X.In X∗,if M∗=span{m∗}is an 1-dimension subspace of X∗andthen M∗must be weakly completely separated.

Definition 2.7[10–11]Let X be a Banach space,N and L be closed spaces of X with L⊕N=X.If for any x=n+l∈X,n∈N,l∈L,∥x∥≥∥n∥,then N is Birkhoff orthogonal to L and N has a Birkhoff orthogonal decomposition in X,and L is a Birkhoff orthogonal complement of N.

Lemma 2.2 Let N be an n-subspace of Banach space X.Then N has a Birkhoff orthogonal decomposition if and only if N can be weakly completely separated.

Proof.⇒.If N is Birkhoff orthogonal to L,we can chooseandto be the Auerbach systems of N and N∗,respectively.And at the same time,we can extend AN(ei)to the following value-preserving prolongation:

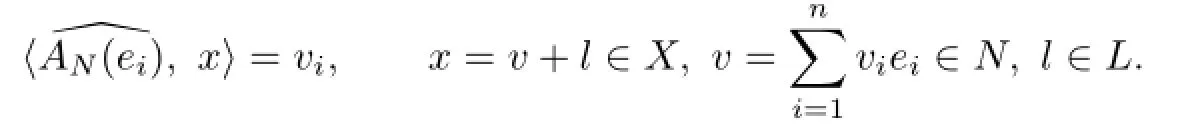
Set

Since∥x∥≥∥v∥,we can obtain

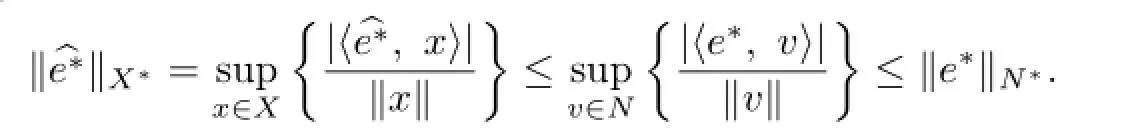
⇐.Conversely,N and X can be weakly completely separated.Therefore,there existin N and N∗,respectively,which form an Auerbach system.At the same time,there exists a value-preserving prolongation such thatand

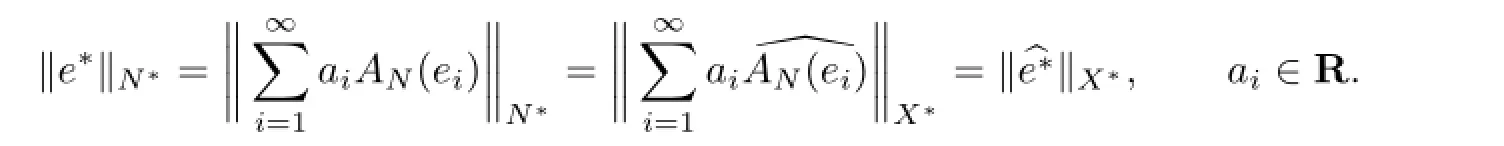
Set

Therefore,N is Birkhoff orthogonal to L.

3 Main Results and Applications

Theorem 3.1 (i)Let X be a reflexive and strictly convex Banach space and M∗⊂X∗be an n-dimensional subspace which is weakly completely separated from X∗(or in X∗,there is a Birkhoff orthogonal decomposition about M∗).If L={x|〈m∗,x〉=0,m∗∈M∗⊆X∗}, then,for any x∈X,we have

(ii)Only if X is reflexive,then,for any x∈X,we have

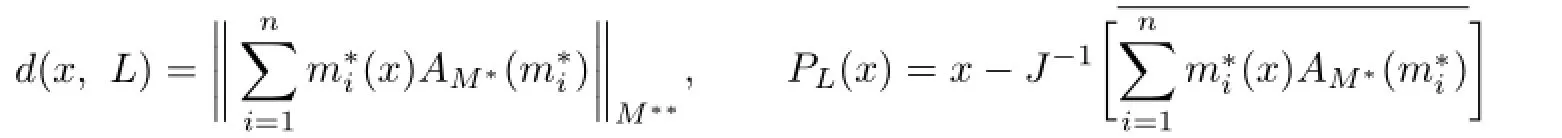
Proof. (i)By Lemma 2.2,that M∗has a Birkhoff orthogonal decomposition is equivalent to that it can be weakly completely separated.Now we only assume that M∗is weakly completely separated,and hence,there exist span,spanandwhich form an Auerbach system of M∗and M∗∗,respectively,

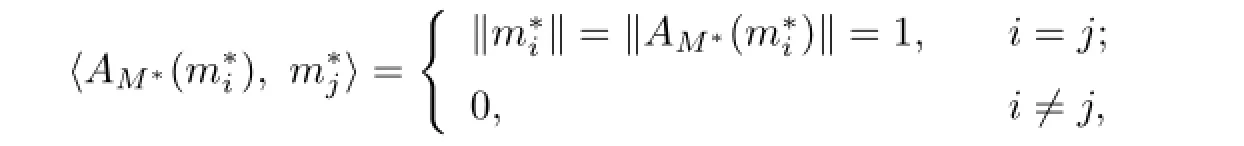
Since X is reflexive,we can seti=1,2,···,n.Obviously,we can obtain

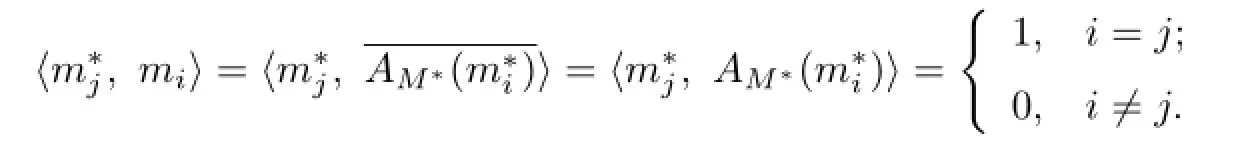
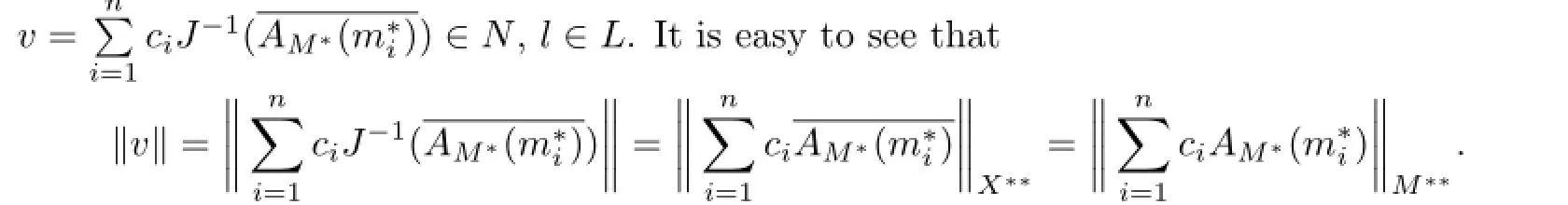
As M∗is an n-subspace,there exists an m∗∈M∗with∥m∗∥=1 such that

Since

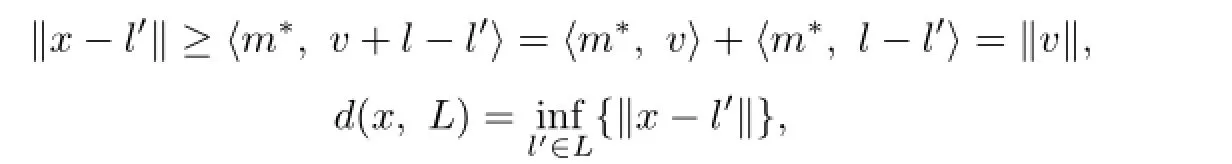
we know l∈PL(x).Since

we have

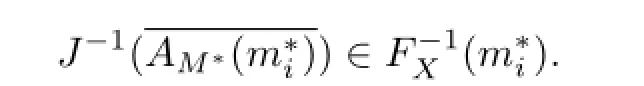
Since X is strictly convex,we know that X∗is smooth andis a singleton.Namely, we have

Hence,

that is,

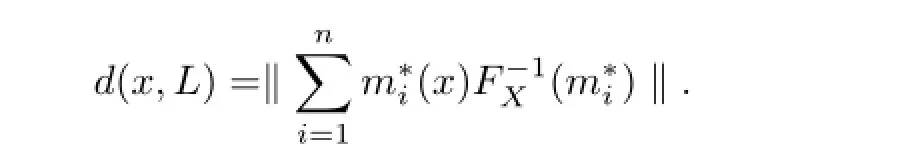
Therefore X is strictly convex.So PL(x)is unique and therefore(i)is proved.

(ii)By the proof of(i),we have

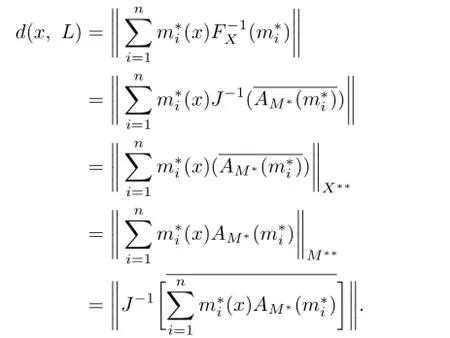
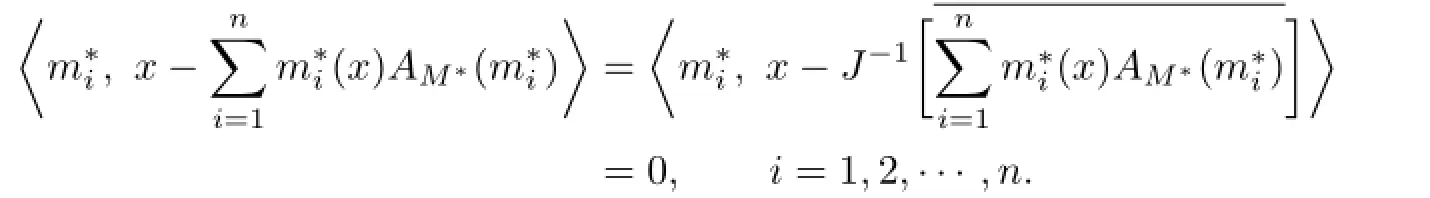
Hence

and then

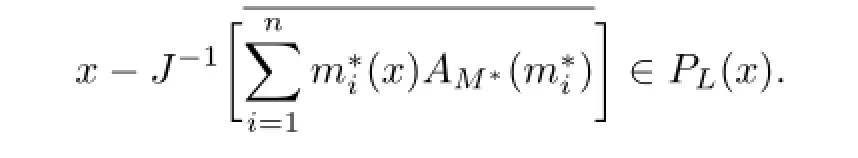
Conversely,if l′∈PL(x),we have

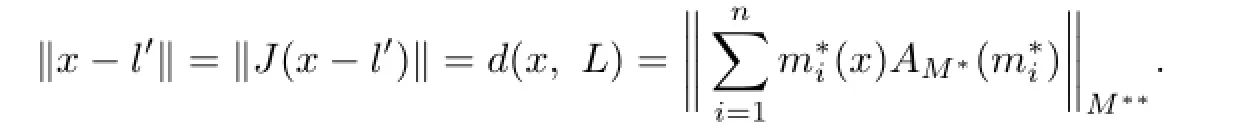
Noting that

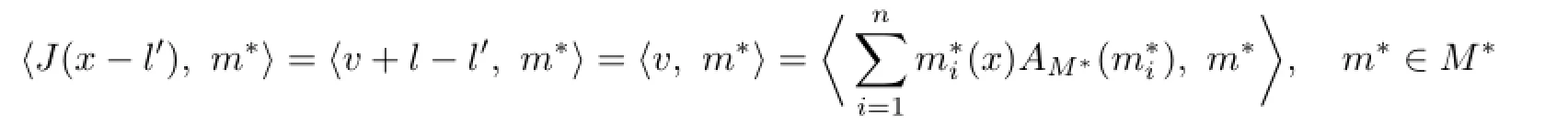
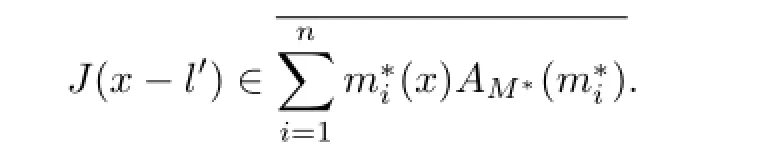
So

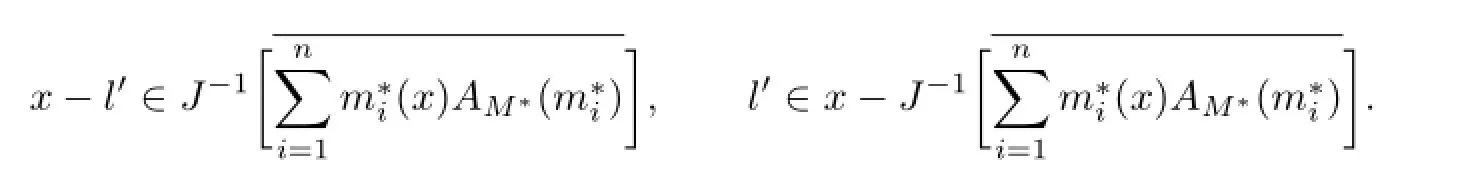
Hence

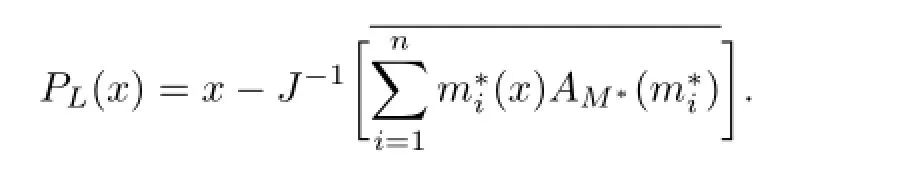
Conclusion 3.1 Let X be a reflexive and strictly convex Banach space,and spanM∗⊂X∗be an n-dimensional subspace which is weakly completely separated from X∗onThen we have

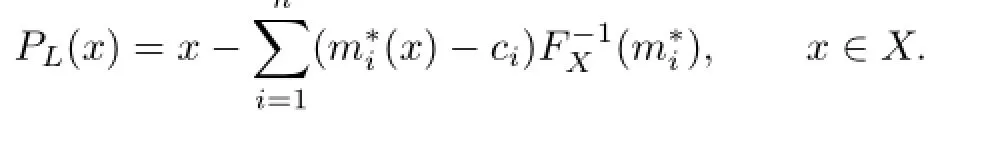
Proof.By

the proof is completed.

Conclusion 3.2 Let X be a real Hilbert space,

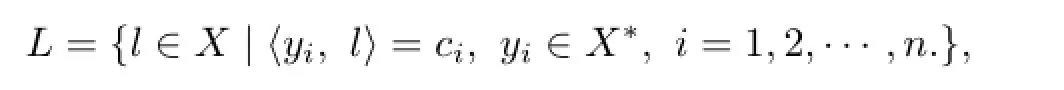
and{y1,y2,···,yn}be linearly independent.Then we have

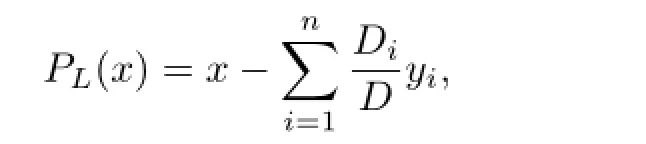
where D=Gram(y1,y2,···,yn),Di=GramProof.Let{y1,y2,···,yn}be Schmidt's orthogonalization constructsObviously,this makes the conditions of Conclusion 3.1 hold.By Conclusion 3.1 and〈yi,x−l〉=〈yi,x〉−ci,Conclusion 3.2 holds.

Conclusion 3.3[7–9]Let X be a reflexive Banach space(or X be a Banach space andThen we have

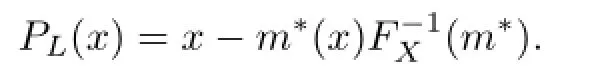
Now we show some applications of Theorem 3.1 and Conclusions as follows.

Example 3.1

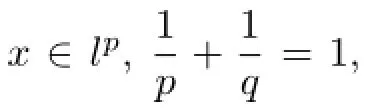
Example 3.2 We describe the minimum norm problem with some constrained conditions as follows:

For example,there is such an classic optimal control problem:

Let u(t)be the field current at time t.Angular velocity is denoted as ω(t),the contact equation is

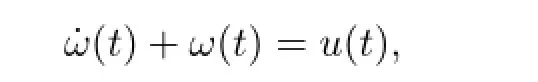
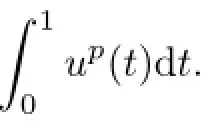
It is easy to see that the problem can be converted into:

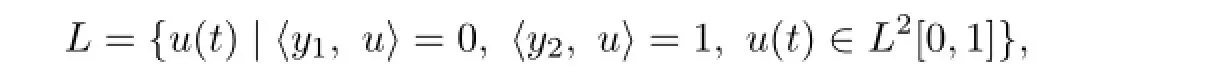
calculating PL(0),whereUsing Conclusion 3.3,by straightly calculating,we have

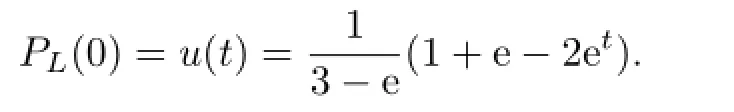
In fact,if the formula of Theorem 3.1(i)holds for all finite codimension subspace L of X,then PLmust be linear.On the contrary,it does not except unless X is isometric isomorphism to a Hilbert space,or there exists one subspace L of X whose dimension is larger than 1 such that PLis nonlinear.Of course,when we choose an Auerbach system for a certain extension,if κ＞1,and the error is small enough,then it makes sense to use the formula.Here we only give some simple discussion on the Banach spaces with countable Bases.

i=1,2,···,n.

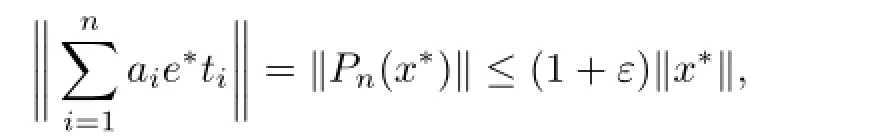
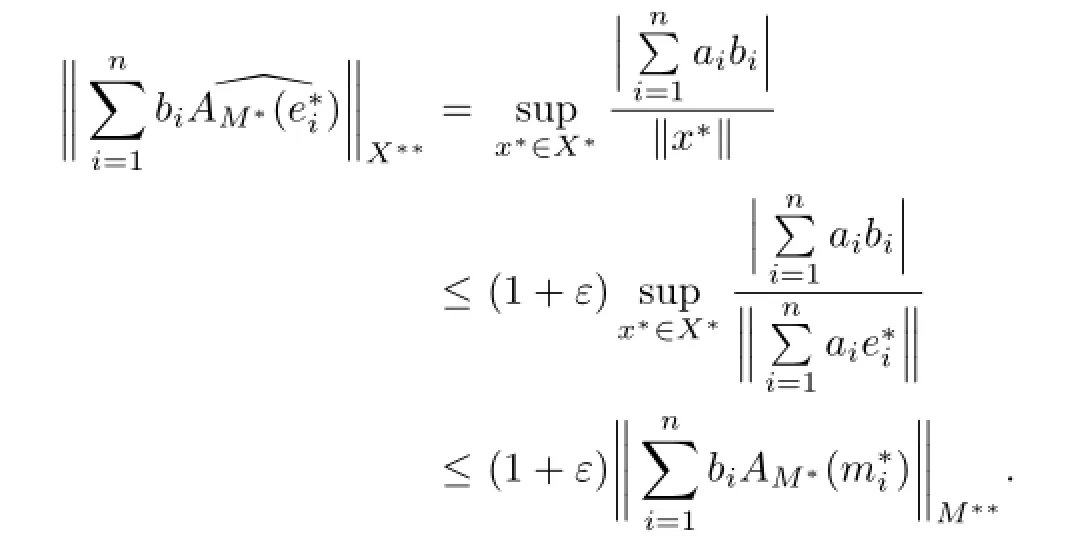
Hence,by the value-preserving prolongation,we have

It is easy to show that

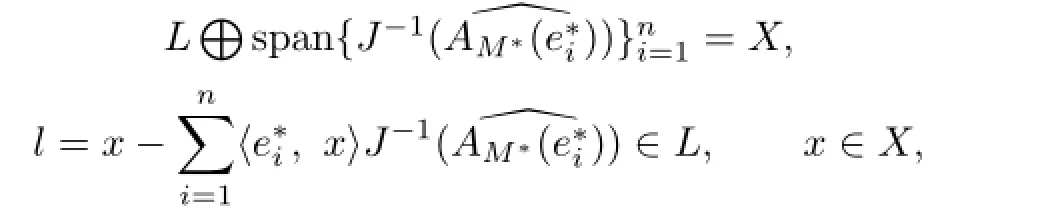
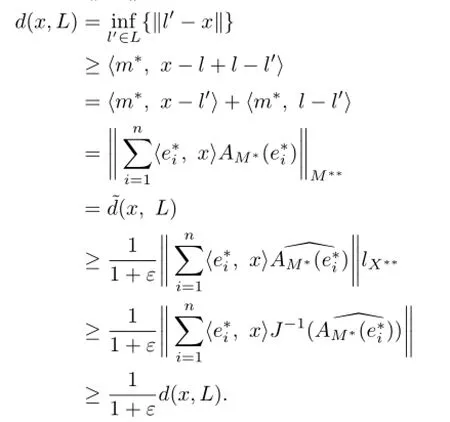
Therefore,

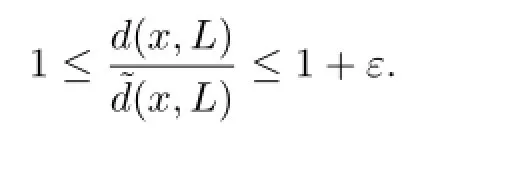
[1]Vakhrameev S A.Hilbert manifolds with corners of finite codimension and the theory of optimal control.J.Soviet Mathematics,1991,53(2):176–223.

[2]Oshman E V.The continuity of the metric projection on a subspace of finite codimension in the space of continuous functions.Math.Notes,1976,19(4):324–328.

[3]Fang X N,Wang J H.Convexity and the continuity of metric projections.Math.Appl.,2001, 14(1):47–51.

[4]Fedorov V M.Characterization of Chebyshev cones of finite dimension or finite codimension. Moscow Univ.Math.Bull.,2008,63(6):229–244.

[5]Liang X B,Huang S X.On the Representation of linear isometries between the E(2)type real spaces.Acta Math.Scientia,Ser.A,2010,30(4):1088–1093.

[6]Ni R X,Ke Y Q.Generalized orthogonal decomposition theorem and the Tseng-metric generalized inverse.Chinese Ann.Math.Ser.A,2005,26(2):269–274.

[7]Wang Y W,Yu J F.The character and representive of a class of metric projection in Banach space.Acta Math.Sci.,Ser.A,2001,21(1):29–35.

[8]Wang J H.The metric projections in nonreflexive Banach space.Acta Math.Sci.,Ser.A,2006, 26(6):840–846.

[9]Ni R X.The representive of metric projection on the linear Manifold in arbitary Banach space. J.Math.Res.Exposition,2005,25(1):99–103.

[10]Birkhoff G.Orthogonality in linear metric space.Duke Math.,1935,1:169–172.

[11]Li C K,Schneider H.Orthogonality of matrices.Linear Algebra Appl.,2002,347:115–122.

A

1674-5647(2015)04-0373-10

10.13447/j.1674-5647.2015.04.09

Received date:March 24,2015.

The NSF(11161039,11461056)of China.

E-mail address:liangxiaobin2004@126.com(Liang X B).

2010 MR subject classification:41A65,46B20