On Weakly P.P.Rings

XIANG YUE-MING,OUyANG LUN-QUNAND WANG SHU-GUI

(1.Department of Mathematics and Applied Mathematics,Huaihua University,Huaihua, Hunan,418000)

(2.Department of Mathematics,Hunan University of Science and Technology,Xiangtan, Hunan,411201)

Communicated by Du Xian-kun

On Weakly P.P.Rings

XIANG YUE-MING1,OUyANG LUN-QUN2AND WANG SHU-GUI1

(1.Department of Mathematics and Applied Mathematics,Huaihua University,Huaihua, Hunan,418000)

(2.Department of Mathematics,Hunan University of Science and Technology,Xiangtan, Hunan,411201)

Communicated by Du Xian-kun

We introduce,in this paper,the right weakly p.p.rings as the generalization of right p.p.rings.It is shown that many properties of the right p.p.rings can be extended onto the right weakly p.p.rings.Relative examples are constructed.As applications,we also characterize the regular rings and the semisimple rings in terms of the right weakly p.p.rings.

weakly p.p.ring,GP-injective module,regular ring

1 Introduction

Throughout this paper,R is an associative ring with identity and all modules are unitary. J(R)and Z(RR)denote,respectively,the Jacobson radical and the right singular ideal of R. If X is a subset of R,the right(resp.left)annihilator of X in R is denoted by r(X)(resp. l(X)).If X={a},we usually abbreviate it to r(a)(resp.l(a)).For the usual notations,we refer the readers to[1–3].

A ring R is called Baer(see[2])if the right annihilator of every nonempty subset of R is generated by an idempotent.The class of Baer rings play a special role in the theory of rings of operators in functional analysis.The notion of p.p.rings is closely related to that of Baer rings.Recall that a ring R is said to be right p.p.(see[4])(or right Rickart)provided that every principal right ideal is projective,or equivalently the right annihilator of any element of R is a summand of RR.A ring is called a p.p.ring if it is both left and right p.p.ring. We say that an element a of R is right p.p.if aR is projective,or equivalently,if r(a)=eRfor some e2=e∈R.Obviously,R is a right p.p.ring if and only if every element of R is right p.p.The p.p.rings and their generalizations have been extensively studied by many authors(see[4–12]).A ring R is called a generalized right p.p.ring if for any a∈R,the right ideal anR is projective for some positive integer n,depending on a,or equivalently,if for any a∈R,the right annihilator of anis generated by an idempotent for some positive integer n,depending on a.

A right R-module M is called GP-injective(see[13])(or Y J-injective in[14])if,for any 0̸=a∈R,there exists a positive integer n such that an̸=0 and any right R-homomorphism from anR to M extends to one from R to M.A right R-module N is said to be P-injective provided that for any a∈R,any right R-homomorphism from aR to N can extend to one from R to N.A ring R is right GP-injective(resp.P-injective)if R is GP-injective(resp. P-injective)as a right R-module.It was shown that left GP-injective rings are the proper generalization of left P-injective rings(see[15]).In the recent paper,Mao et al.[8]proved that R is a right p.p.ring if and only if every quotient module of any(P-)injective right R-module is P-injective.It was also shown that a ring R is regular if and only if R is a right p.p.and right P-injective ring if and only if R is a right p.p.and right C2 ring.

This inspires us to develop right weakly p.p.rings.We say that,in this paper,a nonzero element a of R is called right weakly p.p.if there exists a positive integer n such that an̸=0 and anR is projective,or equivalently,r(an)=eR for some e2=e∈R.The ring R is said to be the right weakly p.p.provided that every nonzero element of R is right weakly p.p. Some examples are given to show that the right weakly p.p.elements need not be the right p.p.elements and the generalized right p.p.rings need not be the right weakly p.p.rings. Many properties of the right p.p.rings are extended onto the right weakly p.p.rings.In Section 3 of the present paper,we investigate the extensions of the right weakly p.p.rings. It is proven that a ring R is right semihereditary if and only if the matrix ring Mn(R)is right weakly p.p.for every n≥1.Section 4 is devoted to the applications of the right weakly p.p.rings.We characterize(von Neumann)regular rings and the semisimple Artinian rings in terms of the right weakly p.p.rings.Several well-known results are also extended.

2 Right Weakly P.P.Rings

We start this section with the definition.

Definition 2.1 A nonzero element a of R is called right weakly p.p.if there exists a positive integer n such that an̸=0 and anR is projective,or equivalently,r(an)=eR for some e2=e∈R.The ring R is said to be right weakly p.p.provided that any nonzero element of R is right weakly p.p.Similarly,we have the concepts of left weakly p.p.elements and rings.

Remark 2.1 (1)Obviously,the right p.p.rings are right weakly p.p.and the right weakly p.p.rings are the right generalized p.p.rings.

(2)Recall that R is called right PS(see[10])if each minimal right ideal is projective. We claim that the right weakly p.p.rings are right PS.Indeed,in view of[3,Lemma 10.22], every minimal right ideal of R is either nilpotent or a direct summand of R.

Unfortunately,we cannot find a ring R that is right weakly p.p.but not right p.p. However,the below example shows that the right weakly p.p.elements need not be right p.p.

Example 2.1 Let F be a field with an isomorphism x→¯x from F to a subfield¯F.Let R denote the left F-space on basis{1,c},where c2=0 and cx=¯xc for all x∈F.Write S=R⊕R.Choose y∈F−¯F and put a=yc.Then α=(1,a)∈S and α2=(1,0), whence α is a right weakly p.p.element in S.Note that r(a)⊆J(R),then a is not a right p.p.element in R.Thus α=(1,a)is not a right p.p.element in S.

The next example is constructed to show that right PS rings need not be right weakly p.p.

We now present an example,due to Chase,of a ring that is left weakly p.p.but not right weakly p.p.

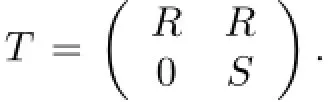
A ring is called reduced if it has no nonzero nilpotent elements.A ring R is called semicommutative if for every a∈R,l(a)is an ideal of R.A ring is called abelian if every idempotent in it is central.It is easy to see that the reduced rings are the semicommutative and semicommutative rings are abelian.But both converses are false.

Lemma 2.1 If R is a right weakly p.p.ring,then the following statements are equivalent:

(1)R is a reduced ring;

(2)R is a semicommutative ring;

(3)R is an abelian ring.Proof. It suffices to prove that(3)implies(1).Let 0̸=a∈R with a2=0.Then r(a)=eR for some e2=e∈R since R is right weakly p.p.Note that a∈r(a),hence a=ea=ae=0,a contradiction.Therefore,R is a reduced ring.

Lemma 2.2 Let R be an abelian,right weakly p.p.ring.Then R is a p.p.ring.

Proof. For any 0̸=a∈R,there exists a positive integer n such that an̸=0 and r(an)=eR for some e2=e∈R.Then(ae)n=ane=0 since R is abelian.Thus ae=0 since R is reduced by Lemma 2.1,whence r(a)=eR.By Lemma 2.1,we also have r(a)=l(a).Therefore,R is a p.p.ring.This completes the proof.

By Lemma 2.2,commutative weakly p.p.rings are p.p.rings.

The below examples follow from Examples 2 and 3 in[5],which show that a generalized p.p.ring need not to be weakly p.p.

Example 2.4 Let Z2be the field of integers modulo 2,and

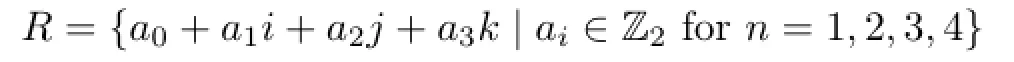
be the Hamilton quaternions over Z2.It was proven that R is a commutative generalized p.p.ring but not a p.p.ring.Then R is not a weakly p.p.ring by Lemma 2.2.

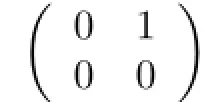
It was shown that the right p.p.rings are right nonsingular(see[3])and have no nonzero central nilpotent elements(see[5]).Now we extend those properties onto the right weakly p.p.rings.

Proposition 2.1 Right weakly p.p.rings are right nonsingular.

Proof. Suppose that Z(RR)̸=0.Then Z(RR)contains nonzero nilpotent elements.In fact,assume that Z(RR)is reduced and let 0̸=x∈Z(RR),so r(x)is an essential right ideal of R.Thus r(x)∩xR̸=0,and hence there exists an r∈R such that xr̸=0 and x2r=0.So we have(xrx)2=0,whence xrx=0.It implies(xr)2=0,and hence xr=0, a contradiction.

Now take 0̸=b∈Z(RR)with b2=0.Then r(b)=eR for some e2=e∈R since R is right weakly p.p.Thus r(b)cannot be essential in RR,which contradicts with b∈Z(RR). Therefore,R is right nonsingular.This completes the proof.

The ring T in Example 2.3 is right nonsingular but not right weakly p.p.

Proposition 2.2 Right weakly p.p.rings have no nonzero central nilpotent elements.

Proof. Assume that there exists 0̸=a∈C(R)such that am=0 and am−1̸=0 for some positive integer m.Since R is right weakly p.p.,there exists a positive integer n≤m−1 such that an̸=0 and r(an)=eR for some e2=e∈R.But am−n∈r(an)and an̸=0,so neither e=0 nor e=1.We have

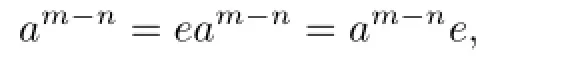
since am−n∈C(R).Thus

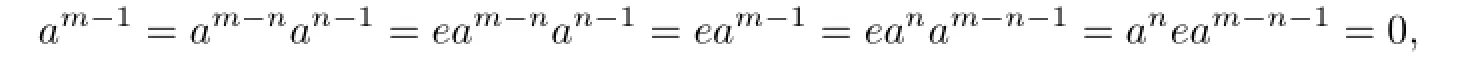
a contradiction.We then get the result.

Remark 2.2 By Lemma 2.1 or Proposition 2.2,commutative weakly p.p.rings are reduced.But commutative reduced rings may be not weakly p.p.For example,let S0=Z2, the ring of integers modulo 2,S1=Z2∗Z2,S2=S1∗Z2,···,Sn=Sn−1∗Z2,···,where the operations on Snare as follows:for(a,¯b),(c,¯d)∈Snwith a,c∈Sn−1,(a,¯b)+(c,¯d)= (a+c,¯b+¯d)and(a,¯b)(c,¯d)=(ac+bc+da,¯bd),where n=1,2,···Next define

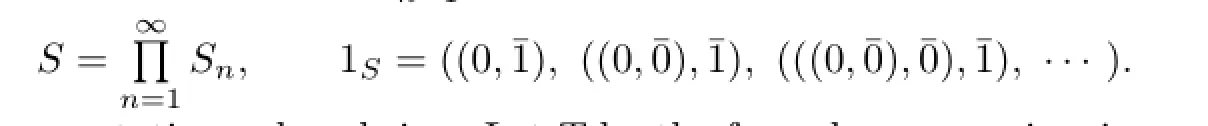
Then R is a commutative reduced ring.Let T be the formal power series ring over R.Then T is commutative reduced,but not p.p.by the argument in[6,Example 4].So T is not weakly p.p.by Lemma 2.2.

Lemma 2.3 Let R be a right weakly p.p.ring.Then any nonzero left annihilator L contains a nonzero idempotent.

Proof. Let S=r(L)so that L=l(S).Fix a nonzero element a∈L.Since R is right weakly p.p.,there exists a positive integer n such that an̸=0 and r(an)=eR for some e2=e∈R.But

which implies that

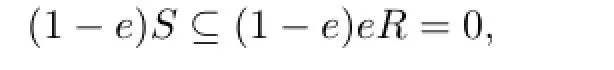
so L=l(S)contains the nonzero idempotent 1−e.

Theorem 2.1 Let R be a ring that has no infinite set of nonzero orthogonal idempotents. Then the following statements are equivalent:

(1)R is a Baer ring;

(2)R is a right weakly p.p.ring;

(3)R is a left weakly p.p.ring.

If any of these conditions holds,then R satisfies ACC and DCC on left(resp.right) annihilators.Proof. It is enough to prove that(2)implies(1).We first consider any nonzero left annihilator L.By[3,Proposition 6.59],the direct summands of R satisfy the DCC.Among all nonzero idempotents in L(which exist by Lemma 2.3),choose e with R(1−e)=l(e) minimal.Now we prove that L∩l(e)=0.Otherwise,0̸=L∩l(e)=l(S∪e),where S is a subset of R.By Lemma 2.3,there exists a nonzero idempotent f in l(S∪e).Write e′=e+(1−e)f.Then we have e′2=e′and e′e=e.It implies that e′̸=0.Note that fe=0 and fe′=f(1−e)f=f̸=0,hence l(e′)⊂l(e).This contradicts the choice of e. Thus,for any x∈L,x−xe∈L∩l(e)=0,and hence x=xe.This shows that L=Re,as desired.This completes the proof.

We obtain the necessary and sufficient conditions under which R is a right weakly p.p. ring as follows.

Theorem 2.2 For a ring R,the following statements are equivalent:

(1)R is a right weakly p.p.ring;

(2)Every quotient of any P-injective right R-module is GP-injective;

(3)Every quotient of any injective right R-module is GP-injective;

(4)The sum of two injective submodules of any right R-module is GP-injective.

Proof. (1)⇒(2).Let M be any P-injective right R-module and N be any submodule of M.It is enough to show that M/N is GP-injective.For any 0̸=a∈R,there exists a positive integer n such that an̸=0 and anR is projective by hypothesis.Let i:anR→R be the inclusion and π:M→M/N be the canonical map.For any f:anR→M/N,there exists g:anR→M such that πg=f since anR is projective.Thus there is h:R→M such that hi=g since M is P-injective,whence(πh)i=f.Then(2)follows.

(2)⇒(3)is clear.

(3)⇒(1).Let E be an injective right R-module and E′be any quotient of E.Then E′is GP-injective by(3).For any 0̸=a∈R,there exists a positive integer n such that an̸=0 and any homomorphism h:anR→E′can extend to g:R→E′,i.e.,h=gi,where i:anR→R is inclusion.Then there is l:R→E such that πl=g since R is projective, where π:E→ E′is the canonical map.It follows that π(li)=gi=h.Thus anR is projective by[1,Proposition 5.1]and the result holds.

(3)⇒(4).Let I1,I2be injective submodules of a right R-module M.Then I1⊕I2is still injective and I1+I2is a quotient.By(3),I1+I2is GP-injective.

(4)⇒(3).Consider an injective right R-module M and N⊆M.Let π:M →M/N be the natural epimorphism.The homomorphism g:M →M⊕(M/N)given by g(m)= (m,π(m)),m∈M is well-defined.Note that M⊕(M/N)is the sum of the two submodules M⊕(0)and π(M),which are both injective.By(4),M⊕(M/N)is GP-injective,so M/N is also GP-injective.This completes the proof.

If R is an abelian ring,then R is a p.p.ring if and only if every divisible right R-module is P-injective[4,Theorem 8].Here we have:

Proposition 2.3 If R is an abelian ring,then the following statements are equivalent:

(1)R is a p.p.ring;

(2)R is a right weakly p.p.ring.;

(3)Every divisible right R-module is GP-injective.

Proof. (1)⇔(2)follows from Lemma 2.2.

(1)⇒(3)is the result of[4,Theorem 8]since the right P-injective R-modules are right GP-injective.

(3)⇒(2).Let M be an injective right R-module.Then it is divisible.Thus every quotient module N of M is divisible,hence N is GP-injective by hypothesis.Therefore,by Theorem 2.1,R is right weakly p.p.

3 Extensions

In the present section,we first prove that if R is right weakly p.p.,then the same is true for the corner ring eRe,in which e2=e∈R.A slight modification of the proof of[5, Proposition 9(i)]yields the next proposition.

Proposition 3.1 Let R be a ring and e2=e∈R.If R is a right weakly p.p.ring,then so is eRe.

Proof. Let 0̸=a∈eRe.Then there exists a positive integer n such that an̸=0 and rR(an)=fR for some f2=f∈R since R is right weakly p.p.Note that

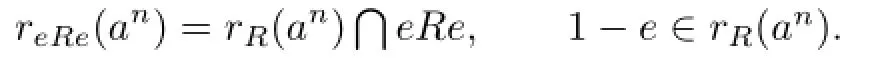
So 1−e=f(1−e)and ef=efe.Write ef=g.Then g2=g∈eRe.So

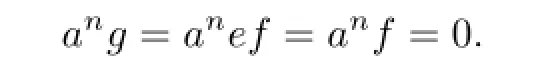
Thus,for any b∈reRe(an),b=eb=efb=gb∈geRe.It implies reRe(an)=geRe.

Therefore,eRe is a right weakly p.p.ring.This completes the proof.

A ring R is called right semihereditary if every finitely generated right ideal in R is projective.It was proved that a ring R is right semihereditary if and only if the matrix ring Mn(R)is right p.p.for every n≥1(see[3,Proposition 7.63]).We show that a ring R is right semihereditary if and only if the matrix ring Mn(R)is right weakly p.p.for every n≥1.Let{Eij:i,j=1,···,n}be the matrix units.

Lemma 3.1 Let S=Mn(R)and 0̸=a∈R.If(aE1n)S is projective in S,then aR is projective in R.

Proof. If(aE1n)S is a projective right S-module,then(aE1n)S is also projective as a right R-module.Write aR=I.Note that

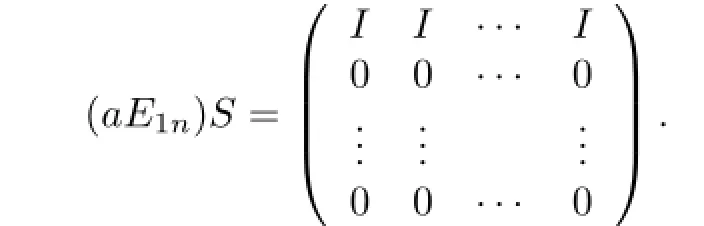
Lemma 3.2 If Mn(R)is right weakly p.p.for some n≥2,then R is right p.p.

Proof. For 0̸=a∈R,let α=aE1n.Since S=Mn(R)is right weakly p.p.,there exists an n＞0 such that αn̸=0 and αnS is projective as a right S-module.Since α2=0,so αS must be projective.By Lemma 3.1,aR is projective as a right R-module.So R is a right p.p.ring.This completes the proof.

We are now in a position to prove the next theorem.

Theorem 3.1 A ring R is right semihereditary if and only if the matrix ring Mn(R)is right weakly p.p.for every n≥1.

Proof. It is enough to prove the sufficiency.Suppose that every matrix ring Mm(R) is a right weakly p.p.ring.For n＞0,M2(Mn(R))～=M2n(R)is right weakly p.p.by hypothesis.So Mn(R)is right p.p.by Lemma 3.2.Thus,by[3,Proposition 7.63],R is right semihereditary.This completes the proof.

Let R be a ring and M be a bimodule over R.The trivial extension of R and M is R∝M={(a,x)|a∈R,x∈M}with addition defined by componentwise and multiplication defined by(a,x)(b,y)=(ab,ay+xb).

Proposition 3.2 Let S=R∝R.If S is a right weakly p.p.ring,then R is a right p.p. ring.

Proof. For any a∈R,α=(0,a)∈S and α2=0.Since S is right weakly p.p.,rS(α)=e1S for someNote that rS(α)=rR(a)∝R and e1=(e,x)for some e2=e∈R, x∈R,then rR(a)=eR for some e2=e∈R.Therefore,R is a right p.p.ring.This completes the proof.

The following results are similar to that of[12].

Proposition 3.3 Let R be a subring of a ring S both with the same identity.Suppose that S is a free left R-module with a basis G such that 1∈G and ag=ga for all a∈R and all g∈G.If S is right weakly p.p.,then so is R.

Proof. For 0̸=a∈R.Since S is right weakly p.p.,there exists a positive integer n such that an̸=0 and rS(an)=eS,where e2=e∈S.Write e=e0g0+···+engn,where g0=1 and gi∈G are distinct and ei∈R.Then

which shows that anei=0 for i=0,···,n.Thus ei∈rS(an)=eS,which implies that ei=eei.It follows thatBecausewe haveOn the other hand,if

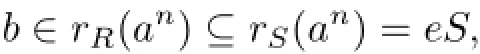
then

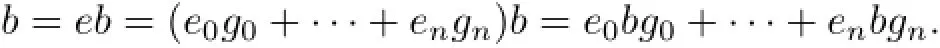
So b=e0b∈e0R.Therefore,rR(an)=e0R.

Corollary 3.2 If R[x]or R[x,x−1]is right weakly p.p.,then so is R.

Proof. R[x]and R[x,x−l]are free R-modules with bases

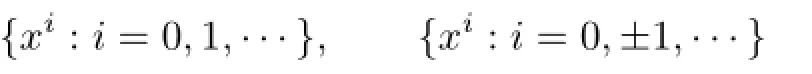
satisfying the assumptions of Proposition 3.3.

4 Applications

Recall that an element a∈R is(von Neumann)regular if a=aba for some b∈R.An element a is generalized π-regular if there exists a positive integer n such that an=anba for some b∈R.R is called regular(resp.generalized π-regular)if every element in R is regular(resp.generalized π-regular).It was proven that a ring R is regular if and only if R is left p.p.and left GP-injective if and only if R is right p.p.and right GP-injective(see [16,Theorem 2.9]).In this section,we give some new characterizations of the regular rings and the semisimple Artinian rings in terms of the right weakly p.p.rings.

The next lemma(see[16,Theorem 2.2])is used in the sequel.

Lemma 4.1 For a ring R,the following statements are equivalent:

(1)R is regular;

(2)N1(R)={0̸=a∈R|a2=0}is regular and R is generalized π-regular.

Theorem 4.1 Let R be a ring.Then the following statements are equivalent:

(1)R is a regular ring;

(2)R is a right weakly p.p.and right GP-injective ring;

(3)R is a right weakly p.p.and right C2 ring;

(4)R is a right weakly p.p.ring and every maximal right ideal in it is P-injective.

Proof. (1)⇒(2),(1)⇒(3)and(1)⇒(4)are trivial.

(2)⇒(1).By Lemma 4.1,it suffices to prove that N1(R)={0̸=b∈R|b2=0}is regular and R is generalized π-regular.Let b∈N1(R).Then lr(b)=Rb since R is right GP-injective.By hypothesis,r(b)=eR,where e2=e∈R,whence Rb=lr(b)=l(eR)= R(1−e).Thus b is regular.So N1(R)is regular.

Now let 0̸=a∈R.Then there exists a positive integer m such that am̸=0 and lr(am)=Ramsince R is right GP-injective.Set c=am̸=0 and I=lr(am)=Ram.Then there exists a positive integer t such that ct̸=0 and r(ct)=fR for some f2=f∈R.Thusct=ct(1−f).Note that R(1−f)=l(fR)=lr(ct)⊆lr(c)⊆lr(I)=I,whence ct∈ctI. Thus ct=ctramfor some r∈R.Let n=mt.Then

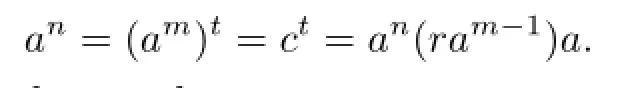
We prove that R is generalized π-regular.

(3)⇒(1).Let b∈N1(R)as above.Then bR is projective because R is weakly p.p.So bR is isomorphic to a summand of RR.Since R is a right C2 ring,it follows that bR is a summand of RR.Thus b is a regular element,and so N1(R)is regular.

Let 0̸=a∈R.Since R is a right weakly p.p.ring,there exists a positive integer n such that an̸=0 and anR is projective.So aRis isomorphic to a summand of RR.Since R is a right C2 ring,it follows that anR is a summand of RR.Thus a is a π-regular element,and so R is π-regular.By Lemma 4.1,R is regular.

(4)⇒(1).Similarly to the proof of[9,Theorem 3.6],we can prove that the left annihilator of a finitely generated proper right ideal is always nonzero.Since R is weakly p.p.,in view of [17,Theorem 5.4],N1(R)={0̸=a∈R|a2=0}is regular and R is generalized π-regular. Thus R is a regular ring by Lemma 4.1 again.

Remark 4.1 The conditions that R is right GP-injective or right C2 are not superfluous.

A ring R is said to be right(left)Kasch if every simple right(left)R-module embeds in RR.

Lemma 4.2 If R is a right weakly p.p.and left Kasch ring,then R is left weakly p.p.

Proof. Let 0̸=a∈R.By the right weakly p.p.hypothesis,there exists a positive integer n such that an̸=0 and r(an)=(1−e)R,where e2=e∈R.Then an=ane,and hence Ran⊆Re.Now we prove that Ran=Re.Otherwise,Ran⊆M,where M is a maximal submodule of Re.Since R is left Kasch,there exists a monomorphism f:Re/M →R by f(e+M)=b.Then eb=b and anb=0.So b∈r(an)=(1−e)R,and hence b=eb=0. Since f is monic,e∈M,contradicting with the maximality of M.So Ran=Re is projective, as desired.

Theorem 4.2 Let R be a ring.Then the following statements are equivalent:

(1)R is a semisimple Artinian ring;

(2)R is a right weakly p.p.and right Kasch ring;

(3)R is a right weakly p.p.and left Kasch ring.

Proof. (1)⇒(2)and(1)⇒(3)are clear.

(2)⇒(1)follows from[8,Theorem 3.8]and the fact that the right weakly p.p.rings are right PS.

(3)⇒(1).By Lemma 4.2,R is left weakly p.p.and left Kasch.Then the remainder of the proof is similar to that of(2)⇒(1).

[1]Cartain H,Eilenberg S.Homological Algebra.Princeton:Princeton University Press,1956.

[2]Kaplansky I.Rings of Operators.Math.Lecture Notes Series.New York:Springer,1965.

[3]Lam T Y.Lectures on Modules and Rings.New York:Springer-Verlag,1999.

[4]Hirano Y,Hongan M,ˆOhori M.On right p.p.rings.Math.J.Okayama Univ.,1982,24: 99–109.

[5]Huh C,Kim H K,Lee Y.p.p.rings and generalized p.p.rings.J.Pure Appl.Algebra,2002, 167:37–52.

[6]Lee Y,Huh C.Counterexamples on P.P.-rings.Kyungpook Math.J.,1998,38(2):421–427.

[7]Liu Z K,Zhao R Y.A generalization of pp-rings and p.q.-Baer rings.Glasg.Math.J.,2006, 48:217–229.

[8]Mao L X,Ding N Q,Tong W T.New characterizations and generalizations of pp rings.Vietnam J.Math.,2005,33:97–110.

[9]Mao L X.Generalized P-flatness and P-injectivity of modules.Hacet.J.Math.Stat.,2011, 40:27–40.

[10]Nicholson W K,Watters J F.Rings with projective socle.Proc.Amer.Math.Soc.,1988, 102(3):443–450.

[11]ˆOhori M.On non-commutative generalized p.p.rings.Math.J.Okayama Univ.,1984,26: 157–167.

[12]Yi Z,Zhou Y Q.Baer and quasi-Baer properties of group rings.J.Aust.Math.Soc.,2007, 83(2):285–296.

[13]Nam S B,Kim N K,Kim J Y.On simple GP-injective modules.Comm.Algebra,1995,23: 5437–5444.

[14]Yue Chi Ming R.On regular rings and self-injective rings.II.Glas.Mat.Ser.III,1983,18(2): 221–229.

[15]Chen J L,Zhou Y Q.GP-injective rings need not be P-injective.Comm.Algebra,2005,33: 2395–2402.

[16]Bass H.Finitistic dimension and a homological generalization of semiprimary rings.Trans. Amer.Math.Soc.,1960,95:466–488.

[17]Chen J L,Ding N Q.On the regularity of rings.Algebra Colloq.,2001,8:267–274.

A

1674-5647(2015)04-0362-11

10.13447/j.1674-5647.2015.04.08

Received date:Dec.24,2014.

The Scientific Research Foundation(12B101)of Hunan Provincial Education Department.

E-mail address:xymls999@126.com(Xiang Y M).

2010 MR subject classification:16D40,16E50