Co-commuting Mappings of Generalized Matrix Algebras

LIANG XIN-FENG AND XIAO ZHAN-KUI

(School of Mathematical Sciences,Huaqiao University,Quanzhou,Fujian,362021)

Communicated by Du Xian-kun

Co-commuting Mappings of Generalized Matrix Algebras

LIANG XIN-FENG AND XIAO ZHAN-KUI

(School of Mathematical Sciences,Huaqiao University,Quanzhou,Fujian,362021)

Communicated by Du Xian-kun

Let G be a generalized matrix algebra over a commutative ring R and Z(G)be the center of G.Suppose that F,T:G−→G are two co-commuting R-linear mappings,i.e.,F(x)x=xT(x)for all x∈G.In this note,we study the question of when co-commuting mappings on G are proper.

co-commuting map,generalized matrix algebra,proper

1 Introduction

Let R be a commutative ring with identity,A be a unital algebra over R and Z(A)be the center of A.Let us denote the commutator or the Lie product of the elements a,b∈A by [a,b]=ab−ba.Recall that an R-linear mapping f:A→A is said to be commuting if [f(a),a]=0 for all a∈A.A commuting mapping f of A is called proper if

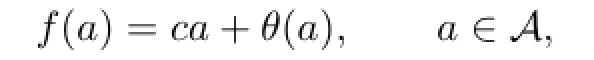
where c∈Z(A)and θ is an R-linear mapping from A to Z(A).As a generalization of commuting mappings,a pair of R-mappings F,T:A→A is said to be co-commuting if

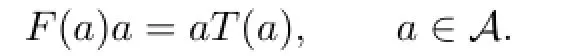
A pair of co-commuting mappings F,T is called proper if

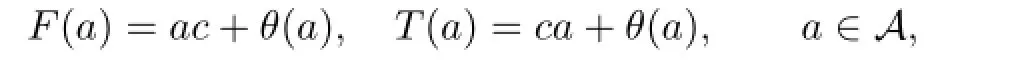
where c∈A and θ is an R-linear mapping from A to Z(A).

The usual goal when treating a commuting mapping is to describe its form.Generally,the form of commuting mappings can describe some structure information of algebras, especially,on the commutativity.The most important result on commuting mappings is Posner's theorem which states that the existence of a nonzero commuting derivation on aprime algebra A implies that A is commutative(see[1]).Breˇsar[2]showed that commuting mappings on prime algebras are proper.We encourage the reader to read the well-written survey paper(see[3]),in which the author presented the development of the theory of commuting mappings and their applications in detail.The following topics are discussed in[3]: commuting derivations,commuting additive mappings,commuting traces of multiadditive mappings,various generalizations of the notion of a commuting mapping,and applications of results on commuting mappings to different areas,in particular to Lie theory.These topics have formed the theory of functional identities,which deals with mappings of rings satisfying some identical relations(see[4–12]).

Let us recall the definition of generalized matrix algebras given by a Morita context.Let R be a commutative ring with identity.A Morita context consists of two R-algebras A and B,two bimodulesAMBandBNA,and two bimodule homomorphisms called the pairingssatisfying the following commutative diagrams:

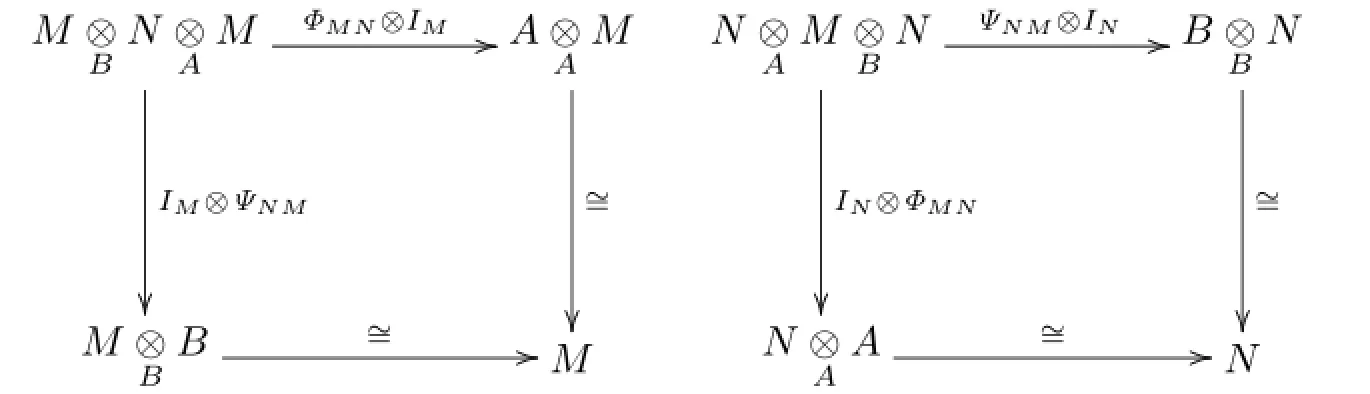
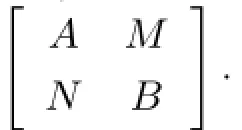
Cheung[15–16]initiated the study of commuting mappings of matrix algebras and determined the class of triangular algebras for which every commuting linear mapping is proper. Benkoviˇc and Eremita[17]studied commuting traces of bilinear mappings on triangular algebras,and gave the conditions under which every commuting trace of a triangular algebra is proper.This is applied to the study of Lie isomorphisms and of commutativity preserving mappings.Xiao and Wei[14]and their cooperators dealt with commuting mappings,semicentralizing mappings(see[18])on a generalized matrix algebra.Following their steps,we now study the question of when co-commuting mappings on a generalized matrix algebra G are proper.

2 Co-commuting Maps of Generalized Matrix Algebras

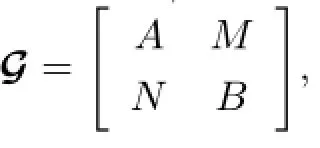
In order to give the main theorem,we especially hypothesis that N is faithful as a left B-module and also as a right A-module in the article.Let 1 and 1′be the identities of the algebras A and B.

It follows from Lemma 3.1 in[14]that the center Z(G)of G is

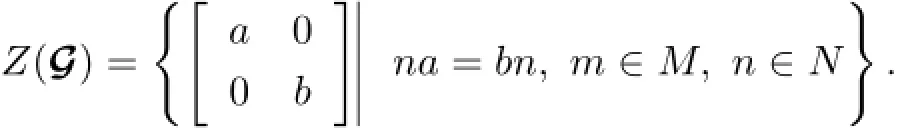
It is easy to see that πA(Z(G))is a subalgebra of Z(A)and πB(Z(G))is a subalgebra of Z(B).Furthermore,there exists a unique algebraic isomorphism(see Lemma 3.2 in[14]) φ:πA(Z(G))→πB(Z(G))such that

We are in position to state the main theorem of the article.

(1)πA(Z(G))=Z(A);

(2)πB(Z(G))=Z(B);

(3)there exist m0∈M and n0∈N,satisfying

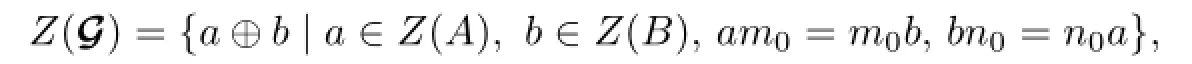
then every pair of co-commuting mappings F:G→G and T:G→G is proper.

For convenience let us denote A1=A,A2=M,A3=N,A4=B.Let

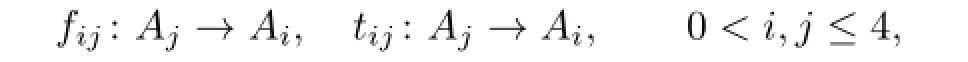
such that

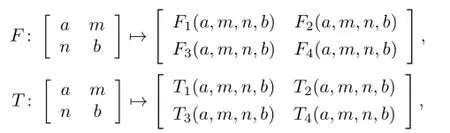
where

Since F and T is a pair of co-commuting maps,we have F(x)x=xT(x),i.e.,

Now we divide the proof of Theorem 2.1 into a series of lemmas for comfortable reading.

With the notations as above,we obtain Lemmas 2.1–2.9.

Lemma 2.1 For all a∈A1,m∈A2,n∈A3,b∈A4,

(1)F2(a,m,n,b)=f21(a)+f22(m),T2(a,m,n,b)=t22(m)+t24(b);

(2)f12(m)m=mt42(m),f13(n)m=mt43(n),f21(a)b=at24(b);

(3)at22(m)+mt41(a)=f11(a)m,f14(b)m+f22(m)b=mt44(b).

Proof. It follows from(2.1)that

Let us take a=0 and n=0 in(2.2).We can obtain that f12(m)m=mt42(m),f24(b)=0, and

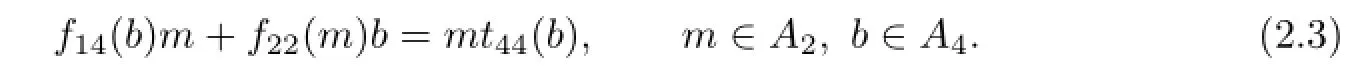
Choosing a=0 and m=0 in(2.2),we get f23(n)=0,for all n∈A3,b∈A4.Putting a=0 and b=0 in(2.2),we get f13(n)m=mt43(n)for all m∈A2,n∈A3.Setting m=0 and n=0 in(2.2),we obtain that f21(a)b=at24(b)and t21(a)=0.Denoting m=0 and b=0 in(2.2),we obtain that t23(n)=0.Taking n=0 and b=0 in(2.2),we have

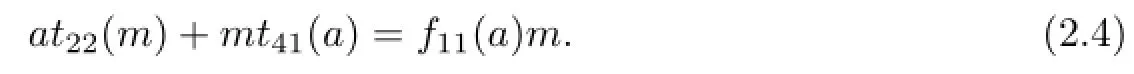
By the previous discussions,we can get that

for all a∈A1,m∈A2,n∈A3,b∈A4.

Lemma 2.2 For all a∈A1,m∈A2,n∈A3,b∈A4,

(1)F3(a,m,n,b)=f33(n)+f34(b),T3(a,m,n,b)=t31(a)+t33(b);

(2)f43(n)n=nt13(n),f42(m)n=nt12(m),f34(b)a=bt31(a);

(3)f33(n)a+f41(a)n=nt11(a),f44(b)n=nt14(b)+bt33(n).

Proof. It follows from(2.1)that

The rest proof is the same as the proof of Lemma 2.1,then we can obtain that Lemma 2.2 is true.

Lemma 2.3 For all a∈A1,m∈A2,n∈A3,b∈A4,

(1)f11(a)a=at11(a),f22(m)n=mt33(n);

(2)f13(n)a+f21(a)n=at13(n),f12(m)a=at12(m)+mt31(a);

(3)f14=t14:B→Z(A)is an R-linear mapping.

Proof. It follows from(2.1)that

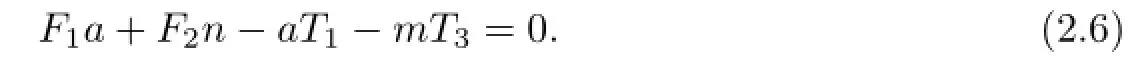
Taking a=0 and b=0 in(2.6),we get f22(m)n=mt33(n).Let us choose m=0 and n=0 in(2.6),we have

Set m=0 and b=0 in(2.6),we have

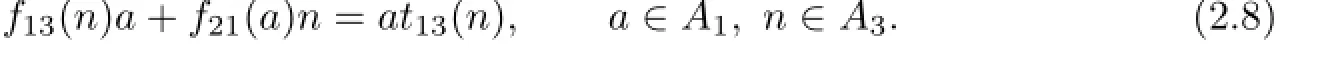
Putting n=0 and b=0 in(2.6),we obtain

Taking a=1 in(2.7),we can get f11(1)=t11(1)and f14(b)=t14(b).Furthermore, f14=t14:B→Z(A)is an R-linear mapping.

Lemma 2.4 For all m∈A2,n∈A3,b∈A4,

(1)f33(n)m=nt22(m),f44(b)b=bt44(b);

(2)f43(n)b=nt24(b)+bt43(n),f34(b)m+f42(m)b=bt42(m);

(3)f41=t41:A→Z(B)is an R-linear mapping.

Proof. It follows from(2.1)that

By a similar proof to that of Lemma 2.3,we know that Lemma 2.4 is correct.

Lemma 2.5 For all a∈A1,m∈A2,n∈A3,b∈A4,

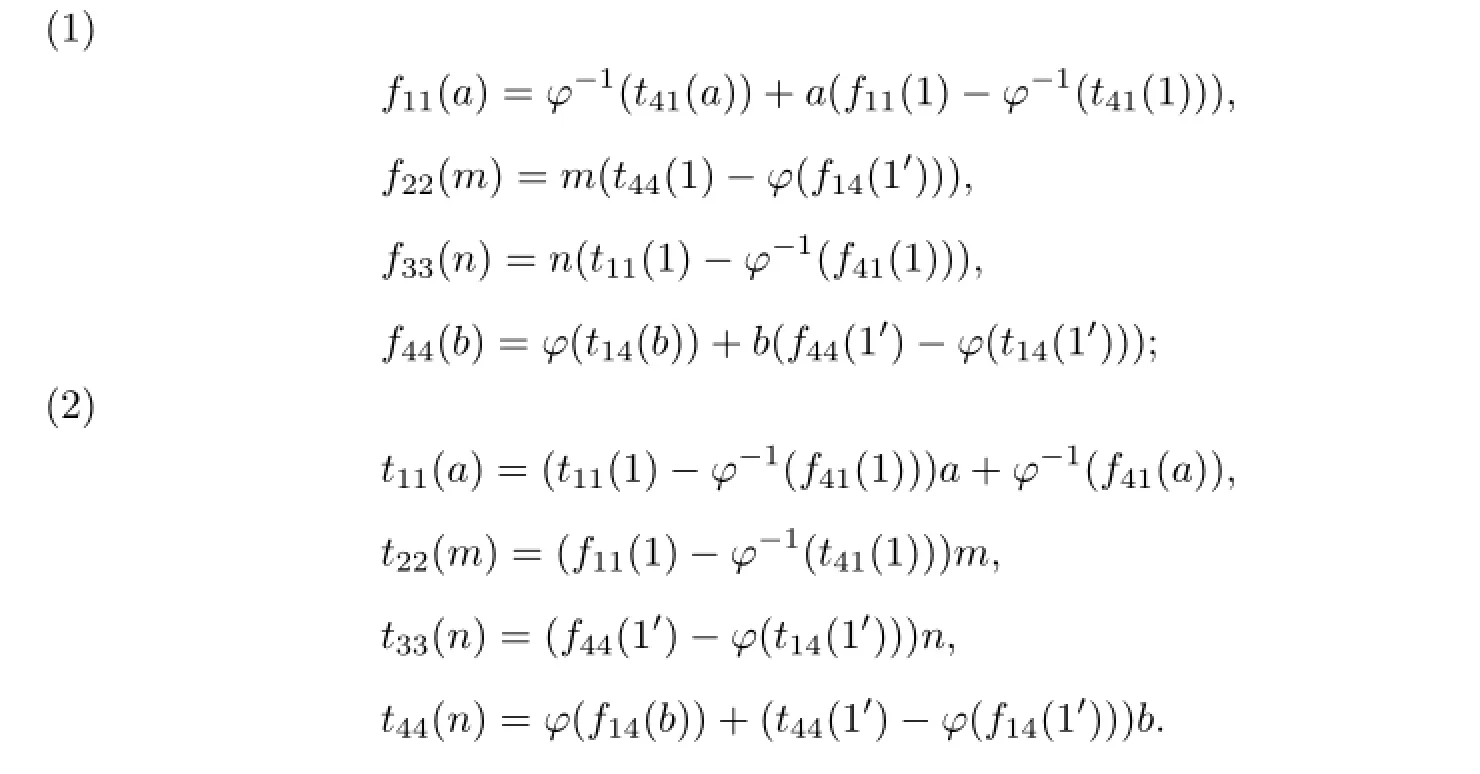
Proof. Letting a=1 in Lemma 2.2(3),we can get

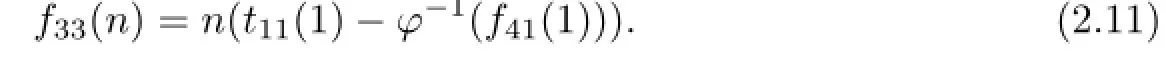
Furthermore,combining Lemma 2.2(3),(2.11)together with that N is faithful,we obtain that

Letting a=1 in(2.4),we have

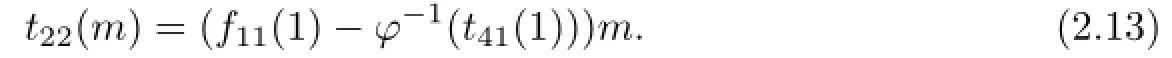
Furthermore,combining(2.4),(2.13)together with that M is faithful,we obtain

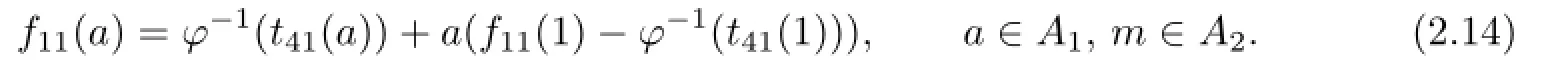
In the similar ways,letting b=1′in(2.3),we can obtain

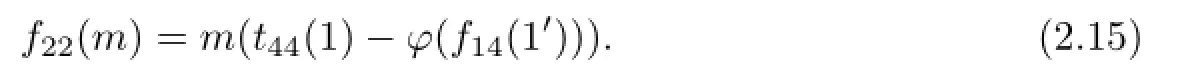
Furthermore,combining(2.3),(2.15)together with the faithfulness of M,we obtain that

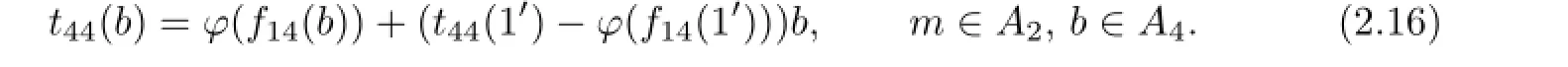
Letting b=1′in conclusion of Lemma 2.2(3),we can get

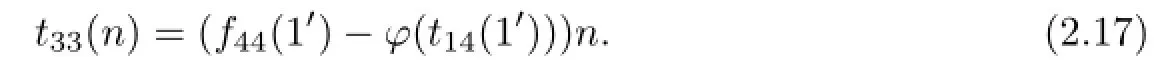
Furthermore,combining Lemma 2.2(3),(2.17)together with the faithfulness of M,we obtain that

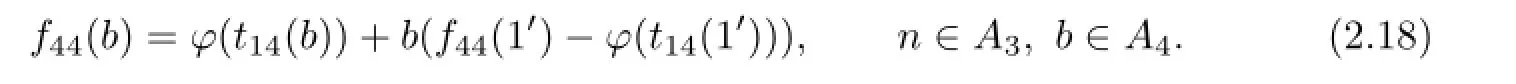
Lemma 2.6 For all a∈A1,n∈A3,b∈A4,

(1)f21(a)=at21(1),t24(b)=t24(1′)b;

(2)f13(n)⊕t43(n)∈Z(G).

Proof. Letting a=1,b=1′in f21(a)b=at24(b),and defining p=f21(1)=t24(1′)∈A2, we can obtain

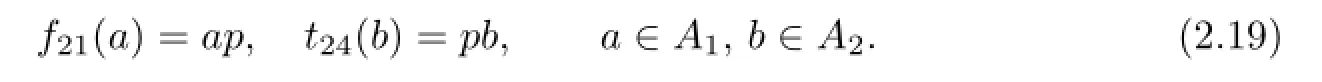
Supposing a=1 in(2.8),we can get

In the similar ways,establishing b=1′in(2)in Lemma 2.4,we can obtain that

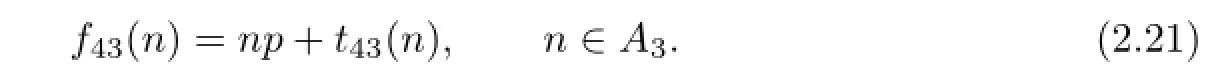
According to f43(n)n=nt13(n),combining(2.20)with(2.21),we can obtain that t43(n)n=nf13(n)for all n∈A3.There exist non-zero numbers m=m0,n=n0satisfying t43(n0)n0=n0f13(n0)and f13(n0)m0=m0t43(n0).So we can get f13(n0)⊕t43(n0)∈Z(G) due to the hypothesis of Theorem 2.1(3).

Replacing n by n+n0in t43(n)n=nf13(n),we get

and

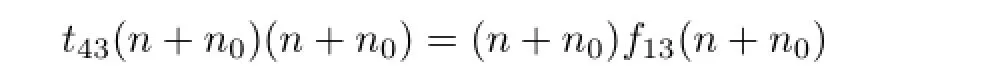
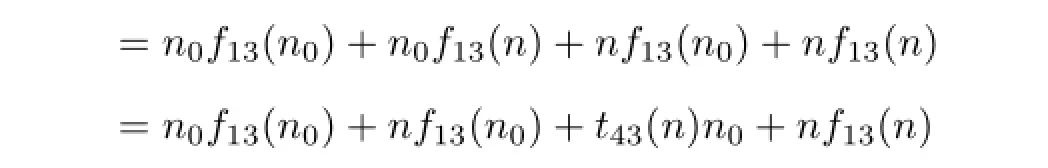
for all n∈A3.Combining the above two relations gives t43(n)n0=n0f13(n).Combining the resulting relation with f13(n)m0=m0t43(n),we can get

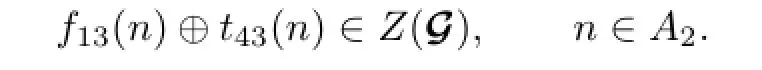
With the aid of(2.8)and(2.20),we can obtain

So we can get f21(a)=af21(1)because of the faithfulness of A3.

Combining Lemma 2.4(2)with(2.21),we can obtain

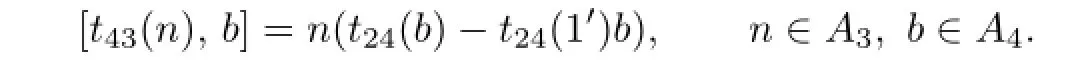
Then we can get t24(b)=t24(1′)b because A3is faithful for all b∈A4.

Proof. Combining f13(n)m=mt43(n)together with(2.20)and(2.21),we can get

Setting m=p=:m0in the above formula,we can obtain m0f43(n)=t13(n)m0.There exist non-zero numbers n=n0and m=m0satisfying

Then we obtain that f43(n0)⊕t13(n0)∈Z(G)because of the hypothesis of Theorem 2.1(3).

We can obtain that f43(n)n0=n0t13(n)from f43(n)n=nt13(n),using the similar ways of the proof of Lemma 2.6.Letting m=m0in mf43(n)=t13(n)m,and combining with f43(n)n0=n0t13(n),we can obtain that t43(n)⊕f13(n)∈Z(G)for all n∈A4.

Lemma 2.8 With the notations as above,we have

(1)there exists an s∈A3satisfying f34(b)=bs,t31(a)=sa;

(2)t12(m)⊕f42(m)∈Z(G)for all m∈A2,b∈A4.

Proof. Let a=1,b=1′in f34(b)a=bt31(a).Defining s=f34(1′)=t31(1)∈A3,we can get

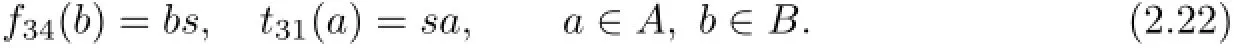
Setting a=1 in(2.9),we have

It follows that

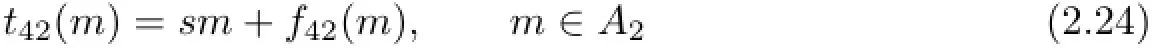
from setting a=1 in Lemma(2.4)(2).

According to f12(m)m=mt42(m),combining(2.23)with(2.24),we can obtain that t12(m)m=mf42(m)for all m∈A2.

There exist non-zero numbers m=m0∈A2,n=n0∈A2satisfying that

i.e.,

The rest steps are similar to the proof of Lemma 2.6.So we can get that(1)is correct.

Combining(2)in Lemma 2.4 with(2.24),we can get

Furthermore,f34(b)=bf34(1′),because of the faithfulness of M for all b∈A4.

Lemma 2.9 (1)f12(m)⊕t42(m)∈Z(G);

(2)t31(a)=t31(1)a for all a∈A1,m∈A2.

Proof.By using f42(m)n=nt12(m),(2.23)and(2.24),we have

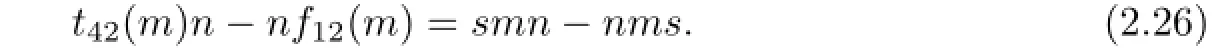
There exist non-zero numbers n=s=:n0,m=m0∈M in(2.26).Then we have t42(m0)n0=n0f12(m0).

On the other hand,letting n=s=n0,m=m0in mt42(m)=f12(m)m,thus we obtain that f12(m0)⊕t42(m0)∈Z(G).The rest steps is the same as the proof of Lemma 2.7,we obtain that f12(m)⊕t42(m)∈Z(G)for all m∈A2.

Due to(2.9)and(2.23),we can get

Combining(2.27)together with f12(m)⊕t42(m)∈Z(G)yields

because of the faithfulness of M for all a∈A1.

Proof of Theorem 2.1 Define

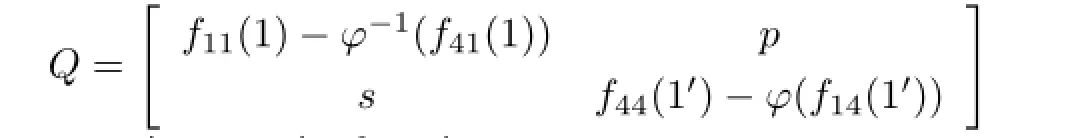
and for all a∈A1,m∈A2,n∈A3,b∈A4,

Combining Lemma 2.6(1)with Lemma 2.8(2),we can getµ:G→ Z(G).Combining Lemma 2.5(1),(2.19),(2.21)–(2.23)together with Lemma 2.8(2),yields

In the similar ways,combining Lemma 2.5(2),(2.20)–(2.22),(2.24)together with(2.28), yields

By the previous discussion,we get

This is the end of the proof of Theorem 2.1.

It is nature that we obtain the Corollaries 2.1 and 2.2.

(1)πA(Z(T))=Z(A);

(2)πB(Z(T))=Z(B);

(3)if there exists an m0∈M satisfying

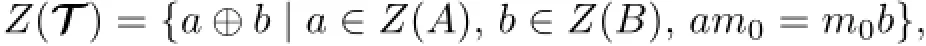
then every pair of co-commuting mappings F:T→T and G:T→T is proper.

Corollary 2.2 Let R be a commutative ring with identity and A be a unital algebra over R.Let Mn(A)(n≥2)be a full matrix algebra over A.Then every pair of co-commuting mappings F:Mn(A)→Mn(A)and G:Mn(A)→Mn(A)is proper.

[1]Posner E C.Derivations in prime rings.Proc.Amer.Math.Soc.,1957,8:1093–1100.

[2]Breˇsar M.Centralizing mappings and derivations in prime rings.J.Algebra,1993,156:385–394.

[3]Breˇsar M.Commuting maps:a survey.Taiwanese J.Math.,2004,8:361–397.

[4]Banning R,Mathieu M.Commutativity preserving mappings on semiprime rings.Comm. Algebra,1997,25:247–265.

[5]Breˇsar M.On a generalization of the notion of centralizing mappings.Proc.Amer.Math.Soc., 1992,114:641–649.

[6]Breˇsar M.Commuting traces of biadditive mappings,commutativity-preserving mappings and Lie mappings.Trans.Amer.Math.Soc.,1993,335:525–546.

[7]Breˇsar M,Chebotar M A,Martindale W S.Functional Identities,Frontiers in Mathematics. Basel:Birkh¨auser Verlag,2007.

[8]Krylov P A.Isomorphism of generalized matrix rings.Algebra Logic,2008,47:258–262.

[9]Lee P H,Wong T L,Lin J S,Wang R J.Commuting traces of multiadditive mappings.J. Algebra,1997,193:709–723.

[10]Marcoux L W,Sourour A R.Commutativity preserving maps and Lie automorphisms of triangular matrix algebras.Linear Algebra Appl.,1999,288:89–104.

[11]Mayne J H.Centralizing automorphisms of prime rings.Canad.Math.Bull.,1976,19:113–115.

[12]ˇSemrl P.Non-linear commutativity preserving maps.Acta Sci.Math.(Szeged),2005,71:781–819.

[13]Morita K.Duality for modules and its applications to the theory of rings with minimum condition.Sci.Rep.Tokyo Kyoiku Diagaku Sect.A,1958,6:83–142.

[14]Xiao Z K,Wei F.Commuting mappings of generalized matrix algebras.Linear Algebra Appl., 2010,433:2178–2197.

[15]Cheung W S.Commuting maps of triangular algebras.J.London Math.Soc.,2001,63:117–127.

[16]Cheung W S.Lie derivations of triangular algebras.Linear Multilinear Algebra,2003,51: 299–310.

[17]Benkoviˇc D,Eremita D.Commuting traces and commutativity preserving maps on triangular algebras.J.Algebra,2004,280:797–824.

[18]Li Y B,Wei F.Semi-centralizing maps of genralized matrix algebras.Linear Algebra Appl., 2012,436:1122–1153.

A

1674-5647(2015)04-0311-09

10.13447/j.1674-5647.2015.04.03

Received date:Jan.22,2014.

E-mail address:lxfrd@hqu.edu.cn(Liang X F).

2010 MR subject classification:16W20,15A78,47L35