Biquartic Finite Volume Element Method Based on Lobatto-Guass Structure

GAO YAN-NI AND CHEN YAN-LI

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Ma Fu-ming

Biquartic Finite Volume Element Method Based on Lobatto-Guass Structure

GAO YAN-NI AND CHEN YAN-LI

(School of Mathematics,Jilin University,Changchun,130012)

Communicated by Ma Fu-ming

In this paper,a biquartic finite volume element method based on Lobatto-Guass structure is presented for variable coefficient elliptic equation on rectangular partition.Not only the optimal H1and L2error estimates but also some superconvergent properties are available and could be proved for this method.The numerical results obtained by this finite volume element scheme confirm the validity of the theoretical analysis and the effectiveness of this method.

Lobatto-Guass structure,biquartic,finite volume element method,error estimate,superconvergence

1 Introduction

Finite volume element methods(FVEMs)(see[1–2]),also called generalized difference methods(see[3–6]),have been widely used in numerical partial differential equations and achieved great development,due to the local conservation property and other attractive properties such as flexibility in handling complicated domain geometries and boundary conditions.In essence,FVEMs and finite element methods(FEMs)both are methods based on interpolation.Since the finite volume element methods were proposed,it has been found that some properties valid for the finite element methods(see[7–8])are naturally valid for the finite volume element methods(see[3–6,9–12]).

The systematic theoretical analysis for FEMs with Lobatto-Guass structure has been attached much attention.Chen[7,13–14]discussed the super-convergence of the numerical solution and the numerical gradient for the one-dimensional two-point boundary problem.

When the finite element space takes order k,the numerical solutions and the numerical gradients for FEMs would have super-convergence at the zero points of Lobatto polynomials with order k+1 and at the k-th Guass points,respectively.In[7],these results are extended to higher dimensional elliptic problems for both rectangular and triangular meshes.By using unit orthogonal analysis,Chen[7]has proved all of the properties mentioned above.Motivated by the ideas of FEMs,people begin to apply the Lobatto-Guass structure to construct and discuss FVEMs in recent years.The works[16–18],respectively, analyze the first,the second and the third order FVEMs with Lobatto-Guass structure for one-dimensional two-points boundary problem.Therein not only the optimal H1-norm and L2-norm error estimates could be proved theoretically,but also the numerical solutions and the numerical gradients would have superconvergence at the primal partition's vertices and at dual partition's vertices,respectively.All above properties could be inherited for general optimal stress structure in[18].For the two-dimensional elliptic equations,the superconvergent biquadratic finite volume element method on rectangular meshes is discussed in[19]. Ciarlet[20]generalized the schemes mentioned in[19]to quadrilateral meshes,and obtained the optimal L2-norm error estimates.

If using the zeros of Lobatto polynomials to construct the Lagrange interpolation,then the corresponding optimal stress points(see[7,17])happen to be the Guass points.In this paper,we construct a biquartic finite volume element schemes on rectangular mesh by choosing the zeros of fifth-order Lobatto polynomials as primal partition's vertices and restricting the forth-order Guass points as the vertices of control volume,for two-order variable coefficient elliptic problems.The finite volume element schemes constructed by this way is proved to not only have o(h4)and o(h5)accuracy in H1-norm and L2-norm, respectively,but also have superconvergence for numerical gradients at the Guass points. In addition,we obtain a superconvergence for numerical solutions at the primal partition's vertices by numerical examples.

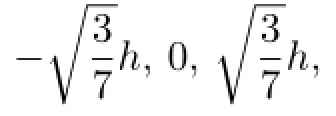
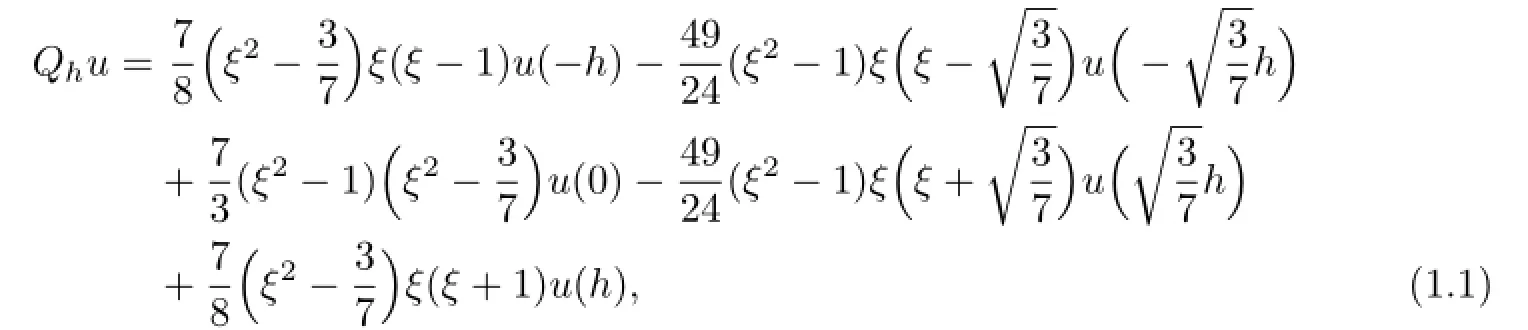
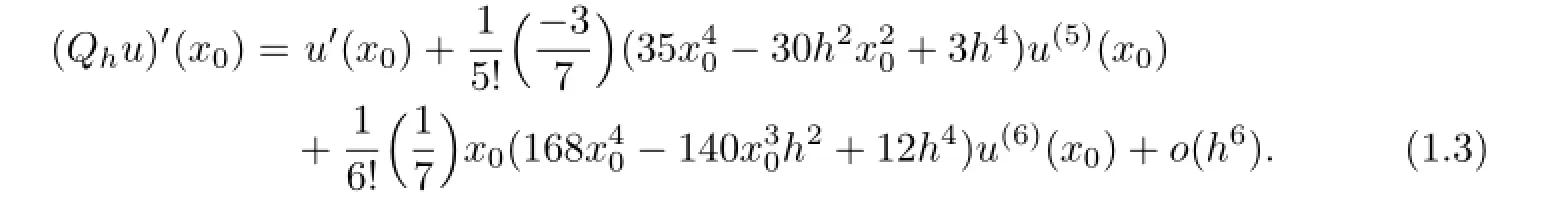
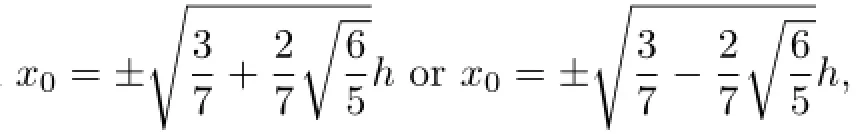
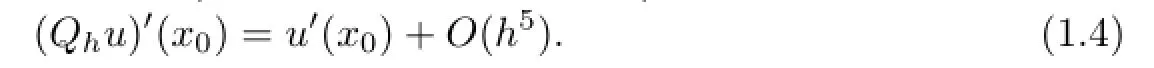
In the following,consider the interval[0,1],all above points can be responded onto[0,1].

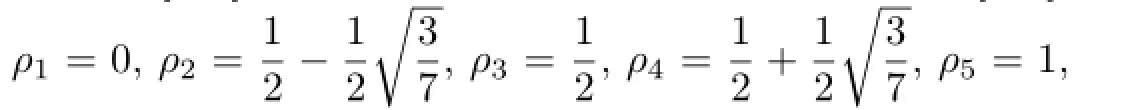
which are the Gauss points on[0,1].

In this case,denote by

the quartic basis functions in one dimension.

2 Biquartic FVEMs Based on Lobatto-Guass Structure

Consider the following two-order elliptic boundary problem:

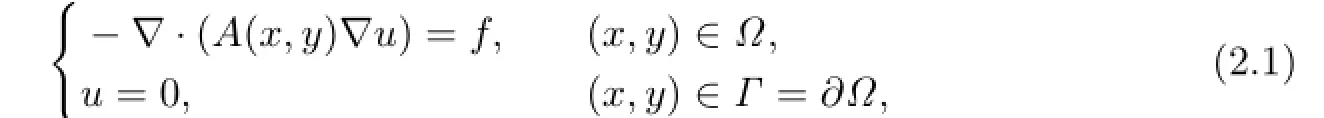
where Ω={(x,y)|a≤x≤b,c≤y≤d}is a rectangular whose boundary is Γ=∂Ω;is a given real diagonal matrix-valued function.Weassume that ai(x,y)are Lipschitz continuous and A is a uniformly positive definite matrix, i.e.,there exist two positive constants C1and C2,such that

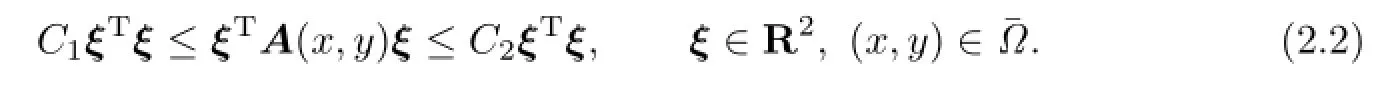
Throughout this paper,the definitions of Sobolev spaces and their norms,seminorms are the same as that presented in[20],C,C1,C2are used to denote positive constants independent of spacial step size and other relative parameters,which may be different in different places. Letwhere k,k1,k2are all positive integers.

We now expound the way how to construct the primal partition and the dual partition.

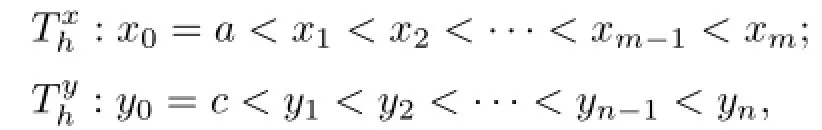
where m and n are two positive integers.The length of the intervalandis denoted byand,respectively.It is easy to knowForwe choose pointsas the interpolated nodes of biquartic finite element space,wherewithandThe set of all the interpolated points on Ω is denoted by Phandif removed the boundary points.Associated with the primal partition Th,we obtain its dual partitionby drawing two clusters of straight linesalong x-axis direction and y-axis direction,respectively,whereLetIn this article,we always suppose that This shape-regular,i.e., there exists a positive constant C such that

Next,we define the trial function space Uhand test function space Vh.Uhconsists of continuous functions on the closure of Ω,which vanishes on∂Ω and is a biquartic interpolated polynomial on each rectangularassociated with the dual partitionis defined as the set of all piecewise constants.More specifically,lebe the characteristic function of the dual elementThen

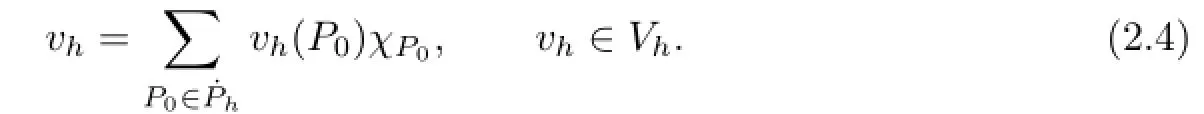
Note that a test function is identically zero at P0∈∂Ω.

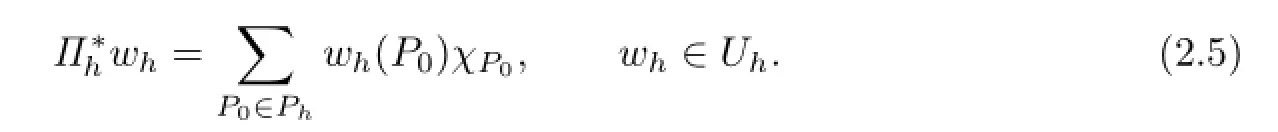
It is well known that Πhandsatisfy the following approximation properties:

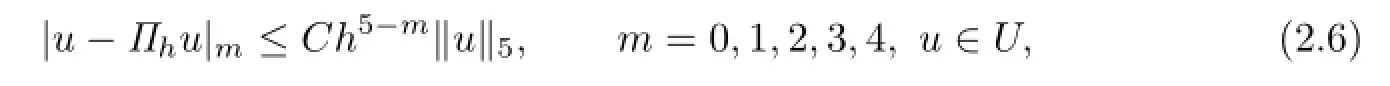
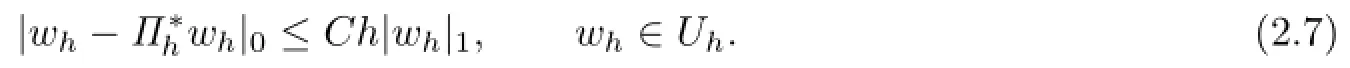
The biquartic FVEMs based on Lobatto-Guass structure for(2.1)is:find uh∈Uh,such that

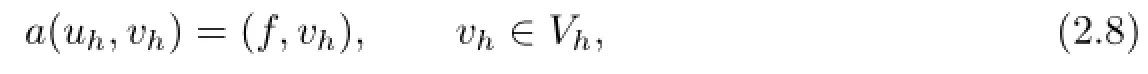
or equivalently

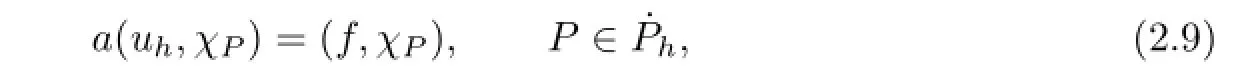
where

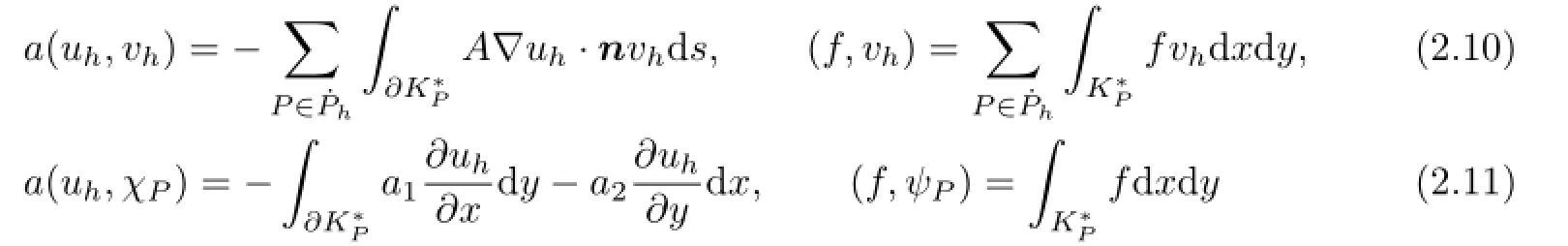
with n is the outward unit normal vector of

3 Priori Error Estimates

In this section,we first give a lemma describing the equivalence between discrete seminorm and continuous semi-norm.Futhermore,we derive two estimates for,which are extremely important in the demonstration of H1error estimate and superconvergent analysis,respectively.

First,we introduce some necessary notations.For elementTh,by virtue of the following linear transformation

the element Ki,jis mapped onto a reference elementMapping the interpolating nodesintoSuppose that uh∈Uhis a piecewise biquartic interpolating polynomial and letThen in the element Ki,j,uhcan be stated as follows:

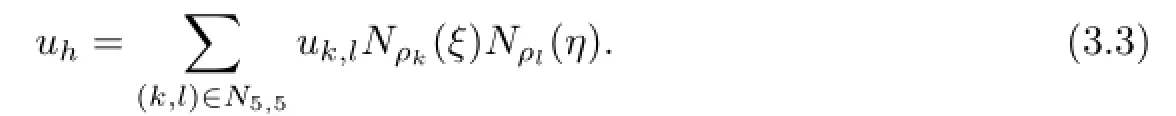
Hence,the partial derivatives of uhover Ki,jreads

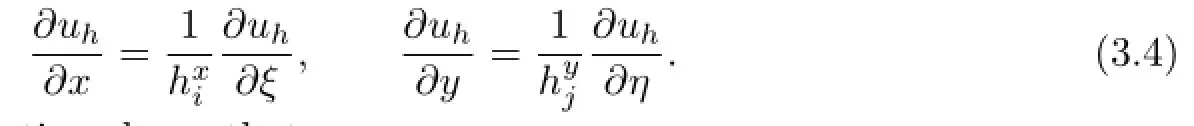
A straightforward computation shows that

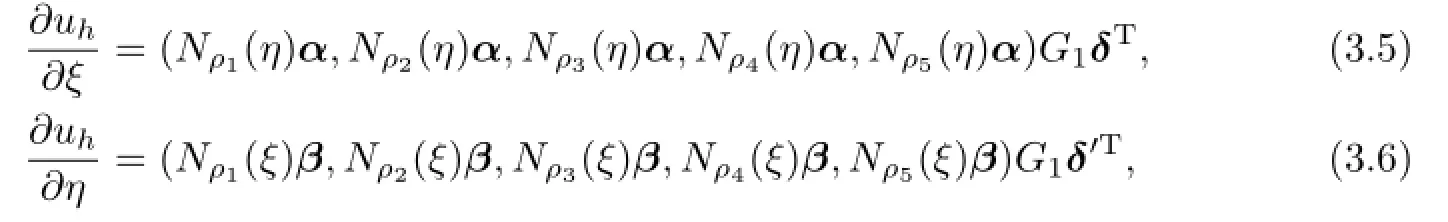
where

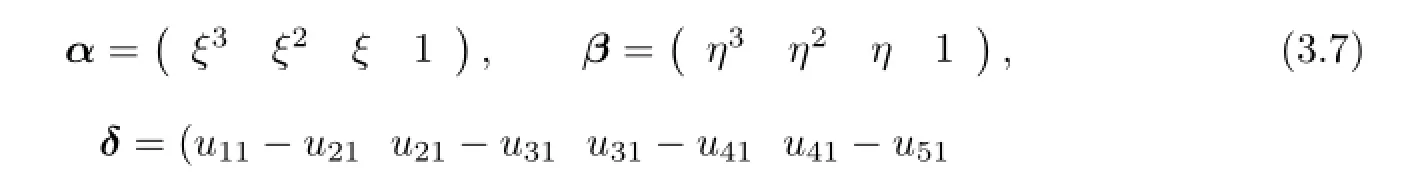
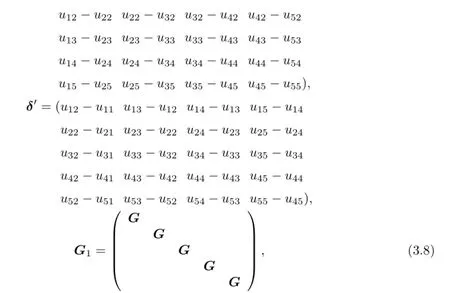
with G is a invertible matrix of order 4,only dependent of ρ1,ρ2,ρ3,ρ4and ρ5.We introduce the following discrete semi-norm|·|for Uh:

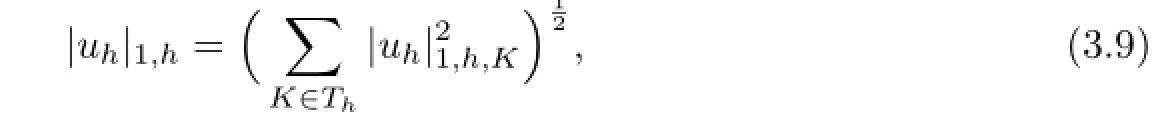
where

The following lemma gives the equivalence of the normal H1semi-norm and the discrete one.

Lemma 3.1 Assume that the partition Thsatisfies the conditions(2.3).Then for any uh∈Uh,|·|1,his equivalent to|·|1,i.e.,there exist positive constants C1and C2,such that

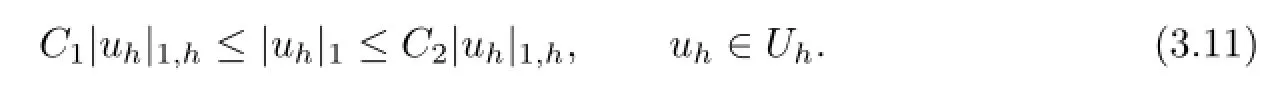
Proof. For arbitrary uh∈Uh,from the definition of|uh|1,we know

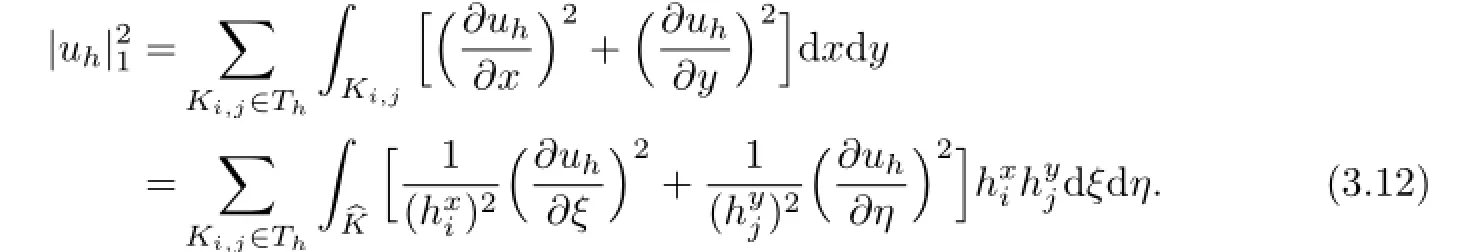
The following inequality can be held by the hypothesis(2.3),

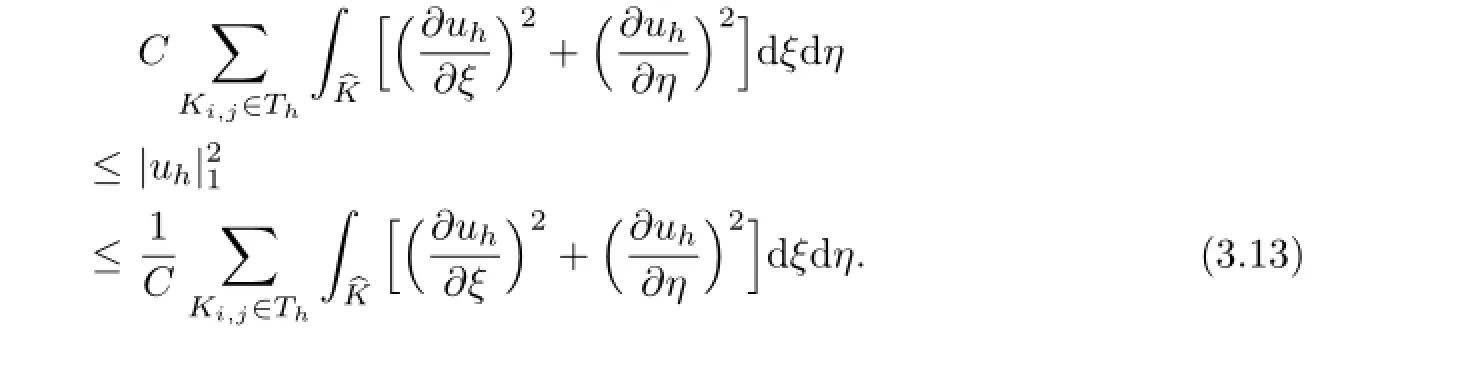
We can directly compute the integration,then we achieves

where A is a positive definite matrix.Because G1is invertiblestill keep positive definite.There obviously exist two positive constants λ1and λ2such that

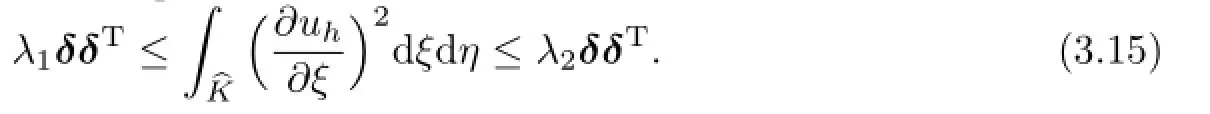
Finally,combining(3.13),(3.15)and(3.16),we obtain the desired inequality(3.11).

Theorem 3.1 Suppose that the partition This shape-regular.Then for sufficient small h,there exists a positive constant C such that

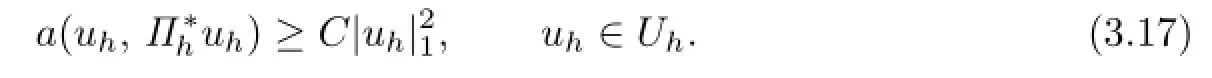
Proof. First,let e0=0,e5=1.Changing index in the summation,can be formulated into

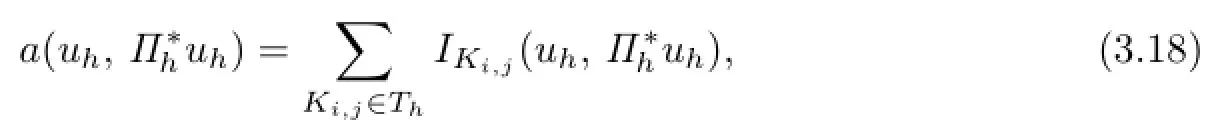
where

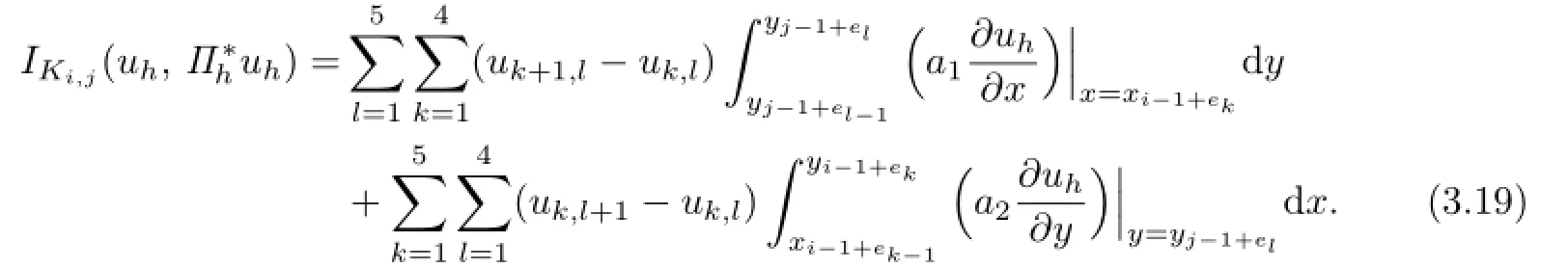
Next,turn ai(x,y)into a constant by fixing the value at point Q which is the center of Ki,j.We define

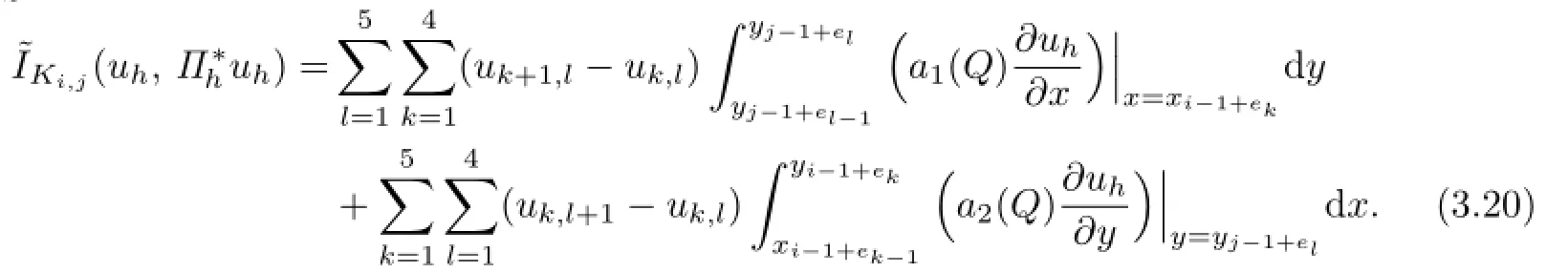
We need to estimate˜IKi,j.Through a direct computation,one yields that

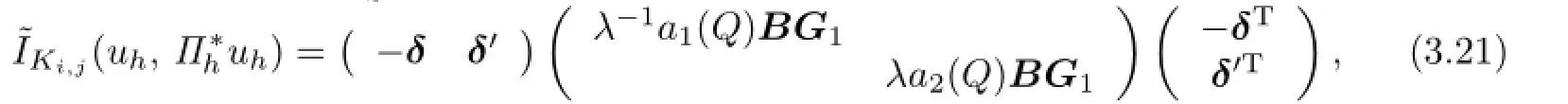
where

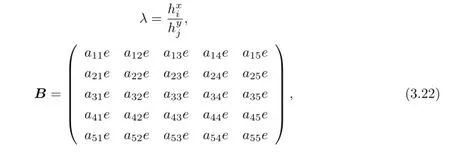
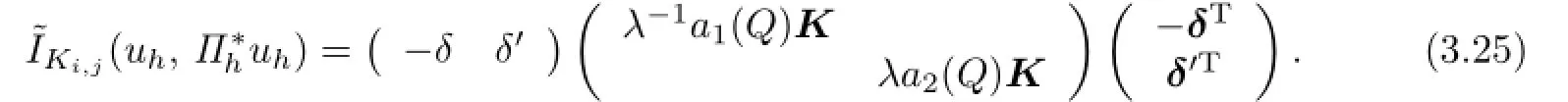
From the Lipschitz continuity of A(x,y),the Lemma 3.1,the trace theorem,Cauchy inequality and FEM inverse property,it yields that

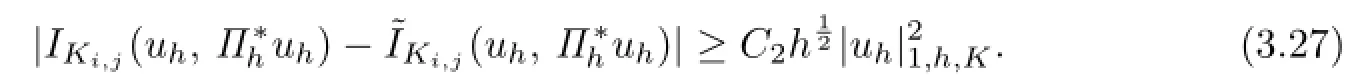
By virtue of the Poincar´e inequality,for sufficiently small h,one has

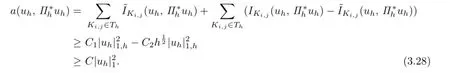
Theorem 3.2 Suppose that the partition This shape-regular.LetThen

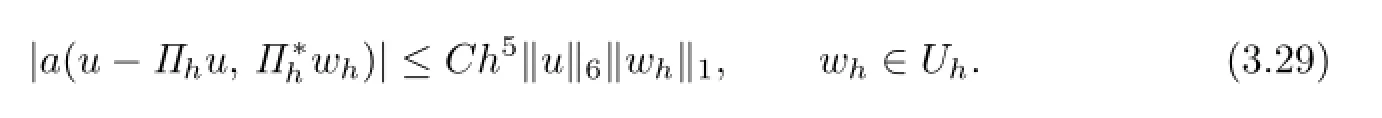
Proof. Analogous to the first part in the proof of Theorem 3.1,we have

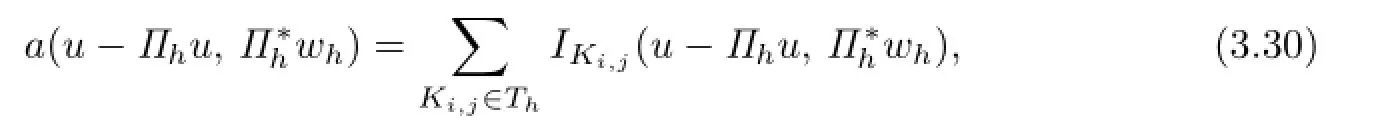
where

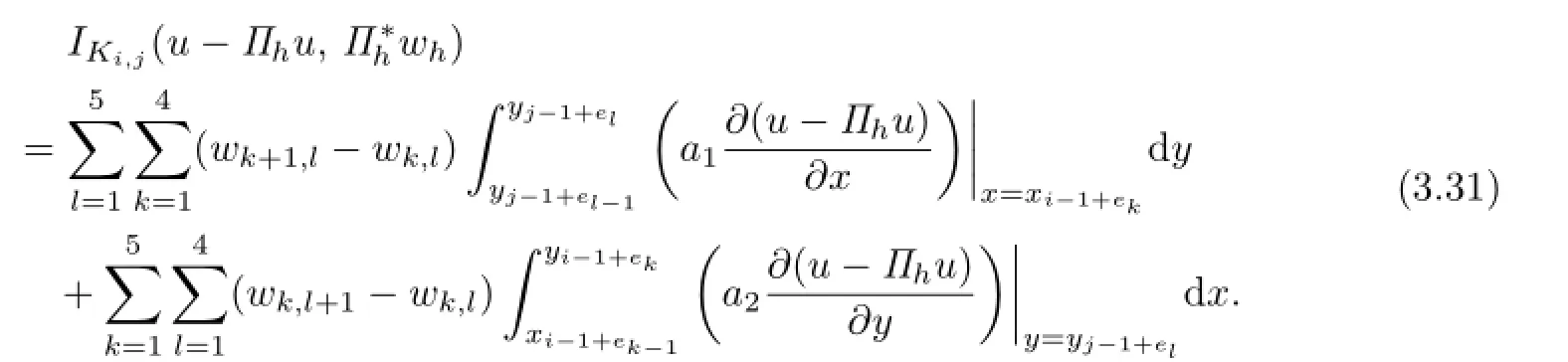
For(k,l)∈N4,5,let us consider

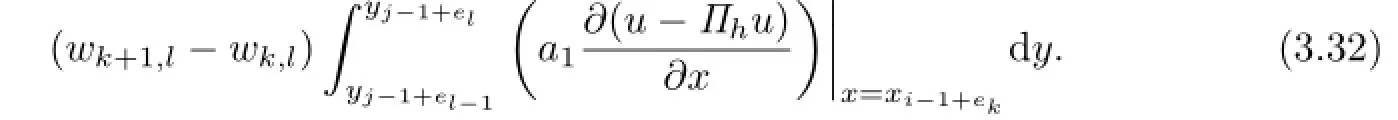
From the definition of|·|1,h,K,we obtain

From the linear transformations(3.1)and(3.2),it easy to know

Let

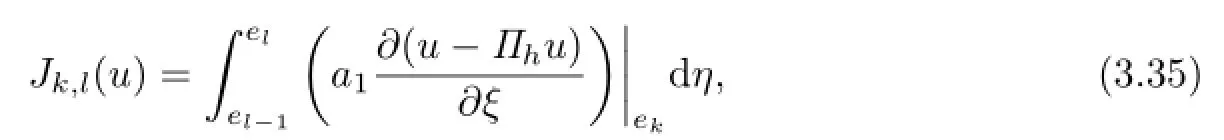
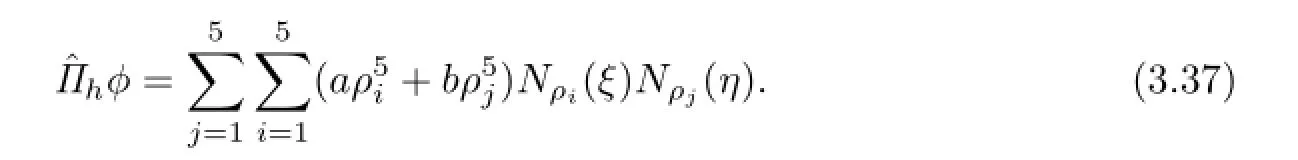
A straightforward calculation reveals that

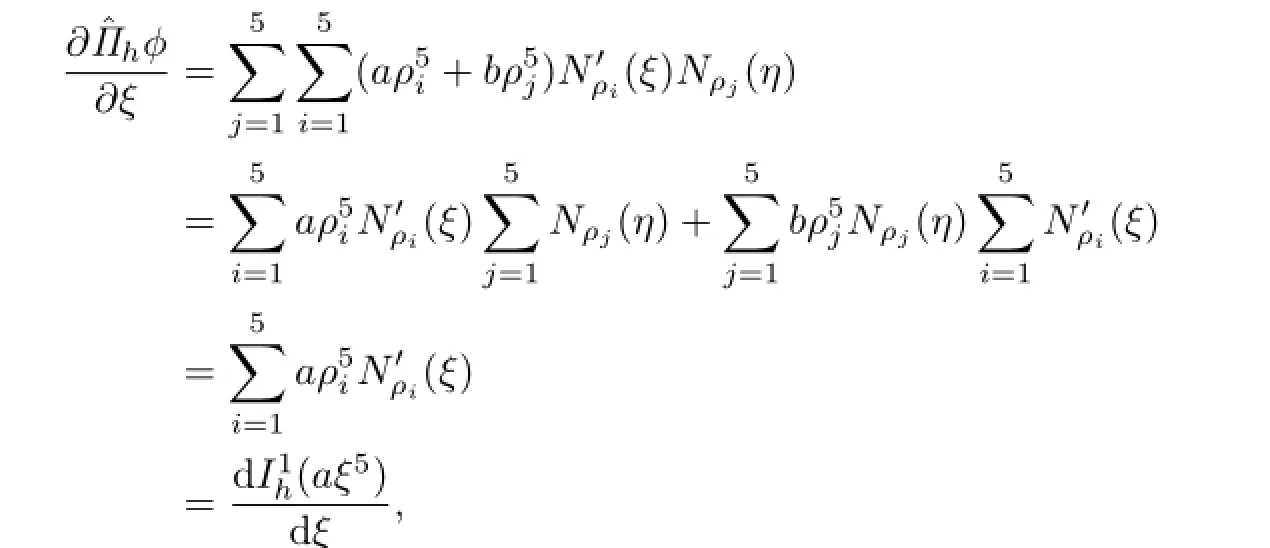
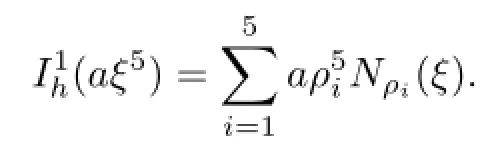
Then,we have

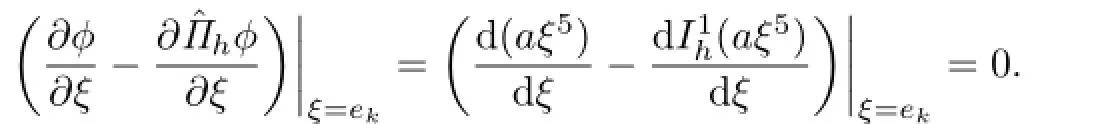
Therefore,

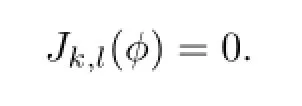
Combining with(3.36),we obtain

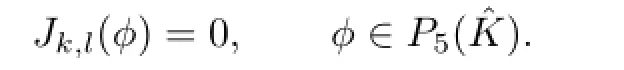
For any u∈H6(Ω),by Bramble-Hilbert Lemma,we have.By an integral transformation,it follows that

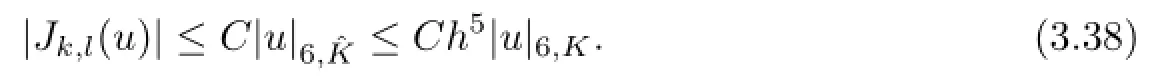
Combining(3.33)with(3.38),it suffices to arrive at

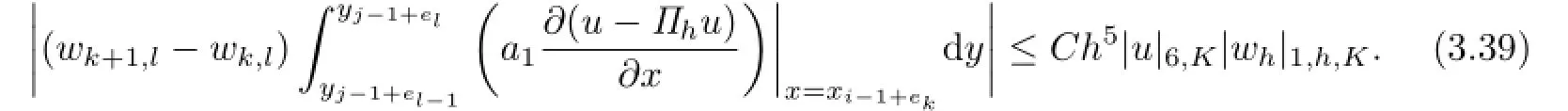
Similarly,for(k,l)∈N5,4,we can get

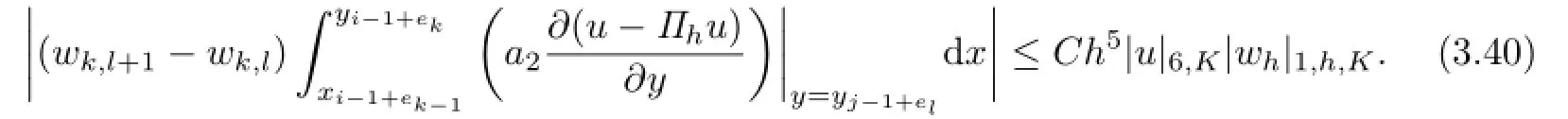
Substituting(3.39)and(3.40)into(3.31),and gathering over K,the proof can be completed by

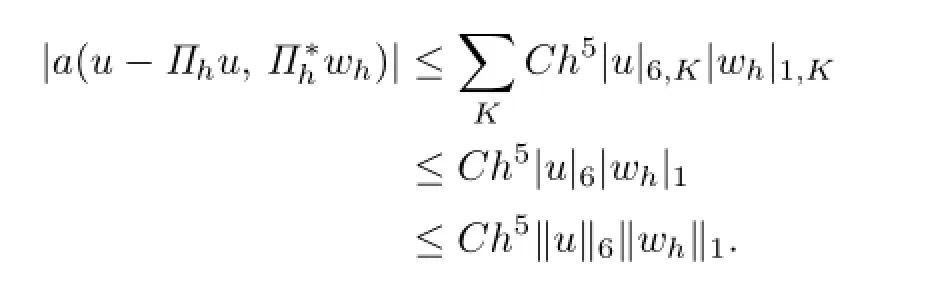
4 Error Estimates and Superconvergence

In this section,our aim is to derive the error estimates in the usual Sobolev norms and discuss the superconvergence for the numerical scheme(2.8).

The following orthogonality of awill be used in Theorem 4.2.Let(Ω)∩H6(Ω)be the solution of(2.1),and uh∈Uhbe the solution of the finite volume element scheme(2.8),we have

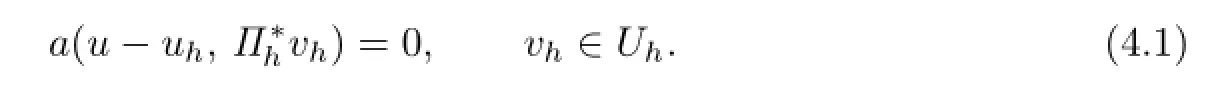
For the procedure of this proof,one can proceed similarly as Theorem 3.10 in[2].

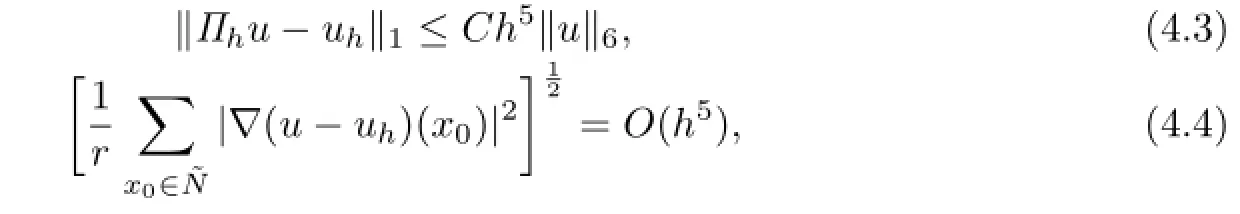
Proof. From Theorems 3.1,3.2 and 4.1,it suffices to get the following estimate:

So(4.3)is established.

On the one hand,by using the inverse property of FEM,it holds that

Note that r=O(h−2),and by(4.3),the following estimate holds:

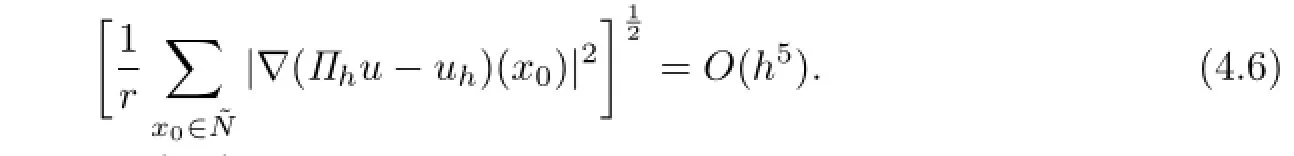
On the other hand,through(1.4)and a direct computation,we obtain that

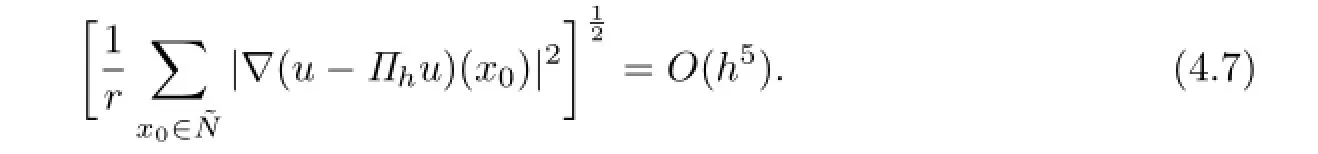
Combining the above two formulas,the desired result(4.4)is obtained.

Proof. From(2.6)and Theorem 4.2,we deduce that

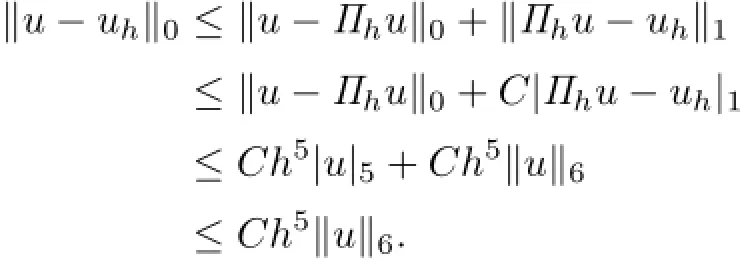
5 Numerical Experiments

In this section,we present some numerical results performed by several finite volume element schemes based on piecewise biquartic functions.We refer to the method(2.8)as Method I.

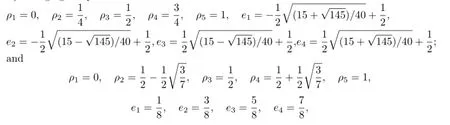
By changing the parameters aforementioned intothen the yielded finite volume element schemes are referred as Methods II and III,respectively.It needs to point out that the vertices of dual partition in Method II is still the optimal stress points of the interpolating polynomial.Our task is to verify the validity of theoretical analysis and compare numerically the convergence rate and the superconvergence of the three methods.To do this we consider the problem

where Ω=[0,1]×[0,1].Let u(x,y)=sin(3πx)sin(4πy)be the exact solution.The source term f(x,y)is determined by the above data.Then the methods are all performed on a uniform grid consisting of N×N square elements.For more details,see Tables 5.1–5.4.

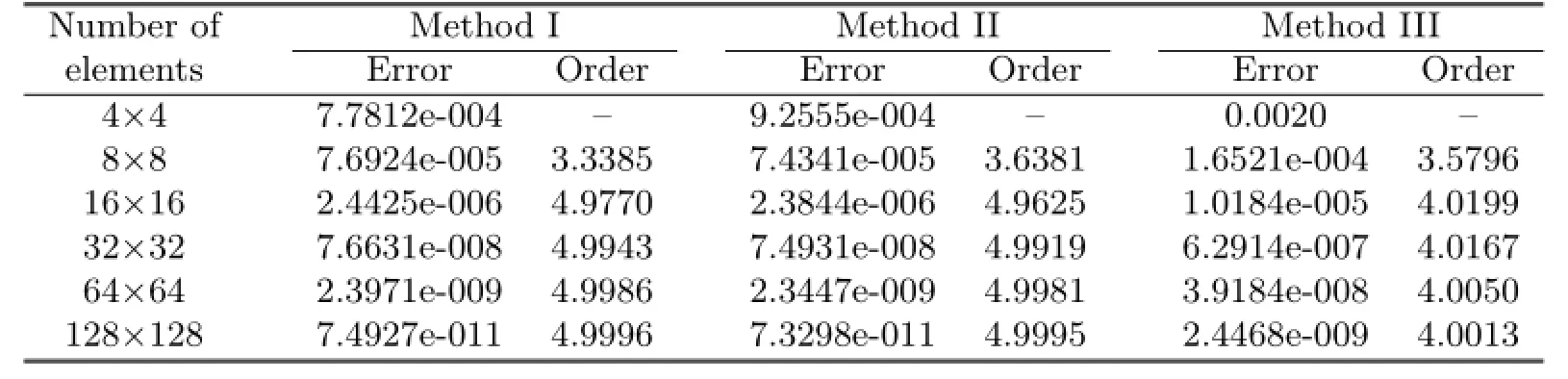
Table 5.1 Errors and convergence order of L2error estimate

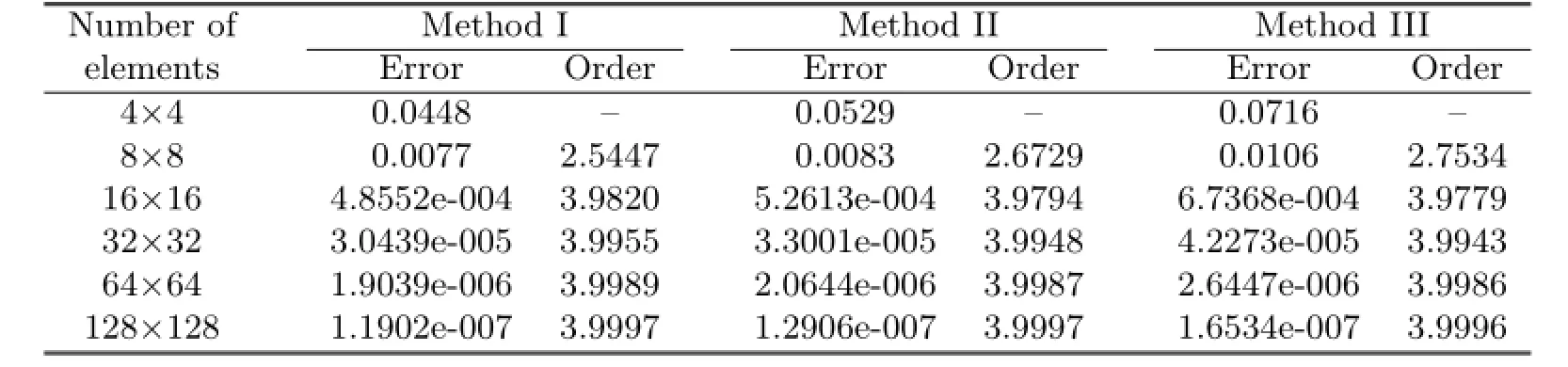
Table 5.2 Errors and convergence order of H1error estimate

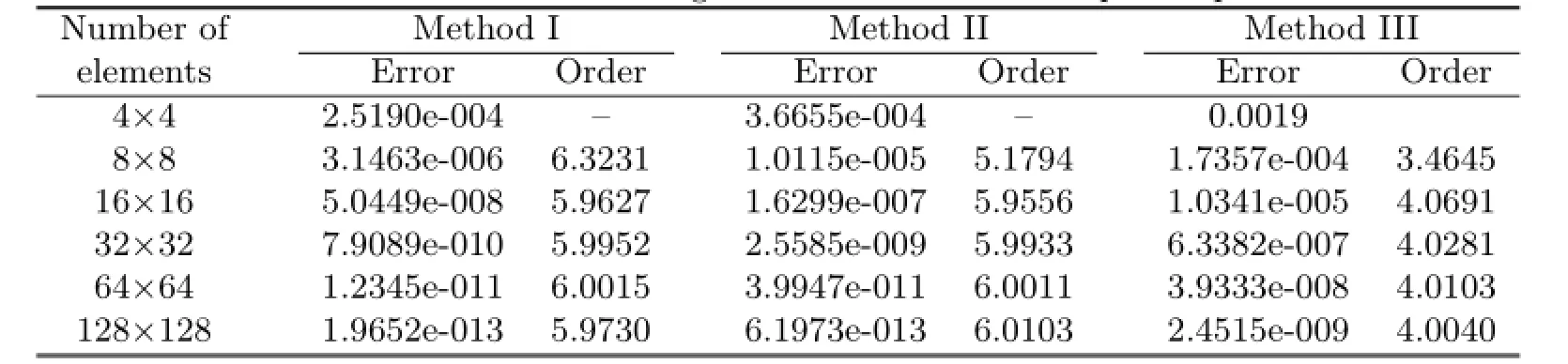
Table 5.3 Maximal errors and convergence orders of u−uhat primal partition's vertice

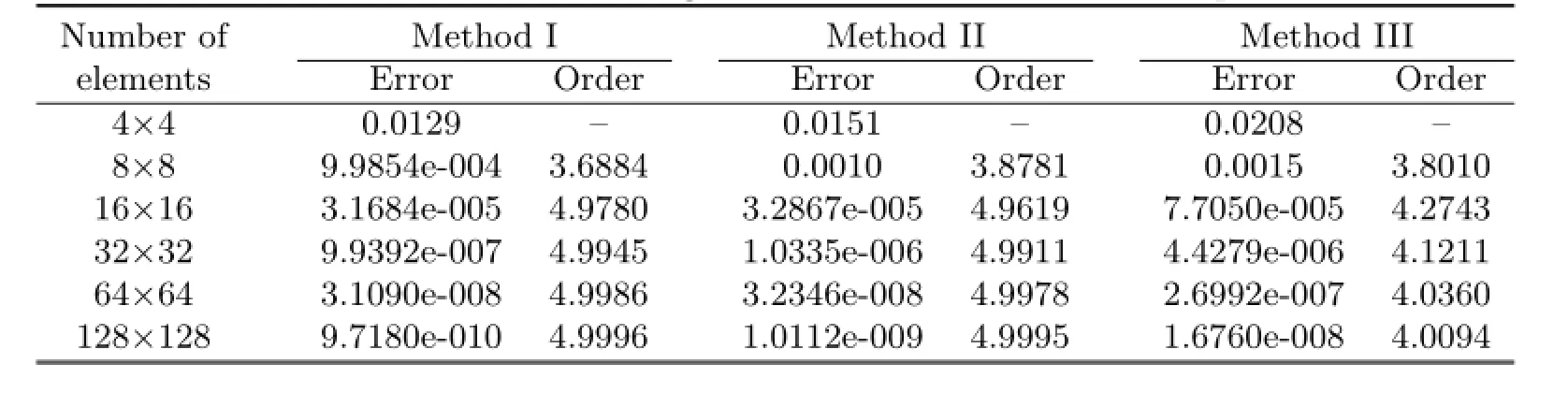
Table 5.4 Maximal errors and convergence orders of derivative at dual partition's vertice

From Tables 5.1–5.4,it can be noticed that Methods I and II have the same convergent rate,and the numerical results of Method I agree with the theoretical analysis.But if the way of dual partition is change,it can be seen from Method III that not only the convergent rate in L2-norm can not reach optimal,but also the superconvergent phenomenon would vanish.

[1]Cai Z Q.McCormick S.On the accuracy of the finite volume element method for diffusion equations on composite grid.SIAM J.Numer.Anal.,1990,27(3):636–655.

[2]Yang M.A second-order finite volume element method on quadrilateral meshes for elliptic equations.M2AN Math.Model.Numer.Anal.,2006,40(6):1053–1067.

[3]Li R H,Chen Z Y,Wu W.Generalized Difference Methods for Differential Equations Numerical Analysis of Finite Volume Methods.in:Monographs and Textbooks in Pure and Applied Mathematics.New York:Marcel Dekker Inc.,2000.

[4]Li Y H,Li R H.Generalized difference methods on arbitrary quadrilateral networks.J.Comput. Math.,1999,17:653–672.

[5]Chen Z Y.L2estimates of linear element generalized difference schemes.Acta Sci.Natur. Univ.Sunyaseni,1994,33(4):22–28.

[6]Zhu P,Li R.Generalized difference methods for second order elliptic partial fifferential equations(II)-quadrilateral grids.Numer.Math.J.Chinese Univ.,1982,4:360–375.

[7]Chen C M.Structure Theory of Superconvergence of Finite Element(in Chinese).Changsha: Hunan Science and Technology Press,2001.

[8]Brenner S C,Scott L R.The mathematical theory of finite element methods.2nd ed.in:Texts in Applied Mathematics.vol.15.New York:Springer-Verlag,2002.

[9]Richard E E,Lin T,Lin Y P.On the accuracy of finite volume element method based on piecewise linear polynomials.SIAM J.Numer.Anal.,2002,39:1865–1888.

[10]Wu H J,Li R H.Error Estimates for fnite volume element methods for general second order elliptic problem.Numer.Methods Partial Differential Equations,2003,19:693–708.

[11]Cai Z Q.On the finite volume element method.Numer.Math.1991,58:713–735.

[12]Lv J L,Li Y H.Optimal Biquadratic finite volume element methods on quadrilateral meshes. SIAM J.Numer.Anal.,2012,50(5):2379–2399.

[13]Chen C M.The good points of the approxiamation solution for Galerkin method for two-point boundary problem(in Chinese).Numer.Math.J.Chinese Univ.,1979,1(1):73–79.

[14]Chen C M.Superconvergence of finite element solutions and their derivatives(in Chinese). Numer.Math.J.Chinese Univ.,1981,3(2):118–125.

[15]Yu C H,Li Y H.Biquadratic element finite volume element method based on optimal stress points for solving Possion equation(in Chinese).Math.Numer.Sin.,2010,32(1):59–74.

[16]Sun J H,Qin D D,Yu C H.Quadratic finite volume element methods based on optimal stress points for solving one dimensional parabolic problems(in Chinese).J.Jilin Univ.Sci.,2011, 49(4):643–651.

[17]Yu C H,Wang X L,Li Y H.A class of modified cubic finite volume element method for solving two-point boundary value problems(in Chinese).Math.Numer.Sin.,2010,32(4):385–398.

[18]Gao G H,Wang T K.Cubic superconvergent finite volume element method for one-dimensional elliptic and parabolic equations.J.Comput.Appl.Math.,2010,233(9):2285–2301.

[19]Wang T K,Gu Y S.Superconvergent biquadratic finite volume element method for twodimensional Possion equations.J.Comput.Appl.Math.,2010,234(2):447–460.

[20]Ciarlet P G.The Finite Element Method for Elliptic Problems.Studies in Mathematics and its Applications.vol.4.Amsterdam-New York-Oxford:North-Holland Publishing Co.,1978.

A

1674-5647(2015)04-0320-13

10.13447/j.1674-5647.2015.04.04

Received date:April 29,2014.

The NSF(11371170)of China.

E-mail address:gaoyn10@mails.jlu.edu.cn(Gao Y N).

2010 MR subject classification:65M15