Lp-centroid Bodies and Its Characterizations
MA TONG-yI AND ZHANG DE-yAN
(College of Mathematics and Statistics,Hexi University,Zhangye,Gansu,734000)
Communicated by Rong Xiao-chun
Lp-centroid Bodies and Its Characterizations
MA TONG-yI AND ZHANG DE-yAN
(College of Mathematics and Statistics,Hexi University,Zhangye,Gansu,734000)
Communicated by Rong Xiao-chun
In this paper,we study the characteristic properties for Lp-centroid bodies,and an improved version of Busemann-Petty problem for Lp-centroid bodies is obtained.In addition,using the definitions of Lp-pole curvature image and Lp-affine surface area,a new proof of Busemann-Petty problem for Lp-centroid bodies is given.
convex body,star body,centroid body,Lp-centroid body,Busemann-Petty problem
1 Introduction
The concept of classic centroid body was first proposed by Blaschke and Dupin(see[1]), and was defined by Petty[2].Lutwak and Zhang[3]introduced the concept of Lp-centroid body.For each convex subset in Rn,it is well-known that there is a unique ellipsoid with the following property:The moment of inertia of the ellipsoid and the moment of inertia of the convex set are the same about every 1-dimensional subspace of Rn.This ellipsoid is called the Lengendre ellipsoid of the convex set.Namely,L2-centroid body Γ2K.The Lengendre ellipsoid and its polar(the Binet ellipsoid)are well-known concepts from classical mechanics.
As usual,V(K)denotes the n-dimensional volume of a body K in Euclidean space Rn. Let Sn−1denote the unit sphere in Rn.Let B denote the centered(centrally symmetric with respect to the origin)unit ball in Rn,and we write ωn=V(B)for its volume.
The definition of the classic centroid body was introduced by Petty[2]:Let K be a star body(about the origin)in Rn.Then the classic centroid body,ΓK,of K is the origin-symmetric convex body whose support function is given by
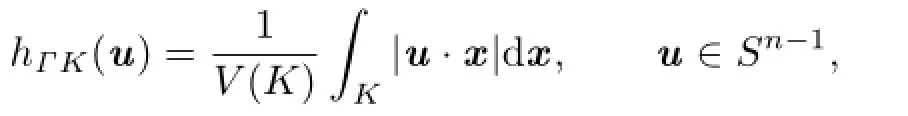
where x·y denotes the standard inner product of vectors x and y in Rn.
The classic centroid body is an important concept in convex geometry analysis.About the research of classic centroid body,Petty[4],Lutwak[5−7]and Zhang[8−10]have made plentiful and substantial achievements.
In 1997,Lutwak and Zhang[3]introduced the notion of Lp-centroid body,which extend the concept of the classical centroid body.Let K be a star body(about the origin)in Rnand p≥1.Then the Lp-centroid body,ΓpK,of K is the origin-symmetric convex body whose support function is given by
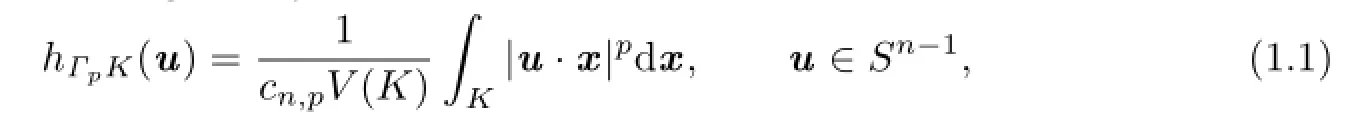
where
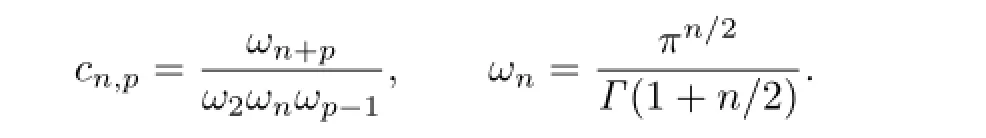
By using polar coordinate transformation in(1.1),we can obtain

For set of the palar bodies of all Lp-projection bodies,we define the following:
(ii)(Rn,||·||L)is isometric to a subspace of Lp.
The latter fact can be found in[11].
Concerning the operator Γp,a well-known Shephard problem can be stated as follows: Let K,L be two origin-symmetric convex bodies in Rnand suppose that,for every p≥1, ΓpK⊆ΓpL,does it follow that we have an inequality for the volumes of K and L?
The premier solution of this problem was given by Grinberg and Zhang[12].Their results are described as follows:
Theorem 1.1 Let K be a star body(about the origin)in Rn,L∈Π∗p,and p≥1.If ΓpK⊆ΓpL,then
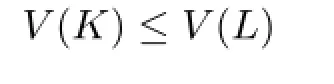
with equality for n̸=p≥1 if and only if K=L.
On the other hand,if K ̸∈Π∗
p,then there is a body L such that ΓpK ⊆ ΓpL,but V(K)>V(L).
In this paper,we further study the characteristic properties of Lp-centroid bodies.First, we give the following result for Lp-centroid bodies.
Theorem 1.2 Let K,L be two star bodies(about the origin)in Rnand p≥1.If p is not an even integer,then ΓpK=ΓpL if and only if

for any origin-symmetric star body Q in Rn.
Next,as the applications of Theorem 1.2,we have the following facts:
Theorem 1.3 Let K,L be two star bodies(about the origin)in Rnand p≥1.If p is not an even integer,then
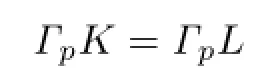
if and only if K and L are dilates.
The following theorem is a similar version of Theorem 1.1,called the Shephard problems of Lp-centroid bodies.
Theorem 1.4 Let K be a star body(about the origin)in Rn,L be an origin-symmetric star body in Rn,and p≥1.If p is not an even integer and ΓpK=ΓpL,then
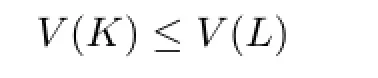
with equality if and only if K=L.
Finally,combining Lp-polar curvature images with Lp-affine surface area,we give a new proof of Theorem 1.1.
2 Preliminaries
2.1 Support Function,Radial Function and the Polar of Convex Body
If K is a convex body(compact,convex subsets with non-empty interiors)in Rn,then its support function,hK=h(K,·):Rn→(0,+∞),is defined by(see[1,13])
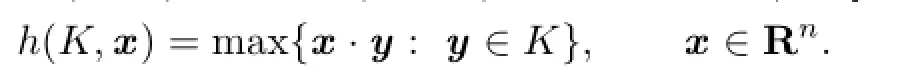
Let Kndenote the set of convex bodies in Rn.For the set of convex bodies containing origin in their interiors and the set of origin-symmetric convex bodies in Kn,we write asand,respectively.
If K is a compact star-shaped(about the origin)in Rn,its radial function,ρK=ρ(K,·): Rn{0}→[0,∞),is defined by(see[1,13])
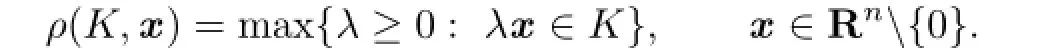
If ρKis positive and continuous,then K is called a star body(about the origin).Letdenote the set of all star bodies(about the origin)in Rn.For the set of origin-symmetric star bodies in,we write asTwo star bodies K and L are said to be dilates(of one another)if ρK(u)/ρL(u)is independent on u∈Sn−1.From the definition of the radial function of star body it follows that

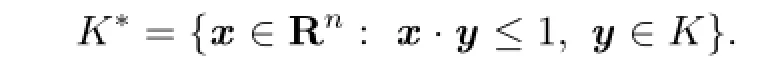
Obviously,we have(K∗)∗=K.In addition,the polar body of convex body has the following property:Ifthen(ϕK)∗=ϕ−tK∗.In particular,

From the definitions of the support and radial functions as well as the definition of the polar body,it follows that forand any u∈Sn−1,
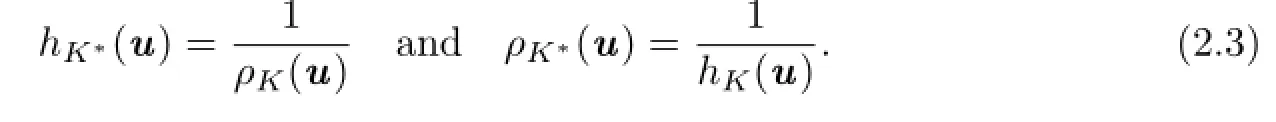
2.2 Dual Lp-mixed Volume and Dual Lp-surface Area
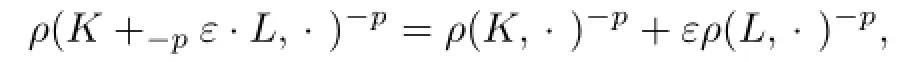
where“ε·L”is different from“ε·L”in Lp-Firey combination.
In 1996,Lutwak[16]defined the concept of dual Lp-mixed volume.For K,L∈Sno,p≥1 and ε>0,the dual Lp-mixed volume,of K and L is defined by
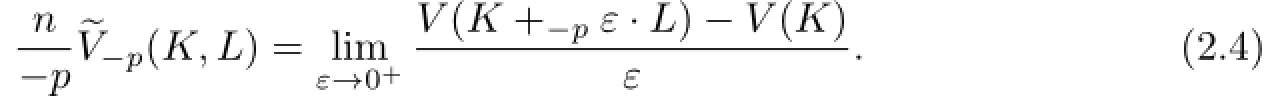
Further,Lutwak[16]showed the integral formula of dual Lp-mixed volume as follows:If K,then

Apparently,

By using H¨older's inequality,we easily prove the following Minkowski's inequality for dual Lp-mixed volume:If K,then

with equality if and only if K and L are dilates.
According to the definition of dual Lp-mixed volume,we put forward the concept of dual Lp-surface area.LetThen the dual Lp-surface area,of K is defined by

Together with(2.4),(2.5)and(2.7),the integral representation of dual Lp-surface areais obtained as follows:

In addition,we define the Borel measureon Sn−1,by

for each Borel ω⊂Sn−1.By(2.9)we can immediately get

2.3 Lp-projection Body
Lutwak et al.[17]posed the notion of Lp-projection body:For eachand p≥1,the Lp-projection body,ΠpK,of K is an origin-symmetric convex body whose support function is given by

where Sp(K,·)is a positive Borel measure on Sn−1,called the Lp-surface area measure of K.As usual,we denote byK the polar body of ΠpK.
In addition,the following result will be used in the proof of our main results.If p is not an even integer,andµis a signed finite even Borel measure,then
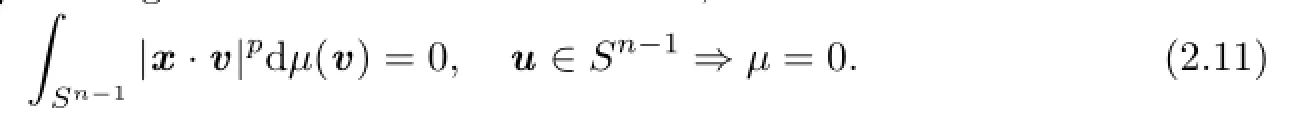
See,e.g.,[4,11,18–21].
2.4 Lp-curvature Function,Lp-affine Surface Area and Lp-polar Curvature Images
A convex body K ∈Knis said to have a curvature function f(K,·):Sn−1→R,if its surface area measure S(K,·)is absolutely continuous with respect to spherical Lebesgue measure S,and the Radon-Nikodym derivative is(see[16,22])
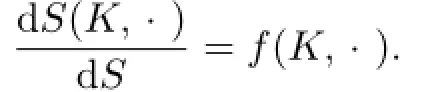
Let Fndenote the set of all convex bodies in Knthat has a positive continuous curvature function.Letdenote the sets of all convex bodies inrespectively,and both of them have a positive continuous curvature function.

Lutwak[16]introduced the concept of Lp-affine surface area as follows:For,the Lp-affine surface area,Ωp(K),of K is defined by

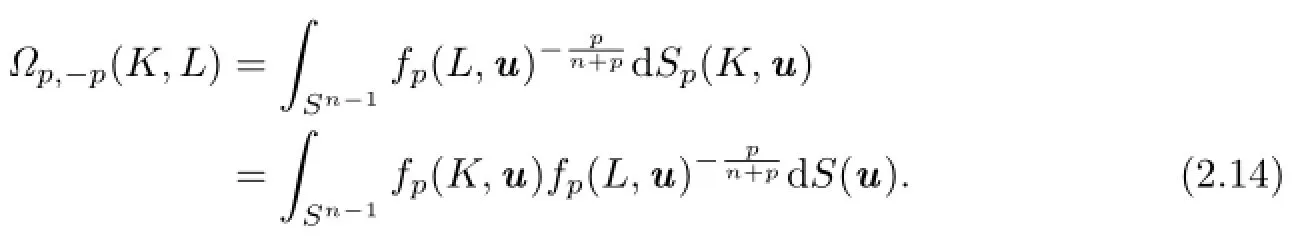
Together with(2.12),(2.13)and(2.14),it shows that for

In addition,using H¨older's inequality,it is easy to show that for K,
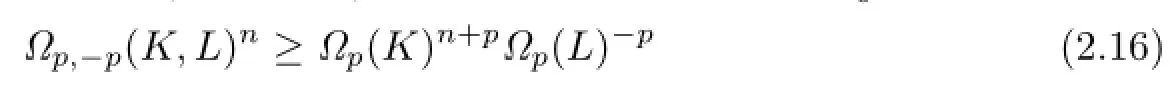
with equality in inequality(2.16)for n̸=p=1 if and only if K and L are homothetic,for n̸=p>1 if and only if K and L are dilates.
According to the concept of Lp-curvature image of convex body K,Zhu et al.[24]showed the notion of Lp-pole curvature image as follows:For eachand n̸=p≥1,definethe Lp-pole curvature image of K,by
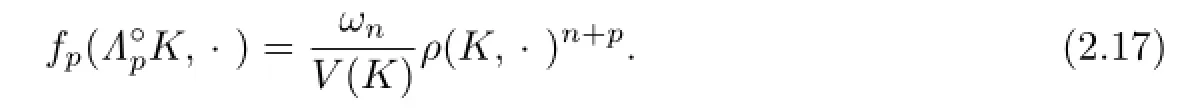
If p=1,(2.17)is defined by Lutwak(see[1]).
3 The Characteristic Properties of Lp-centroid Bodies
This section gives the characteristic properties of Lp-centroid bodies.We first complete the proof of Theorem 1.2.
Proof of Theorem 1.2 Because S(·)=S(B,·)is an even measure on Sn−1,S(−v)= S(v)for any v∈Sn−1.Thus,for,by the formula of n-dimensional volume of star body and(2.1),we have
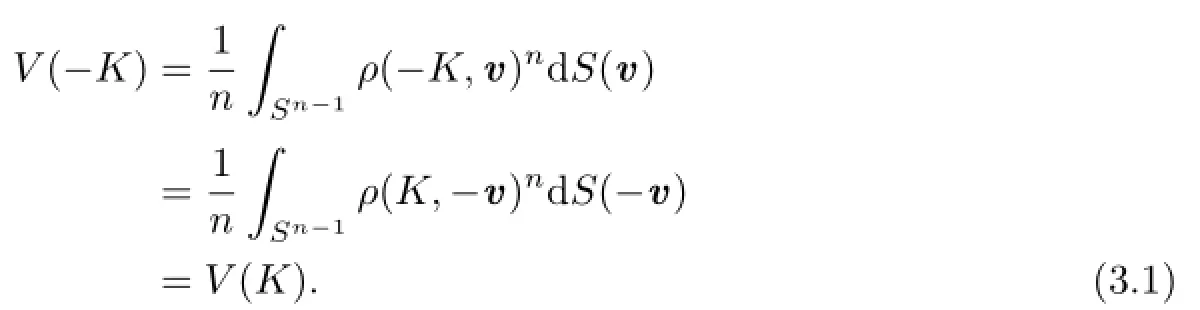
Therefore,by the definition(1.2)of Lp-centroid body,(2.1)and(3.1),for,we have

It follows that
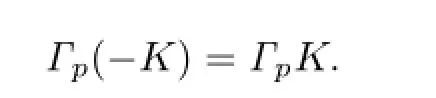
Together with(1.2),(2.10)and(3.1),it shows that
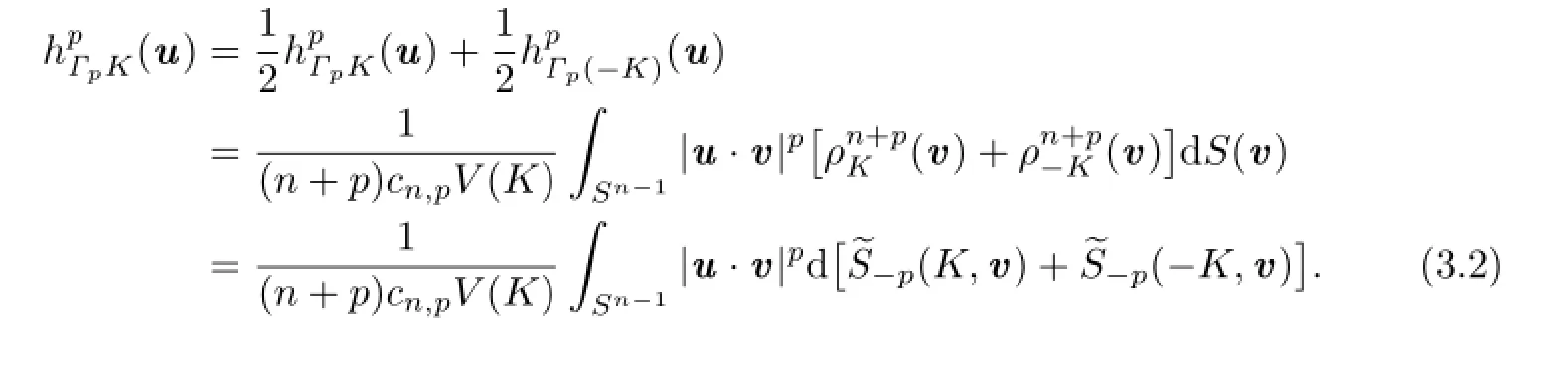
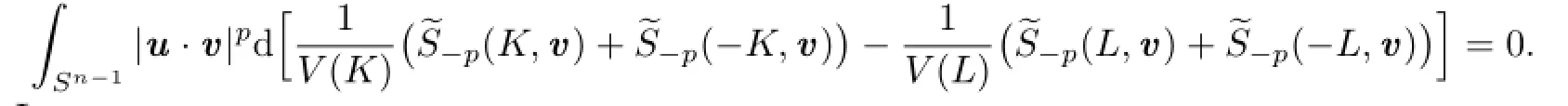
Let

It is easy to show thatµ(v)is an even measure on Sn−1.Therefore,from(2.11)we know that for all v∈Sn−1,µ(v)=0.Namely,
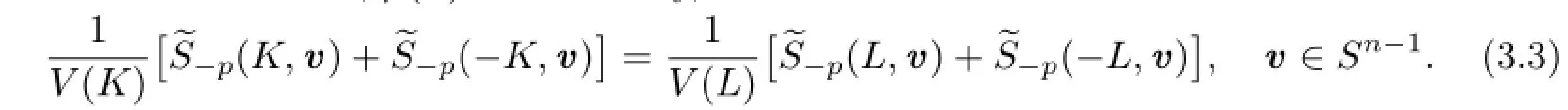

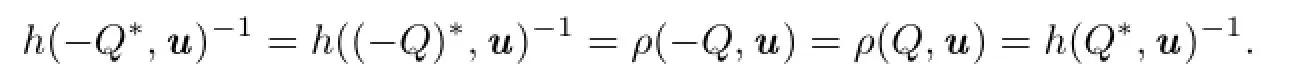
Therefore,−Q∗=Q∗.This shows that Q∗is also an origin-symmetric convex body.Namely,Taking Q∗=[−u,u]for any u∈Sn−1,then for every v∈Sn−1,h(Q∗,v)=|u·v| andholds.From this and by(1.2),we have
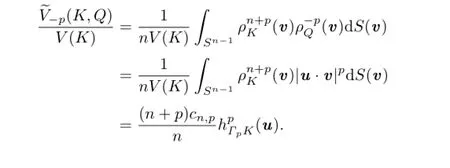
Similarly,
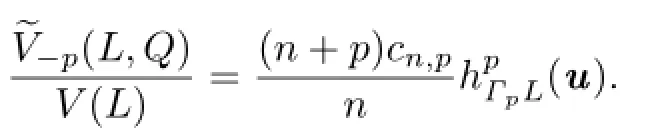
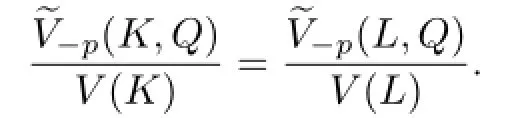

The proof of Theorem 1.2 is completed.
In order to prove Theorem 1.3,we need the following lemma.
Lemma 3.1[25]Let K,and p≥1.If either
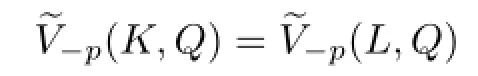
or
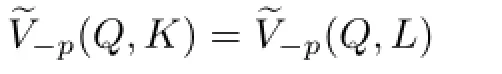
Proof of Theorem 1.3 By Theorem 1.2,we know that if K,p≥1 and p is not an even integer,then ΓpK=ΓpL if and only if
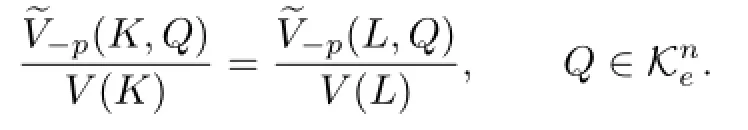
Because
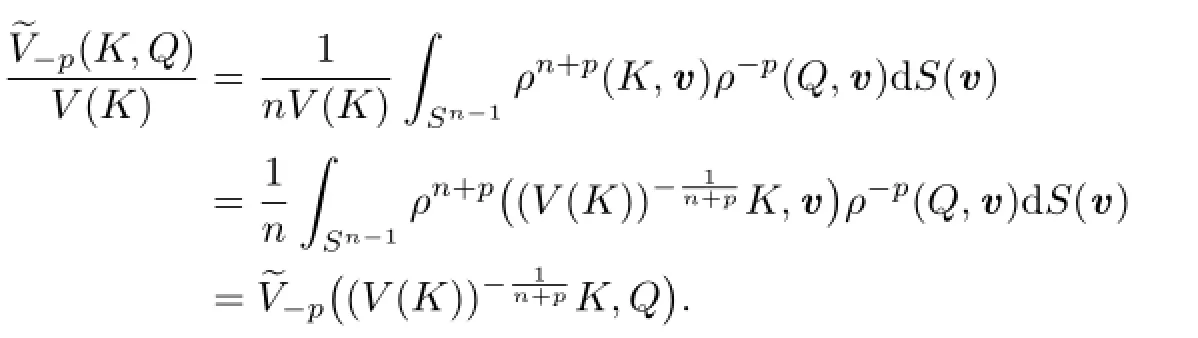
Similarly,
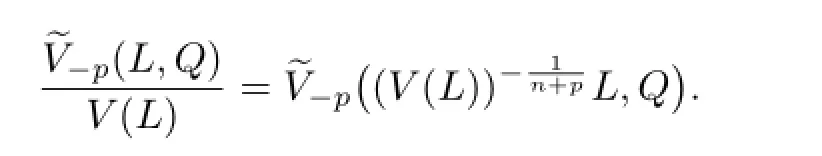
Then

According to Lemma 3.1,we know that(3.4)holds if and only if

This shows that K and L are dilates.
On the contrary,if K and L are dilates,we may assume that K=λL,where λ is an arbitrary positive real number.In particular,we make
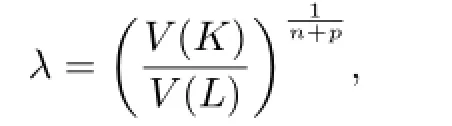
by the reversibility of the above process of argumentation,and we know that ΓpK=ΓpL.
4 Shephard Problems for Lp-centroid Bodies
In this section,we complete the proof of Theorem 1.4,and give a new proof of Theorem 1.1. Proof of Theorem 1.4 Taking Q=L in Theorem 1.2,and using Minkowski's inequality (2.6)for dual Lp-mixed volumes,we have
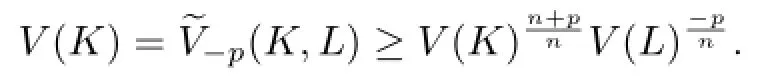
After simplify,we can get

Namely,V(K)≤V(L)with equality if and only if K and L are dilates.Let L=λK.And together with the condition ΓpK=ΓpL,it shows that

Therefore,λ=1.From this,we know that equality in the inequality of Theorem 1.4 is true if and only if K=L.
Finally,we give a new proof of Theorem 1.1.To prove Theorem 1.1,we need several lemmas.
Lemma 4.1[12,26]Let K,,p≥1 and satisfy ΓpK⊆ΓpK.Then for any

with equality if and only if ΓpK=ΓpL.
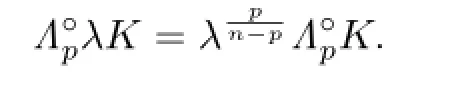
Proof. By using the definition(2.17)of Lp-pole curvature image and

we have
This shows that
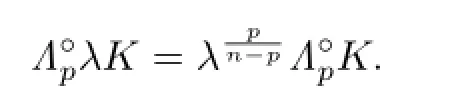
This completes the proof.
Now define a class:


with equality if and only if ΓpK=ΓpL.

Similarly,we can get
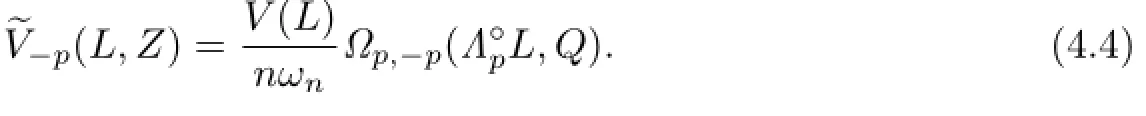
From(4.3)and(4.4),it shows that
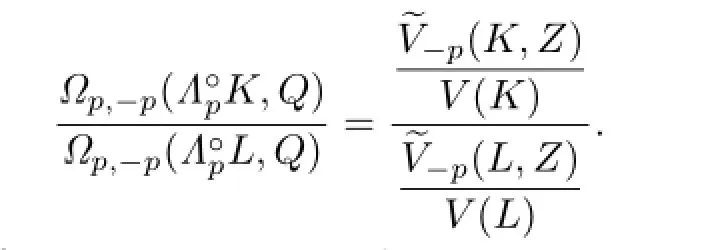
Because ΓpK⊆ΓpL,then from Lemma 4.1,we have
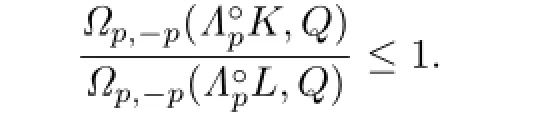
Namely,
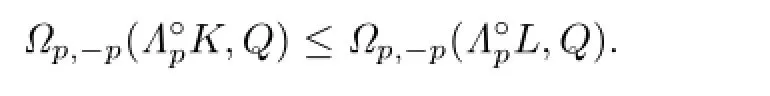
According to the conditions of equality in inequality(4.1),we know that equality holds in inequality(4.2)if and only if ΓpK=ΓpL.
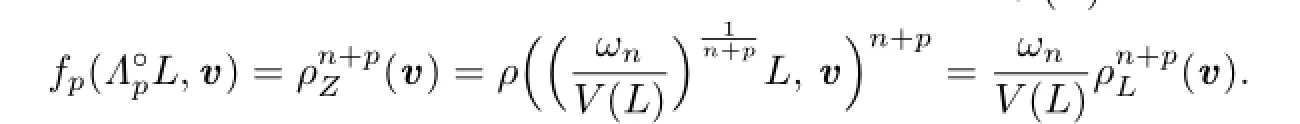
Therefore,from(4.2)and(2.16),we have
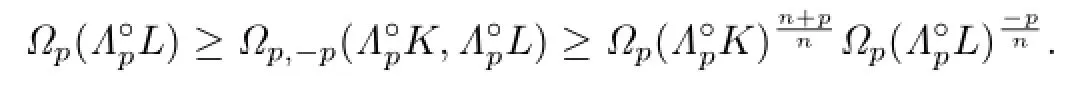
This shows that

From
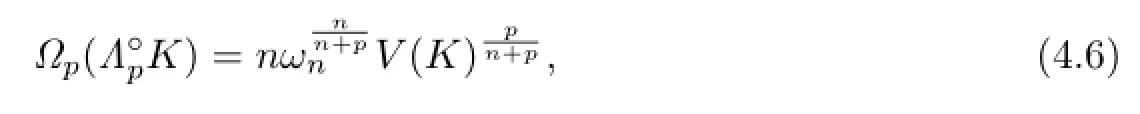
this yields

According to the conditions of equality in inequalities(2.16)and(4.2),we know that equality holds in inequality(4.7)for n̸=p>1 if and only ifandare dilates and ΓpK=ΓpL;For n̸=p=1 if and only ifandare homothetic and ΓK=ΓL.
For the case n̸=p>1 of equality that holds in(4.7),we may suppose thatand together with Lemma 4.2,we getThus,from thedefinition of Lp-pole curvature image,we have

Namely,

This shows that K and L are dilates.Without loss of generality,assume K=λL(λ>0), and by using ΓpL=ΓpK=ΓpλL=λpΓpL,we have λ=1.Therefore,we know that equality holds in inequality(4.7)for n̸=p>1 if and only if K=L.
For the case n̸=p=1 of equality that holds in(4.7),we may take0,x∈Rn).Combining with Lemma 4.2,it shows thatNoting that
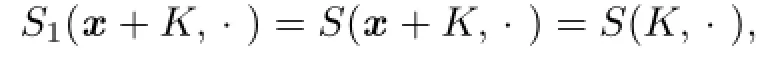
then we have

Thus,by using the definition(2.17)of Lp-pole curvature image,we have

Namely,
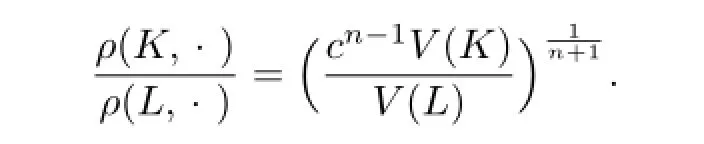
This shows that K and L are dilates.Without loss of generality,assuming K=λL(λ>0), and by using ΓL=ΓK=ΓλL=λΓL,we have λ=1.Therefore,we know that equality holds in inequality(4.7)for n̸=p=1 if and only if K=L.
[1]Schneider R.Convex Bodies:The Brunn-Minkowski Theory.Cambridge:Cambridge Univ. Press,1993.
[2]Petty C M.Centroid surface.Pacific J.Math.,1961,11:1535–1547.
[3]Lutwak E,Zhang G Y.Blaschke-Santal´o inequalities.J.Differential Geom.,1997,47:1–16.
[4]Lonke Y.Derivatives of the Lp-cosine transform.Adv.Math.,2003,176:175–186.
[5]Lutwak E.Mixed projection inequalities.Trans.Amer.Math.Soc.,1985,287:91–106.
[6]Lutwak E.On some affine isoperimetric inequalities.J.Differential Geom.,1986,56:1–13.
[7]Lutwak E.Centroid bodies and dual mixed volumes.Proc.London Math.Soc.,1990,60: 365–391.
[8]Zhang G Y.Centered bodies and dual mixed volumes.Trans.Amer.Math.Soc.,1994,345: 777–801.
[9]Zhang G Y.Intersection bodies and the Busemann-Petty inequalities in R4.Annals.Math., 1994,140:331–346.
[10]Zhang G Y.A positive solution to the Busemann-Petty problem in R4.Annals.Math.,1999, 149:535–543.
[11]Koldobsky A.Generalized Levy representation of norms and isometric embeddings into Lpspaces.Ann.Inst.H.Poincar´e Probab.Statist.,1992,28:335–353.
[12]Grinberg E,Zhang G Y.Convolutions,transforms and convex bodies.Proc.London Math. Soc.,1999,78:77–115.
[13]Gardner R J.Geometric Tomography.Gambridge:Gambridge Univ.Press,1995.
[14]Firey W J.Polar means of convex bodies and a dual to the Brunn-Minkowski theorem.Canad. J.Math.,1961,13:444–453.
[15]Firey W J.Mean cross-section measures of harmonic means of convex bodies.Pacific J.Math., 1961,11:1263–1266.
[16]Lutwak E.The Brunn-Minkowski-Firey theory II:Affine and geominimal surface areas.Adv. Math.,1996,118:244–294.
[17]Lutwak E,Yang D,Zhang G Y.Lp-affine isoperimetric inequalities.J.Differential Geom., 2000,56:111–132.
[18]Koldobaky A L.Inverse formula for the Blaschke-Levy representation.Houston J.Math.,1997, 23:95–108.
[19]Neyman A.Representation of Lp-norms and isometric embedding in Lp-spaces.Israel J.Math., 1984,48:129–138.
[20]Rubin B.Inversion of fractional integrals related to the spherical Radon transform.J.Funct. Anal.,1998,157:470–487.
[21]Rubin B.Intersection bodies and generalized cosine transforms.Adv.Math.,2008,218:696–727.
[22]Lutwak E.Extended affine surface area.Adv.Math.,1991,85:39–68.
[23]Yuan J,Lv S J,Leng G S.The p-affine surface area.Math.Inequal.Appl.,2007,10(3):693–702.
[24]Zu X Y,Lv S J,Leng G S.Extended affine surface area and zonotopes.Bol.Soc.Mat., Mexicanc,2008,14:125–138.
[25]Ma T Y.On Lp-mixed centroid bodies and dual Lp-mixed centroid bodies(in Chinese).Acta Math.Sinica,2010,53(2):301–314.
[26]Yuan J,Zhao L Z,Leng G S.Inequalities for Lp-centroid body.Taiwanese J.Math.,2008, 29(2):209–220.
A
1674-5647(2015)04-0333-12
10.13447/j.1674-5647.2015.04.05
Received date:Feb.21,2014.
The NSF(11161019,11371224)of China and the STP(145RJZG227)of Gansu.
E-mail address:matongyi@126.com(Ma T Y).
2010 MR subject classification:52A40,52A20
 Communications in Mathematical Research2015年4期
Communications in Mathematical Research2015年4期
- Communications in Mathematical Research的其它文章
- The Representive of Metric Projection on the Finite Codimension Subspacein Banach Space
- On Weakly P.P.Rings
- Stability of Semi-implicit Finite Volume Scheme for Level Set Like Equation
- Self-dual Codes with Symplectic Inner Product
- Biquartic Finite Volume Element Method Based on Lobatto-Guass Structure
- Co-commuting Mappings of Generalized Matrix Algebras
