Dynamics of a Delayed Predator-prey System with Stage Structure for Predator and Prey
LIU JUANAND ZHANG ZI-ZHEN
(1.Department of Mathematics and Physics,Bengbu College,Bengbu,Anhui,233030)
(2.School of Management Science and Engineering,Anhui University of Finance and Economics,Bengbu,Anhui,233030)
Communicated by Li Yong
Dynamics of a Delayed Predator-prey System with Stage Structure for Predator and Prey
LIU JUAN1AND ZHANG ZI-ZHEN2
(1.Department of Mathematics and Physics,Bengbu College,Bengbu,Anhui,233030)
(2.School of Management Science and Engineering,Anhui University of Finance and Economics,Bengbu,Anhui,233030)
Communicated by Li Yong
In this paper,a predator-prey system with two discrete delays and stage structure for both the predator and the prey is investigated.The dynamical behaviors such as local stability and local Hopf bifurcation are analyzed by regarding the possible combinations of the two delays as bifurcating parameter.Some explicit formulae determining the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions are derived by using the normal form method and the center manifold theory.Finally,numerical simulations are presented to support the theoretical analysis.
time delay,stage-structure,Hopf bifurcation,stability,periodic solution
1 Introduction
Predator-prey systems have been studied by many authors due to their universal existence and importance(see[1–5]).It is well known that there are many species whose individual members have a life history that takes them through immature stage and mature stage. Based on this fact,stage-structured predator-prey systems have been investigated by many authors in recent years(see[6–13]).A stage-structured system of one species'growth consisting of immature and mature individuals was investigated by Aiello and Freedman[3].Li F and Li H W[5]investigated a predator-prey system with stage structure for the prey:
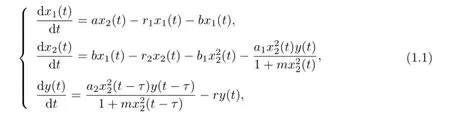
where x1(t)and x2(t)represent the densities of the immature prey and the mature prey at time t,respectively.y(t)represents the density of the predator at time t.They studied the Hopf bifurcation phenomenon and properties of periodic solutions of(1.1).Xu[6]considered the following predator-prey system with stage structure for the predator:
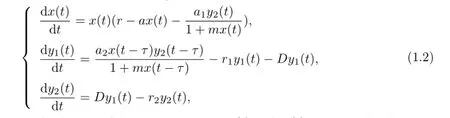
where x(t)represents the density of the prey at time t.y1(t)and y2(t)represent the densities of the immature predator and the mature predator at time t,respectively.He investigated the permanence and local and global stability of(1.2).
Motivated by the work above,and considering that both predator and prey have a life history that takes them through immature stage and mature stage,we propose the following delayed system with Holling-III functional response in the present paper:
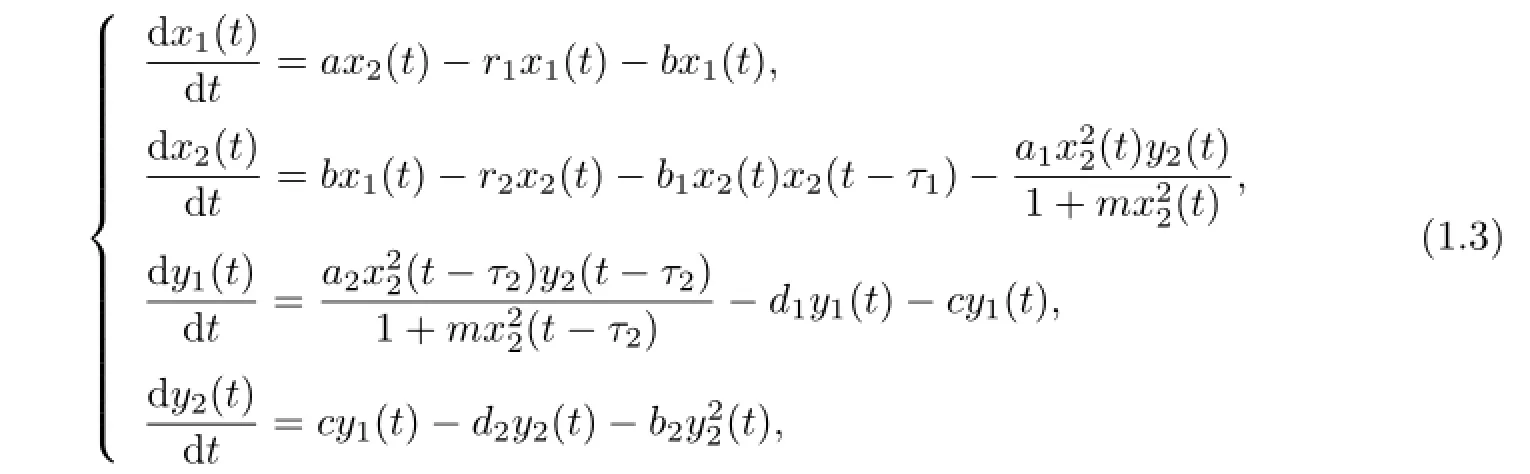
The rest of this paper is organized as follows.In Section 2,local stability of the positive equilibrium and the existence of Hopf bifurcation are discussed.The direction of Hopf bifurcation and the stability of periodic solutions are determined in Section 3.To verify the theoretical analysis in this paper,some numerical simulations are also presented in Section 4.
2 Stability and Existence of Local Hopf Bifurcation
In this section,we study the local stability of the positive equilibrium of(1.3)and the existence of the local Hopf bifurcation at the positive equilibrium of(1.3).It is not difficult to verify that if the conditions
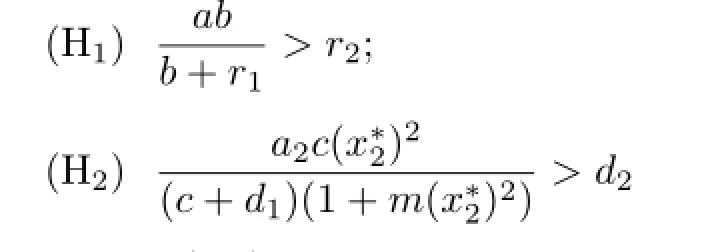
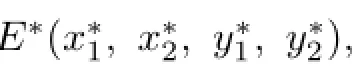

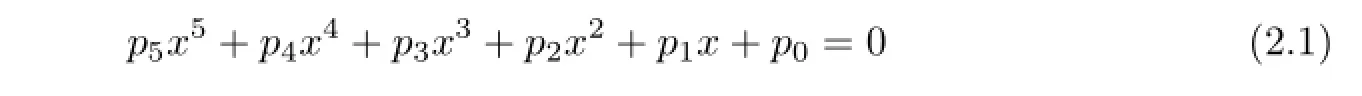
with
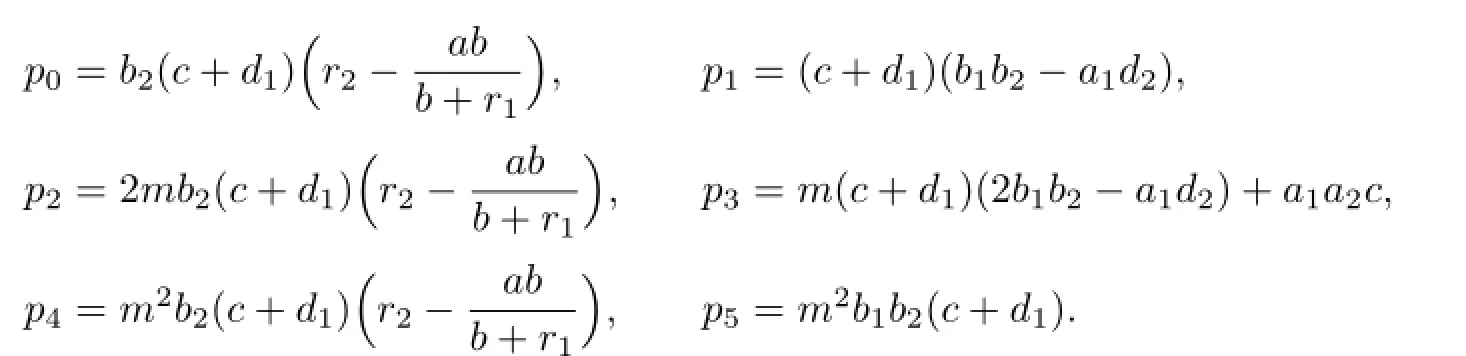
Let
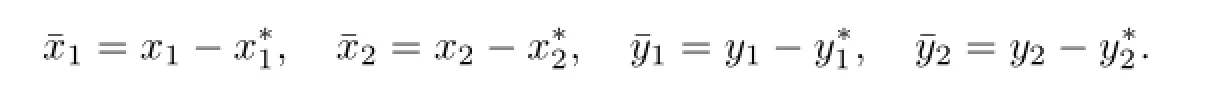
Dropping the bars,(1.3)can be transformed into the following form:
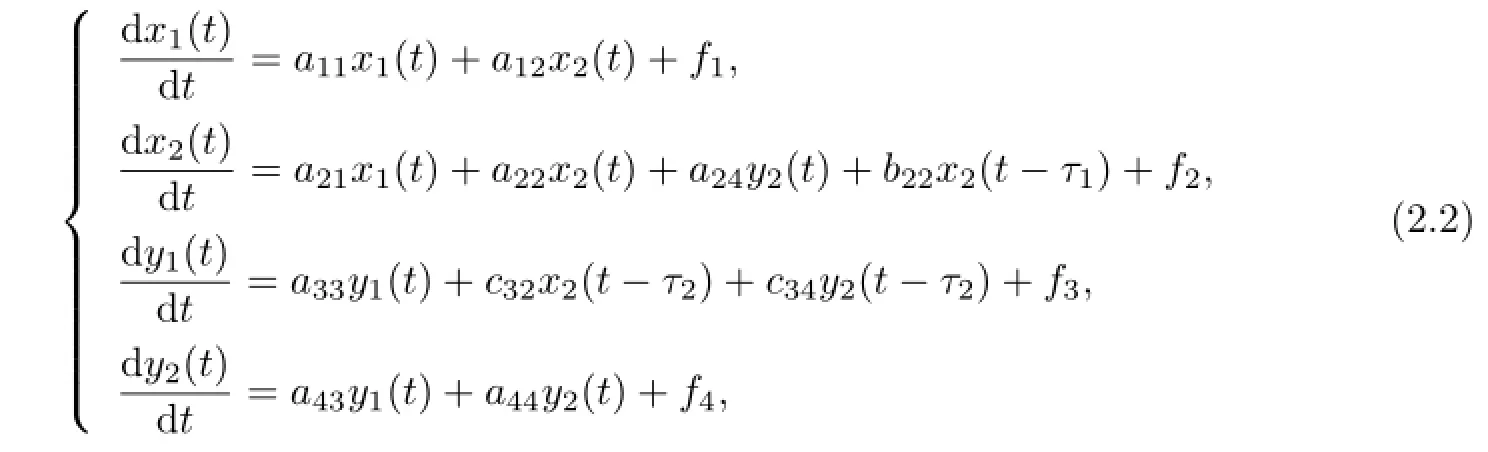
where
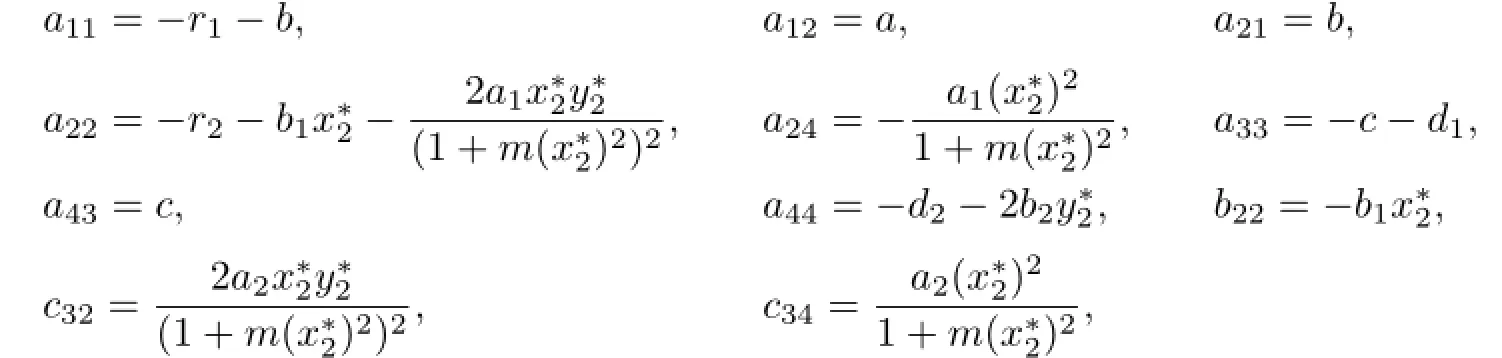
and
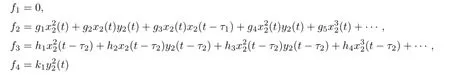
with
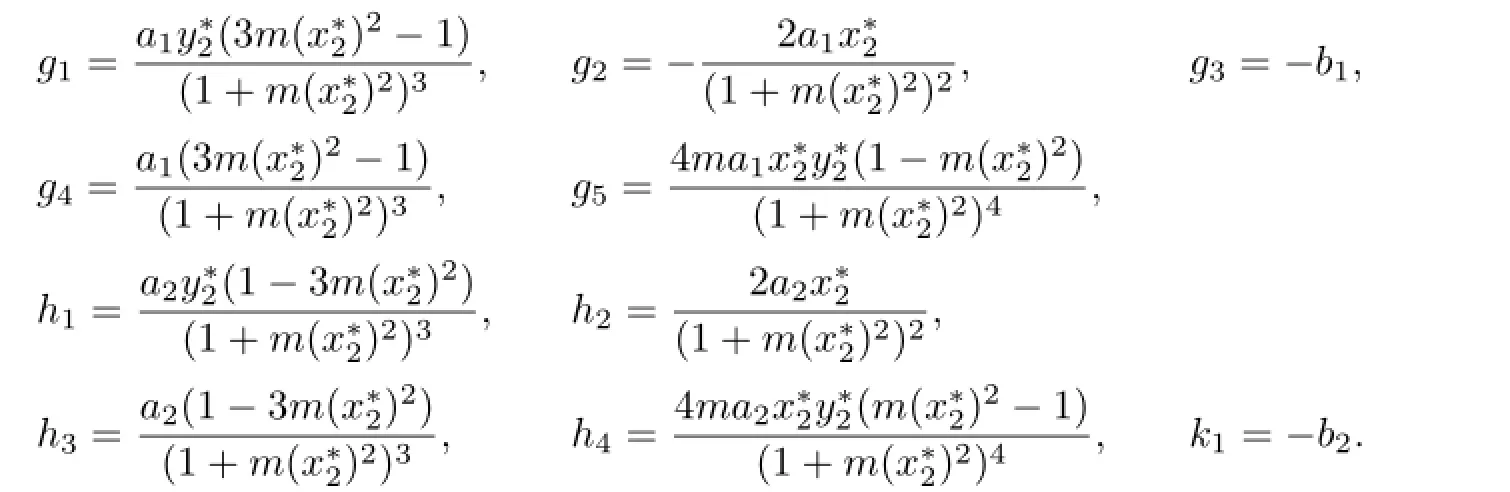
The linear system of(2.2)is
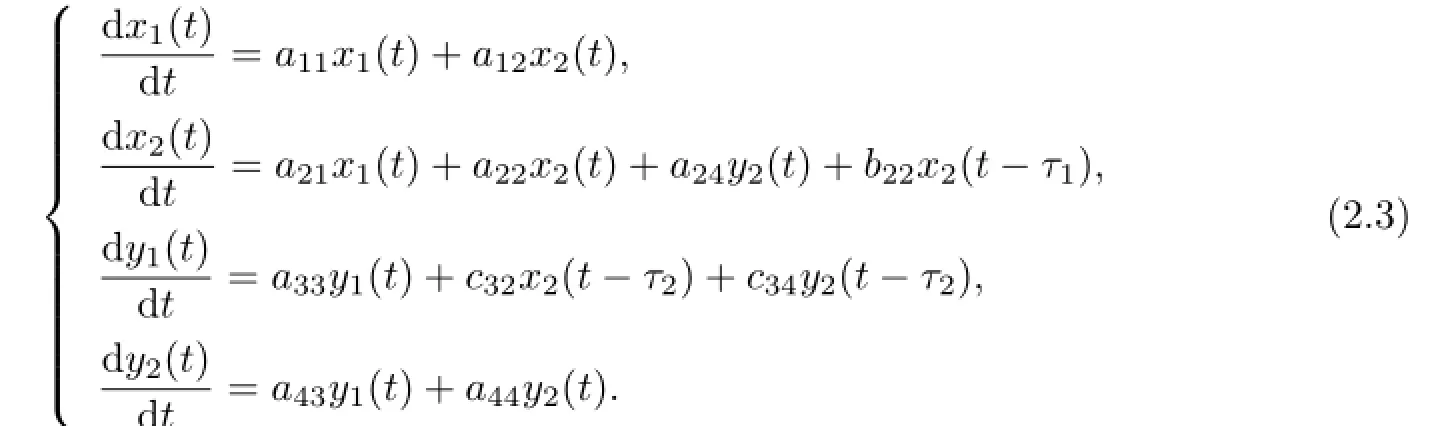
The characteristic equation of(2.3)is as follows:
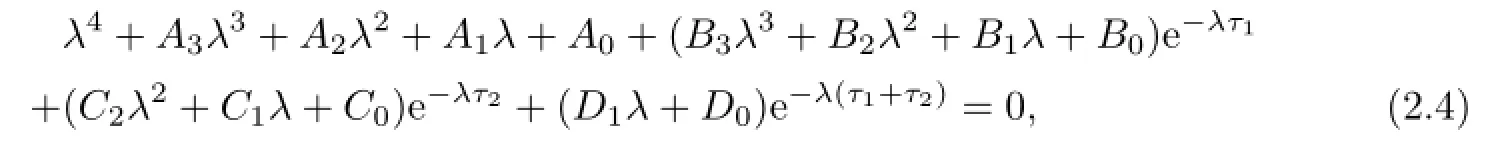
where
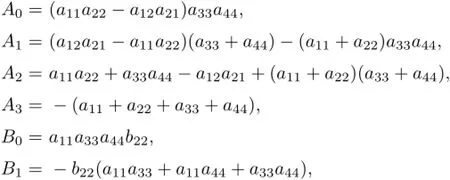
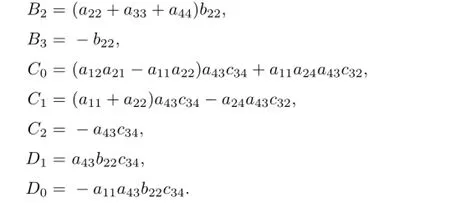
Case 1.τ1=τ2=0.
For τ1=τ2=0,(2.4)can be rewritten as

where
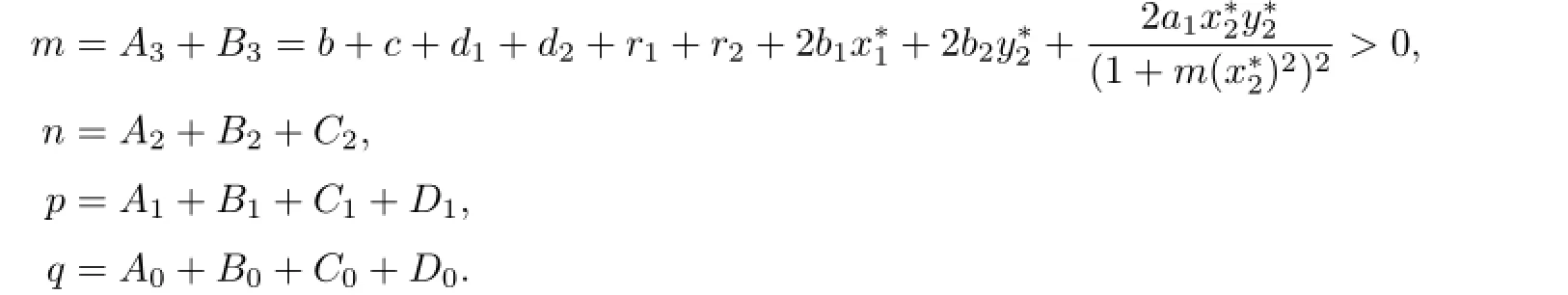
Therefore,by the Routh-Hurwithz theorem,if the following conditions hold:
(H11)q>0,mn>p;
(H12)mnp>p2+m2q,
then the positive equilibriumof(1.3)without time delay is locally asymptotically stable.
Case 2.τ1>0,τ2=0.
When τ2=0,(2.4)becomes
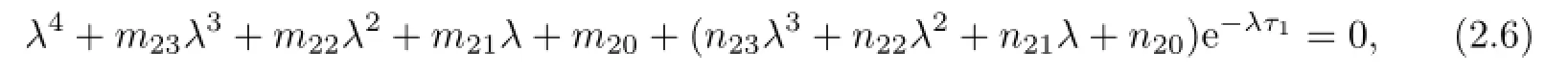
where
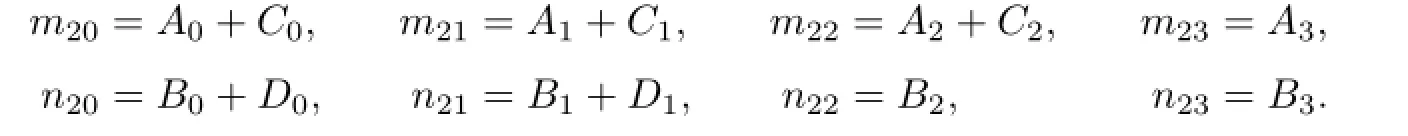
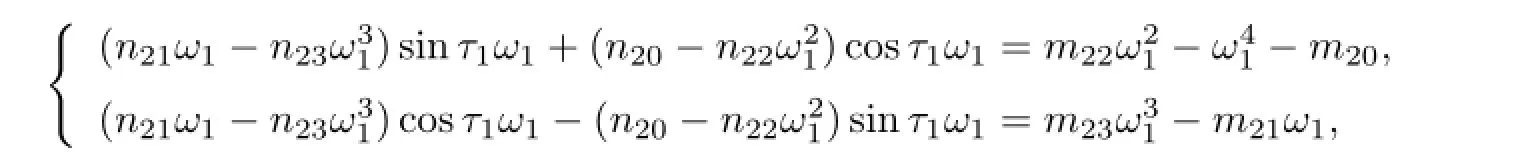
which follows that
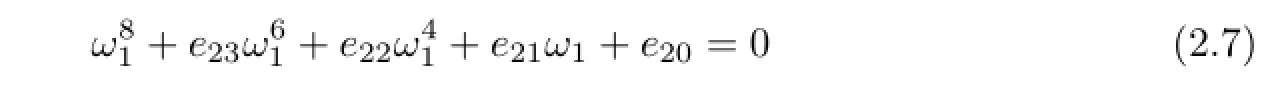
with
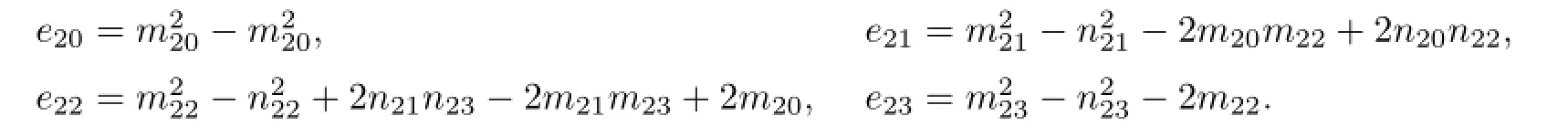
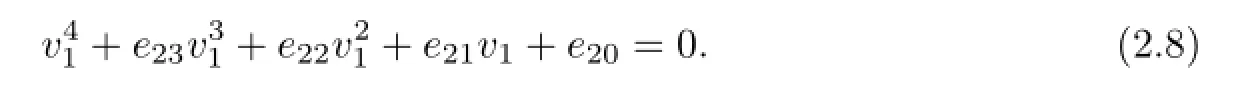
According to Lemma 2.1 in[14],we give the following assumption.
(H21)(2.8)has at least one positive real root.
Without loss of generality,we assume that(2.8)has four positiveroots which are denoted as v11,v12,v13and v14.Then(2.7)has four positive rootsk=1,2,3,4.And for every fixed ω1k,k=1,2,3,4,the corresponding critical value of time delayis
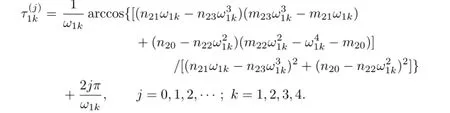
Let
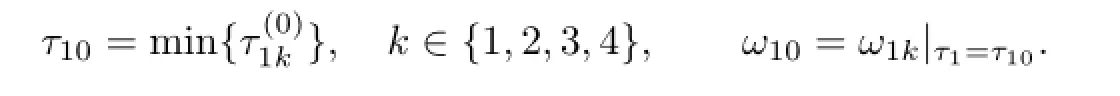
Differentiating both sides of(2.6)regarding τ1,and substituting λ=iω10into it,we get
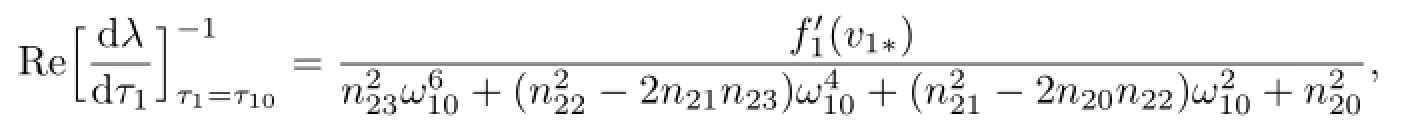
where
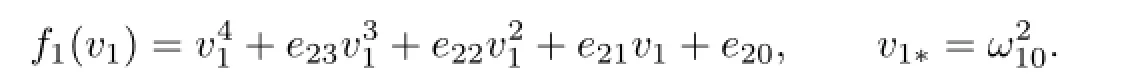
Therefore,if the condition
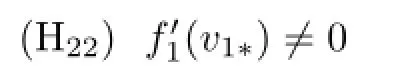
holds,then
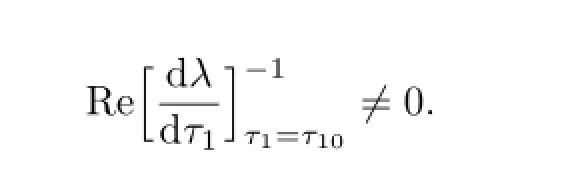
Namely,if the condition(H22)holds,then the transversality condition is satisfied.By the Hopf bifurcation theorem,we have the following results.
Theorem 2.1 If the conditions(H21)and(H22)hold,then
(i) the positive equilibriumof(1.3)is asymptotically stable for τ1∈[0,τ10);
(ii)(1.3)undergoes a Hopf bifurcation at the equilibriumand a family of periodic solutions bifurcate fromnear τ1=τ10.
Case 3.τ1=0,τ2>0.
When τ1=0,(2.4)becomes
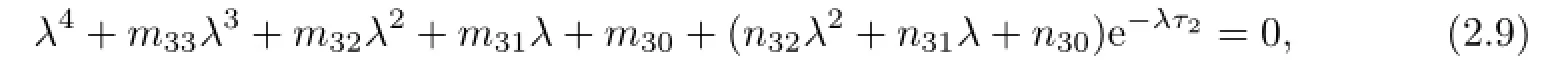
where
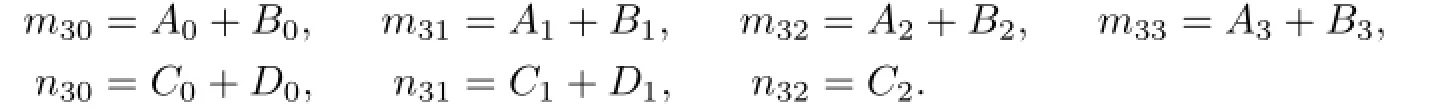
It follows that
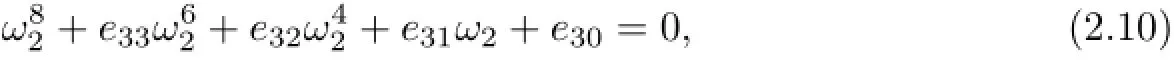
where
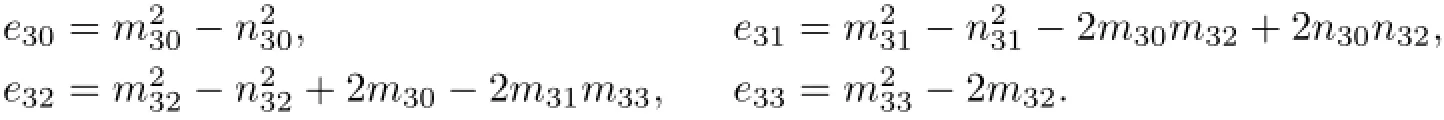
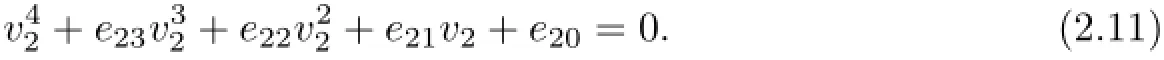
Define
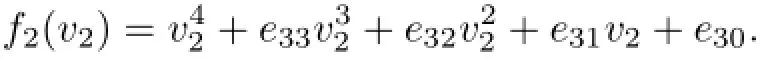
Similar as in Case 2,we make the following assumption.
(H31)(2.11)has least at one positive real root.
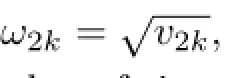
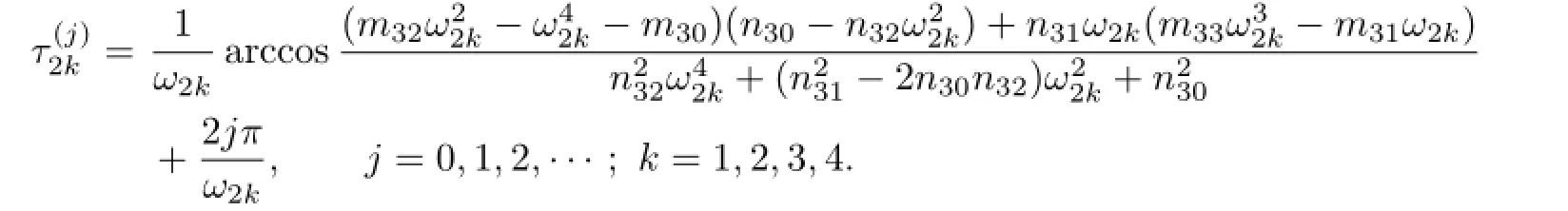
Let
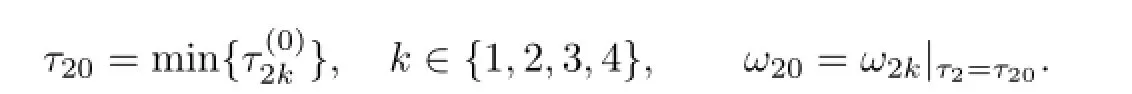
Similar as in Case 2,we can conclude that if the condition
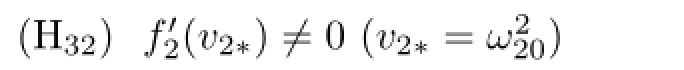
holds,then the transversality condition is satisfied.Therefore,we have the following results.
Theorem 2.2 If the conditions(H31)and(H32)hold,then
(i) the positive equilibriumof(1.3)is asymptotically stable for τ2∈[0,τ20);
(ii)(1.3)undergoes a Hopf bifurcation at the equilibrium,and a family of periodic solutions bifurcate fromnear τ2=τ20.
Case 4.τ1>0,τ2>0 and τ2∈(0,τ20).
We consider(1.3)with τ2in its stable interval and τ1is considered as a parameter.Let λ=iω1∗(ω1∗>0)be the root of(2.4).Then we can get
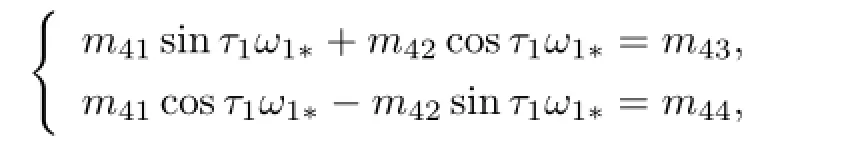
where
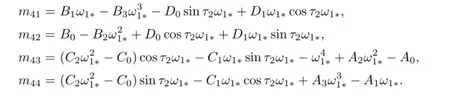
It follows that
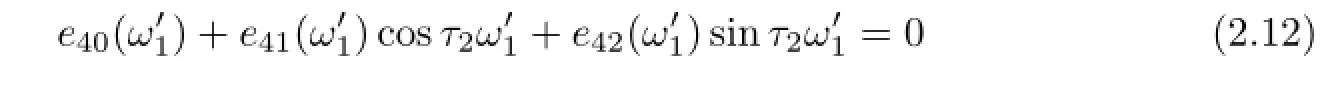
with
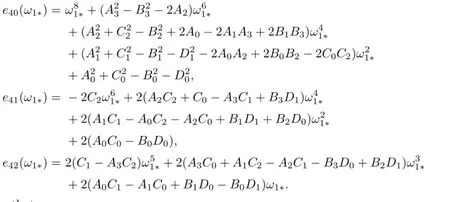
Suppose that
(H41)(2.12)has at least finite positive real roots.
We denote the positive roots of(2.12)as ω11∗,ω12∗,···,ω1k∗.Then,for every fixed ω1i∗(i=1,2,3,···,k),the corresponding critical value of time delay{τ(j)1i∗|j=0,1,2,···}is
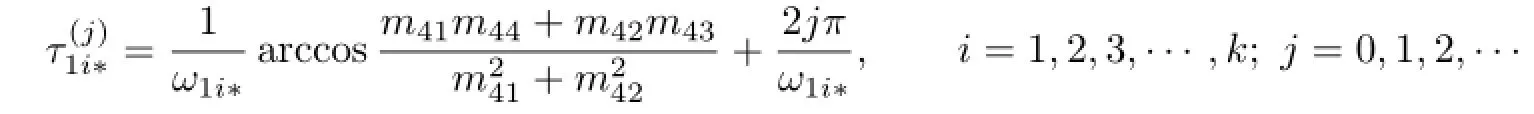
Let
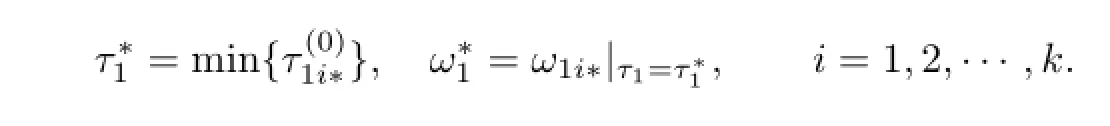
Differentiating(2.4)regarding τ1,we obtain
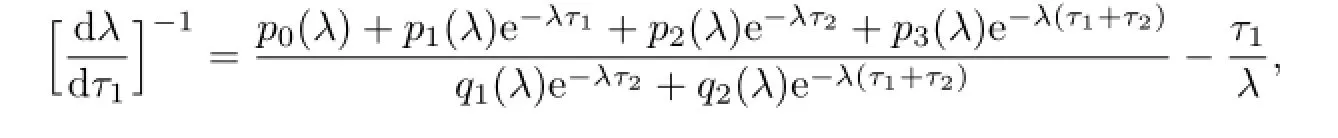
where
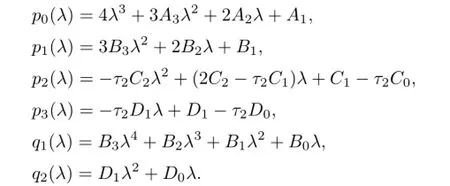
Hence,
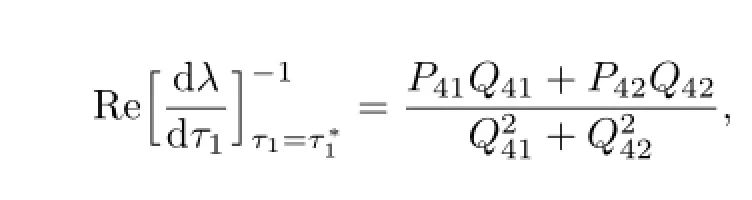
where
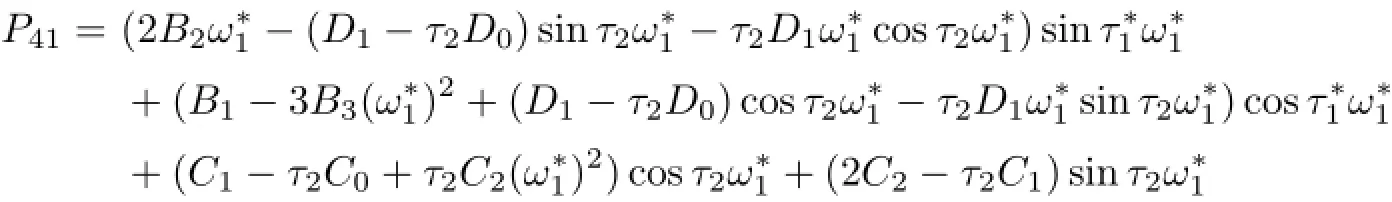
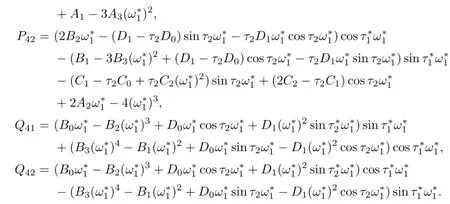
Clearly,if the condition
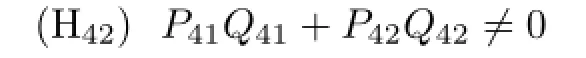
holds,then
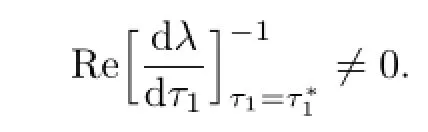
Thus,we have the following results.
Theorem 2.3 If the conditions(H41)and(H42)hold and τ2∈(0,τ20),then
(i) the positive equilibriumof(1.3)is asymptotically stable for τ1∈
(ii)(1.3)undergoes a Hopf bifurcation at the equilibriumand a family of periodic solutions bifurcate fromnear
3 Stability of the Bifurcating Periodic Solutions
In the previous section,we have obtained the sufficient conditions for Hopf bifurcation to occur for different combinations of τ1and τ2.In this section,we investigate the direction of the Hopf bifurcation and stability of the bifurcating periodic solutions of(1.3)with respect to τ1for τ2∈(0,τ20).We can get the following coefficients by using the normal form method and center manifold theory:
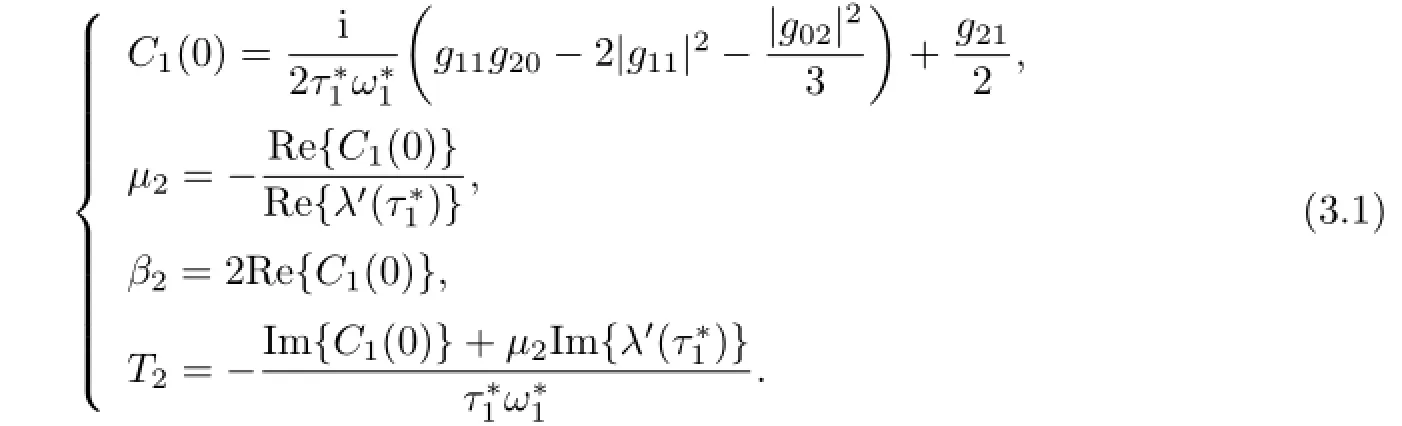
In conclusion we can get the following theorem.
Theorem 3.1 For(1.3),ifµ2>0(µ2<0),the Hopf bifurcation is supercritical(subcritical);if β2<0(β2>0),the bifurcating periodic solutions are stable(unstable);if T2>0 (T2<0),the period of the bifurcating periodic solutions increases(decreases).
4 Numerical Simulation
In order to verify the theoretical analysis in Sections 2 and 3,we present some numerical simulations in this section.We consider the following system:
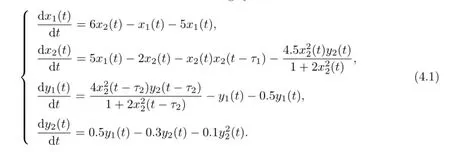
It is not difficult to get that(4.1)has a unique positive equilibrium E∗(0.9661,0.9661, 1.1643,1.3410)by the software package Matlab.Then,we can get m=13.4192,n=24.2229, p=7.5628,q=5.9669 and mn>p,mnp>p2+m2q.That is,the conditions(H11)and (H12)hold.
For τ1>0,τ2=0,by a complex computation,we have ω10=0.6517,τ10=1.1162. Then we get fTherefore,the conditions(H21)and(H22)hold.Thus, by Theorem 2.1,we know that the positive equilibrium E∗is asymptotically stable for τ1∈[0,1.1162)and E∗becomes unstable once τ1>τ10=1.1162,which can be illustrated by Figs.4.1 and 4.2.As can be seen from Fig.4.1 that when τ1=1.05∈[0,1.1162),the positive equilibrium E∗is asymptotically stable.However,when τ1=1.25>τ10=1.1162, the positive equilibrium E∗becomes unstable and a Hopf bifurcation occurs at the positive equilibrium E∗.This property can be shown in Fig.4.2.Similarly,we have ω20=0.3797, τ20=1.7825 for τ1=0,τ2>0.The corresponding waveforms are shown in Figs.4.3 and 4.4.
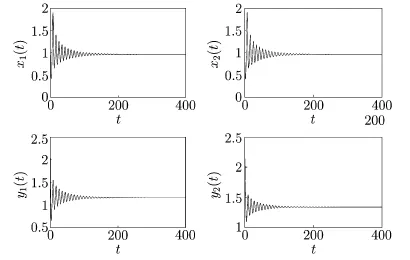
Fig.4.1 E∗is locally asymptotically stable for τ1=1.05<1.1162=τ10with initial values 1.7,1.5,2.2,2.15
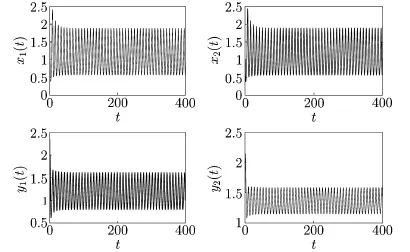
Fig.4.2 E∗is unstable for τ1=1.25>1.1162=τ10with initial values 1.7,1.5,2.2,2.15
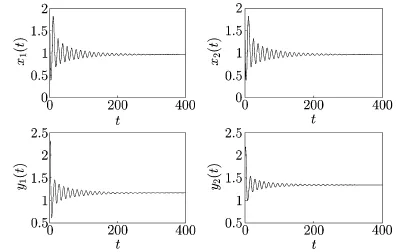
Fig.4.3 E∗is locally asymptotically stable for τ2=1.35<1.7825=τ20with initial values 1.7,1.5,2.2,2.15
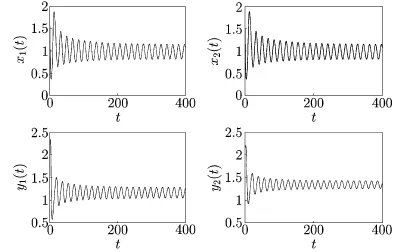
Fig.4.4 E∗is unstable for τ2=1.95>1.7825=τ20with initial values 1.7, 1.5,2.2,2.15
For τ1>0,τ2>0 and τ2=1.05∈(0,τ20),we obtainFrom Theorem 2.3,we know that the positive equilibrium E∗is asymptotically stable for τ1∈[0,0.6388)and unstable whenwhich are illustrated in Figures 4.5 and 4.6.In addition,from(3.1)we have C1(0)=−2.7701+10.6183i,µ2=9.1664>0, β2=−5.5402<0,T2=4.2985>0.Therefore,from Theorem 3.1,we can know that the Hopf bifurcation is supercritical and the bifurcating periodic solutions are stable and the period of the bifurcating periodic solutions increases.
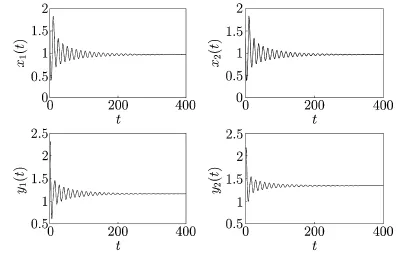
Fig.4.5 E∗is locally asymptotically stable forandwith initial values 1.7,1.5,2.2,2.15
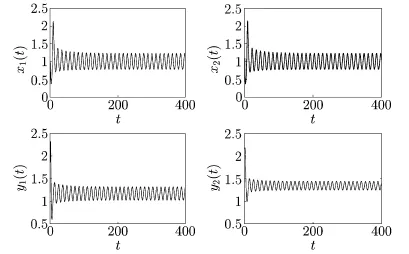
Fig.4.6 E∗is unstable forand τ2=1.05∈(0,τ20) with initial values 1.7,1.5,2.2,2.15
5 Conclusions
In the present paper,a delayed predator-prey system with stage structure is studied.Compared with the predator-prey system considered in[5]and[6],the predator-prey system in this paper classifies individuals of both predator and prey as belonging to either the immature or the mature.We incorporate two discrete delays into the system and investigate theeffects of two delays on the dynamics of the system.By taking the possible combinations of the two discrete delays in the predator-prey system as the bifurcation parameter,the local stability and existence of Hopf bifurcation are established.It has been shown that the two delays may destabilize the positive equilibrium of the system and cause the species in the system to fluctuate under certain conditions.Further,the properties of Hopf bifurcation such as direction of the Hopf bifurcation and stability of the bifurcating periodic solutions are determined by using the normal form method and center manifold theorem.Some numerical simulations are also included and from the simulations we can conclude that the species in the system can coexist in an oscillatory mode under some conditions.
[1]Yan X P,Zhang C H.Hopf bifurcation in a delayed Lokta-Volterra predator-prey system. Nonlinear Anal.Real World Appl.,2008,9(1):114–227.
[2]Xu C J,Tang X H,Liao M X,He X F.Bifurcation analysis in a delayed Lokta-Volterra predator-prey model with two delays.Nonlinear Dynam.,2011,66(1/2):169–183.
[3]Aiello W G,Freedman H I.A time delay model of single-species growth with stage structure. Math.Biosci.,1990,101(2):139–153.
[4]Wang W,Chen L.A predator-prey system with stage-structure for predator.Comput.Math. Appl.,1997,33(8):83–91.
[5]Li F,Li H W.Hopf bifurcation of a predator-prey model with time delay and stage structure for the prey.Math.Comput.Model,2012,55(3/4):672–679.
[6]Xu R.Global stability and Hopf bifurcation of a predator-prey model with stage structure and delayed predator response.Nonlinear Dynam.,2012,67(2):1683–1693.
[7]Xu R.Global dynamics of a predator-prey model with time delay and stage structure for the prey.Nonlinear Anal.Real World Appl.,2011,12(4):2151–2162.
[8]Chen F D,Xie X D,Li Z.Partial survival and extinction of a delayed predator-prey model with stage structure.Appl.Math.Comput.,2012,219(8):4157–4162.
[9]Cai L M,Yu J Y,Zhu G T.A stage-structured predator-prey model with Beddington-DeAngelis functional response.J.Appl.Math.Comput.,2008,26(1/2):85–103.
[10]Cui J A,Song X Y.Permanence of predator-prey system with stage structure.Discrete.Cont. Dyn.Syst.Ser.B,2004,4(3):547–554.
[11]Sun X K,Huo H F,Xiang H.Bifurcation and stability analysis in predator-prey model with a stage-structure for predator.Nonlinear Dynam.,2009,58(3):497–513.
[12]Liu S Q,Beretta E.A stage-structured predator-prey model of Beddington-DeAngelis type. SIAM J.Appl.Math.,2006,66(4):1101–1129.
[13]Liu S Q,Zhang J H.Coexistence and stability of predator-prey model with DeAngelis functional response and stage structure.J.Math.Anal.Appl.,342(1):446–460.
[14]Zhang T,Liu J,Teng Z.Stability of Hopf bifurcation of a delayed SIRS epidemic model with stage structure.Nonlinear Anal.Real World Appl.,2010,11(1):293–306.
A
1674-5647(2015)04-0298-13
10.13447/j.1674-5647.2015.04.02
Received date:Jan.16,2014.
The NSF(KJ2013A003,KJ2013B137)of the Higher Education Institutions of Anhui Province.
E-mail address:my7216@163.com(Liu J).
2000 MR subject classification:34C05,34D30
 Communications in Mathematical Research2015年4期
Communications in Mathematical Research2015年4期
- Communications in Mathematical Research的其它文章
- The Representive of Metric Projection on the Finite Codimension Subspacein Banach Space
- On Weakly P.P.Rings
- Stability of Semi-implicit Finite Volume Scheme for Level Set Like Equation
- Self-dual Codes with Symplectic Inner Product
- Lp-centroid Bodies and Its Characterizations
- Biquartic Finite Volume Element Method Based on Lobatto-Guass Structure
