Boundedness of Commutators Generated by Campanato-type Functions and Riesz Transforms Associated with Schr¨odinger Operators

MO HUI-XIA,YU DONG-yAN AND SUI XIN

(School of Science,Beijing University of Posts and Telecommunications,Beijing,100876)

Communicated by Ji You-qing

Boundedness of Commutators Generated by Campanato-type Functions and Riesz Transforms Associated with Schr¨odinger Operators

MO HUI-XIA,YU DONG-yAN AND SUI XIN

(School of Science,Beijing University of Posts and Telecommunications,Beijing,100876)

Communicated by Ji You-qing

Let L=−Δ+V be a Schr¨odinger operator on Rn,n＞3,where Δ is the Laplacian on Rnand V̸=0 is a nonnegative function satisfying the reverse H¨older's inequality.Let[b,T]be the commutator generated by the Campanatotype functionand the Riesz transform associated with Schr¨odinger operatorIn the paper,we establish the boundedness of[b,T]on Lebesgue spaces and Campanato-type spaces.

commutator,Campanato-type space,Riesz transform,Schr¨odinger operator

1 Introduction

Let L=−Δ+V be a Schr¨odinger operator on Rn,n＞3,where Δ is the Laplacian on Rnand V̸=0 is a nonnegative locally integrable function.The problems related to the Schr¨odinger operators L have attracted much attention(see[1–3]for example).In particular, Fefferman[1],Shen[2]and Zhong[3]established some basic results about the fundamental solutions and the boundedness of Riesz transforms associated with the Schr¨odinger operator.

The commutators generated by the Riesz transform associated with Schr¨odinger operator and BMO functions or Lipschitz functions also attract much attention(see[4–7]for example).Chu[8]considered the boudedness of commutators generalized by the BMOLfunctionand the Riesz transformon Lebesgue spaces.And Jiang[9]investigates some

properties of the Riesz potentialon the Campanato-type spacesInspired by[4,6,8–9],in this paper we consider the boundedness of commutators generated by the Campanato-type functionand the Riesz transformon Lebesgue spaces and Campanato-type spaces.

Firstly,let us introduce some notations.A nonnegative locally Lq(Rn)integrable function V is said to belong to Bq(1＜q＜∞)if there exists a constant C=C(q,V)＞0 such that the reverse H¨older's inequality

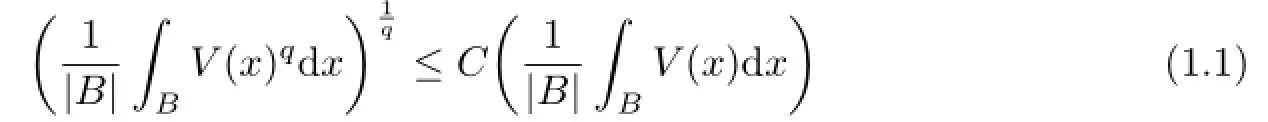
holds for any ball B in Rn.

We also say a nonnegative function V∈B∞,if there exists a constant C＞0 such that

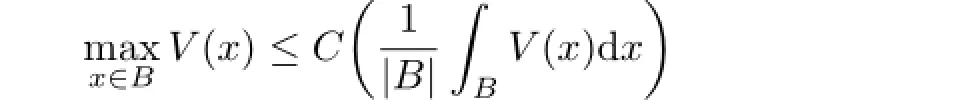
holds for any ball B in Rn.

By H¨older's inequality,we have Bq1⊂Bq2for q1＞q2＞1.One remarkable feature about the Bqclass is that if V ∈Bqfor some q＞1,then there exists an ε＞0 which depends only on n and the constant C in(1.1)such that V∈Bq+ε.It is also well known that if V∈Bq(q＞1),then V(x)dx is a doubling measure,namely,for any r＞0,x∈Rnand some constant C0,we have

∫

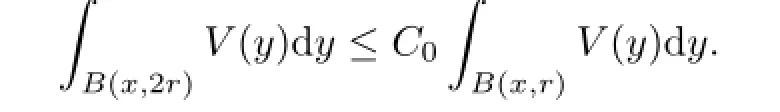
Definition 1.1[3]For x∈Rn,the function m(x,V)is defined by

Clearly,0＜m(x,V)＜1 for every x∈Rnand if r=m(x,V),then

Definition 1.3[8]Let f∈Lloc(Rn).Then the sharp maximal function associated with L=−Δ+V is defined by

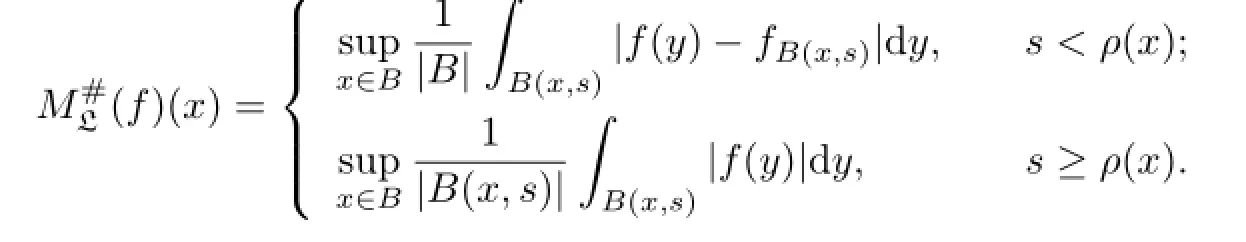
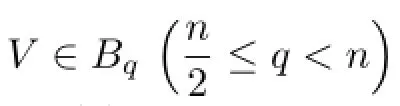
Then the kernel K(x,y)of operatorsatisfies the following estimates:there exists a constant δ＞0 such that for any nonnegative integer i,

Hence,for 1＜p≤p0,there exists a constant C＞0 such that

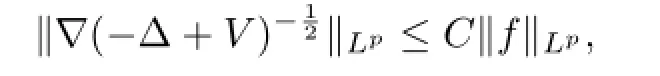
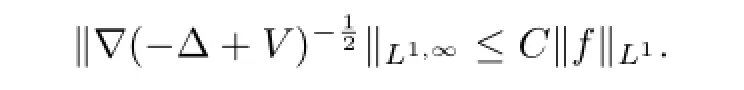
Throughout this paper,C always remains to denote a positive constant that may vary at each occurrence but is independent of the essential variable.

2 Theorems and Lemmas

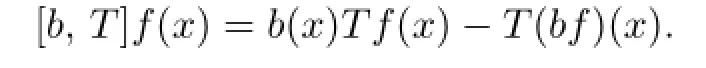
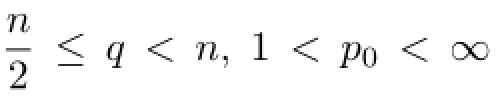
C＞0 and 1＜r＜p0such that

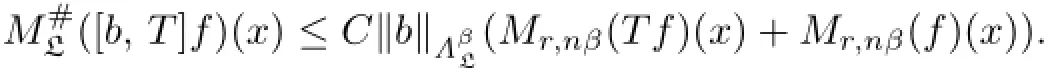
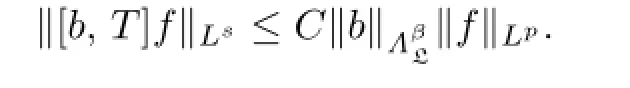
To prove the theorems,we need the following lemmas.

Lemma 2.1[8]Let 0＜p0＜∞,p0≤p＜∞ and δ＞0.If f satisfies the conditionthen there exists a constant C＞0 such that

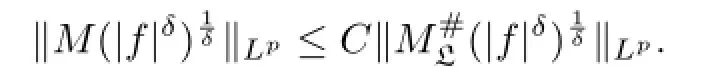
Lemma 2.2[12]For 1≤γ＜∞and β＞0,let

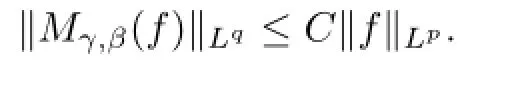
Lemma 2.3 Let B=B(x,r)and 0＜r＜ρ(x).ThenHence

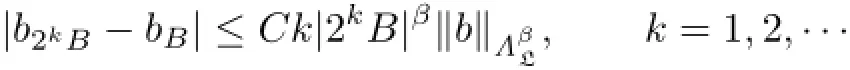
Proof.

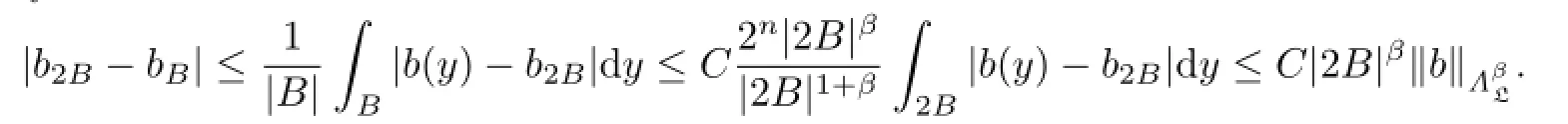
Thus,

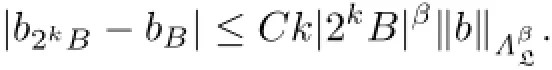
3 Proofs of Theorems 2.1–2.3

Proof of Theorem 2.1

Fix a ball B=B(x,r0).Let B∗=2B=B(x,2r0)and denote f0=fχB∗,f∞=f−f0for f∈Lloc(Rn).

Case I.When 0＜r0＜ρ(x),write

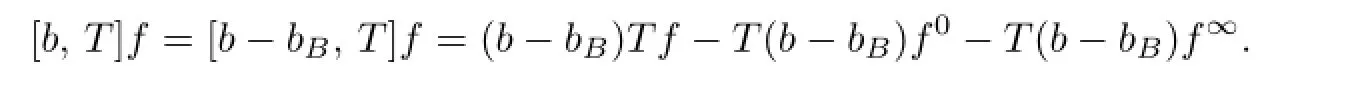
Taking

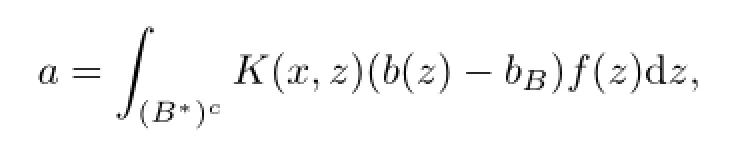
we get

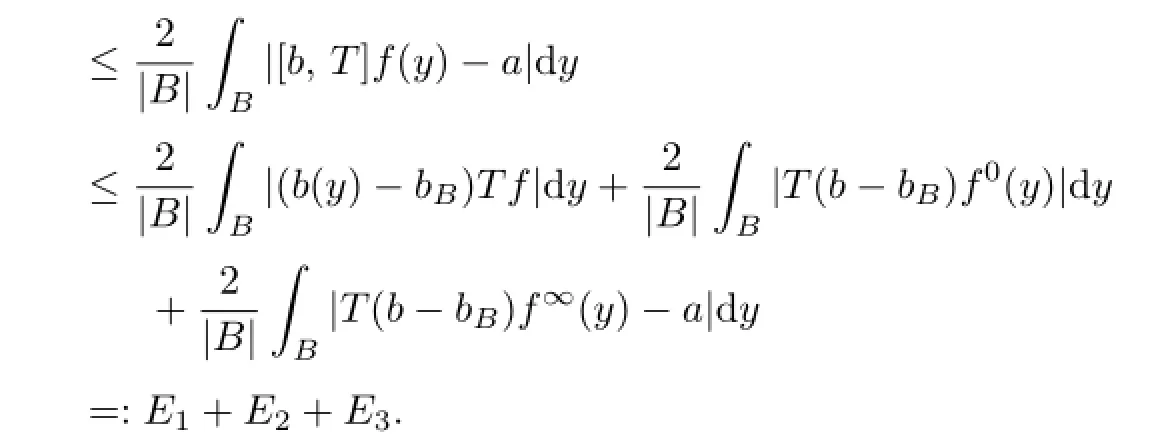
Let us estimate every part.For E1,by H¨older's inequality,we obtain

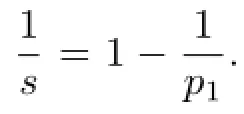
For E3,recalling δ＞0,by(1.4),we get

For E31,by H¨older's inequality,we have

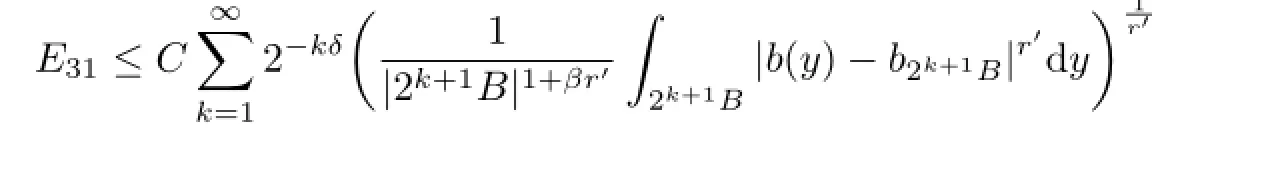
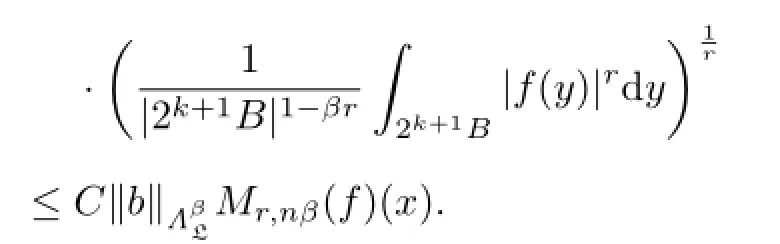
From Lemma 2.3,it follows that

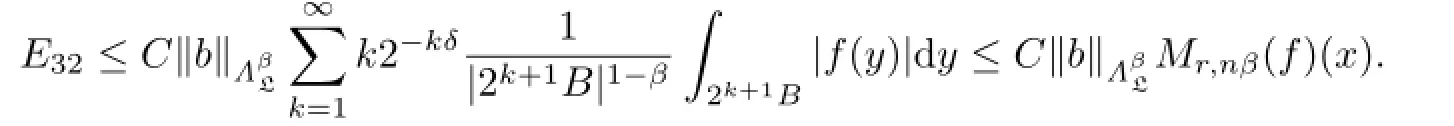
Case II.When r0≥ρ(x),write[b,T]f=bT(f)−T(bf0)−T(bf∞).Then,

For F1,by H¨older's inequality

Taking p1,p′and r as in the estimate for E2,by H¨older's inequality,we have

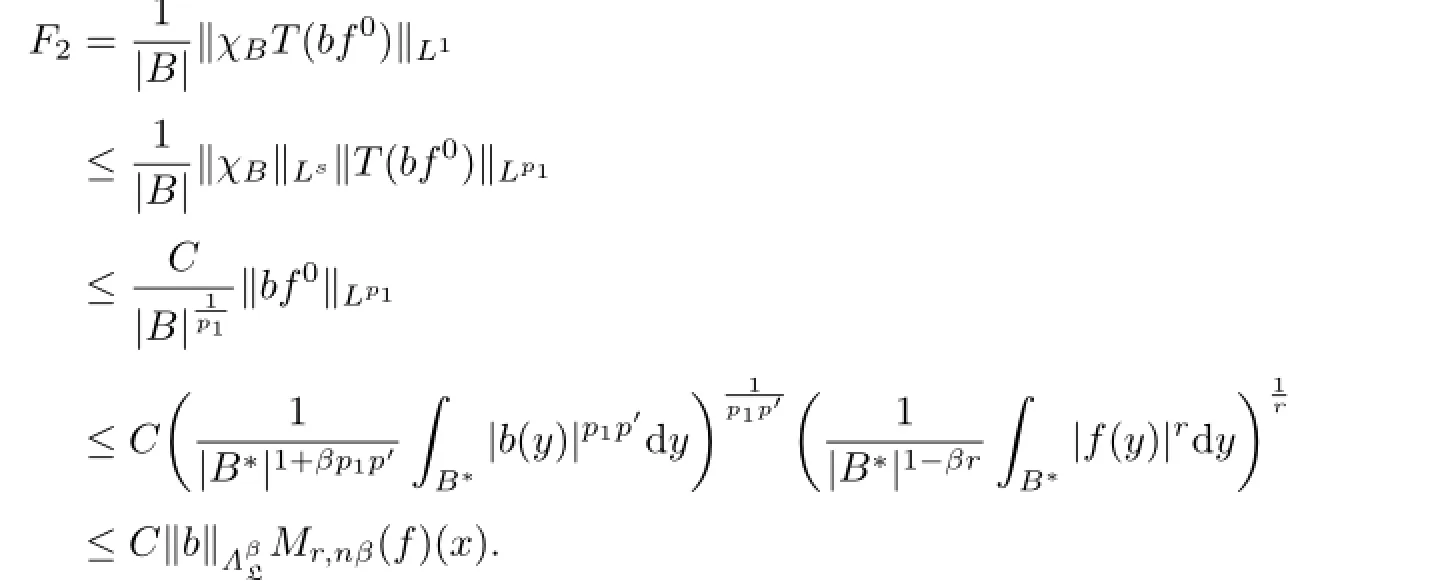
For F3,by using(1.3)and i＞0,

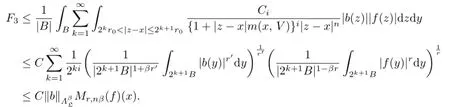
Combining the estimates for E1,E2,E3,F1,F2and F3,we conclude that

This completes the proof of Theorem 2.1.

Proof of Theorem 2.2

Without loss of generality,we can assume that 1＜r＜p＜p0.Sinceis dense in Lp(Rn),applying Theorem 2.1,Lemmas 1.1,2.1 and 2.2,we derive the inequality as

follows:

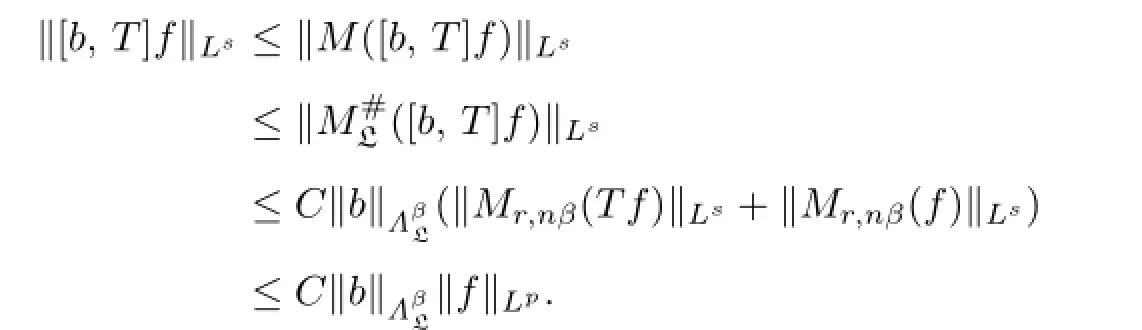
The proof of Theorem 2.2 is completed.

Proof of Theorem 2.3

Case I.We first show that for all x∈Rn,0＜r0＜ρ(x)and B=B(x,r0),there exists a constant C＞0 such that

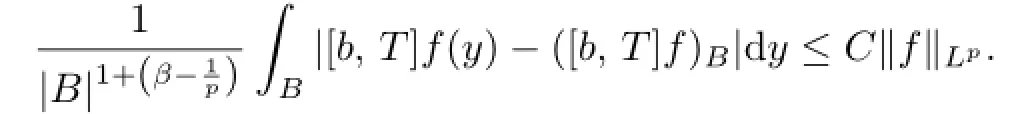
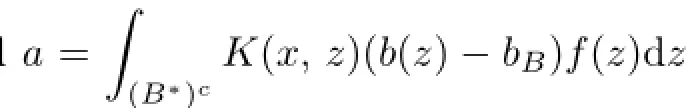
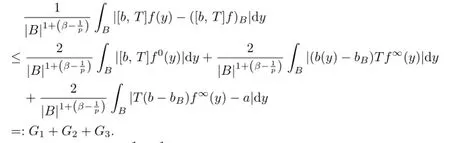
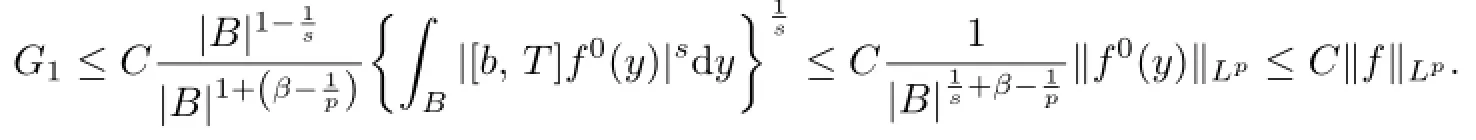
Applying(1.3),we have

From(1.4),it follows that

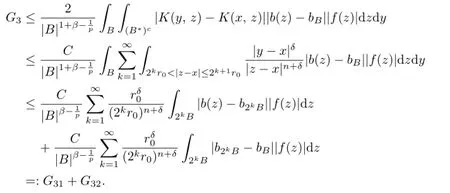
and

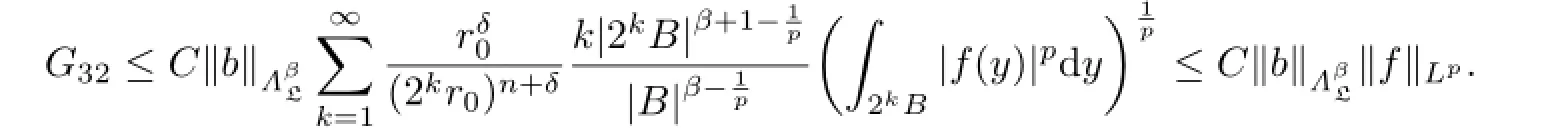
Case II.In the following,we show that for all x∈Rn,ρ(x)≤r0and B=B(x,r0), there exists a constant C＞0 such that

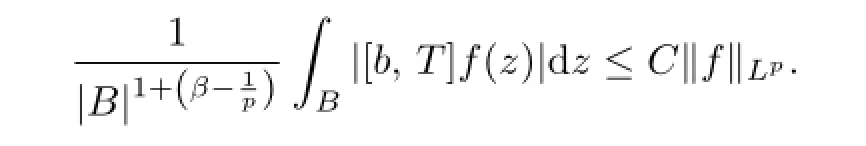
Take

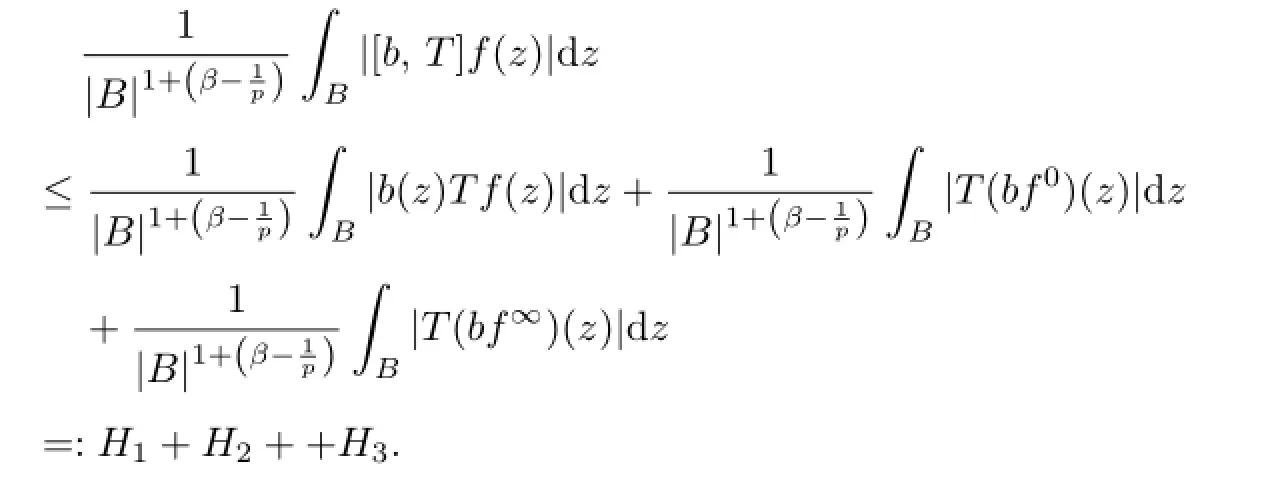
For H1,by H¨older's inequality

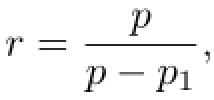
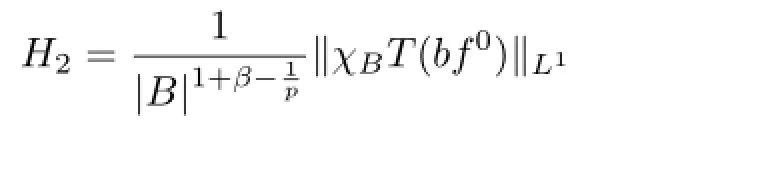
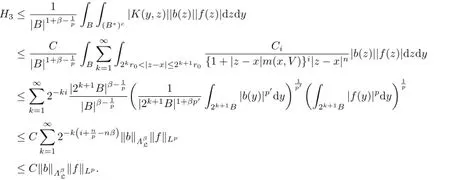
Thus,combining the Cases I and II,we complete the proof of Theorem 2.3.

[1]Fefferman C.The uncertainty principle.Bull.Amer.Math.Soc.,1983,9:129–206.

[2]Shen Z.Lpestimates for Schr¨odinger operators with certain potentials.Ann.Inst.Fourier (Grenoble),1995,45(2):513–546.

[3]Zhong J.Harmonic Analysis for Some Schr¨odinger Type Operators.PhD thesis.Princeton: Princeton University,1993.

[4]Guo Z,Li P,Peng L.Lpboundedness of commutators of Riesz transforms associated to Schr¨odinger operator.J.Math.Anal.Appl.,2008,341:421–432.

[5]Li P,Peng L.Endpoint estimates for commutators of Riesz transforms associated with Schr¨odinger operator.Bull.Austral.Math.Soc.,2010,82:367–389.

[6]Liu Y.Weighted Lpboundedness of commutators of Schr¨odinger type operators.Acta Math. Sci.Ser.A Chin.Ed.,2009,6:1091–1100.

[7]Bongioanni B,Harboure E,Salinas O.Commutators of Riesz transforms related to Schr¨odinger operators.J.Fourier Anal.Appl.,2011,17:115–134.

[8]Chu T.Boundedness of Commutators Associated with Schr¨odinger Operator and Fourier Multiplier.Master's thesis.Hunan:Hunan University,2006.

[9]Jiang Y.Some properties of Riesz potential associated with Schr¨odinger operators.Appl.Math. J.Chinese Univ.Ser.A,2012,7(1):59–68.

[10]Yang D C,Yang D Y,Zhou Y.Localized BMO and BLO spaces on RD-spaces and their applications to Schr¨odinger operators.Commun.Pure Appl.Anal.,2010,9:779–812.

[11]Yang D C,Yang D Y,Zhou Y.Endpoint properties of localized Riesz transforms and fractional integrals associated to Schr¨odinger operators.Potential Anal.,2009,30:271–300.

[12]Chanillo S.A note on commutators.Indiana Univ.Math.J.,1982,31:7–16.

A

1674-5647(2015)04-0289-09

10.13447/j.1674-5647.2015.04.01

Received date:Oct.31,2013.

The NSF(11161042,11471050)of China.

E-mail address:Huixmo@bupt.edu.cn(Mo H X).

2010 MR subject classification:42B20,42B30,42B35