感应电机电源切换中残压和电压差的研究及最优切换策略

崔学深 张自力 李和明 贾 英 张晓东

（华北电力大学电气与电子工程学院 北京 102206）

1 引言

三相感应电机在各种工业生产中得到了广泛的应用，常被用于驱动水泵、风机等生产机械，容量从几十瓦到几万千瓦不等。作为动力输出设备，其能否持续稳定运行往往影响着整个生产。感应电机突然断电，可能导致其驱动机械中断运行，危及其所在生产线的安全稳定，对一些不允许运行中断的生产来说，可能造成相当可观的损失。因此，重要生产均设有必要的备用电源，一旦供电系统出现暂时性故障或者线路定期检修等，就可以在短时间内将感应电机切换到备用电源上，从而保证了感应电机的不中断供电和重要生产线的持续运行。一般地，备用电源电压在幅值、频率上都与主电源电压相差不大，但其可能具有各种不同的初相角，基于此，本文仅讨论主备电源初相角不同时的感应电机电源切换问题，为描述方便，将幅值、频率均与主电源电压相同但具有不同初相角的备用电源简称为“不同备用电源”。

然而，当感应电机断电时间较长或者备用电源电压相位与主电源相差较大时，在电源切换中会出现很大的定子冲击电流和冲击转矩[1-4]，糟糕情况下，冲击电流可能高达额定电流的20 倍。较大的冲击电流会造成电网母线电压骤降，严重影响接在同一电网母线上其他负载的稳定运行（在舰船上尤为突出），此外，瞬态冲击转矩和电流也可能对电机的转轴和绕组造成很大的损伤。已有文献研究表明，解决感应电机电源切换冲击问题的有效方式主要有快速切换、同期切换和残压切换三种[5]，然而哪种切换方式最有利于抑制冲击问题，在什么时刻进行电源切换最有利，以往文献对此讨论较少，大多都是定性分析。因此，为了准确确定最优电源切换方式和最有利切换时刻，有必要进一步定量研究电源切换中感应电机定子残压及其与不同备用电源电压间的电压差和相角差特性。

有关感应电机断电过程和电源切换的研究，已有许多文献做了大量的工作，文献[6]认为由于电弧熄灭过程错综复杂，感应电机的断电过程可以有两种不同的处理办法，一种观点认为定子三相绕组与电源是同时断开的，另一种观点认为定子三相绕组不是同时断开的，并使用数值计算方法对断电过程和重合闸过程进行分析计算；文献[7,8]采用稳态等效电路来近似描述感应电机失电残压，初步讨论了残压的衰减规律以及其与电网电压之间的相位差问题，并介绍了几种常见的电源切换方式；文献[9-11]基于感应电机在ABC 或dq 坐标系统中的数学模型，对其失电残压和重合闸过程进行了分析和数值计算；文献[12]讨论了重要工业设备的自动母线切换控制系统，研究了电机断电后残压的幅值特性和母线切换方法；文献[13,14]假设电机断电后定子三相电流立即为零，使用空间矢量解析推导出定子残压的表达式，并简单讨论了残压对重合闸的影响。然而，这些文献在讨论电源切换中感应电机断电过程时，大都是假设断电后定子电流立刻为零，电机直接进入转子自由运动过程，与实际有所差别，影响定子残压的准确定量计算，此外有关定子残压与不同备用电源电压间的电压差和相角差特性研究较少。

基于以上内容，本文首先讨论感应电机与电源断开过程的处理方法，并根据断电过程中的定子电流实测波形，发现应该将电机断电过程分成定子两相不对称瞬态和转子自由运动两个阶段分别进行研究，才能与实际吻合；然后在不考虑电机转速变化下，使用感应电机对称、不对称空间矢量瞬态模型[15]，对其断电过程两个阶段分别进行深入的解析推导和计算，计算研究感应电机从主电源断电后定子残压的变化规律；其次，在假设备用电源电压幅值、频率与主电源相同条件下，解析研究具有各种不同初相角的备用电源电压与定子残压间的电压差和相角差特性，据此确定最优电源切换方式，并在考虑开关动作时间下准确确定最有利切换时刻，最后对其进行实验验证分析。

2 定子绕组断电过程的处理方法

由于所用开关的不同和电弧熄灭过程的复杂性，三相感应电机的断电过程常有以下三种处理方法：

（1）认为定子三相绕组与电源是同时断开的，也就是说，开关断开瞬间，定子三相电流立即同时变为零[6,8,13]，这种处理方法最简单，但不够准确，与实际有所差别。

（2）认为开关断开时，定子三相电流不能马上减到零，并假设每个电流是按指数规律进行衰减到零的[15]，这种方法实用性比较差，因为衰减时间常数难以确定。

（3）认为开关断开后，定子某一相绕组在其电流过零点时首先关断，余下两相绕组紧接着在其电流过零点时再同时关断[6]。

常用的开关有断路器、接触器、晶闸管和固态复合开关[17]等，其中采用DZ47—63 断路器将主电源从三种实验电机定子端切除，得到的定子电流实测波形如图1 所示。图1 中三种电动机的断电时刻是不同的，但是其断电过程呈现的现象是相同的，均可分为短暂的两相不对称瞬态和转子自由运动过程。此外，从图1 中还能看出，图1a、1b 两种情况中的一相绕组被断开近似发生在该相绕组电流过零点处，而图1c 中先被断开的绕组电流并不为零，但其断电过程出现的现象仍然和前者相同。由此可见，使用这种断路器控制电动机断电时，其实际断电过程与第三种处理方法最为吻合。实际上，使用晶闸管或固态复合开关切除电动机电源时其断电结果更是如此。基于这一事实，为了更加准确地定量计算感应电机断电过程中的定子残压及其与不同备用电源间的电压差和相角差特性，进而准确确定最优电源切换方式和最有利切换时刻，本文采用方法三来深入研究感应电机的断电过程。

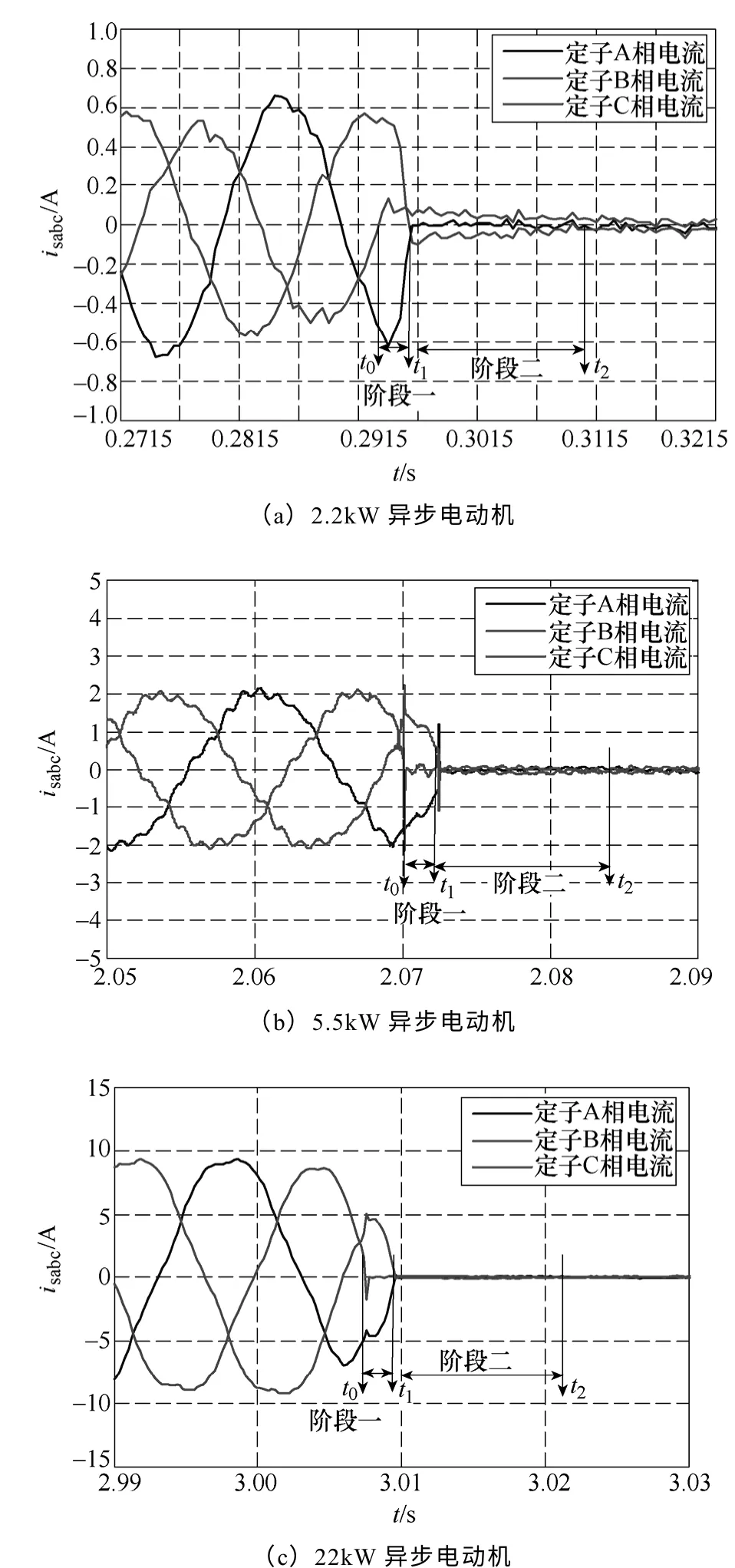
图1 定子断电过程中电流的实测波形Fig.1 Test waveforms of currents during the stator power-off process

考虑到感应电机和电源均是三相对称的，故断路器触头打开后，具体哪一相定子绕组先断开主要受断电时刻的影响，对电机断电过程的定量研究没有影响，在这里，以定子C 相绕组先过零关断为例，即图1a 所示的情况，显然可以将其断电过程分为两个阶段分别进行研究：第一个阶段从开关断开后定子C 相绕组电流过零关断时刻t0至余下两相绕组同时过零关断瞬间t1，此阶段较为短暂，为定子两相不对称瞬态过程；第二个阶段从时刻t1至感应电机进行电源切换瞬间t2，该阶段为转子自由运动过程。于是定子断电过程中感应电机的运行状态可用图2来展示。

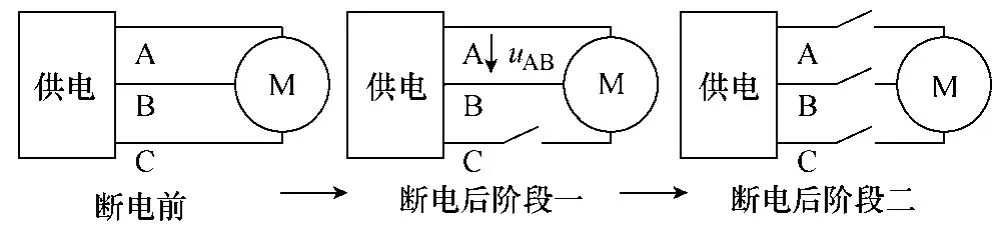
图2 断电前后感应电机运行状态示意图Fig.2 The schematic diagram of operation states of induction motor before and after the power off

3 感应电机对称及不对称空间矢量模型

根据前面分析可知，电源切换中三相感应电机的断电过程可分为定子两相不对称瞬态和转子自由运动两个阶段，以图1a 所示情况为例，结合图2可知，在对该过程进行定量解析计算时，需要用到感应电机的三相对称、两相不对称以及定子不接电源时的数学模型。

由文献[15,20]可以发现，对于恒速运行下的感应电机，使用空间矢量代替传统变量来建立感应电机对称、不对称模型时，能够有效降低感应电机对称、不对称模型阶数，这种模型阶数的减少能够大量简化电机模型的解析求解，特别适合解析研究感应电机断电后的短暂过渡过程。其中，在定子复坐标系中，感应电机三相对称运行时的空间矢量数学模为[18-20]

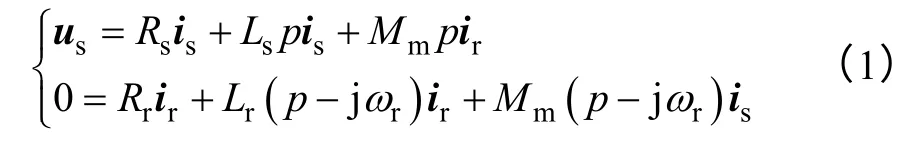
由文献[15]可知，当感应电机断电后定子C 相绕组先过零关断时，其定子A、B 两相连接着电源时的两相不对称空间矢量瞬态模型[15]为

式中 us——施加在定子端上的三相对称电源电压空间矢量；

uAB——电源A、B 两相间的线电压；

is，ir——定、转子电流空间矢量；

α=exp(j·2π/3)，其余参数和变量符号含义同文献[15]。

对于断电后处于阶段二的感应电机而言，其定子绕组与电源完全断开，定子电流为零，转子电流不为零，转子在转动惯性和负载作用下继续旋转并不断减速，转子电阻使得转子电流不断衰减，此时感应电机的数学模型为

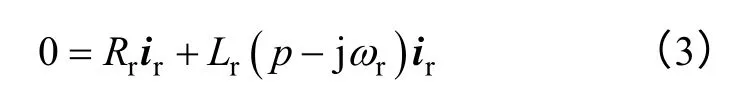
这时转子电流产生的磁场在定子绕组中所感应出的定子残压为

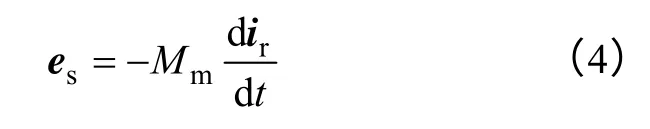
4 定子残压和磁链的解析推导

4.1 定子AB 两相不对称瞬态的解析

假设三相对称正弦主电源满足

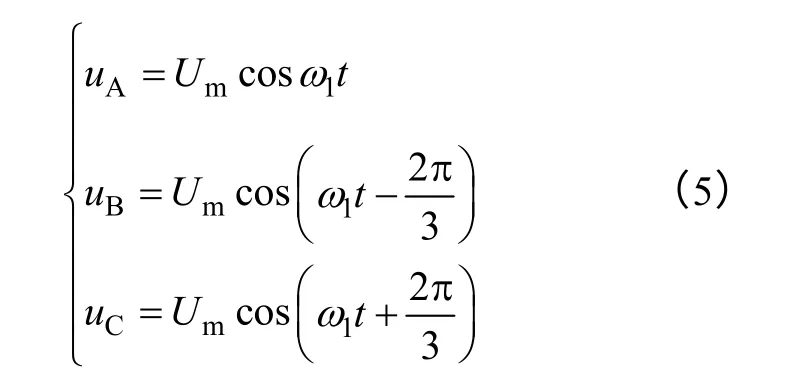
三相感应电机在 t=0 时刻接上主电源直接起动，至断电时刻t0（见图1a），该过程中电机处于对称运行状态。由式（1）和式（5）可以很容易地求出t0时刻瞬间前的定、转子电流空间矢量值。又断路器等开关切断电源时假设定子绕组过零关断，故可近似认为C 相断开前后定、转子电流保持不变，于是就确定了C 相断开后的定、转子电流空间矢量初值，分别假设为is0和ir0，再由ir0可以得到转子电流空间矢量的共轭分量初值。

此外，由式（5）可得，施加在电机定子A、B相间的线电压为

根据上述分析可知，断路器断开使得定子C 相绕组在时刻t0首先过零关断，这时感应电机定子A、B 两相绕组出线端仍与主电源相连接，感应电机从对称运行过渡到两相不对称瞬态，这时电机的运行行为可以用式（2）所述的空间矢量瞬态数学模型来定量描述。对重要工业应用而言，要求电机断电后迅速进行电源切换，因此断电过程时间短暂，而两相不对称运行阶段时间更加短暂，大约1/4 工频周期，故可认为断电后电机两相不对称运行过程中的转速ωr几乎不变。

结合式（6），对式（2）进行拉普拉斯变换，可得到一组线性常系数方程组，对其进行求解，求解过程同文献[15]中的案例分析，可以得到定、转子电流空间矢量的频域表达式，进而根据定子磁链和电流之间的关系式[19,20]为

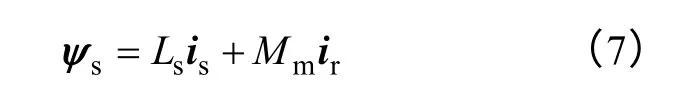
可求出定子磁链的频域表达式为

的特征根。对实验电动机而言，该方程有一个实数根和两个共轭复根[15,21]，分别记为

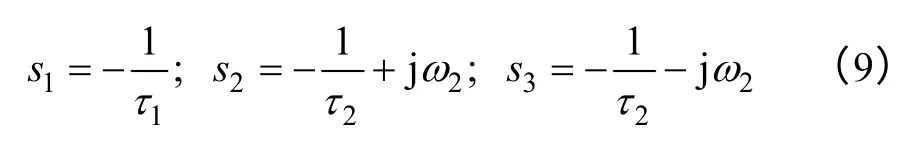
对式（8）进行拉普拉斯反变换，可求出定子磁链空间矢量的时域表达式为

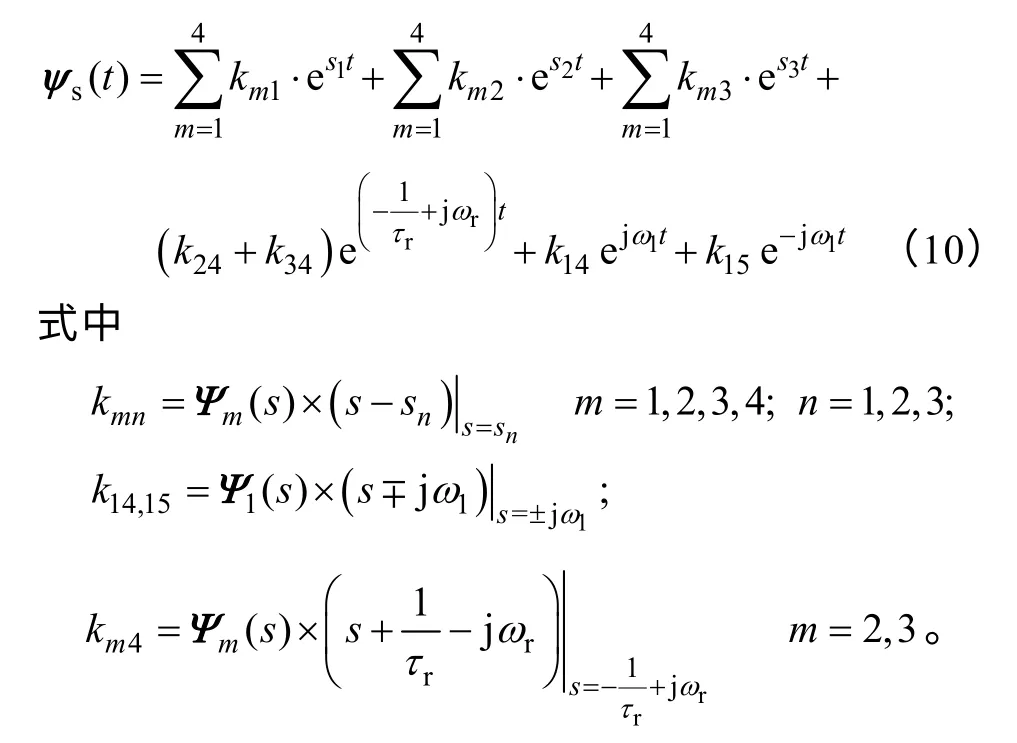
再根据法拉第电磁感应定律，可以得到电机断电后阶段一中的定子电动势空间矢量表达式为

以一台2.2kW 笼型感应电机为实验电机来进行研究，其定子绕组星形联结、无中线，主要参数为：UN=380V，IN=4.8A，Rs=6.928Ω，Rr′=7.369Ω，xsl=14.13Ω，Rm=36.25Ω，xm=486.7Ω，p=2，J=0.009kg·m2，F=0.001N·m·s。

对空载实验电机而言，定子C 相绕组电流过零关断后，电机从对称稳态运行过渡到两相不对称瞬态，根据上述解析结果进行计算，可得到极坐标系中定子磁链和电动势空间矢量轨迹，如图3 所示，图中红色实线为断电前电机处于对称稳态运行过程中的变量空间矢量轨迹，蓝色虚线为断电后电机处于阶段一（即两相不对称瞬态阶段）中的矢量轨迹。从图中可以看出，定子C 相绕组过零关断后，感应电机进入两相不对称瞬态阶段，该过程较为短暂；定子磁链和电动势空间矢量都略微减小，区别仅在于磁链是平滑的呈螺旋形减小，而电动势在定子C相绕组断开瞬间是跃变减小的，然后再平滑的减小。

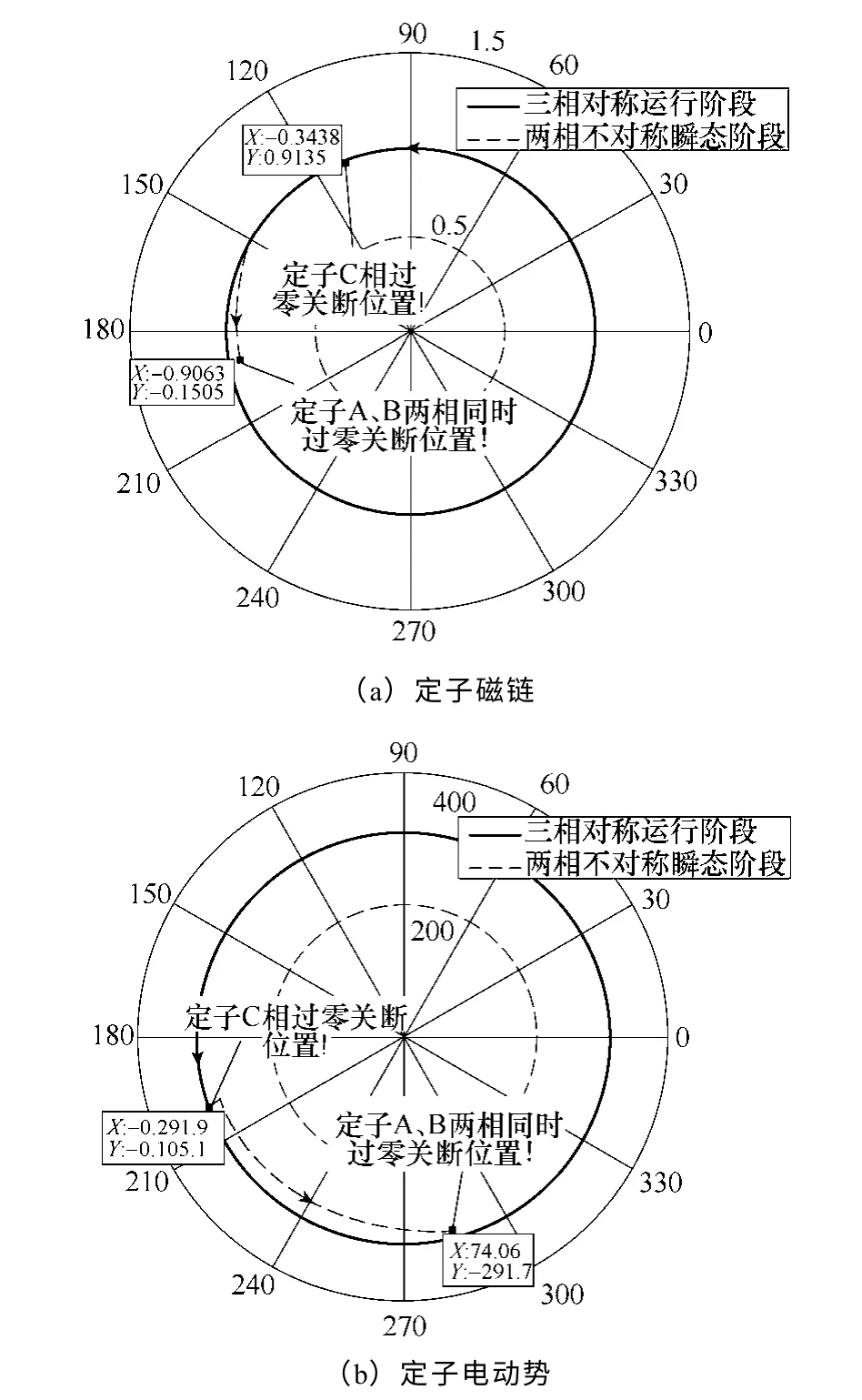
图3 过渡过程中定子磁链和电动势空间矢量轨迹Fig.3 Trajectories of stator flux and EMF vector during the transition

4.2 定子端不接电源时转子自由运动过程的解析

从图1a 中的t1时刻起，感应电机定子三相绕组完全与主电源断开，定子电流全部为零，而转子电流不为零，但由于转子电阻、转动惯性和负载的存在，使得转子电流逐渐衰减，此阶段为转子自由运动过程，可用式（3）所示的数学模型进行定量分析。

假设失电后阶段一所计算的转子电流终值为ir1，即t1时刻前的转子电流，其可认为是阶段二中转子电流的初值。结合式（3），可得转子电流为

值得注意的是，上式是针对电机某一恒定转速而言的，而实际上由于空载转矩和负载转矩的作用，断电过程中感应电机的转速在不断下降，对此，常有两种处理办法：①假设断电过程短暂且转动惯性较大，可认为电机转速几乎不变，这样转子电流就可以直接通过式（12）来描述；②如果断电过程较长，则认为电机转速下降，这时，可将阶段二分成若干个计算区间，每个区间足够小，以至于可认为电机转速在该区间内不变，每个区间计算之后，根据式（13）计算出一个新的电机转速，用于下一个区间的计算。

式中 p——电机极对数；

J——转动惯量；

TL——阻转矩；

Δt——所选区间对应的时间；

ωr(k)——当前区间内的电机转速，ωr(k+1)为下一区间内转速。

对于重要生产而言，要求电机断电后尽快进行电源切换，因此一般情况下断电过程较为短暂，此时可假设电机转速不变。这样，转子电流产生的磁场在定子中进行交链，所产生的残余定子磁链为

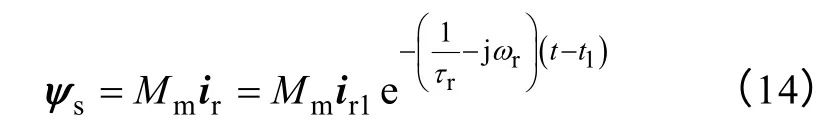
磁链交变，在定子绕组中感应出电动势，即所谓的残压为

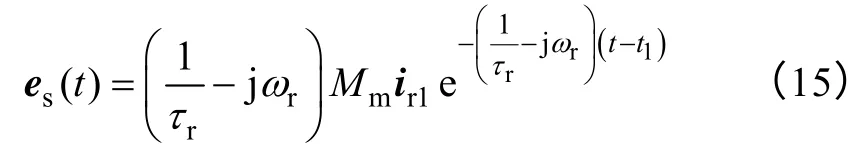
显然，该阶段是由初始状态引起的系统自由运动，对空载实验电机而言，根据上述解析结果能够快速计算求得定子残余磁链和残压，并可得极坐标系中它们的空间矢量轨迹，如图4 所示。

图4 定子绕组完全断开后磁链和残压的空间矢量轨迹Fig.4 Trajectories of stator flux and residual voltage vector after the thorough open of stator windings

从图4 中可以看出，感应电机断电进入第二阶段（即转子自由运动过程）后，定子中残余的磁链和电动势（即残压）均呈螺旋形平滑的减小，直至电源切换开始，抑或至两者均减小到零（即其轨迹螺旋地减小到极坐标原点）。

5 不同备用电源电压与定子残压间电压差和相角差的特性分析

本节在假设备用电源电压幅值、频率与主电源相同条件下，讨论具有各种不同初相角的备用电源电压与定子残压间的电压差和相角差特性，由此确定最优电源切换策略和最有利切换时刻，从而有效抑制电源切换中的冲击问题。

结合式（5），易得电机断电后即将接入的备用电源电压空间矢量为

式中，δ 是备用电源电压超前主电源的电角度，δ=0表示备用电源电压与主电源电压同相位，δ≠0 表示两电源相位不同，其大小代表两电源电压相位差的大小。

根据上文解析推导结果可知，感应电机断电后，不管是定子两相不对称瞬态还是转子自由运动过程，其定子残压均可写为以下形式

式中，A、B 分别为定子残压的幅值和相角，它们均是时间的函数，其解析表达式亦可以通过式（11）和（15）推导出来，为简单计，这儿不再具体列出，而是给出计算它们的一种简单办法。根据式（11）和式（15），可以解析计算出感应电机断电过程中每一时刻t 的定子残压空间矢量es(t)，再根据式（18）～式（19）分别计算出该时刻定子残压空间矢量的幅值A(t)和相角B(t)为

对空载实验电机，根据式（11）、式（15）、式（18）和式（19）进行计算，可得断电过程中定子残压空间矢量的幅值、相角特性，如图5 所示。从图中可以看出，定子绕组断电后，随着时间的推移，电动势幅值在不断的减小，相角变化周期在不断的增大，这主要是电机转子电流衰减和转速降低引起的。

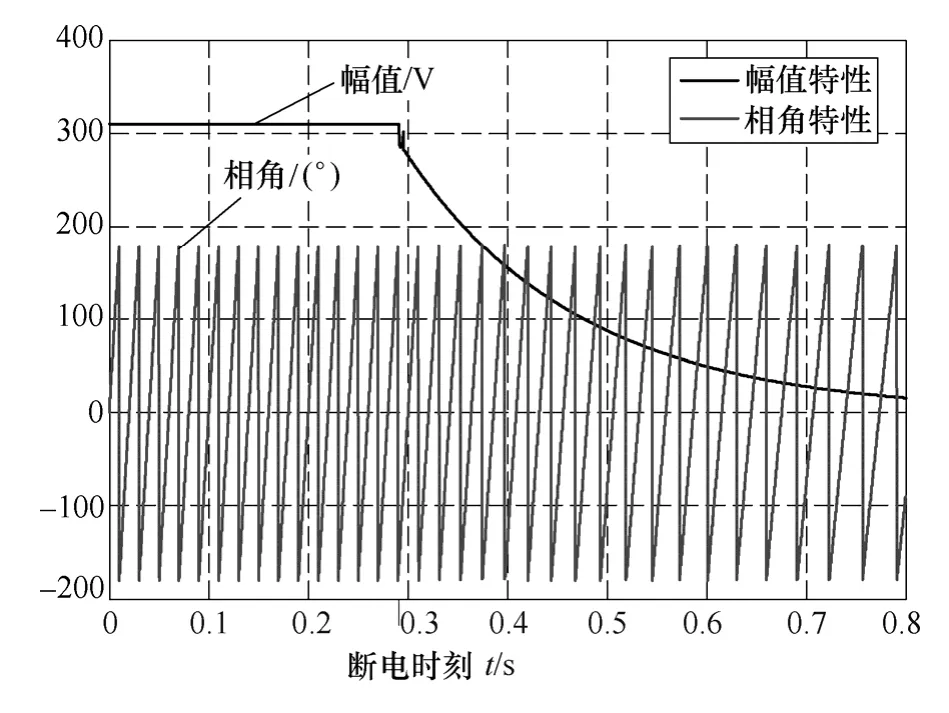
图5 定子电动势的幅值、相角特性Fig.5 Amplitude and phase-angle characteristics of the stator EMF

根据式（16）和式（17），可得不同备用电源电压和定子残压之间的电压差空间矢量为

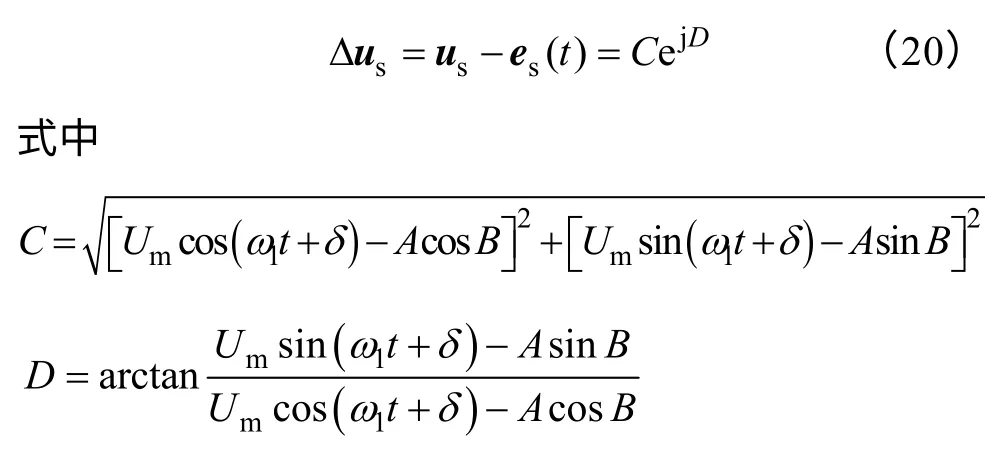
此外，由式（16）和式（17），可得不同备用电源电压和定子残压空间矢量之间的相角差为

式中，δ 可每取一个值，代表一种备用电源。

考虑δ=0°和δ=120°这两种不同备用电源，针对空载运行的实验电机，根据式（20）和式（21）进行计算，可得两种备用电源电压与定子残压间的电压差幅值特性和相角差特性，分别如图6 和图7所示，两图中还给出了前面所述的残压空间矢量幅值特性。从图中可以看出两种不同备用电源下的对应的电压差和相角差变化规律是不同的。在断电之前，两种备用电源对应的电压差和相角差均为恒值，但大小不同，就相角差而言，其大小分别为 0°和120°；断电后，两种备用电源对应的相角差均由初值缓慢增大至180°，这时备用电源电压与残压第一次反向，电压差出现最大值，然后相角差由-180°逐渐变化之0°，这时备用电源电压与残压同相位，电压差幅值最小，随后，转子转速下降导致相角差变化越来越快，电压差幅值也随之变化越来越快，最后，当电机转速下降为0 后，相角差按同步速变化，电压差幅值为备用电源电压幅值而不再变化。

图6 δ=0°时的残压、电压差及相角差特性Fig.6 The characteristics of residual voltage,voltage difference and angle difference when δ=0°

图7 δ=120°时的残压、电压差及相角差特性Fig.7 The characteristics of the residual voltage,voltage difference and angle difference when δ=120°

根据上述分析，并结合图6 可以发现，当备用电源与主电源同相位时，感应电机从主电源断电后，相角差由0 缓慢增大，电压差也由0 逐渐增大，显然这种情况下在主电源断开后越快进行电源切换越有利，即这种情况下快速切换最优，然而一般情况下考虑到开关快速性不足，不能实现最优电源切换方式，可以考虑选择同期切换，如果同期切换也不能成功实现时，则可以等待残压衰减至25%额定值以下时考虑实施残压切换，这三种切换方式及其对应的有利切换时刻见图6 中所标。用晶闸管开关代替普通开关，对空载实验电机在断电时间为 25ms和225ms 时分别进行电源切换，可得两种情况下的定子电流实测波形如图8 所示，其中断电时间25ms位于图6 中的I 区内，而断电时间225ms 对应图6中的W 点（为反向时刻）。从图8 中可以看出，当备用电源与主电源同相位时，在快速切换最有利时刻进行电源切换能够有效抑制冲击电流，而在备用电源与残压反向时刻对应的冲击很大，甚至比直接起动电流还大。

图8 δ=0°时，电源切换中定子电流实测波形Fig.8 Test waveforms of stator currents during the power switching when δ=0°

结合图7 可以发现，当备用电源电压超前主电源120°时，感应电机断电初期，备用电源电压与残压间的相角差较大，并很快出现反向这种最糟糕情况，且电压差幅值很大，显然这时不适合采用快速切换方式，但相角差很快又从-180°减小至0°，这时电压差幅值最小，在此刻进行电源切换最有利，即同期切换方式最优，其对应切换时刻见图7 所示，如果在此点不能成功实现电源切换，也可等待实施残压切换。一种通过晶闸管开关代替普通开关的空载实验电机在断电时间为20ms 和150ms 分别进行电源切换所测得的定子电流波形如图9 所示，其中断电时间20ms 对应图7 中的Q 点，该点对应相角差为127°，而断电时间150ms 则位于图7 中的同期切换有利时刻区域。从图9 可以看出，当备用电源与主电源相位相差较大时，不能实施快速切换，而在相角差第一次为零（即备用电源电压与残压同相位）时刻附近进行电源同期切换能够有效抑制冲击电流。

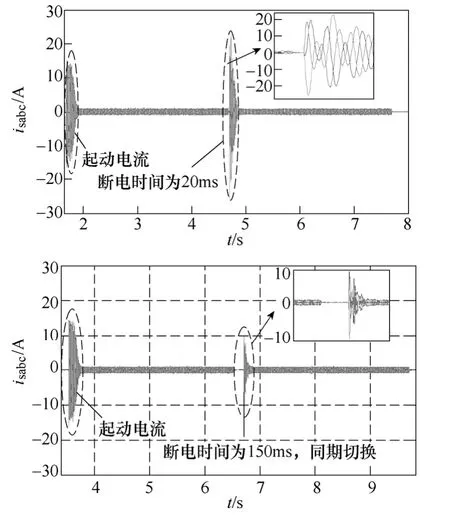
图9 δ=120°时，电源切换中定子电流实测波形Fig.9 Test waveforms of stator currents during the power switching when δ=120°

这儿需要注意的是，图8 和9 中所示电源切换中的定子电流实测波形，是使用晶闸管开关来实现电源切换的结果，其动作时间近似可以忽略，若使用断路器或者接触器，还需要考虑开关的动作时间。

6 结论

本文在假设备用电源电压幅值、频率与主电源相同且电源切换中电机转速不变条件下，基于感应电机对称、不对称空间矢量瞬态模型，对电源切换中定子残压及其与不同备用电源电压间的电压差和相角差进行了准确的定量研究，据此确定不同备用电源下的最优电源切换策略和最有利切换时刻，并取得以下结论：

（1）由电机断电后的定子电流实测结果，发现在电机进入转子自由运动过程之前，存在较为短暂的定子两相不对称瞬态过程，这种考虑有利于定子残压、电压差及相角差的准确计算。

（2）当备用电源与主电源电压相位差别较大时，同期切换最优，而当二者相位相同或者差别较小时，快速切换最优，但是一般情况下由于开关快速性不足，不能在最有利时刻实现快速切换，也可考虑使用同期切换，当快速切换和同期切换均未成功实现时，可采用残压切换方式，此外还需考虑开关的动作时间。

（3）用解析方法计算得到的残压、电压差和相角差，能够快速并准确确定最优切换控制策略。

（4）通过电源切换实测结果，验证了所预先确定的最优电源切换方式和最有利切换时刻是正确可行的，因此其具有工程应用价值，能够为电源切换中冲击问题的抑制研究提供理论参考和支持。

[1]Faiz J,Ghaneei M,Keyhani A.Performance analysis of fast reclosing transients in induction motors[J].IEEE Transactions on Energy Conversion,1999,14(1)：101-107.

[2]Beckwith T R,Hartmann W G.Motor bus transfer：considerations and methods[J].IEEE Transactions on Industry Applications,2006,42(2)：602-611.

[3]Yalla M V V S.Design of a high-speed motor bus transfer system[J].IEEE Transactions on Industry Applications,2010,46(2)：612-619.

[4]Das J C.Effects of momentary voltage dips on the operation of induction and synchronous motors[J].IEEE Transactions on Industry Applications,1990,26(4)：711-718.

[5]Higgins T A,Snider W L,Young P L,et al.Report on bus transfer.I.assessment and application[J].IEEE Transactions on Energy Conversion,1990,5(3)：462-469.

[6]高景德,王祥珩,李发海.交流电机及其系统的分析[M].北京：清华大学出版社,1992.

[7]Woudstra J B,Deleroi W.Re-switching of an induction motor with remainder flux[C].Third International Conference on Power Electronics and Variable-Speed Drives,London,1988： .

[8]Daugherty Roger H.Bus transfer of AC induction motors：a perspective[J].IEEE Transactions on Industry Applications,1990,26(5)：935-943.

[9]Shaltout A,Omoush M A L.Reclosing torques of large induction motors with stator trapped flux[J].IEEE Transactions on Energy Conversion,1996,11(1)：84-90.

[10]邓建国.三相异步电动机瞬间断电重合闸瞬态分析[J].电力自动化设备,2004,24(1)：37-41.Deng Jianguo.Transient analysis on reclosing of three-phase asynchronous motor[J].Electric Power Automation Equipment,2004,24(1)：37-41.

[11]Pillay P,Sabur S M A.Use of reduced order models to calculate reclosing transients in a refinery[C].Thirtieth Industry Applications Society Annual Meeting,Orlando,USA,1995,3：2180-2188.

[12]Hornak D L,Zipse Donald W.Automated bus transfer control for critical industrial processes[J].IEEE Transactions on Industry Applications,1991,27(5)：862-871.

[13]Cui Xueshen,Yang Yulei,Zhou Zhenhua,et al.The research on residual voltage of asynchronous motors and its impact on power restoration[C].Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies,NanJing,China,2008.

[14]高吉增,杨玉磊,崔学深.感应电动机失电残压的研究及其对重合过程的影响[J].电力系统保护与控制,2009,37(4)：45-48.Gao Jizeng,Yang Yulei,Cui Xueshen.The research of the residual voltage of induction motor after dumping and its influence during restoration[J].Power System Protection and Control,2009,37(4)：45-48.

[15]李和明,张自力,崔学深,等.晶闸管-电动机系统不对称瞬态建模及解析[J].电工技术学报,2013,28(8)：241-249.Li Heming,Zhang Zili,Cui Xueshen,et al.Asymmetrical transient modeling and analytical research of SCR-motor systems[J].Transactions of China Electrotechnical Society,2013,28(8)：241-249.

[16]B 阿德金斯,R G 哈利.交流电机统一理论[M].唐任远,朱维衡译.北京：机械工业出版社,1980.

[17]李卫国,罗应立,邱宇峰,等.高压固态切换开关在切换不同属性负载时的残压研究[J].中国电机工程学报,2013,33(15)：164-172.Li Weiguo,Luo Yingli,Qiu Yufeng,et al.Research on residual voltages of high-voltage solid-state transfer switch transferring different characteristic loads[J].Proceedings of the CSEE,2013,33(15)：164-172.

[18]汤蕴璆,张奕黄,范瑜.交流电机动态分析[M].北京：机械工业出版社,2008.

[19]崔学深.感应电机电源软投入相关理论及节能控制新技术的研究[D].北京：华北电力大学,2009.

[20]Novotny D W,Lipo T A.Vector control and dynamics of AC drives[M].New York：Oxford Clarendon Press,1996.

[21]罗炜,崔学深,罗应立.感应电机不对称暂态分析中一类一元三次特征方程及其近似求解[J].中国电机工程学报,2008,28(27)：126-130.Luo Wei,Cui Xueshen,Luo Yingli.Approximate solutions of a class of cubic characteristic equations in asymmetric transient analysis of induction machines[J].Proceedings of the CSEE,2008,28(27)：126-130.