感应电能传输系统电磁机构带通滤波特性建模分析

黄立敏 李砚玲 麦瑞坤 何正友

（西南交通大学电气工程学院 成都 610031）

1 引言

感应式电能传输（Inductive Power Transfer,IPT）是一种根据电磁感应原理，以松耦合方式将能量由电源侧发送到负载侧的新型技术[1]。这种无线传能方式相对于磁共振、电场耦合以及微波等其它能量传输方式，其优势主要体现在IPT 系统便于大功率能量传输，同时其控制和实现相对简单，且能量无线传输的距离能够满足实际应用[1]。对于非接触能量传输系统的定量分析方法，常用的研究理论主要有：①耦合模理论（Coupled Mode Theory,CMT），用于研究两个或多个电磁波模式间耦合的一般规律的理论，多见于磁共振式电能传输系统的分析研究之中[2]；②集总参数电路理论（Circuit Theory,CT），通过建立系统等效电路模型分析其系统特性，主要应用于电力电子拓扑分析及控制系统的设计及研究之中[3]；③带通滤波器理论（Band-Pass Filter,BPF），现有文献主要研究分析通过带通滤波器设计磁共振电能传输系统的方法[4-5]。

而在IPT 系统中，考虑其电磁机构工作在双边谐振状态时同样存在固有的带通滤波特性，本文主要采用带通滤波器的分析方法，通过建立IPT 系统中电磁机构的等效电路模型，研究IPT 系统中原、副边电压增益在电磁机构不同耦合状态下的带通滤波器特性，并针对这一特性给出基于上述滤波器分析方法的IPT 系统电磁机构设计指导方法。

2 电磁机构分析

2.1 电磁机构建模

常见的IPT 系统如图1 所示：输入电源在经过一系列的电力电子变换后得到高频交变电流，通入能量发射装置（原边线圈）后在空间中产生高频交变磁场，该交变磁场通过电磁感应耦合到能量接收装置（副边线圈）之后，得到交变感应电压，再次经过一系列的电力电子变换之后最终供给负载使用。其中，电磁机构是系统实现电能非接触传输的关键模块。

图1 IPT 系统原理框图Fig.1 IPT system principle block diagram

为研究IPT 系统电磁机构的能量传输特性，将图1 中的电磁机构简化为如图2 所示的等效电气原理图进行建模分析。

图2 IPT 系统电磁机构电路模型Fig.2 Circuit model of IPT electromagnetic mechanism

2.2 电磁机构磁通量分析

考虑电磁机构中能量传输通道的介质（磁芯及空气）均满足磁导率各向同性的特点，因此线圈中的磁通量与原、副边电流i1、i2大小成正比，系数分别是原边自感L1、副边自感L1、原副边互感M，其关系如表1 所示。

表1 IPT 电磁机构磁通量关系Tab.1 The relationship of flux in IPT electromagnetic mechanism

由于IPT 系统电磁机构工作于松耦合状态，即非理想耦合，存在漏磁通，因此在原边能量发射线圈的磁通总量Φ11中，可以记作以下两部分：其一是耦合在副边能量接收线圈中的磁通量，记为11Φ′ ；其二是只是经过原边线圈自身的漏磁通，记为Φf1。同理，对于副边能量接收线圈的磁通总量Φ22中，也存在两部分：Φ′22及Φf2。

2.3 电磁机构耦合系数

通过上述对 IPT 系统电磁机构中漏磁通的分析，定义机构耦合系数如下

分析可知，当电磁机构间为理想耦合时，其耦合系数接近1。然而对于IPT 系统而言，由于存在一定传输距离，电磁机构工作在松耦合状态，系统漏磁通无法避免，因此k 值远小于1，而且随着能量传输距离的增大，k 值将迅速减小，耦合系数k的设计不仅影响系统能量传递及系统效率，而且也影响着IPT 系统的稳定性，因此，k 值的选取也是IPT 系统电磁机构的设计标准之一[6]，以下的分析将从其原、副边电压增益的带通滤波特性出发，分析IPT 系统电磁机构间耦合系数k 值的选取。

3 带通滤波器特性分析

3.1 双边谐振电磁机构建模

在实际的IPT 系统设计中，通常在电磁机构原、副边线圈加入谐振补偿电容或电路[7]，使能量发射及接收装置均工作在谐振电路状态，从而实现电路的无功优化，提高IPT 系统能量传输功率等级以及效率。

对于加入谐振电容后的IPT 系统电磁机构，这种工作于双边谐振状态的电磁机构本身也构成了一种特殊的RLC 带通滤波器。

图3 含补偿电容的IPT 电磁机构电路Fig.3 Circuit model of IPT electromagnetic mechanism with compensation

考虑如图3 所示的原边机构采取LC 串联谐振补偿，副边机构采取LC 并联谐振补偿的非接触电能传输系统电磁机构，原、副边的耦合通过互感M表征，原边通入正弦激励源v1，选取适当的谐振补偿电容C1和C2，使原、副边两个电路均工作在相同谐振频率条件下，满足关系

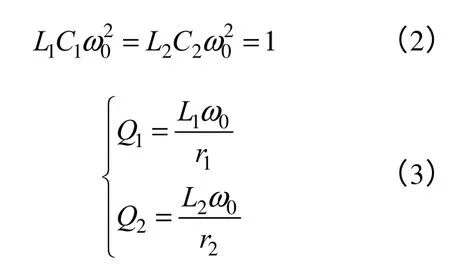
式中，Q1、Q2分别定义为发射装置及接收装置的品质因素；ω0为系统的谐振角频率，满足ω0=2πf0，f0为系统的谐振频率。

3.2 电压增益传递函数分析

为得到电磁机构能量接收装置以及能量发射装置之间的电压增益传递函数，列写原、副边电路的KVL 方程

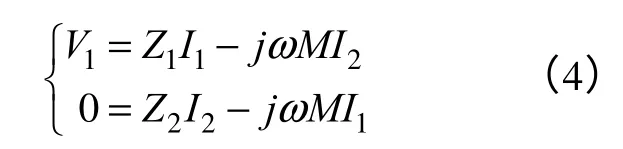
负载端得到的输出空载电压

考虑原、副边采用相同构造的装置，即满足：L1=L2=L 以及r1=r2=r，使其电感L 值及内阻r 均相等；此外，原、副边电路中的谐振电容也采取一样的容值C1=C2=C。在该种模型下，原、副边等效阻抗均由如下表达式给出

在此条件下，该系统电磁机构的输入、输出电压传递函数A(ω)表达式如下

在系统工作过程中，由于存在环境等不确定因素以及控制系统的调节作用，其电路实际工作频率存在微小频率摄动δ，定义为

其中，f为实际工作频率。在此条件下，电路阻抗Z 可近似表达为

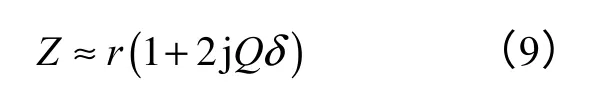
易知，当系统工作在谐振频率f0附近时，δ 趋近于0，且ω约等于ω0。因此可以构造新的频率变量，以衡量系统工作在微小摄动频率下的特性，令h=2Qδ，可得新的电压传递函数表达式如下

引入衡量电磁机构原、副边耦合程度的耦合指数n，定义为

对于两个几何构造确定的两个线圈装置，其Q值相对固定，而k 值的大小直接由其能量传输距离决定。因此，耦合指数n 可以作为具有一定几何机构的 IPT 电磁机构能量传输距离的设计指标及依据。将公式（11）代入式（10），最终可得化简后的IPT 系统电磁机构原、副边电压增益传递函数

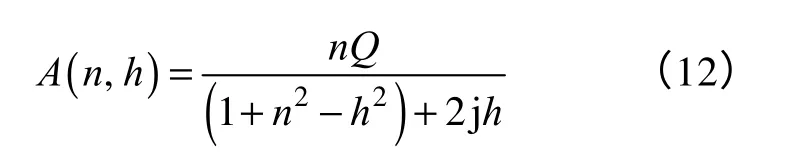
3.3 滤波频率响应分析

由式（12），可得当IPT 系统工作在谐振频率附近时，其电磁机构原、副边的电压增益模值表达式为

3.3.1 增益A 模值极值

为分析增益A 模值的极值，以h为变量对式（13）进行求导，数学上可知：当|A|达到极值时，满足

求解式（14），可得

由于h 是为关于f 的新频率变量，因此式（15）对应的实际系统工作频率为

对电磁机构的耦合指数进行n 分情况讨论，以分析该电磁机构的滤波特性，采用n≤1 及n＞1 的分段分析方式：

（1）n≤1。

当耦合指数n≤1 时，电磁机构工作在传统耦合状态，此时增益特性只存在一个极值点。由图4 可得当n≤1 时，|A|只有在满足h=0，即f=f0及n=1 时，达到极值点，此时工作频率即系统谐振频率。

图4 电压增益A 模值（n＜1）Fig.4 Mode of voltage gain A（n＜1）

（2）n＞1。

由图5 可得当n＞1 时，电磁机构工作在频率分叉状态，此时|A|存在三个极值点，从数学上分析这些极值点的种类，对增益模值求关于h 的二阶导数，有

可得，当系统工作在n＞1 的状态下时，工作在f=f0的状态下得到极小值，而在f=f1=f2时得到极大值。

图5 电压增益A 模值（n＞1）Fig.5 Mode of voltage gain A（n＞1）

因此，在设计IPT 系统电磁机构时应满足n=1或在1 左右，可让电磁机构满足电压增益较大的前提下呈现通带平坦的良好带通滤波特性。

3.3.2 主瓣最值

第一部分已经说明当n=1 时，|A|存在主瓣极值，则在h=0 时，电压增益主瓣的模值表达式如下

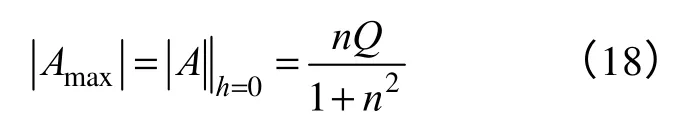
由图6 可知，当n=1 时，主瓣幅值存在极值Q/2，且当电路设计在n＞1 时，其增益主瓣幅值衰减迅速。为保证良好的电压增益效果应设计电磁机构的耦合指数n 在1 附近。

图6 电压增益主瓣模值与耦合指数n 的函数关系Fig.6 Voltage gain main lobe as a function of coupling index

3.3.3 旁瓣最值

当IPT 系统电磁机构设计为耦合指数n＞1 时，电压增益模值存在旁瓣最值，此时系统工作频率为次谐振频率时，分析可知旁瓣最值也是一个定值，且满足

4 系统设计实例

利用上述分析结果，基于IPT 系统电磁机构设计并仿真一套感应式电能传输系统，系统工作频率为f0=20 kHz，设计其电路参数如下：

C=307 nF,L=206 μH,r=1 Ω,Q=25

采用原、副边相同的电磁机构，模拟其在不同耦合条件下的电压增益带通滤波特性，如图7 所示：

图7 不同耦合条件下电磁机构的滤波特性Fig.7 Filtering characteristics in different coupling conditions

借助滤波理论进行分析，可以得出：当耦合指数n=1 时，电磁机构电压增益滤波特性的带宽约为1 120 Hz，此时电压增益达到最大值Q/2。

与此同时，传统的RLC 串联、并联谐振电路将只能得到带宽为800 Hz 的滤波器，因此，若采用基于IPT 系统电磁机构设计新式带通滤波器，也能在滤波效果上达到性能上的提升。

5 结论

本文通过建立感应式电能传输系统电磁机构的带通滤波器模型，分析得出对于相同的能量发射、接收装置，随着系统耦合强度的增强，即k 值的增大，系统的电压增益会降低，同时由于电路的频率摄动还会导致电压增益的剧烈波动。因此，引入耦合指数n 作为IPT 系统电磁机构设计指标，对于一定的能量发射及接收装置，在不同的工作频率下，通过调节能量传输距离改变系统k 值的方法，使耦合指数n 取值在1 附近，即可达到电磁机构的电压增益最大且波动小的设计目标。

本文在电磁机构的滤波器模型分析中，采用了相同构造的能量发射及接收装置，对IPT 系统的电磁机构进行了一定简化；此外，忽略了负载对电磁机构整体Q 值的影响，此两点均有待在接下来的研究中进一步完善。

[1]Covic G A,Boys J T.Inductive power transfer[J].Proceedings of the IEEE,2013,101(6):1276-89.

[2]赵争鸣,张艺明,陈凯楠.磁耦合谐振式无线电能传输技术新进展[J].中国电机工程学报,2013,33(03):1-14.Zhao Zhengming,Zhang Yiming,Chen Kainan.New progress of magnetically-coupled resonant wireless power transfer technology[J].Proceedings of the CSEE,2013,33(03):1-14.

[3]黄学良,谭林林,陈中,等.无线电能传输技术研究与应用综述[J].电工技术学报,2013,28(10):1-11.Huang Xueliang,Tan Linlin,Chen Zhong et al.Review and research progress on wireless power transfer technology[J].Transctions of China Electrotechnical Society,2013,28(10):1-11.

[4]Awai I,Ishizaki T.Design of "magnetic resonance type" WPT systems based on filter theory[J].Electr Commun Jpn,2013,96(10):1-11.

[5]Sun S,Xu D T,Liu Q S,et al.From Filter to mid-range wireless power transfer system[C].Proceedings of the 2012 IEEE International Symposium on Radio-Frequency Integration Technology (Rfit),F,2012.

[6]Zierhofer C M,Hochmair E S.Geometric approach for coupling enhancement of magnetically coupled coils[J].IEEE Transactions on Biomedical Engineering,1996,43(7):708-14.

[7]Hu A P,Hussmann S.Improved power flow control for contactless moving sensor applications[J].IEEE Power Electronics Letters,2004,2(4):135-8.