基于混合转子结构和悬浮力控制的新型飞轮储能用无轴承电机

李大兴 夏革非 张华东 李文龙

（国网冀北电力有限公司承德供电公司 承德 067000）

1 引言

储能系统在微电网中有非常大的市场前景，对电网的电能质量、电网稳定性以及供电可靠性都有很大的提升。飞轮储能系统是一种能量转换的储能装置，突破化学电池的局限，用物理的方法实现储能。和其他基于化学性质的储能技术相比，飞轮储能在微电网中具有广阔的应用前景。飞轮储能系统中，支承高速飞轮的轴承技术是制约飞轮储能效率和寿命的关键因素之一。磁轴承由于无机械摩擦、无噪声而被广泛应用。无轴承电机是一种磁电机，没有任何传统的轴承或磁轴承[1-4]。它的新颖之处在于转子悬浮力所需的电磁力是由主磁场自身产生的，而不是有独立的磁轴承产生。为了在主磁场中同时产生转矩力和洛伦兹力，需要专门设计所需要的定子和转子。目前已经出现的各种定转子结构中，还没有一个转子拥有一个大的转矩承载力和很好的可控洛伦磁力。

通过有限元对各种不同转子结构（笼式转子、磁阻转子、外嵌永久磁铁转子和内嵌永久磁铁转子）的无轴承电机转矩和磁悬浮力进行了比较性研究[5-6]，鉴于此，本文提出了一种新型的混合转子结构，目的是为了改进无轴承电机的转矩和悬浮力性能。根据得出的悬浮力模型，提出了一种新的悬浮力矢量控制策略。

2 不同转子结构的转矩和悬浮力产生机理

为了产生转矩和悬浮力，无轴承电机的定子有两套不同极对数的定子绕组。理论上，所有的交流无刷转子都能用于无轴承电机[7,8]。但是，为了得出哪一种转子结构能产生较大的转矩和悬浮力，因此有必要对不同转子结构的无轴承电机做一个比较。如图1 所示。

图1 无轴承电机转子结构Fig.1 Rotor structures of bearingless motor

通过有限元（FEM）方法研究了悬浮力大小，相对于四个参考转子的悬浮绕组电流。工作条件假定为：电机的气隙是相等的，都为0.6mm，转矩绕组的固定电流为0.45A。结果如图2 所示，鼠笼转子和磁阻转子分别有最大和最小悬浮力。对于PM转子悬浮力的承载力大致是一样的。

图2 不同转子结构悬浮力大小的比较Fig.2 Comparison of levitation forces for different rotor structures

在同样工作条件下，不同转子结构计算出的电磁转矩如图3 所示。结果显示无轴承电机PM 转子产生的电磁转矩比笼型和磁阻式转子电机的大。同时也可以得出悬浮绕组电流参数对转矩的影响是较小的，甚至可以忽略，对悬浮力控制来说是一个好的特点。

图3 不同转子结构的转矩大小比较Fig.3 Comparison of torque for different rotor structures

3 新型的混合转子结构

图2 和图3 的结果表明：对无轴承电机来说，外嵌式PM 转子是一个较好地选择，和其他的转子结构相比，其产生的转矩是最大的，悬浮力也是较大的。对于在转子和定子之间没有偏移的电机来说上面的结论是正确。事实上，由于各种原因转子和定子之间的偏移或多或少还是存在的。例如，如果空气气隙不等，在气隙小的一边将产生电磁吸力。为了研究偏移原因，用有限元计算出的转子不同偏移量的轴向力如图4 所示，从图4 中可以看出，径向力随着转子位移偏移量的增大而线性增加。为了使转子回到中心位置，悬浮绕组就需要一个大的电流。但是，永磁电机通过悬浮绕组电流产生的气隙磁通密度与通过永久磁铁产生的相比是较小的，主要因为悬浮绕组电流产生的磁通还要通过一个较大的气隙，这与空气气隙的数量和永久磁铁的高度有关。因此，仅仅通过增大悬浮绕组电流而使转子回到中心位置是很困难的。

图4 转子不同偏移量所受到的轴向力Fig.4 Radial force due to eccentricity

本文提出的新型无轴承电机的转子结构如图5所示。两个辅助转子铁心加到永磁电机的转子上，可以增大悬浮力。混合的转子结构拥有永磁电机和笼型电机的优点。

图5 新型无轴承电机转子结构Fig.5 A new rotor structure of bearingless motor

为了验证新型转子结构的有效性，图6 给出了不同转子结构当转子偏离中心0.05mm 时，径向力相对于悬浮绕组电流图。图6 中的四条曲线对应于下列四种不同情况：

1.无附加铁心的永磁电机，g0＝1.0mm；

2.有附加铁心且气隙长度相等的永磁电机（2lc＝15mm，gc=g0＝1.0mm）；

3.有附加铁心且气隙长度较小的永磁电机（2lc＝15mm，gc=0.8mm，g0＝1.0mm）；

4.有附加铁心且气隙小，气隙较小的永磁电机（2lc＝10mm，gc=0.5mm，g0＝1.0mm）；

从曲线1 可以看出，对于永磁电机仅仅通过增加悬浮绕组电流不能补偿径向力。由曲线2 和4 可以看出用附加的转子铁心或减小附加转子铁心的空气气隙来补偿径向力是有效的。

图6 不同转子结构径向悬浮力对比Fig.6 Comparison of radial forces for different rotor structures

4 无轴承电机悬浮力控制方法

新型结构的无轴承电机有四极三相转矩绕组和两极两相的悬浮力绕组，在x-y静止坐标系中，三相转矩绕组可以变换成等效的两相绕组。如果给四极和两极绕组提供频率相同的、对称的两相交流电流，则在x-y静止坐标系中，相电流可以表示成：

四极和两极绕组电流将分别产生两个气隙磁场。通过Maxwell张量法，转子表面的径向力可以计算出来，将该力沿转子表面合成，x与y方向力合成结果可以表示为：

系数k的大小由下面的方程决定：

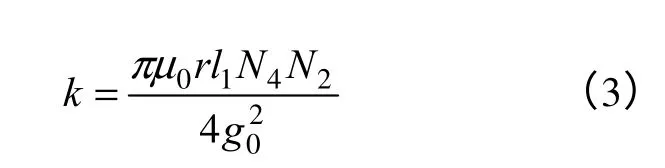
式中，N4和N2分别是四极和两极绕组每相的等效匝数；r、1l 及 g0分别为转子内半径，附加槽长度和气隙长度。由式（1）～式（4）可以得出x和y方向力的表达式为

由式（8）、（9）可以看出，通过瞬时定子电流可以计算出x、y方向的悬浮力。但是x、y方向力的大小取决于绕组电流。为了简化控制系统，最好减弱x、y方向绕组电流的相互作用。在x-y坐标系中相电流可以变换成d-q旋转坐标系中新变量，x-y参考坐标系与d-q参考坐标系转换电路如图7所示。两参考坐标中变量的关系式如下

如果i4放在d轴上，那么角度θ由θ=atan(i4y/ i4x)来决定，如图7所示。规定好i4的方向之后，由于i4和i2有相同的角频率，则d-q坐标系中的电流就变成直流成分，方程式（5）可以化简成：

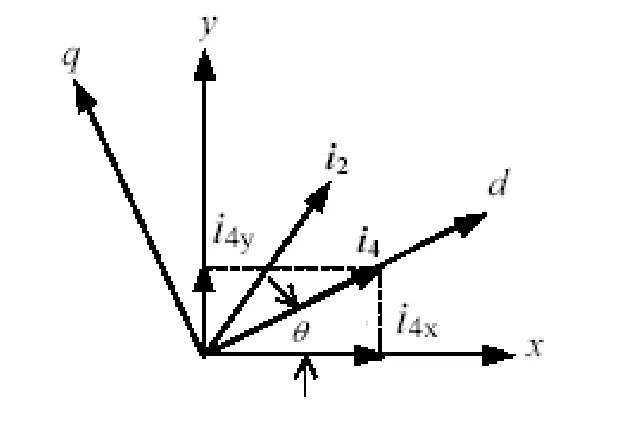
图7 xy 坐标与dq 坐标的转换关系图Fig.7 Transformation diagram of xy coordinate and dq coordinate

利用新变量，悬浮力的表达式可以简化为

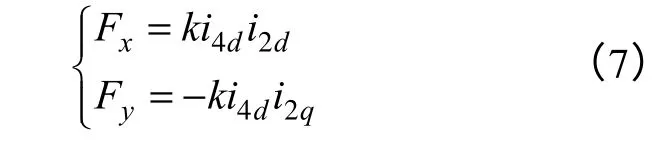
由式（7）可以得出，在同步旋转坐标系中悬浮力控制转换为对i2的控制。

5 实验结果

提出了基于DSP TMS320C32 和Xinlinx CPLD混和转子结构的无轴承电机控制系统，上述的悬浮力矢量控制也被应用。图8 和图9 显示了在速度达到750r/min 时，悬浮力矢量控制和无悬浮力矢量控制时转子的偏移量。每个图形的最顶端是由涡流传感器检测的x 及y 方向的转子偏移量。图8 显示的是无矢量控制，转子偏移量大，由于无悬浮力控制降低了轴承的利用率。在悬浮力的矢量控制下，转子偏移量较小，转子的悬浮情况如图9 所示。

图8 无转子矢量控制时转子偏移轨迹Fig.8 Rotor offset trajectory without vector control

图9 转子矢量控制时转子偏移轨迹Fig.9 Rotor offset trajectory with vector control

6 结论

提出的混和转子结构的无轴承电机不仅能产生大的电磁力矩和悬浮力，而且也实现了一种基于电流矢量的悬浮力控制方法。样机测试结果表明，新型无轴承电机的设计和控制策略是可行的。

[1]Okada Y,Miyamoto S,Ohishi T.Levitation and torque control of internal permanent magnet type bearingless motor[J].IEEE Transactions on Control Systems Technology,1996,4(5):565-571.

[2]Suzuki T,Chiba A,Rahman M A and Fukao T.An air-gap-fluxorientation vector controller for stable operation of bearingless induction motors[J].IEEE Transactions on Industry Applications,2000,36(4):1069-1076.

[3]Fang J C,Zheng S Q,Han B C.AMB vibration control for structural resonance of double-gimbal control moment gyro with high-speed magnetically suspended rotor[J].IEEE/ASME Transactions on Mechatronics,2013,18(1):32-43.

[4]Ren Y,Fang J C.High-stability and fast-response twisting motion control for the magnetically suspended rotor system in a control moment gyro[J].IEEE/ASME Transactions on Mechatronics,2013,18(5):1625-1634.

[5]Zhang W Y,Zhu H Q.Improved model and experiment for AC-DC three-degree of freedom hybrid magnetic bearing[J].IEEE Transactions on Magnetics[J].2013,49(11):5554-5565.

[6]Zhang W Y,Zhu H Q.Precision modeling method specifically for AC magnetic bearings[J].IEEE Transactions on Magnetics,2013,49(11):5543-5553.

[7]Darbandi S M,Behzad M,Salarieh H,Mehdigholi H.Linear output feedback control of a three-pole magnetic bearing[J].IEEE/ASME Transactions on Mechatronics,2014,19(4):1323-1330.

[8]李德广，刘淑琴.磁悬浮轴承数字控制的稳定性分析及预补偿算法[J].电工技术学报，2011，26(6):108-112.Li Deguang,Liu Shuqin.Stability analysis of the AMB digital control system and its predictioncompensatory algorithm[J].Transactions of China Electrotechnical Society,2011，26(6):108-112.