基于洞顶岩体应力传递的小型采空区稳定性评价方法研究

李国和

(铁道第三勘察设计院集团有限公司轨道交通勘察设计工程实验室，天津 300251)

基于洞顶岩体应力传递的小型采空区稳定性评价方法研究

李国和

(铁道第三勘察设计院集团有限公司轨道交通勘察设计工程实验室，天津 300251)

浅埋洞穴及小型采空区稳定性受顶板岩体结构强度、侧壁稳定性及上部荷载大小等多种因素影响，在地基稳定性评价中系统考虑这些因素的影响是保证评价结果真实可靠的关键。根据岩溶洞穴及小型采空区等地下空洞的分布特征，采用基于洞顶上方岩体应力传递的力学平衡分析方法进行洞穴稳定性评价，综合考虑空洞侧壁稳定和黏聚力c值的影响，推导临界深度计算公式，探讨了相关参数的取值方法。实例计算分析结果表明，本方法综合考虑洞穴侧壁稳定和黏聚力c值对洞顶稳定性的影响，使计算结果更符合客观实际，适于对浅埋洞穴的地基稳定性评价。

铁路；小型采空区；地基稳定性；评价方法

1 概述

目前，对浅埋洞穴及小型采空区地段的地基稳定性分析有多种计算方法，包括预计法、解析法、半预测半解析法及数值模拟方法等[1，2]。其中，力学解析法是目前洞穴及小型采空区稳定性评价中最常用的方法。在力学解析方法中，比较常用的计算方法有两种：一种是基于洞顶上方岩体应力传递的力学平衡分析方法；另一种是基于有界破裂区的计算。《铁路工程地质手册》[3]和《工程地质手册》[4]均推荐了第一种方法，即通过力学平衡分析方法，得出临界深度的计算公式，用以评价采空区建筑场地的适宜性。

应力传递实质上是洞室开挖后应力重分布，导致洞顶上方岩体受下沉力的同时又受到两侧岩体的夹持作用，即洞顶上方岩体卸载，而两侧岩体又对其加载。基于这一假定的计算方法目前多采用岩柱理论进行理论公式推导[5]。《铁路工程地质手册》给出了小型采空区地基稳定性计算的详细过程，首先对空洞顶板受力条件进行了一定的简化，并基于岩柱理论中松散体强度理论进行公式推导，在公式推导过程中，未考虑空洞侧壁稳定及黏聚力c值对顶板稳定性的影响。

根据众多资料，手册中推荐的洞顶岩柱力学平衡解析法在工程中得到了较为普遍的应用，尤其近些年在公路工程建设中对于小型采空区的评价[6]。如李满囤[7]研究了小煤窑采空区空洞顶板稳定性及临界深度问题，并将其应用到太古二级公路采空区治理中。刁心宏[8]等采用理论和半定量方法对昌金高速公路金鱼石路段路基下采空区的稳定性进行了评估，除采用力学平衡分析法外，还采用普氏塌落拱法及顶板坍塌自行堵塞估算法等半定量方法进行对比分析。向贤礼等[9]针对高速公路施工过程中遇到的路基岩溶地质情况，将定性、半定量方法应用到某高速公路岩溶路基的分析评价，其中所采用稳定系数法也是基于洞顶岩柱力学平衡分析的原理。近年来，采空区对铁路的影响也越来越严重，采空区稳定性评价工作逐渐受到重视，已有铁路工程技术人员将评价结论用于铁路的选线及设计中[10-11]。

根据对多处采空区稳定性评价的结果表明，对于顶板相对比较破碎的浅埋小型采空区，可忽略黏聚力的作用，但空洞侧壁的影响不可忽略，尤其对于那些埋深小但采高比较大的洞穴，采用手册中的评价方法得出的临界深度值会比实际小很多，因此，给工程留下很大的隐患。而对于顶板岩体完整性较好的洞穴评价，采用手册中提供的方法则忽略了黏聚力的作用，这样又会使评价结果趋于保守，给工程建设和洞穴治理造成不必要的浪费。综合考虑洞穴侧壁稳定及顶板岩体黏聚力的作用，采用基于洞顶上方岩体应力传递的力学平衡分析方法，对小型采空区地基稳定性评价公式进行了重新推导，并进行了实例计算分析。

2 理论分析

(1)相关手册的计算方法

对于埋深很浅的洞室，当采用岩柱理论计算时，洞顶压力等于上部岩层的全部重力，即

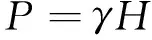
(1)

式中P——洞顶围岩压力；

γ——岩体容重；

H——洞室埋置深度。

当埋置深度加深时，岩柱除了自身的重力作用，还受到两侧岩体的约束，即夹持力的作用。洞顶岩柱受力分析见图1。

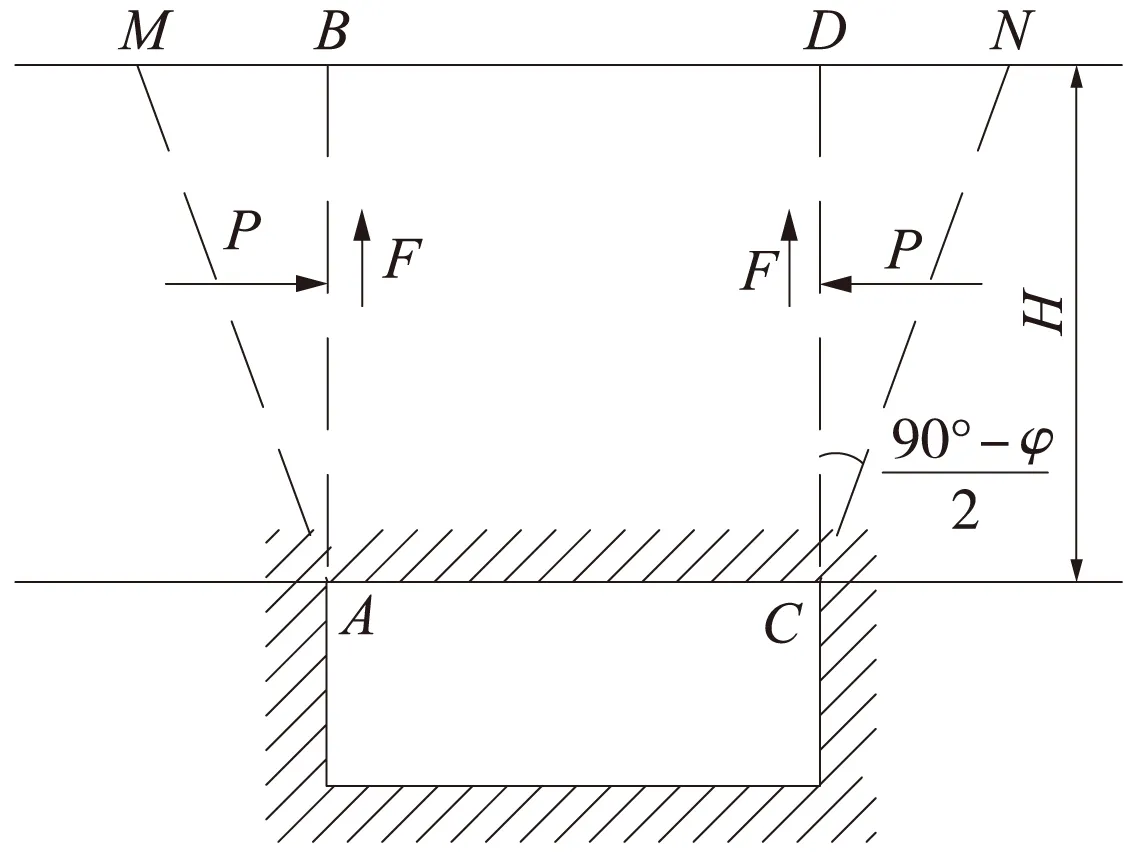
图1 洞穴顶部岩体应力平衡计算简图

根据岩柱理论，当洞穴埋深H增大到一定程度后，顶板上方岩柱的下沉力与夹持力恰好保持平衡(即洞顶压力P为0)而不塌陷，此时的洞穴埋深称为临界深度。基于上述假设，《铁路工程地质手册》中首先建立巷道顶板的压力P与深度关系H方程

(2)

进而计算顶板岩层自然平衡时的临界深度H0，用H与H0的关系来评价小型采空区的稳定性。其中，γ为岩层容重，2a为洞穴宽度，φ为内摩擦角。

(3)

当考虑建筑物基底压力R时，临界深度计算公式为

(4)

上述公式假定岩体面运动所发生的摩擦力τ=σtanφ，而岩体的黏聚力C=0。此时，利用上述公式计算临界深度H0会出现两种后果，首先，计算结果偏大；其次，φ值越大，H0随之增大，这与实际情况不符。在上述公式假设中，也未考虑空洞侧壁稳定性影响。当采高较大时，采用上式计算会导致计算结果偏小，即临界深度小于实际安全深度，为工程留下隐患。

因此，本文考虑洞穴侧壁稳定和黏聚力C值的作用，对上述公式进行了重新推导。

(2)力学模型分析及公式推导

当考虑侧壁稳定性和黏聚力影响时，受力形式如图2所示。

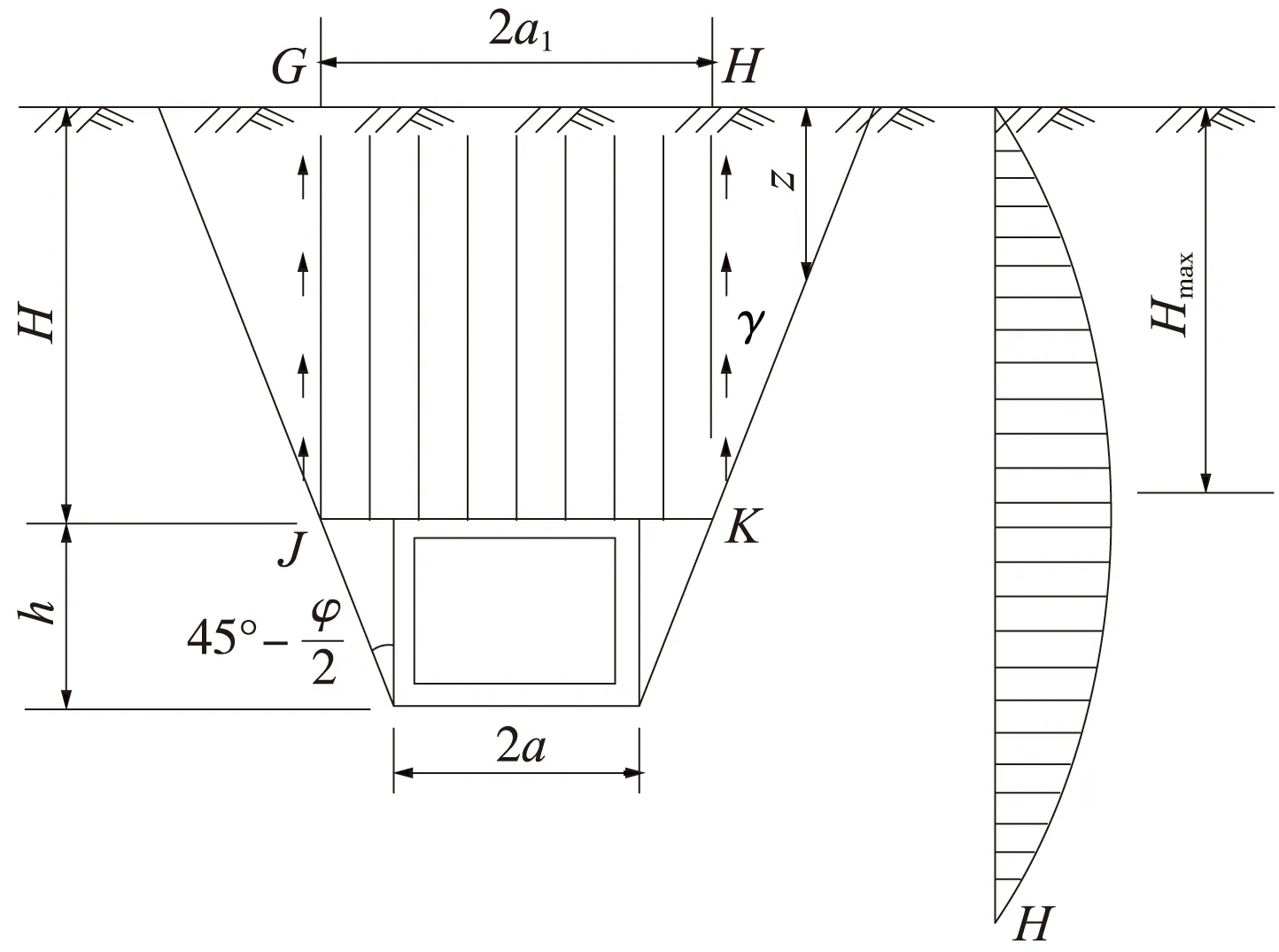
图2 考虑侧壁稳定和黏聚力的洞顶岩体应力平衡计算简图

考虑洞室两侧的岩体可能下滑，岩柱宽度适当增大，取侧向滑动面与垂直线的夹角按挡土墙理论取(45°-φ/2)。由此可以认为作用在洞室顶部的围岩压力等于岩柱的重量减去两侧滑动面上的摩擦力和黏结力。

(5)

距地面深度z处以上作用在岩柱侧面的夹持力(摩擦力和黏结力)强度为

(6)

式中，ez为距地面深度z处的主动土压力强度。

根据朗金土压力理论，当不考虑松散岩体黏聚力时，作用在墙体上的主动土压力强度为

(7)

考虑黏聚力时

(8)

取单位长度墙体(一般为1 m)，将式(8)沿深度积分，可得岩柱一侧所受到的总夹持力(总摩擦力和总黏结力)

(9)

当不考虑黏聚力时

(10)

当考虑黏聚力时

(11)

作用在洞顶的总围岩压力为

(12)

(13)

其中，G为沿洞室走向单位长度岩柱的总重力。

将式(10)和式(11)分别代入式(12)，即可得到作用在洞顶的围岩压力。

不考虑黏聚力时

(14)

考虑黏聚力时

(15)

根据上述公式，当深度增大，作用在洞顶的压力就会减小。当深度增大到一定程度，洞顶压力P为0，此时的深度H即为所要求得的安全深度，也称临界深度。

当不考虑黏聚力时，利用式(14)求得

(16)

当考虑黏聚力时，利用(15)式求得

(17)

考虑上部荷载Q时，将Q转化为沿岩柱表面均布荷载，荷载强度为q，则在单位长度岩柱表面上有

(18)

此时，作用在洞顶的总围岩压力为

(19)

将式(10)和式(11)分别代入式(19)，即可得到考虑上部荷载时作用在洞顶的围岩压力。

不考虑黏聚力时

(20)

考虑黏聚力时

(21)

(22)

将a1=a+h·tan(45°-φ/2)代入式(22)中得

(23)

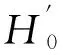
(24)

则有

(25)

解方程得

(26)

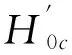
(27)

(3)计算参数选取

在上述公式计算中，土体C值和φ值可由钻探取原样试验得出，岩体C值和φ值有条件时可进行原位岩体试验得到。当无条件进行原位试验时，可参照相关手册根据岩体特征查表经类比分析来取值。《岩土工程试验监测手册》、《工程地质手册》、《铁路工程地质手册》等中均总结了国内外现场岩体抗剪试验部分成果。其中，在《岩土工程试验监测手册》[12]中详细列举了国内外一些典型工程岩石现场直剪试验数据，可供参数选择时参考。

《铁路工程设计技术手册—隧道》[13]中，收集了552组岩石和土体的野外抗剪试验及1422组室内抗剪试验所得到的C、φ值，经统计分析给出各类围岩的计算摩擦角(表1)。

表1 各级围岩计算摩擦角

在实际应用中，可先根据洞穴围岩主要工程地质条件确定围岩级别，再利用表1给出φ值。

3 实例验算

以某铁路经过的山东招远一小型金矿为例，采用上述方法计算临界深度。该矿矿床性质为花岗岩区热液成矿，当地称硫化矿。现场采样初步鉴定为黄铁绢英岩，矿物成分主要为石英、绢云母、黄铁矿和金等金属。围岩为花岗岩，局部蚀变成为绢英花岗岩。

(1)计算参数选取

矿脉平均厚3 m，倾角75°～80°，采空范围宽度平均3 m。根据现场调查及访问，巷道宽度1.8 m，高度2.0 m。采空范围沿矿脉延伸，最大宽度不超过4 m，高度一般为4 m，长为100 m左右。由于金矿采矿范围狭窄，属于小型采空。

分别对两处矿脉附近花岗岩取样进行岩石试验。岩-1节理裂隙较发育，岩-2相对较完整。岩石力学性质试验结果见表2。

表2 岩石试验结果

根据现场调查及岩石试验结果，确定岩-1取样点附近围岩为硬质岩，镶嵌结构。岩-2取样点附近围岩为极硬岩，整体块状结构。

在《岩土工程试验监测手册》中列举了国内外几个典型花岗岩地区水利水电工程岩体抗剪强度试验结果(表3)。现场试验数据表明，花岗岩体抗剪强度参数与岩体结构和风化程度关系密切，其中摩擦系数随裂隙发育程度及风化程度的降低而缓慢增长，而黏聚力却成倍增长。

表3 花岗岩现场直剪试验数据

参照表1和表3，岩-1附近岩体为硬质岩，裂隙较发育，围岩级别为Ⅲ级，φ值取55°，c值取200 kPa；岩-2附近岩体为极硬岩，结构较完整，围岩级别为Ⅱ级，φ值取67°，C值可取800 kPa。

(2)路基基底单位压力取值

填土高度按铁路设计断面取1.5 m，列车荷载按国铁Ⅲ级换算为土柱高度3.3 m，填土容重为18 kN/m3，则基底压力为q=86.4 kN/m2。

(3)计算结果分析

考虑不同的条件，对两处矿脉采空区的临界深度分别进行计算。计算参数见表4，计算结果见表5。验算结果表明，临界深度受洞穴跨度、洞穴高度、岩体抗剪强度参数、上部荷载等多因素影响。其中，洞穴跨度2a的影响最为显著。黏聚力C值和洞穴高度h的影响也相对较大。C值越大，H0越小，洞穴顶板越稳定。而h增大，H0也随之增大。

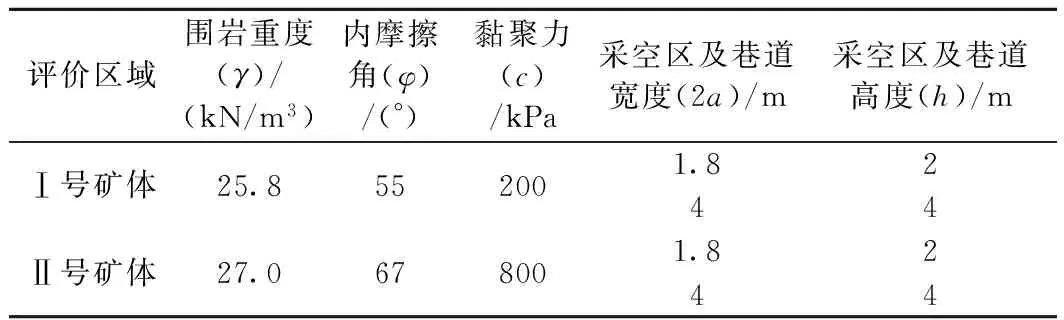
表4 采空区及巷道临界深度计算参数

表5 采空区及巷道临界深度计算结果

(4)地基稳定性分区评价

采用手册中提供的评价思路，根据H与H0的关系来评价浅埋洞穴及小型采空区地基稳定性。评价标准为：

当H

当H0

当H>1.5H0时，地基基本稳定。

采矿资料和现场调查结果表明，Ⅰ号矿体巷道及采空区顶板埋深约50 m，Ⅱ号矿体巷道及采空区顶板埋深约80 m。对比埋藏深度与临界深度的关系可以判定，Ⅰ号矿体内巷道地段地基基本稳定，采空区地段地基不稳定；Ⅱ号矿体内巷道地段地基基本稳定，采空区地段地基基本稳定。

根据评价结果，提出如下建议：(1)对Ⅰ号矿体采空区地段的铁路线路改线或对下伏采空区加固处理；(2)其他地段采取必要的监测措施。该铁路建设过程采纳了本文提供的评价结论和建议措施，经过十余年的成功运营检验，证实了本文提出的评价方法的合理性和可靠性。

4 结论

(1)本文基于洞顶岩体应力传递的基本假设，综合考虑洞穴侧壁稳定及顶板岩体黏聚力的作用，建立了基于洞顶上方岩体应力传递的力学平衡分析模型，并推导出浅埋洞穴及小型采空区的地基稳定性评价中的临界深度计算公式。

(2)通过实例分析，阐明了采用基于洞顶上部岩体应力传递方法进行小型采空地基稳定性评价的条件、步骤、参数取值方法及评价标准。

(3)本方法综合考虑了小型采空区侧壁稳定和黏聚力c值对洞顶稳定性的影响，适于对浅埋洞穴及小型采空区的地基稳定性评价。

[1] 童立元，刘松玉，邱钰，等.高速公路下伏采空区问题国内外研究现状及进展[J].岩石力学与工程学报，2004，23(7)：1198-1202.

[2] 郭广礼.老采空区上方建筑地基变形机理及其控制[M].徐州：中国矿业大学出版社，2002：5-47.

[3] 铁道第一勘察设计院.铁路工程地质手册[R].北京：中国铁道出版社，1999：387-391.

[4] 《工程地质手册》编委会.工程地质手册[R].4版.北京：中国建筑工业出版社，2007：574-575.

[5] 于学馥，郑颖人，刘怀恒，等.地下工程围岩稳定性分析[M].北京：煤炭工业出版社，1983：310-314.

[6] 孙宗第.高等级公路下伏空洞勘探、危害程度评价及处治研究报告集[M].北京：科学出版社，2000：1-474.

[7] 李满囤.太古公路采空区路桥稳定性分析及其治理方案[J].重庆交通学院学报，2000，19(3)：85-87.

[8] 刁心宏，刘峰，龚葛萍，等.高速公路路基下采空区稳定性评估与治理措施[J].华东交通大学学报，2006，23(2)：5-8.

[9] 向贤礼，曾祥忠.岩溶地区路基溶洞顶板的稳定性评价及应用[J].西部探矿工程，2007(6)：164-167.

[10]梁鑫，程谦恭，杨晓.含水率对采空区顶板稳定影响研究[J].铁道标准设计，2012(9)：15-18.

[11]何文春.高速铁路采空区桩板结构路基沉降数值模拟[J].铁道标准设计，2014，58(7)：15-19.

[12]林宗元.岩土工程试验监测手册[R].沈阳：辽宁科学技术出版社，1994：502-504.

[13]铁道部第二设计院.铁路工程设计技术手册·隧道[M].北京：人民铁道出版社，1978：32-33.

Study on Evaluation of Small Goaf Stability Based on Stress Transfer in Rock Mass

LI Guo-he

(The Third Railway Survey and Design Institute Group Corporation， Tianjin 300142， China)

The roof stability of shallow holes and small goaf are affected by many factors， including structural strength of rock mass， sidewall stability， upper load and etc. The foundation stability evaluation system in perspective of the influence of these factors is the key to ensure true and reliable evaluation. According to distribution features of karst caves， small gob and other underground cavities， mechanics equilibrium analysis based on the stress transfer of rock mass above the top of cave is adopted to evaluate the stability of cave with comprehensive consideration of the stability of side wall and the value of cohesive force. Calculation formulas for critical depth are deduced， and methods for related parameter selection are discussed further in this paper. The calculation results of project example show that this method takes into account comprehensively the stability of cave wall and cohesion values with computational results more consistent with the reality， and is suitable for stability evaluation of shallow caves.

Railway; Small goaf; Stability of foundation; Evaluation method

2015-03-11；

2015-04-03

李国和(1967—)，男，教授级高级工程师，2000年毕业于中国科学院地质与地球物理研究所，获地质工程专业博士学位，E-mail:guohe.li@163.com。

1004-2954(2015)11-0074-05

U213.1+4

A

10.13238/j.issn.1004-2954.2015.11.018