巧借“转换思想”攻克高中物理难题
袁亚琴

摘 要:解题教学是高中物理课程教学的重要内容之一,本文以高中解题教学为探究平台,从三个方面阐述如何将转换思想方法运用于物理解题中,进而体现转换思想在解题中的优越性和实效性,以飨读者。
关键词:转换思想;高中物理;解题教学
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2015)10-0052-2
在众多高中物理习题中,问题常常设置有多重障碍,运用常规的思维方法进行处理显得困难重重、力不从心。这就要求学生善于运用特殊的处理手段。在本文中,笔者采取理论与案例相结合的方式,重点阐述如何将转换的物理思维方法与策略巧妙运用于物理难题的处理中,以期对高中物理教学带来一定的参考与帮助。
1 巧借研究对象的转换,有效化解困难,促使学生思维“豁然开朗”
处理高中物理问题的首要问题是研究对象的确定。在具体的问题中,经常遇到一类问题:按照常规的思维方法对确定的研究对象进行处理,感觉十分困难,有时甚至无从下手,这时可以通过研究对象的合理转换,从而使难题“柳暗花明”。
例1 在粗糙的桌面上放置一块条形磁铁,如图1所示,在其右上方放置一垂直于纸面向里的通电直导线。当导线中电流强度增加时(磁铁相对于桌面始终保持静止),试讨论磁铁对桌面的压力与摩擦力的变化情况?
解析 本题中讨论磁铁对桌面的压力和摩擦力变化情况。从常规思维方法上考虑必须知道磁铁的受力特征,这里自然而然地选择磁铁为研究对象。磁铁受到电流的作用力分析起来十分困难(磁铁南极与北极同时受到电流的作用),基本是无法处理。这时如果将研究对象转换成通电直导线,问题就大大简化。如图2所示,当电流增大时,安培力增大,磁铁对桌面压力增大,摩擦力也增大。
点评 研究对象的选取是成功解题的关键。学生在对题目的处理中,往往都是比较定势地选取与待求量直接相联系的物体为研究对象,但是有时候这种方式解题比较困难,甚至于无法求解。此时,可以考虑进行研究对象的转换,让问题处理简化许多。
2 构造新旧模型之间的转换,排除解题策略困惑,体现“它山之石,可以攻玉”
利用物理模型处理问题是高效解题的重要途径之一,模型的运用能够简化思维过程,给解题带来方便。当然,在实际解题中,若构建的模型解题时比较繁琐,可以适当考虑进行关联模型的等价转换,从而实现快速解题的目的。
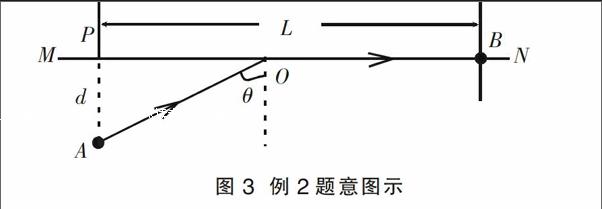
例2 在一次军事演练中的运动路径如图3所示,运输物资的汽车从出发点A至终点B,MN为平直公路,其余均为草坪。出发点A到MN的垂直距离为30 km,且A点在直线MN上的垂直投影与B相距120 km,汽车在草坪上行驶的速度为40 km/h,在平直公路上行驶速度为50 km/h。试求:汽车从A点运动至B的过程中的最短时间?
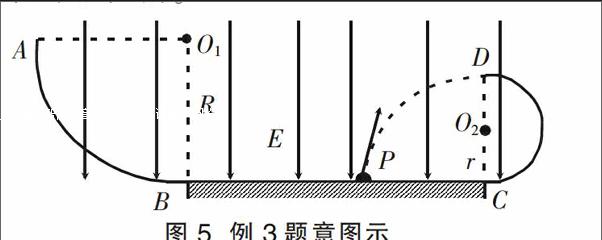
解析 本题是一道运动学问题,难点在于求最值。但是如果仔细分析汽车在草坪上和平直公路上运动速度关系:v1=40 km/h 根据光的折射定律可知:==,即sinθ=,得tanθ=。而OP=dtanθ=40 km,即OA==50 km。则t=+=1.85 h。 点评 高中物理课程教学内容涉及力、热、电、磁、光学等,它们之间存在着较大差异,但也有很多关联之处。很多问题本质上根本不同,但是在物理规律上却具有相同的特征。因此,在原有物理模型下处理问题比较复杂,有些问题甚至是无从下手时,这时可通过合理、有效的模型转换,从而使得难题“迎刃而解”。 3 突破常规思维下处理高中物理问题的困境,巧妙构建新思路,从而达到“峰回路转”的效果 利用物理知识、物理规律处理实际问题的过程中,多数学生都是按照常规的思维模式进行思考与分析,但是在实际操作过程中却发现部分题目解决起来过程复杂,出现错误的几率较高。这时可以突破原来的常规思路,构建新思路进行处理,往往会带来意想不到的效果。 例3 如图5所示,空间存在竖直向下的匀强电场,ABCD是竖直平面内的绝缘光滑轨道。质量为m,电量为q的带电小球从点P处斜向上抛出,恰好沿着水平方向从右侧半圆环(半径为r)最高点D进入,然后沿着轨道恰好能够到达左侧1/4圆环(半径为R)的最高点A。已知匀强电场的场强E=mg/q,试求:带电小球斜抛初速度的大小和方向。 解析 按照常规思路,考虑带电小球从P至A的运动过程,处理比较困难。这时不妨考虑采取逆向思维,将带电小球的运动等效成从A点静止释放沿着轨道运动至D点后做类平抛运动至P点,这样变换处理后问题变得通俗易懂、简明扼要;在A至D的过程中,利用动能定理可得: mv-0=(mg+qE)·(R-2r)即vD=, 在D至P的过程中小球做类平抛运动: mv-mv=(mg+qE)·2r即vP=。 在P点:vD/vP=cosθ,即cosθ=(其中θ为带电小球斜抛初速度与水平方向夹角)。 点评 利用常规的思路处理高中物理问题的过程中,有时会陷入意想不到的困境中,这时不妨考虑下转换解题的思路,另辟蹊径,探求新思路。 总而言之,高中物理一线教师在平时的课堂教学中应该注重学生创新思维能力的培养,在常规思想方法难以处理的复杂问题中,不妨改变思维模式,灵活机动地进行有效转换与变化,从而达到减负增效的目的。 参考文献: [1]邱引夫.物理模型转换的障碍及对策[J].物理教学探讨,2009,27(10):15—18. [2]陆红娟,李维兵.妙用转换法化解高考题中难点[J].物理教学探讨,2013,31(3):47—48. (栏目编辑 陈 洁)

