斯沃仿真软件椭圆类零件的切削与仿真加工

顾振宇

（永城职业学院，河南 永城 476600）

在零件程序编写过程中，我们经常会遇到公式曲线类零件，对于非圆曲线类零件，需采用直线逼近法进行逼近加工。一般来说由于直线法的插补节点均在曲线轮廓上，容易计算，编程也容易一些。采用直线逼近法加工椭圆类曲线，在零件轮廓编程时就需要使用宏程序进行编程。依据南京斯沃仿真软件进行仿真加工，模拟仿真椭圆类零件加工程序的编程过程，在数控编程与操作课程教学中具有指导意义。

1 椭圆类零件加工实例引入

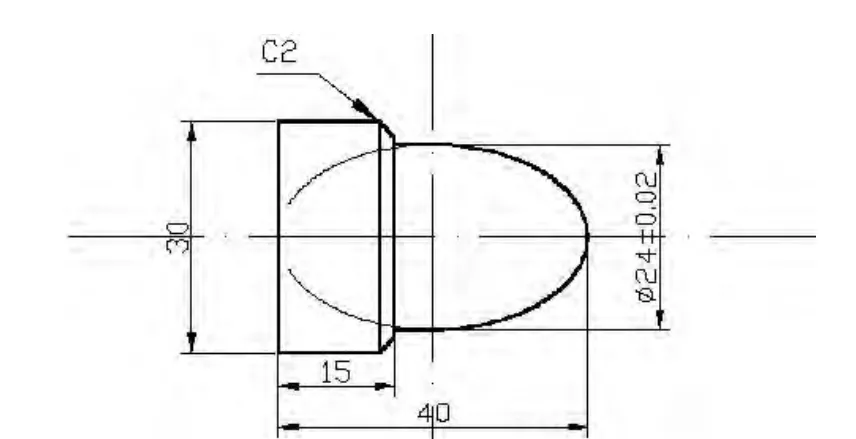
图1 椭圆类零件

如图1所示，应用宏程序编程对可以用函数公式描述的工件轮廓曲线进行数控加工，是现代数控加工中一个重要的新功能，但是使用宏程序编程用于数控加工公式轮廓曲线时，需要具有一定的数学和高级语言基础。对于上述椭圆类零件轮廓曲线的加工，首先要进行数学处理。椭圆方程为：X2/122+Z2/202=1;对于该类公式曲线，其中的X和Z坐标任意一个都可以被定于为自变量。对于车削加工而言， 一般选择 Z作为自变量。 则 X=

2 使用宏程序对零件轮廓进行程序编制

以零件右端面为零件编程坐标系零点，若选择以Z做自变量，则计算插补节点坐标即计算出在定义域D为[-20,0]。 把 Z赋给 #1；X赋给 #2，则 #2=sqrt[1-[#1*#1]/400]*12。由于所建立的编程坐标系零点与椭圆的中心并不一致，则对应于编程坐标系而言，对于编程坐标系而言把Z赋给#3，则#3=#1-25；又由于对于前置刀架数控机床而言，采用Fanuc oi系统进行编程时，X方向一般采用直径编程，所以把X的直径坐标值赋给#4，#4=2*#2。

编写程序如下：

其中参数设置如图2所示，仿真刀路轨迹如图3所示

图2 参数设置

图3 仿真刀路轨迹

3 椭圆类公式曲线零件铣削加工

在数控铣床上通过标准方程加工椭圆都是加工局部，最多一半，而第Ⅰ、Ⅱ象限或第Ⅲ、Ⅳ象限内可以一次加工的，若是要完整加工一个椭圆轮廓，必须要分为两次编程进行仿真加工。而使用参数方程进行宏程序编制加工椭圆类零件轮廓时，可以加工任意角度的椭圆轮廓，即使是完整的椭圆也不再需要分两次进行编程，直接通过参数方程编制宏程序加工即可。

参数方程为：x=acosθ,y=bsin X2/122+Z2/202=1,θ缀[0°，360°]如图 4 所示。

图4 整椭圆轮廓曲线

对于整椭圆类轮廓而言：如，X2/302+Y2/202=1,则对应参数方程为x=30*cosθ,y=20*sinθ。对于程序如下：

其中加工仿真刀路轨迹如图5所示。采用参数方程加工椭圆类轮廓曲线时，可以使用扩大刀具半径去除加工余量。

图5 参数方程仿真刀路轨迹

通过论述机床编程中使用到的公式曲线法和参数方程法进行宏程序编程，采用斯沃仿真软件进行仿真验证，有效解决了曲线类零件轮廓的编程问题。针对不同的数控系统,宏程序在编制时参数并不一样,但是原理大同小异。实践证明,上述方法简便、实用、有效,能够很好的加工出复杂的公式轮廓曲线。

［1］耿金良.数控编程与操作实训教程［M］.北京：中国传媒大学出版社，2010.

［2］苟维杰.数控机床［ M］.长沙：国防科技大学出版社，2009.