翼型摆角对气动性能的影响分析

季 康， 李 春，2， 叶 舟，2， 杨 阳

（1.上海理工大学 能源与动力工程学院，上海 200093；2.上海理工大学 能源与动力工程学院 上海市动力工程多相流动与传热重点实验室，上海 200093）

风力机在目前已建成的旋转机械中直径最大，然而随着单机功率的增加，其叶片长度也随之越来越长，这就会引起风轮叶片的弯曲变形，最终导致气动性能的变化［1］.研究表明，当风力机叶片长度增加至30m 以上时，叶片会产生柔性特性，再加上叶片本身材料的强度较高且模量较低，其几何非线性特性将会明显变强；而当叶片长度增加至60 m 以上时，尾缘由于同时受到气动力和结构力，在时域范围内会出现截然不同的非定常特性［2－3］.

近年来，对翼型尾缘摆角的研究主要集中在飞行器方面，然而对于风力机方面的研究相对偏向于叶片材料及控制等方面［4－9］.1999年，Andrew 等［10］第一次将主动控制变形叶片技术应用在风力机叶片上，其对变形叶片的研究重点在于不同弯扭结合的叶片设计方式，而不改变叶片的整体结构，文献［11－14］给出了新型适应性叶片，主要将叶片展向进行了适当的弯扭设计，但是并未涉及翼型尾缘变形后引发的气动效应.

本文选取NREL S809 翼 型［15］，通 过 数 值 模 拟商用软件研究不同攻角、来流风速和尾缘角度对其气动性能的影响，并对比变形翼型与原始翼型的升阻力系数及流线图，分析了变形翼型上下表面压力分布的变化规律.

1 尾缘变形翼型创建原理

对S809翼型尾缘进行变形，在弦长75%的后方，对翼型尾部进行摆动，如图1所示.定义5种翼型，分别为上摆－5°、原始翼型、下摆5°、下摆10°、下摆15°.

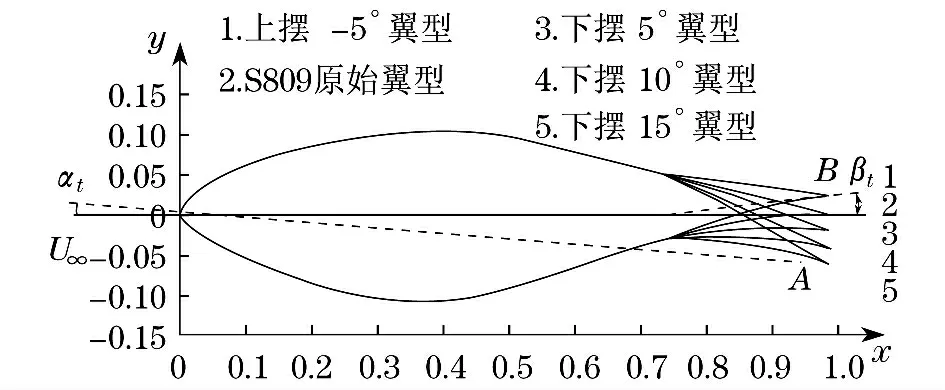
图1 翼型尾缘摆角及变形示意图Fig.1 Schematic diagram of pendulum angle and deformation of airfoil

在来流方向速度U∞不变的情况下，翼型尾缘的上下摆动改变了原始翼型的弦线，因而会对攻角αt产生一定变化，因此，假定尾缘向下摆动为正，向上摆动为负，其中，βt为尾缘相对原始翼型的摆动角度.

在尾缘1／4处，设定摆动角度βt变形规律为

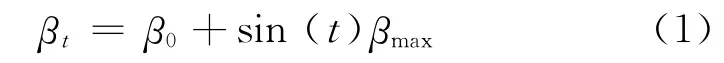
式中，β0为原始翼型摆角，即β0＝0；βmax为尾缘最大摆角；t 为摆动时刻.

利用二次函数来约束并形成尾缘部分的中弧线.

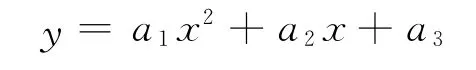
式中，x，y 为翼型弦长c 的坐标位置；a1，a2，a3为系数.

为了得到不同摆角下的翼型，可以通过以下约束条件来确定：a.A（xA，yA）与B（xB，yB）分别为尾缘中弧线的起点与终点；b.A 点始终保持与中弧线相切，斜率y′A＝k；c.且kAB—＝－tan（β0＋βt）；d.保持弧长不变.

根据上述条件可以得到如下方程：

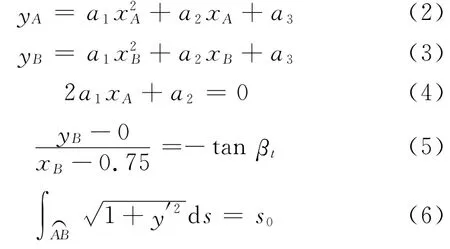
式中，s0表示原始S809翼型尾缘中弧线弧长.

如图2所示，假设来流为水平流动的风速.AB即为原弦线75%的后方，尾缘发生变形部分.OB 表示由于尾缘摆动变形后形成的新弦线.其中，βt 即表示翼型尾缘摆动的角度，αt表示翼型变形后的实际攻角.

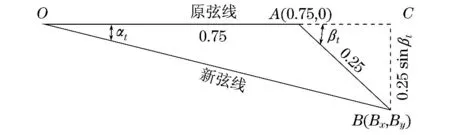
图2 翼型摆角βt与攻角αt关系简化示意图Fig.2 Simplified schematic diagram ofβtandαt

显然，当βt＝0时，原弦线和新弦线重合，αt＝βt＝0.当βt≠0时，OC＝0.75＋0.25cosβt，BC＝0.25sinβt.

由于尾缘变形而产生了新的弦线，攻角也随之产生了变化.

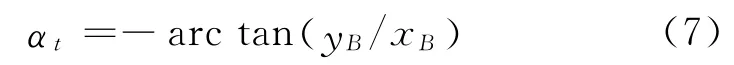
最终，βt与αt之间存在着一定的函数关系，其近似表达式为

由式（8）可知，翼型尾缘摆角与攻角的变换关系如表1所示，尾缘摆角每改变5°，相应的攻角改变约1.25°.在本文中，攻角表示来流风速与变形产生的新弦线之间的夹角，向上表示正摆角，向下表示负摆角.

表1 尾缘摆角角度与攻角之间的对应关系Tab.1 Relationship between pendulum angle and corresponding angleofattack

2 计算与结果分析

2.1 网格划分与计算条件

S809原始翼型流场计算域如图3所示.计算域主要由两部分组成，分别为上游来流和下游尾迹区.上游来流区是C型区域，半径为10倍的弦长；下游尾迹区是正方形区域，其边长为20倍的弦长.

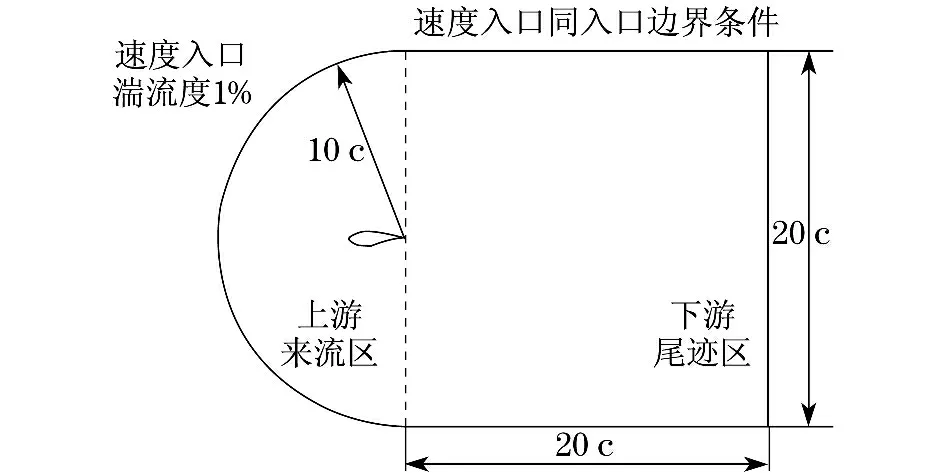
图3 流场计算域示意图Fig.3 Schematic diagram of flow field calculation domain

网格质量的优劣对数值计算有着关键性的影响，对于不同的计算工况，计算域的离散方法可以分为两类：非结构化和结构化网格.计算域整体网格分布如图4（a）所示，由于在翼型前缘与尾缘附近的压差变化较大，为捕捉翼型边界层附近的流动，在翼型周围布置边界层网格，如图4（b）所示.网格划分为结构化网格布置，第一层网格尺度为0.001m，计算域网格总数为50 000.

图4 计算域网格划分Fig.4 Mesh of calculation domain

边界条件的设定：a.入口边界设定为风速恒定的稳态风，湍流度选取1%；b.出口边界采用总压为0的压力出口；c.壁面条件采用无滑移条件；d.湍流模型 采 用S－A（Spalart－Allmaras）模 型，雷 诺 数 取7.5×105.

2.2 可靠性验证

为了验证上述计算模型及边界条件的可靠性，选取S809原始翼型，将其升阻力计算结果与实验值进行比较.本文中采用了OSU（Ohio State University）实验［16］的雷诺数为7.5×105时的S809 翼型实验数据作为二维静态测试数据.

图5是利用上述网格及边界条件，通过Fluent模拟出的原始翼型的静态升力系数CL与阻力系数CD在不同攻角（－6°～18°）下的变化趋势.

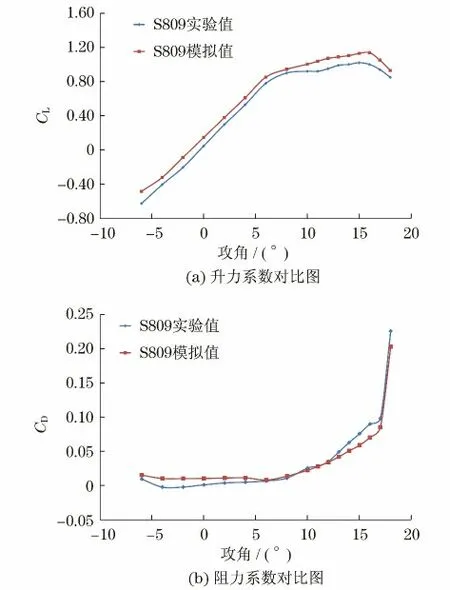
图5 S809实验值与模拟值的对比Fig.5 Comparison of experiment and simulation result of S809

图5（a）为Re＝7.5×105情况下的OSU 风洞测试静态S809翼型升力系数.从图5（a）中可以看出，最大的升力系数在约16°攻角处获得，数值为1.02.当攻角处于－6°～11°时，模拟的升力系数比实验值大4.2%；而当攻角在11°～18°时，计算得出的CL误差值增至9%.

从图5（b）可以得到，实验值阻力系数在较大的攻角范围内均保持在较低的状态.当攻角处于－6°～16°时，模拟的阻力系数与实验值的误差均保持在8%以内，当攻角处于16°～18°时，误差值达到10%.

由于网格对CFD（computational fluid dynamics）计算结果也有着至关重要的影响，故作者对网格数量作了验证，分别试用了网格数为34 520的非结构性网格和网格数为38 580的结构性网格对S809原始翼型进行模拟，计算结果与实验值的平均误差超过10%，即证明了50 000以下不同数量的网格对计算结果有着不可忽视的影响.但是，一旦网格数超过50 000，继续对网格进行加密，无论增加多少网格，对计算结果没有太大的影响.另外，考虑计算经济性以及时间成本的情况下，50 000的网格数即满足计算要求.

此外，在CFD计算中使用了壁面函数，因为，在壁面周围的压力梯度很大，需要排除在边界层中存在解析解的情况，并检查了一次层网格质心到壁面的无量纲距离y＋.从图6 可以看出，y＋的范围较小，第一层网格布置得比较合理.因此，采用上述网格数量及质量可以得到较为准确的模拟结果.

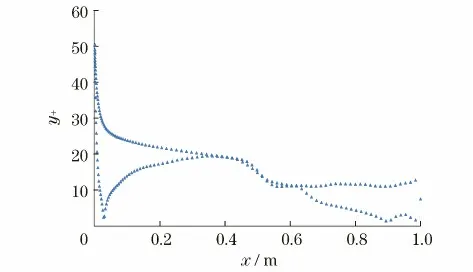
图6 壁面附近（S809原始翼型）Fig.6 y＋near the airfoil（original S809airfoil）

综上所述，升阻力系数的模拟结果与试验值曲线吻合得比较好，虽然存在一定误差，但是，研究重点是不同尾缘摆角对翼型气动性能的影响，属于比较性研究，稍有偏差并不影响最终结论.所以，采用的算法是可靠的.

2.3 尾缘摆角对翼型升阻力系数的影响

图7为S809原始翼型及上摆－5°、下摆5°、下摆10°、下摆15°后翼型在不同攻角下的静态CL和CD.

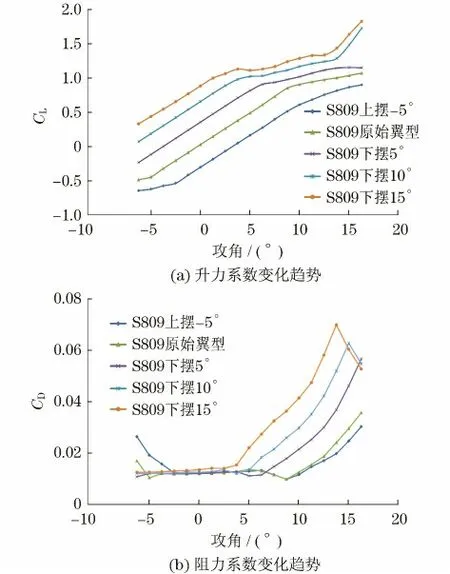
图7 尾缘摆动后静态升阻力系数随攻角的变化关系Fig.7 Variation trend of lift and drag coefficient of deformed airfoils with the change of angle of attack

由图7（a）可知，在－6°～12°攻角范围内，下摆翼型的CL整体上较原始翼型高.表2 为摆角翼型相对于S809原始翼型升力系数提高的平均值.

表2 摆角翼型相对于S809原始翼型升力系数提高的平均值Tab.2 Comparison of the average value of the increasing CLof deformed airfoils with that of original S809airfoil

原始翼型的升力系数在小攻角范围内，会随着攻角的变大而保持变大趋势，其中，对于下摆5°，10°，15°这3条升力曲线，当攻角在－5°～4°区间为线性区域（翼型表面为完全附着流动），而攻角在4°～12°区间则为非线性区域（翼型表面为转捩流动或部分分离流动）.

原始翼型在－6°～16°攻角范围，升力系数变化范围为－0.48～1.14，而下摆翼型当攻角范围为－6°～4°时，升力系数变化范围可完全满足原始翼型运行于－6°～16°攻角范围时的升力系数变化范围，且在整个区间内与攻角均保持线性关系（翼型表面为完全附着流动）.

当翼型处于5°～20°攻角范围内，虽然曲线呈现非线性特征，但是，升力系数仍随着攻角的增大而增大.

由图7（b）可知，对于原始翼型，当攻角为－6°～12°时，最大与最小阻力系数变化区间为0.013 08～0.035 68；而对于尾缘摆动后的翼型，攻角仅为－5°～4°时，最大与最小阻力系变化范围就可以达到0.011 12～0.027 37，即在同样升力系数区间内，尾缘下摆后翼型的阻力系数比原始翼型的阻力系数更小.

2.4 变形翼型表面静压分布

如图8所示，随着尾缘下摆角度的增加，翼型下表面压力也随之增大，并且在前缘点和尾缘点位置压力梯度特别大.从压差的量级上来看，上摆－5°翼型上下表面压差最小（图8（a）），下摆15°翼型压差最大（图8（e）），从而可以更清楚地证明了尾缘摆角可以提高升阻比.

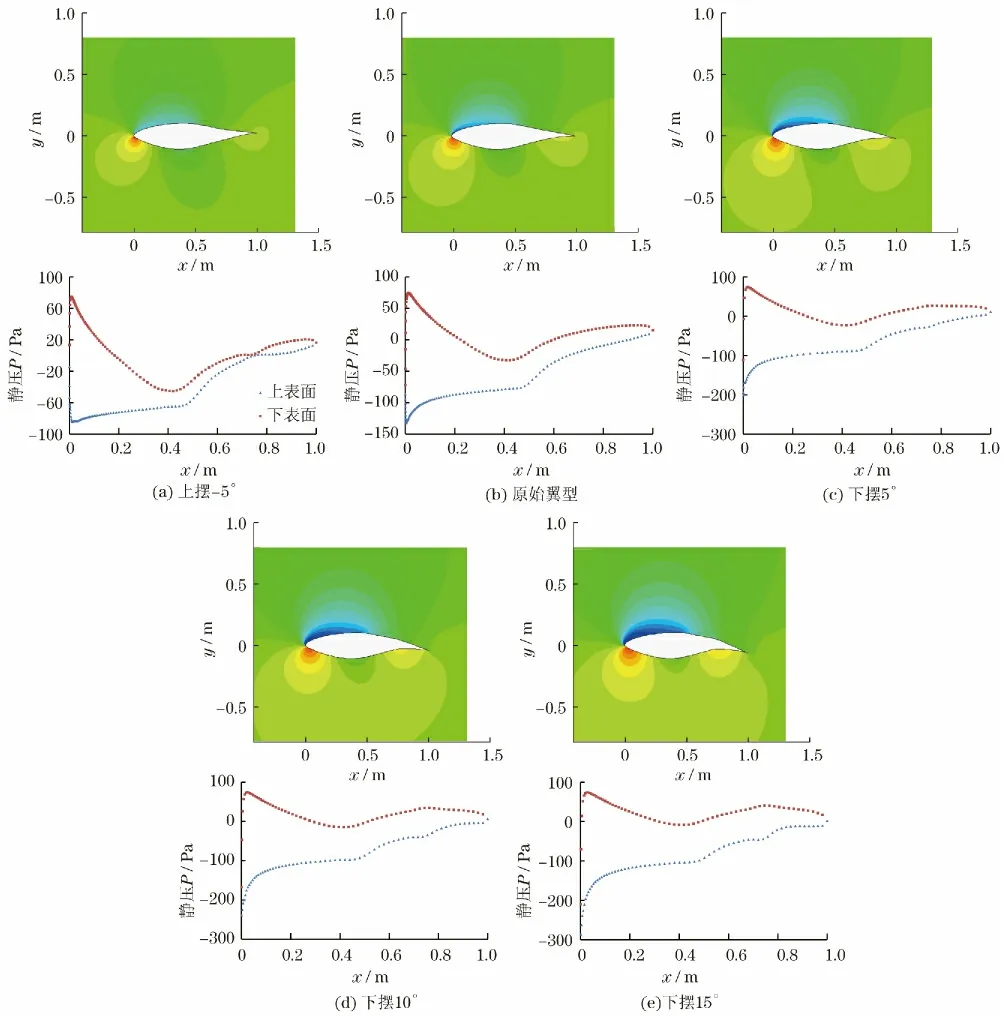
图8 变形翼型表面静压分布Fig.8 Static pressure distribution on the deformed airfoil surface

2.5 尾缘摆角对翼型流动分离特性的影响

尾缘下摆对翼型升阻力系数起到了较好的改善，但是，尾缘摆动对翼型流线存在不利的影响，如图9所示.由图9（a）和图9（b）中可以看出，尾缘上摆－5°和原始翼型在8°攻角下并没有产生旋涡，而下摆翼型出现了旋涡，对应到升阻力系数图（图7）上，可以看到8°攻角处上摆翼型的升阻力系数明显发生了突变.

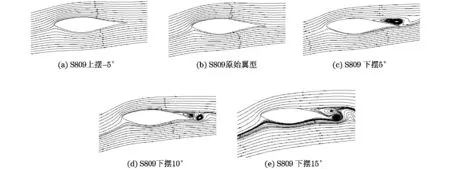
图9 翼型流线图（8°攻角）Fig.9 Streamline of airfoil（angle of attack is 8°）

下摆5°时（图9（c））开始出现较小的旋涡，并且旋涡在翼型尾部刚产生；下摆10°时（图9（d）），旋涡变大，并且开始向翼型前缘处蔓延，并可以看出旋涡呈脱落状；到下摆15°时（图9（e）），明显可以看到有一对旋转方向相反的旋涡存在.从图9（a）—9（e）的变化趋势可以看出，随着尾缘下摆角度的增加，翼型尾缘部分出现流线分离的攻角明显变小.一旦翼型尾缘出现流线分离后，由于湍流模型等因素，模拟值的误差会增大.

上摆－5°翼型相对于原始翼型，CL平均减小约17.6%，CD变化较小.另据计算，原始翼型于16°攻角开始产生流线分离现象，而上摆－5°翼型在攻角14°时即开始发生流线分离.

综上所述，原始S809 翼型高升阻比区间为－6°～16°区间，随着S809尾缘下摆5°，10°和15°，翼型的升阻力系数较原始翼型的有较大的改善，而且最大升阻比明显变大.然而，由于尾缘摆动，改变了原始翼型的流动性能，翼型随着下摆角度的增大，翼型产生分离涡的攻角却随之提前，翼型完全附着流动攻角区间减小到－5°～4°，正常运行区间大幅减小，更容易形成失速.对于上摆－5°翼型，其升阻比较原始翼型的差，翼型完全附着流动攻角区间为－3°～14°，总体而言气动特性较原始翼型的差.

3 结 论

对S809翼型的尾缘部分进行适当变形，利用CFD软件对S809上摆－5°、下摆5°，10°及15°变形翼型作了数值模拟，分析了各个翼型的特点，针对翼型的升阻力系数、上下表面压力、失速等方面，研究了攻角与摆角对翼型气动特性的影响，并总结了相关规律.

a.在小攻角工况下，尾缘摆角较大的翼型相对于摆角较小的翼型升力系数更高，而阻力系数基本不变，故升阻比得到了较好的提高，升力系数的最大值变大，大升阻比攻角范围比原始翼型的更宽.

b.对于变形翼型，随着翼型尾缘摆角的增大，其尾缘部分的流动就越容易出现分离，而且，当攻角超过4°，分离涡向翼型前缘蔓延的趋势就越明显，会导致较多的损失，最终引起阻力系数的增大.

c.随着尾缘下摆角度变大，翼型上下表面压差也随之明显变大.翼型下表面压力增大，上表面压力逐渐减小，并且在前缘点与尾缘点位置压力梯度特别大.上摆－5°时翼型上下表面压差最小，下摆15°时翼型上下表面压差最大.

d.上摆翼型升阻力特性及失速特性均较原始翼型的差，故上摆翼型的气动性能不如S809原始翼型的.

［1］李春，叶舟，高伟，等.现代陆海风力机计算与仿真［M］.上海：上海科学技术出版社，2012.

［2］The Danish Society of Engineers and the Federation of Engineers.DS 472Loads and safety of wind turbine construction［S］.Copenhagen：Dansk Standard，1992.

［3］Kooijman H J T，Lindenburg C，Winkelaar D，et al.DOWEC 6MW pre－design：aero－elastic modeling of the DOWEC 6 MW pre－design in PHATAS［R］.Petten：Energy Research Center of the Netherlands，2003.

［4］Sharma R N，Madawala U K.The concept of a smart wind turbine system［J］.Renewable Energy，2012，39（1）：403–410.

［5］Pasupulati S V，Wallace J，Dawson M.Variable length blades wind turbine［C］∥Power Engineering Society General Meeting，IEEE，2005，3：2097－2100.

［6］Barlas T K，Van Kuik G A M.Review of state of the art in smart rotor control research for wind turbines［J］.Progress in Aerospace Sciences，2010，46（1）：1－27.

［7］Mohamed M H，Wetzel K K.3D woven carbon／glass hybrid spar cap for wind turbine rotor blade［J］.Journal of Solar Energy Engineering，2006，128（4）：562－573.

［8］Rajadurai J S，Christopher T，Thanigaiyarasu G，et al.Finite element analysis with an improved failure criterion for composite wind turbine blades［J］.Forschung im Ingenieurwesen，2008，72（4）：193－207.

［9］张建，陈榴，戴韧，等.下游塔架对水平轴风力机叶片气动负荷的作用［J］.上海理工大学学报，2010，32（1）：73－78.

［10］Andrew T L，Richard G J.Compliant blades for wind turbines［J］.IPENZ Transactions，1999，26（1）：7－12.

［11］Veers P S，Eisler G R，Laino D J，et al.The use of twist－coupled blades to enhance the performance of horizontal axis wind turbines［R］.New Mexico：Sandia National Laboratories，2001.

［12］Maheri A，Noroozi S，Toomer C A，et al.WTAB，a computer program for predicting the performance of horizontal axis wind turbines with adaptive blades［J］.Renewable Energy，2006，31（11）：1673－1685.

［13］Maheri A，Noroozi S，Vinney J.Application of combined analytical／FEA coupled aero－structure simulation in design of wind turbine adaptive blades［J］.Renewable Energy，2007，32（12）：2011－2018.

［14］Maheri A，Isikveren A T.Design of wind turbine passive smart blades［C］∥European Wind Energy Conference.2009.

［15］NREL’s S809 Airfoil graphic and coordinates［EB／OL］.NREL.（2009－10－21）［2013－4－20］.http：∥wind.nrel.gov／airfoils／Shapes／S809－Shape.html.

［16］Ramsay R R，Hoffman M J，Gregore K G.Effects of grit roughness and pitch oscillations on the S809airfoil［R］.Golden，Colorado：National Renewable Energy Laboratory，1995.