非线性优化问题的光滑化序列二次规划方法

宇振盛， 张丽娜， 秦 毅

（上海理工大学 理学院，上海 200093）

1 问题的提出

考虑非线性优化问题

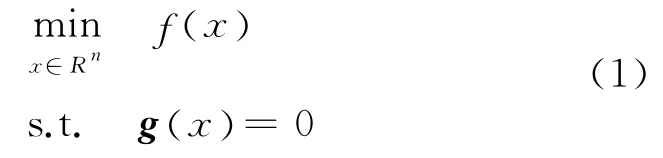
其中，x∈Rn，f：Rn→R，g：Rn→Rm是连续可微函数.

此类问题广泛应用于随机规划、最优控制以及半无限规划和原始分解算法中［1－3］，在过去的几十年里，人们已经提出了许多数值方法来解决这一问题.其 中，序 列 二 次 规 划 法（sequential quadratic programming，SQP）是使用最广泛的方法之一，这类算法具有良好的全局收敛性，得到最优解时需要的迭代次数也较少.该方法由Wilson［4］最早针对凸优化问题提出，并由Biggs［5］，Han［6］和Powell［7－8］等推广到一般问题，有关综述报告可参见文献［9］.

由与问题（1）相关的SQP 理论可知，可以通过迭代公式

来产生出收敛到问题（1）的Karush－Kuhn－Tucker（KKT）点的点列.其中，λk是由某些线搜索方法获得的，用来降低评价函数的函数值的步长，dk是二次规划问题

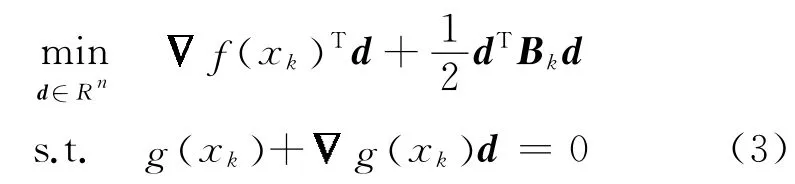
的解.Bk是目标函数的拉格朗日函数的近似Hessen矩阵，通常由拟牛顿法获得.

在SQP理论中，最常使用的评价函数是不可微精确罚函数

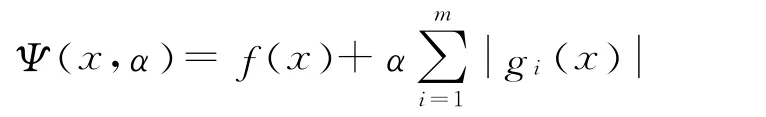
因为函数Ψ （x ，α） 的不可微性，从而给计算带来一定的困难.为克服此困难，通常可用光滑的罚函数作为其评价函数［10］.本文使用逼近光滑罚函数［10－11］

来作为SQP算法的评价函数.其中，Φ（x，α，μ）是逼近于Ψ （x ，α） 的，并且是连续可微的.文献［11］中的数值试验显示，该光滑罚函数的性态良好.

2 光滑化SQP算法

使用逼近光滑罚函数

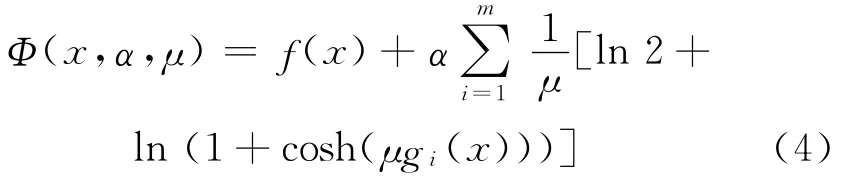
作为SQP算法的评价函数.首先给出函数Φ（x，α，μ）的性质.

引理1 函数Φ（x，α，μ）的性质［11］

a.对任意固定的μ，若f（x ） ，gi（x ）是k 阶连续可微的，i＝1，2，…，m，则Φ（x，α，μ）也是k 阶连续可微的.若f（x ），gi（x ）是 两 阶 连 续 可 微 的，则有

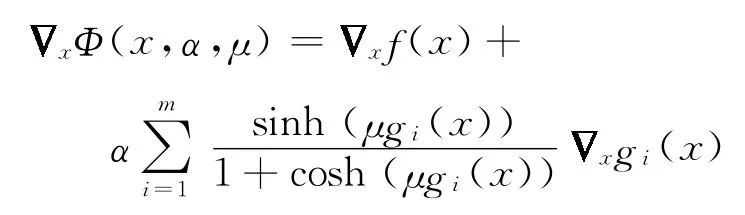
和

b.若f（x ） ，gi（x ）是凸的，i＝1，2，…，m，则Φ（x，α，μ）也是凸的.

c.Φ（x，α，μ）＞Ψ（x，α），∀x∈Rn.

f.若μ1＜μ2，则Φ（x，α，μ1）＞Φ（x，α，μ2），∀x∈Rn.

现在考虑SQP算法的迭代公式

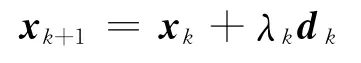
其中，dk是下列二次子问题的解

式中，Bk是n×n 对称正定矩阵.

本文中总是假定子问题（5）是可行的.在这种假设下，如果Bk是正定矩阵，那么，子问题（5）有唯一解dk，并且dk是子问题（5）的解当且仅当存在拉格朗日乘数ρk使得KTT条件成立

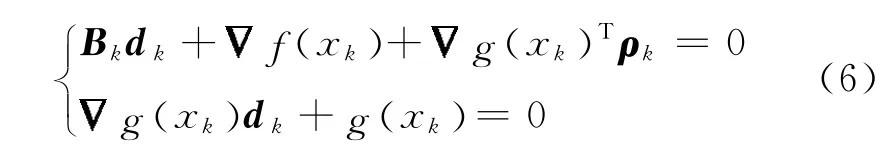
引理2［12］假设Bk是对称正定矩阵，则点对是问题（1）的KTT点对当且仅当，）是子问题（5）的KTT点对.

下面叙述基于光滑化罚函数（4）的SQP算法.

算法1

步骤0 给定x1∈Rn，ρ1∈Rm，β∈（0，1），γ∈（0，1），ε≥0，B1∈Rn×n为 对 称 正 定 矩 阵，μ0＞1，α0＞1，M ＞1，令k：＝1.

步骤1 求解子问题（6），得到dk和.若，则算法终止.

步骤3 若

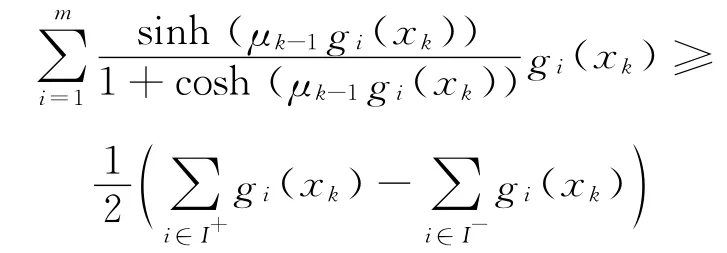
其中

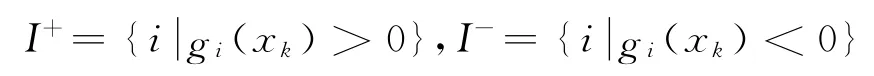
则令μk：＝μk－1，转步骤5；否则，转步骤4.

步骤4 令μk－1：＝Mμk－1，转步骤3.

步骤5 若

则令αk：＝αk－1，转步骤7；否则，转步骤6.

步骤6 令αk－1：＝Mαk－1，转步骤5.

步骤7 令λk为序列｛1，γ，γ2，… ｝中使下列不等式成立的最大值：

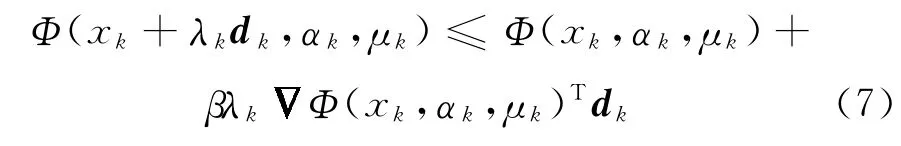
步 骤8 令xk＋1＝xk＋λkdk，ρk＋1＝ρk－，通 过BFGS 校 正 公 式 将Bk修 正 为Bk＋1，令k：＝k＋1，转步骤1.

算法1中提到的BFGS校正公式如下［12］：

正.令

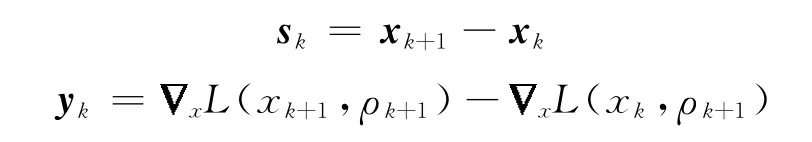
令

式中，参数θk定义为

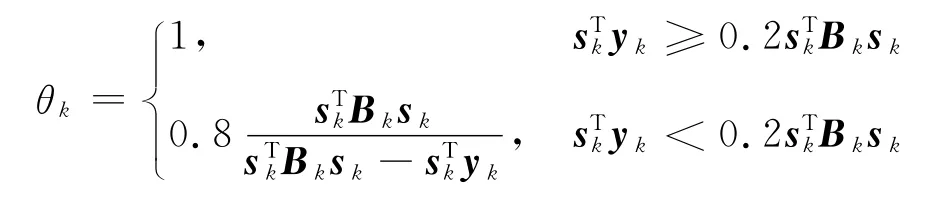
于是，矩阵Bk的BFGS校正公式为

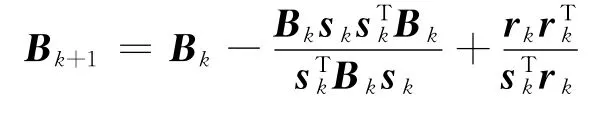
3 算法的全局收敛性

在分析算法1的全局收敛性之前，假设以下的条件成立.

假设A：

首先分析算法1的可行性.

引理3 算法1不会在步骤3和步骤4之间无限循环.

证明

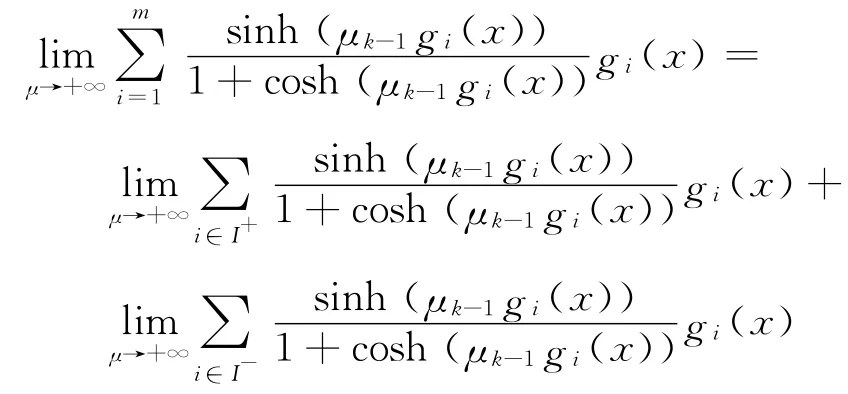
因为

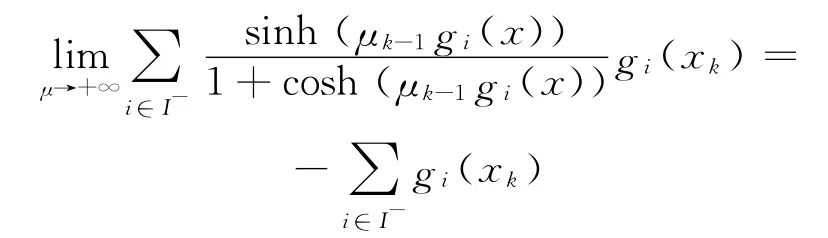
和

引理3得证.

引理4 算法1不会在步骤5和步骤6之间无限循环.

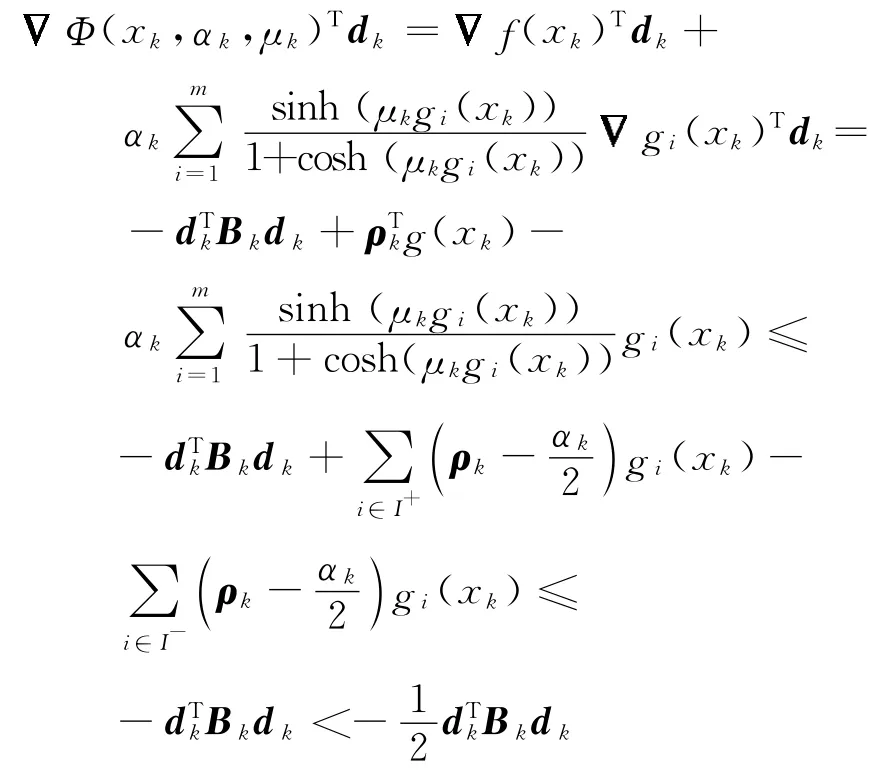
引理4得证.

引理5 当算法1到达步骤7时，有

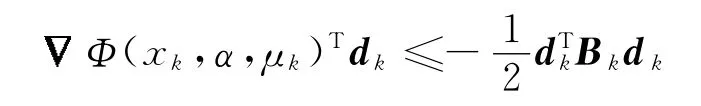
引理5的成立是显然的.

定理1 由算法1所产生的序列x｛ ｝k 的任一聚点均为问题（1）的KTT点.

证明 首先，证明

从算法1中可以得知，μ｛ ｝k 是单调非减序列.又由引理1和步骤7，可以知道

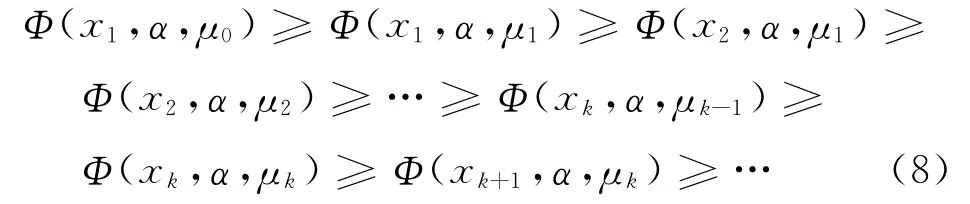
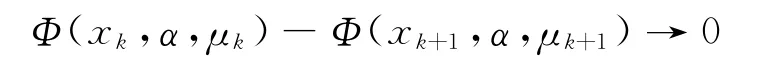
由式（8），Φ（xk，α，μk）－Φ（xk＋1，α，μk）→0.

又由步骤7可知

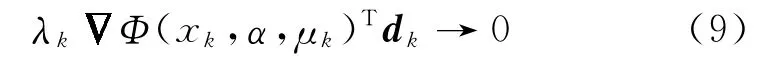
现证明λk→0不成立.反证，若λk→0，从算法1中可以得知，有

另一方面，

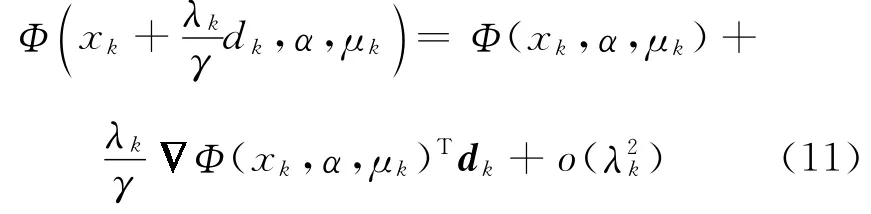
由式（10）和式（11），有

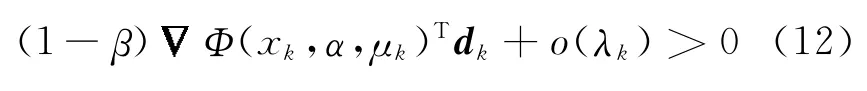
然而，由引理5，有

于是，导出矛盾.

由式（9）和λk→0不成立，有

又由式（13），假设A 的b和式（14），可以得到dk→0.

由文献［13］中的定理3.2.1、定理4.3.3和本文中的引理3，可知定理1的结论成立

4 数值测试

在一台CPU 1.70GHz，RAM 512MB 的PC 上利用Mathematica 7.0.1编程实现了算法1.测试函数取自文献［14－16］，计算结果如表1所示，其中，HS（i）表示文献［14］中的第i个算例，S（i）表示文献［15］中的第i个算例.在算法中，各参数分别取为β＝0.5，γ＝0.5，M ＝2，μ0＝2，α0＝2，ρ1＝0m×1，B1＝In，ε＝10－6.表1的算例说明，对于测试的问题，本文的算法在很短的时间和较少的迭代次数内可求得问题较为满意的解.

表1 数值测试结果Fig.1 Numerical test results

5 结束语

结合一类双曲余弦型光滑化罚函数，给出了求解等式约束优化问题的SQP算法，获得了算法的全局收敛性，并验证了算法的有效性.对于该类函数如何结合一般的非光滑问题［17］及其它有效算法，如信赖域算法［18］，值得进一步研究.

［1］Qi L Q.Superlinearly convergent approximate Newton methods for LC1optimization problems［J］.Mathematical Programming，1994，64（1／2／3）：277－294.

［2］Rockafellar R T.Computational for large－scale problems in extended linear－quadratic programming［J］.Mathematical Programming，1990，48（1／2／3）：447－474.

［3］Rockafellar R T，Wets R J B.Generalized linearquadratic problems of deterministic and stochastic optimal control in discrete time［J］.SIAM Journal on Control and Optimization，1990，28（4）：810－922.

［4］Wilson R B.A simplicial method for convex programming［D］.Boston：Harvard University，1963.

［5］Biggs M S.Constrained minimization using recursive equality quadratic programming in numerical methods for nonlinear optimization［M］∥Lootsma F A，ed.Numerical Methods for Nonlinear Optimization.London，New York：Academic Press，1972：411－428.

［6］Han S P.A globally convergent method for nonlinear programming［J］.Journal of Optimization Theory and Applications，1977，22（3）：297－309.

［7］Powell M J D.A fast algorithm for nonlinearly constrained optimization calculations.Lecture Notes in Mathematics［M］∥Waston G A.Lecture Notes in Mathematics.Berlin：Springer Verlag，1978，630：144－157.

［8］Powell M J D.The convergence of variable metric methods for nonlinearly constrained optimization calculations［M］∥Nonlinear Programming.New York：Academic Press，1978：27－63.

［9］Gould N I M，Toint P L.SQP methods for large－scale nonlinear programming［C］∥IFIP—the International Federation for Information Processing，2000，46：149－178.

［10］Zhang J L，Zhang X S.An SQP method based on smoothing penalty function for nonlinear optimizations with inequality constraint［J］.Journal of Systems Science and Complexity，2001，14（2）：212－217.

［11］Herty M，Klar A，Singh A K，et al.Smoothed penalty algorithms for optimization of nonlinear models［J］.Computation Optimization and Application，2007，37（2）：157－176.

［12］黄红选，韩继业.数学规划［M］.北京：清华大学出版社，2006.

［13］Bank B，Guddatt J，Klatle D，et al.Nonlinear parametric optimization.Birkhäuesr［M］.Berlin：Akademie－Verlag，1982.

［14］Hock W，Schittkowski K.Test examples for nonlinear programming codes［M］∥Lecture Notes in Economics and Mathematical Systems.Berlin：Springer－Verlag，1981，187.

［15］Schittkowski K.More test examples for nonlinear programming codes［M］∥Lecture Notes in Economics and Mathematical Systems.Berlin：Springer－Verlag，1981，282.

［16］Andrei N.An unconstrained optimization test functions collection［J］.Advanced Modeling and Optimization，2008，10（1）：147－161

［17］刘晶，高岩.求解一类无限维非光滑算子方程的光滑化牛 顿 法［J］.上 海 理 工 大 学 学 报，2008，30（2）：167－170.

［18］王安琪，宇振盛，曹倩倩.线性约束优化的一个自适应非单调信赖域算法［J］.上海理工大学学报，2010，32（6）：545－548.