广义测不准关系对电子自旋极化输运性质的影响＊

王伦舟，龙超云，隆正文

(贵州大学 理学院，贵州 贵阳 550025)

磁性隧道结中与电子自旋极化相关的量子输运是自旋电子学的前沿研究领域之一。1977 年，Julliere 提出了Julliere 模型，用于揭示实验上观测的磁性隧道结中隧穿电导的相对变化规律［1］。1989 年，Slonczewski 提出自由电子的Slonczewski模型，进一步考虑了势垒高度对隧穿磁阻的影响［2］。基于Julliere 模型和Slonczewski 模型，近年来，人们对于各种结构的磁性隧道结中自旋极化的输运性质做了广泛和深入的研究，并且得到了不少有意义的成果［3-9］。但这些研究都是基于通常量子理论的，其理论预言与实验结果并非完全一致，有的只能定性解释实验结果，有的仅为理论预言。因此，从不同的侧面对介观磁结构的输运规律进行探索和研究是有必要的。

近些年来，量子理论的相关研究表明，通常量子理论仅仅是广义测不准关系框架下的量子理论的特殊情况。广义测不准关系，又称为广义不确定性原理(Generalized Uncertainty Principle)，是在量子引力相关理论的研究时提出来的，其核心在于描述了一个“最小可观测长度”的存在，这为理论物理的相关研究开辟了一个很有意思的研究方向。目前国内外物理学界在这方面的相关研究很多，也取得了不少理论和实验的研究成果［10-15］。

我们知道，海森堡不确定原理指出一个微观粒子的某组物理量(如位置和动量等)不可能同时具有确定的数值，其中一个量越确定，另一个量的不确定程度就越大。在海森堡不确定性原理中，并不存在最小的可观测长度，也就是说，最小长度可以无限趋近于0。

但是在当前物理学界主流的量子引力理论如超弦理论、圈量子引力理论等，都提出了一个基本观点，即存在一个普朗克尺度大小的最小可观测长度，约为10-35m。这与海森堡不确定性原理完全不同。考虑到这个基本尺度即最小可观测长度的存在，我们需要修正海森堡不确定性原理为所谓的广义不确定性原理。

所以，本文从广义测不准关系出发，进一步研究FM/FI/FM 磁性隧道结中电子自旋极化输运性质，这对于进一步揭示电子输运规律和指导自旋量子器件设计具有积极意义，同时也为广义测不准关系下新量子理论的正确性提供可供实验检验的途径，有助于推动对广义测不准关系下量子理论的深入研究。

1 广义测不准关系

在海森堡不确定性原理中，坐标算符与动量算符满足

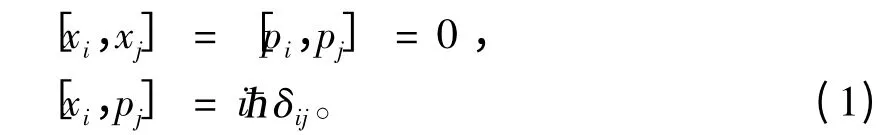
位置与动量的不确定关系为

而在广义测不准关系中，坐标算符与动量算符的对易关系如下［10，11］

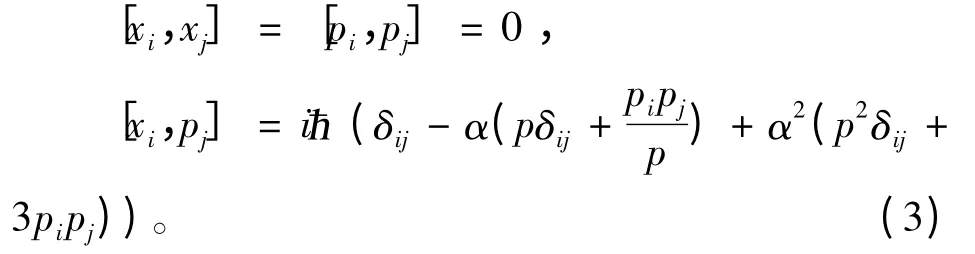
而位置与动量的不确定关系则表示为

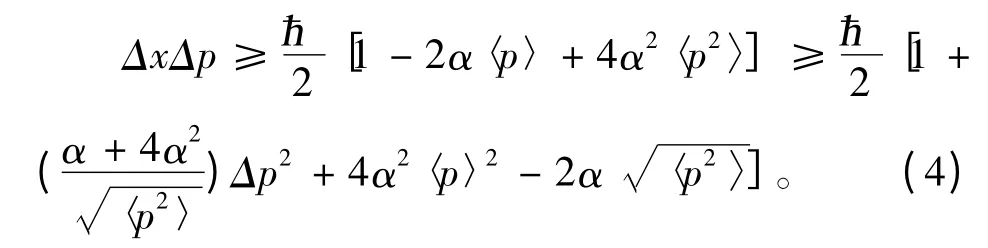
显而易见，当α=0 时，广义测不准关系便会退化成海森堡不确定关系。

在对广义测不准关系下的相关量子问题进行具体研究时，可以定义广义测不准关系下的坐标和动量算符满足:

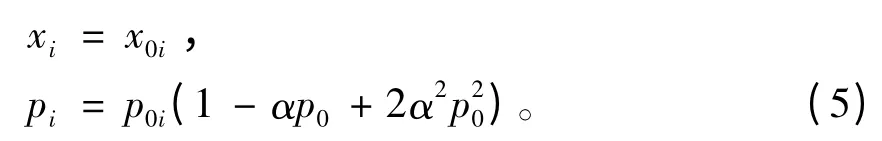
其中x0i，p0j满足对易关系［x0i，p0j］=iħ δij。可以验证，上述算符定义是符合广义测不准关系下量算符的对易关系(3)的。

显然，由于坐标和动量算符的改变，同一量子系统的哈密顿量在通常量子理论和在广义不确定关系下的量子理论中的形式也会完全不同，这也使得广义测不准关系下的量子理论常常表现出与通常量子理论不同的性质。

2 理论模型和相关计算

研究电子沿x 方向在如图1 所示的铁磁体/绝缘体/铁磁体(FM/FI/FM)隧道结的自旋极化输运性质。该结构分为3 个区域，中间方势垒层的厚度为d，两侧铁磁层厚度在理论处理中可视为无限厚。

通常量子理论下，利用Slonczewski 自由电子模型，沿x 方向的哈密顿算符可以表示如下

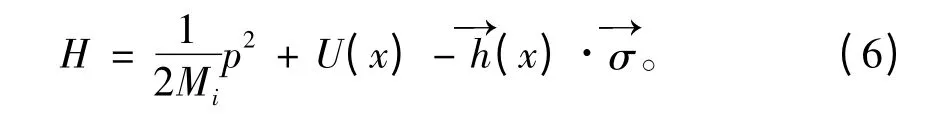
将算符变换(5)代入上式，可得到广义测不准关系下的哈密顿算符如下

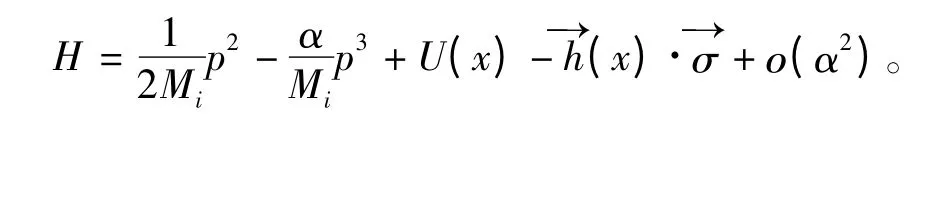
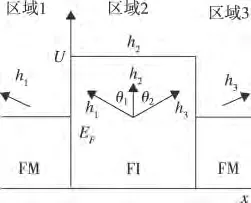
图1 FM/FI/FM 磁性隧道结示意图

式中Mi(i=1，2，3)为隧道结各个区域电子的有效质量;U(x)为与自旋无关的势能，当0 ＜x ＜d 时，U(x)=U0，在其他区域时U=0 。代表s-d 交换作用

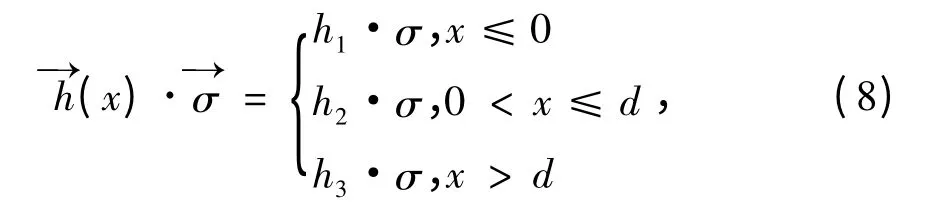
hj(j=1，2，3)为分子场，| h1|=| h3|=h0，| h2|=h0，设h2方向与势垒一致，h1、h3与h2的夹角分别为θ1和θ2，σ为Pauli 自旋算符，σ=±1分别表示自旋↑和↓，即当电子磁矩平行或反平行于分子场时的方向。

设自旋↑的平面波从图1 所示的区域1 左边入射，根据Schrödinger 方程Hψ=Eψ，可以写出区域1、区域2 和区域3 的波函数表达式如下［11］

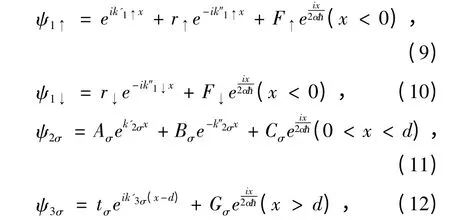
式中，

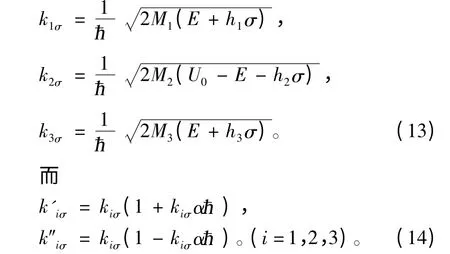
波函数系数Aσ，Bσ，rσ，tσ由函数ψ 及其一阶导数dψ/dx 在边界处连续性条件决定，考虑分子场方向在边界处变化满足的旋量关系

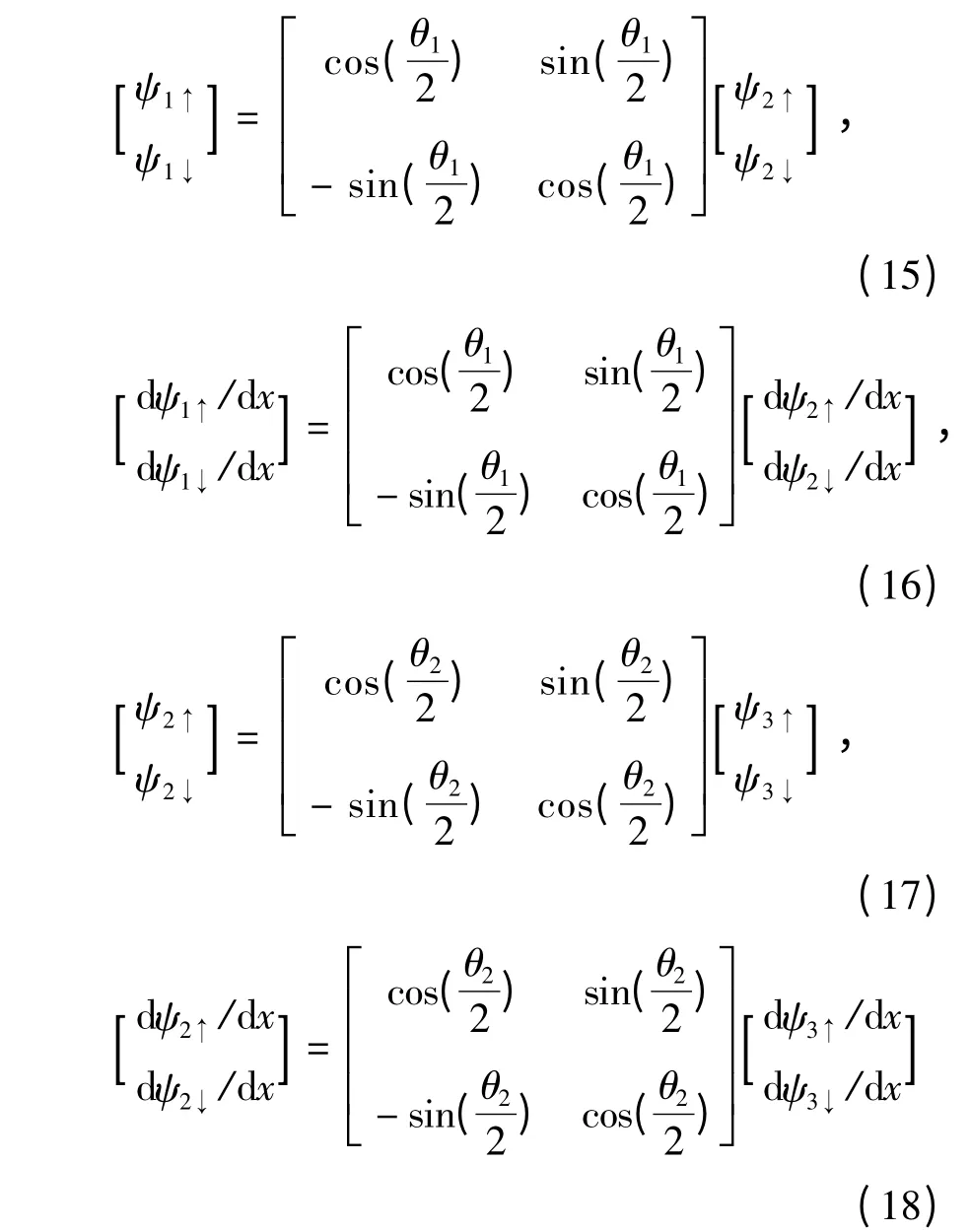
通过上述方程组(15)-(18)可以得到透射系数tσ的解析式。

由几率流密度公式

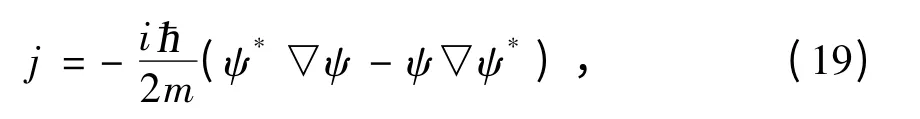
可得电子的透射率

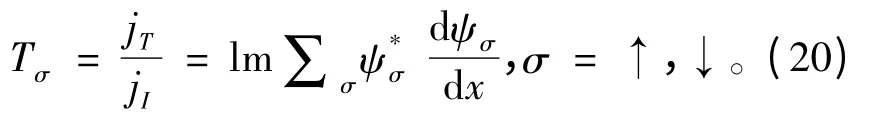
磁性隧道结中自旋σ 的电子隧穿电导

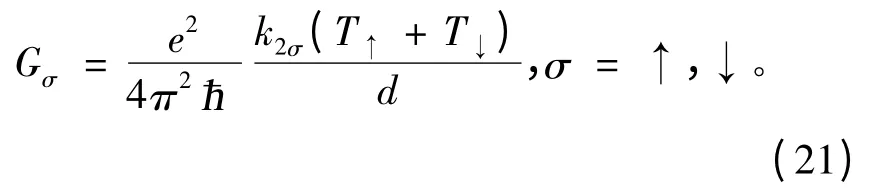
则总的隧穿电导为

3 结果与分析

在计算中，取材料费米能EF=2.6 eV，分子场h0=0.18 eV，h=0.065 eV，方势垒宽d=6.4 nm，势垒高U0=3.0 eV，电子有效质量取为自由电子的质量。对于广义测不准关系相关参数，取α0=1，Cσ≈Fσ≈Gσ～ο(α2ħ2)～10－70［11-13］。可作出广义测不准关系下隧穿电导G 随分子场相对取向θ1和θ2的变化图如图2 所示。而图3 则是通常量子理论下隧穿电导随分子场相对取向的变化图。

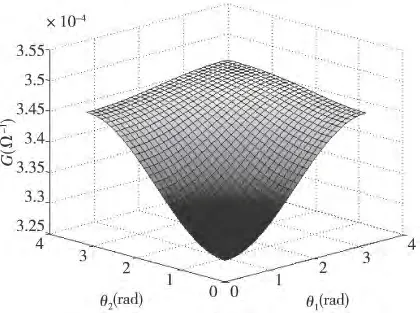
图2 广义测不准关系下隧穿电导随分子场取向的变化

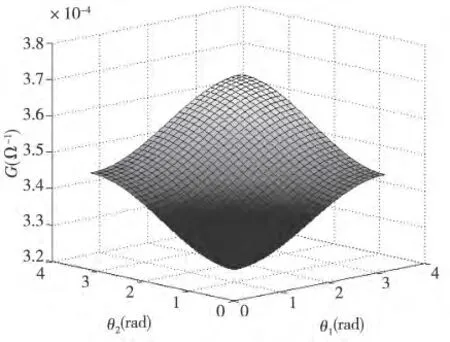
图3 通常量子理论下隧穿电导随分子场取向的变化

磁性隧道结的电子隧穿特性依赖于铁磁层和中间层的分子场的相对取向。由图2 和图3 可见，广义测不准关系下的量子理论和通常量子理论下的隧穿电导极值点是相同的，在θ1=θ2=0 取得最小值，此时两铁磁层的分子场取向平行，且与方势垒的分子场取向相同;而在θ1=θ2=π 时取得最大值，此时隧穿磁阻最小，两铁磁层的分子场取向平行且与方势垒的分子场取向相反。但比较图2 和图3，可以看出广义测不准框架下，隧穿电导的最小值基本一致，而最大值则略小于通常量子理论的结果，这说明隧穿磁阻的最小值是略大于通常量子理论得到的最小值。同时可以看到隧穿电导的变化趋势明显快于通常量子理论下的变化趋势，特别在θ1=0，θ2=π 和θ1=π，θ2=0 处，隧穿电导的值已经非常接近于最大值，说明此时的隧穿磁阻是小于通常量子理论下的计算结果的。

［1］Julliere M.Tunneling between ferromagnetic films［J］.Physics Letters A，1975，54(3):225-226.

［2］Slonczewski J C.Conductance and exchange coupling of two ferromagnets separated by a tunneling barrier［J］.Physical Review B，1989，39(10):6995-7002.

［3］Zhang X D，Li B Z，Sun G，et al.Spin-polarized tunneling and magnetoresistance in ferromagnet/insulator (semiconductor)single and double tunnel junctions subjected to an electric field［J］.Physical Review B，1997，56(9):5484-5488.

［4］Zhang W S，Li B Z，Li Y.Conductance，magnetoresistance，and interlayer exchange coupling in magnetic tunnel junctions with nonmagnetic metallic spacers and finite thick ferromagnetic layers［J］.Physical Review B，1998，58(22):14959-14965.

［5］Zhuravlev M Y，Jaswal S S，Tsymbal E Y，et al.Ferroelectric switch for spin injection［J］.Applied Physics Letters，2005，87(22):222114.

［6］谢征微，李伯臧.处理具有任意形状势垒的磁性隧道结中电子输运的一个简单方法［J］.物理学报，2005，51(2):399-405.

［7］赵俊卿，乔士柱，张宁玉，等.磁性隧道结自旋极化电子的隧穿特性［J］.计算物理，2008，25(2):235-240.

［8］金莲，朱林，李玲，等.多层结构双自旋过滤隧道结中的电子输运特性［J］.物理学报，2009，58(12):8577-8583.

［9］杨军，章曦，苗仁德.自旋场效应晶体管中隧道磁阻的势垒相关反转效应［J］.物理学报，2014，63(21):217202-217202.

［10］Scardigli F.Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment［J］.Physics Letters B，1999，452(1):39-44.

［11］Brau F.Minimal length uncertainty relation and the hydrogen atom［J］.Journal of Physics A:Mathematical and General，1999，32(44):7691-7696.

［12］Chang L N，Minic D，Okamura N，et al.Exact solution of the harmonic oscillator in arbitrary dimensions with minimal length uncertainty relations［J］.Physical Review D，2002，65 (12):125027.

［13］Das S，Vagenas E C.Universality of quantum gravity corrections［J］.Physical Review Letters，2008，101(22):221301.

［14］Ali A F，Das S，Vagenas E C.Discreteness of space from the generalized uncertainty principle［J］.Physics Letters B，2009，678(5):497-499.

［15］Ali A F，Das S，Vagenas E C.Proposal for testing quantum gravity in the lab［J］.Physical Review D，2011，84(4):044013.

［16］Nowak J，Raułuszkiewicz J.Spin dependent electron tunneling between ferromagnetic films［J］.Journal of magnetism and magnetic materials，1992，109(1):79-90.