环形交叉口交织区通行能力的一个新理论模型

尹雨丝，吴 中

（河海大学土木与交通学院，江苏 南京210098）

现代环形交叉口在安全、环保、美观方面较传统环形交叉口、信号控制交叉口有较为突出的优势。为驾驶员提供了更好的通视效果，冲突点较普通交叉口少很多，且由于较低的行驶速度使得事故发生率明显减少。随着社会和经济的发展，机动车保有量增加，城市交通拥挤的问题日益显著，在这种环境下环形交叉口如何保持自身的优势，提高通行能力是一个急需研究的课题。

国外对环形交叉口通行能力计算的简化算法认为，环形交叉口交织区只存在交织行为，忽略了我国的混合交通特性突出、拥挤状况下不同特性的驾驶员对于交通组织方式的漠视（例如：不理解环道优先规则，不遵守慢进快出要求，不主动选择正确车道，强行换道引起交通流自锁）等特点，造成资源的浪费。因此，从这一方面入手，从实测数据出发，将交织理论与串行排队理论相结合，推导出更加适合我国城市环形交叉口的理论模型。

1 我国环形交叉口概况

通过大量的现场调查和深入分析，我国典型常规环形交叉口中的交通流具有以下特点。

1）对于单车道环形交叉口，交织区由于只有一条环道，车辆没有条件换道，所以不存在换道行为，车辆换道只在出入口处进行。

2）对于环流车辆具有优先权的双车道环形交叉口，车辆在进出口处会发生强制换道行为，随着车辆进入交织区的目标车道，交织区上的两股交通流一般处于跟驰状态，如果出现可接受间隙，车辆可能会提前换道或者超车，但不属于强制换道。

3）对于共享优先权的双车道环形交叉口，车辆出现强制换道的行为不仅出现在环形交叉口的出入口。直行或者左转的车辆在进入环形交叉口时可以先进入外环道，等待间隙进入内环道，如果不能实现，车辆会一直沿着外环道行驶直至到达目标出口，在这过程中可能会与离开环形交叉口的车辆进行交织。在内环道即将离开环形交叉口的车辆会伺机换道进入外环道，如果在进出口的地方还没有机会换道进入外环道，车辆此时就会进行强行换道，直接离开环形交叉口。

4）环行车道上的车辆一般不会出现超车行为，故其车头时距符合泊松分布［1］。

2 环形交叉口交织区通行能力的理论模型

环形交叉口交织区通行能力主要受环道交通量、交织区车辆车头时距分布、入口道车辆的临界间隙和随车时距、交织区车道长度等方面的影响［2-3］。

现主要研究符合设计规范的具有2条环形车道、2条出入口车道的4路交叉口的环交路口，同时交通组成为单一的标准小汽车。通过大量的观察和分析总结，得到该环形交叉口交织区理想的运行特征为：环道上有2条车道，环形交叉口有充分多的车辆在入口道上等待进入并通过交织区，环道及入口道可以容纳无限多的车辆排队。

该模型以串行排队理论［4］嵌入在环形交叉口交织区强行换道过程中为特征，假设环形交叉口无交通信号；环行车道上车辆无超车行为；环行车辆的车头时距服从泊松分布；车辆换道时间服从独立同分布［5］。

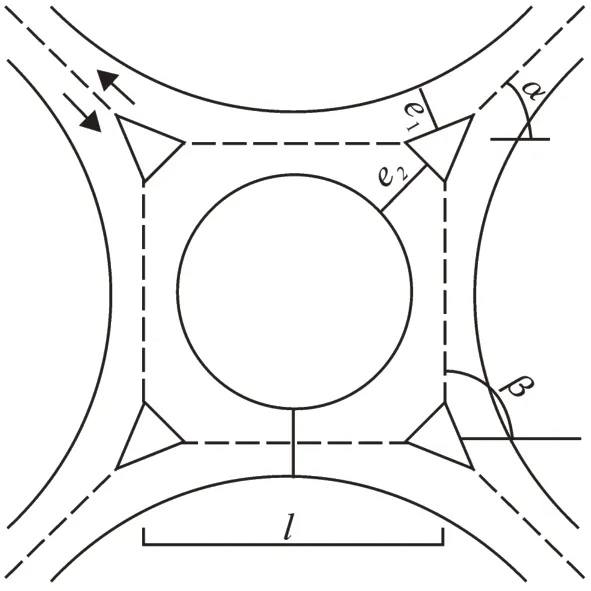
图1 环形交叉口示意图Fig.1 Schematic diagram of roundabout

2.1 模型建立

2.1.1 交织理论计算方法

交织理论认为环形交叉口的车辆运行是通过环道（交织区）上的交织行为来完成的，环形交叉口通行能力通过交叉口交织区的最大通行流量Q1来描述。交织理论模型的代表形式是沃尔卓普（Wardrop）公式：

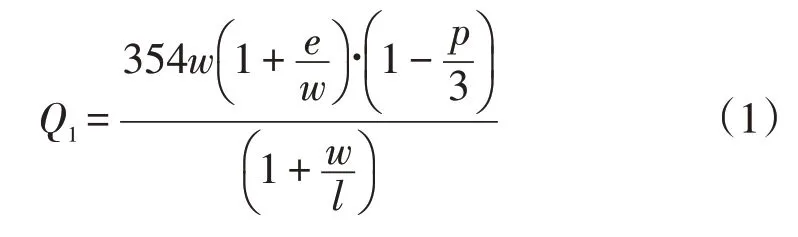
其中：l是交织区长度，m；w是交织区宽度，m；e是环形交叉口入口引道平均宽度，m；p是交织区内进行交织的车辆与全部车辆之比，%。公式相关符号的图示见图1。

2.1.2 基于串行排队理论的计算方法将环道交织区没有车辆强行换道瞬间定义为一个再生点，两个连续的再生点之间的时间间隔为一个周期，周期内车辆平均换道数用c表示。令

式中：T(c)为车辆的换道时间；{} 为周期内第j辆车的换道时间。所有{} 都是服从累积分布函数Fs(t)的独立同分布随机变量。令FT(c)(t)为T(c)的累积分布函数，E[T(c)]为车辆换道时间的期望值，Fs(t)为车辆换道时间的累积分布函数。则

由恒等式

得

4路环形交叉口共4段交织区，取其中一段研究，假设车辆换道时间服从独立同分布，环形交叉口交织区强行换道行为的结果与车辆换道的时间累积分布函数Fs(t)有关［6］，鉴于上述情况，环形交叉口交织区通行能力Q2公式为

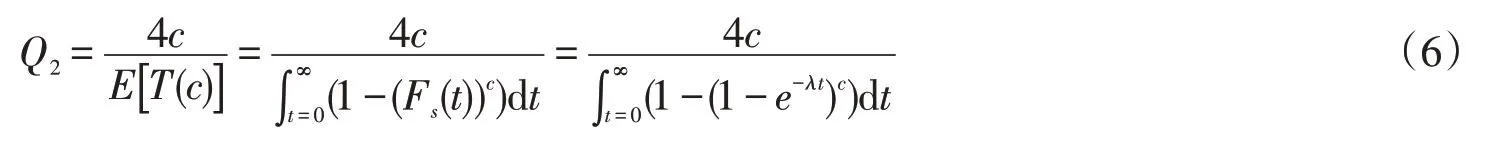
式中：λ=q3600；q为环道车流量。

2.1.3 理论模型

在高峰小时交通量调查的基础上，获得高峰各交织区的高峰小时交通量，及交织区交织车辆和强行换道车辆交通量比例。则环形交叉口交织区通行能力Q公式可以由Wardrop公式与串行排队理论公式结合构造得

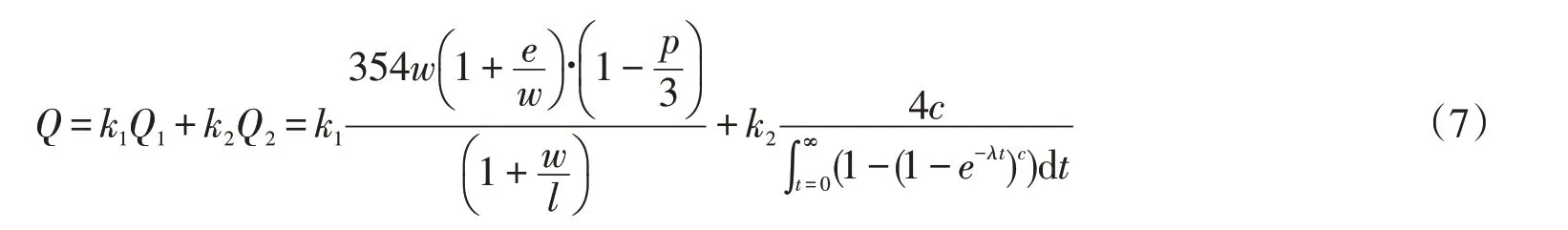
式中：k1为交织区交织车辆占总交通量的比例；k2为交织区强行换道车辆占总交通量的比例。根据大量实测数据统计，k1，k2分别取值为30%和70%［7］。

2.2 模型的验证

为验证模型的准确性，借助VISSIM软件仿真，对实际环形交叉口的交通运行特性进行统计和分析，假设左转和右转车流各占总交通量的25%，直行车流占总交通量的50%，建立了5种中心岛半径的交叉口仿真模型［8］。由于仿真的随机性，为确保仿真结果稳定性，需将仿真初始阶段采集的交通数据剔除，所以每次仿真时间为3 600 s，取600 s以后的数据进行统计分析。软件运行图如图2所示，各进口道流量输入相同，如表1所示。

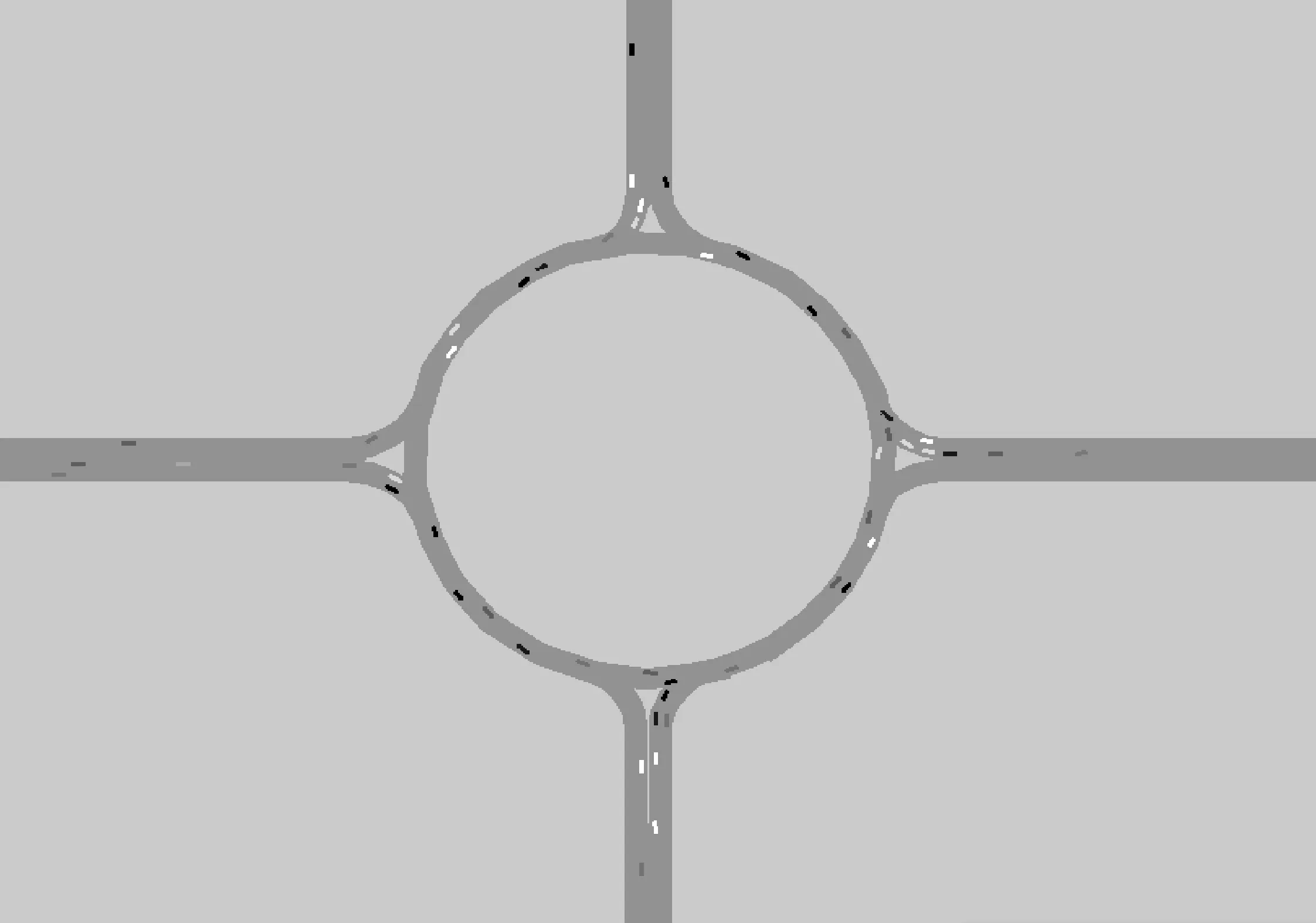
图2 环形交叉口仿真示意图Fig.2 The simulation diagram of roundabout

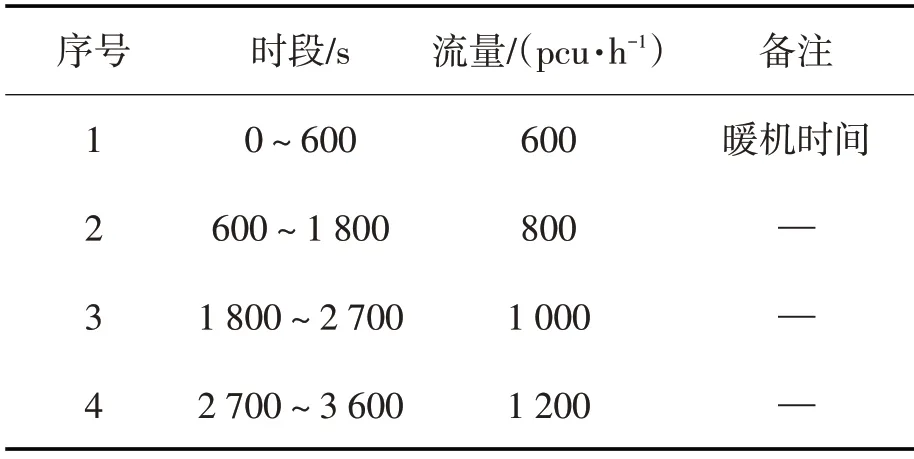
表1 交通流量输入Tab.1 The traffic input

将模型预测结果与仿真结果相比，表2记录了理论结果和仿真结果。

表2 理论模型验证Tab.2 The theroy verification of the model

根据2014年5月18：00—19：00对宁海路广场环形交叉口、枯柳树环形交叉口、石厂环形交叉口、葡萄嘴环形交叉口、鼓楼环形交叉口的流量调查［9］，通过统计分析可得到实测环行流量值与理论值相较如表3所示。

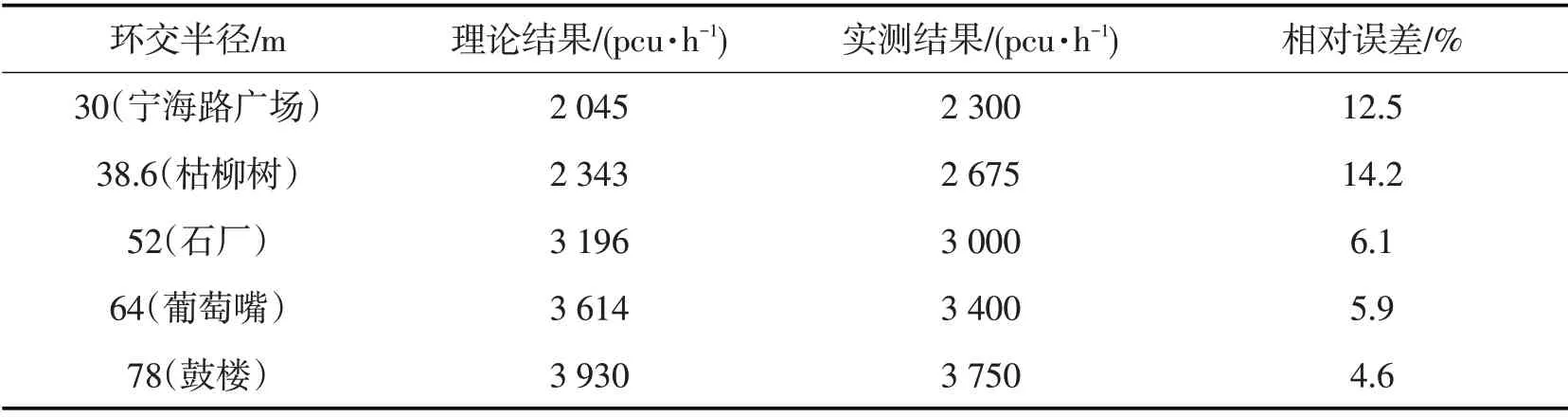
表3 实测模型验证Tab.3 The real verification of the model

2.3 模型的分析

通过以上分析，可以得出：交通量较小时，实测值比理论值小，主要原因在于此时车速较高，临界间隙值较大；交通量较大时，实测值比理论值大，主要原因在于此时环行车流速度较低，强制穿插比例有所增加，临界间隙值较小。

大多数情况下误差在10%以内，只有当环交半径较小时，才会出现较大误差。较大的误差可以归因于环交半径较小时，车辆强行换道行为并不明显，且交织理论公式更适用于大尺寸的环形交叉口。

该模型只计算了各进口道的左、右、直行车辆数比例为1∶1∶2的情况，利用该思想同样可以计算各个进口道上转向比例都不相同的情况。从整个模型的建立、输出结果及其验证来看，这样的模型是比较合理的，它更好的结合环形交叉口实际情况，考虑到环道上车辆强行换道等行为，提出适合中国特有交通运行特性的环形交叉口通行能力计算方法。

3 结论

该模型通过调查城市环形交叉口实际的道路条件以及车辆运行规律，以交织区的通行能力为基础，认为交织区为环形交叉口的瓶颈，并决定了整个环形交叉口的通行能力，更符合交叉口的实际交通流状况。考虑交织区车辆强行换道行为，引入串行排队理论，与Wardrop公式相结合，提出新的交织区通行能力计算方法来计算整个环形交叉口的通行能力，并通过VISSIM仿真软件对优化模型进行了验证，结果证明模型较原模型更为合理，能更好的适应平面环形交叉口的规划设计以及实际交通状况。对环形交叉口交织段的规划、设计、建设、管理等工程实践具有重要的指导意义。

不足之处在于模型是针对两车道四路环形交叉口的车辆运行规律而建立的，其使用有一定的局限性，针对其他复杂交通情况通行能力的模型还有待进一步研究。

[1] 王炜,过秀成.交通工程学[M].南京:东南大学出版社,2000:75-77.

[2] 孟祥燕,王国立,李文权.环形交叉口交织段通行能力的线性规划模型[J].交通标准化,2005(8):141-143.

[3] TRANSPORTATION RESEARCH BOARD.Highway capacity manual 2000[M].Washington D C,USA:National Research Council,2000:252-254.

[4] 郑建湖,林小惠,郑礼席,等.基于马尔可夫链模型的交通拥挤状态预测[J].交通标准化,2012(22):76-79.

[5] 刘宗明,贾志绚,李兴莉.基于灰色马尔科夫链模型的交通量预测[J].华东交通大学学报,2012,29(1):30-34.

[6] GU W,CASSIDY M J,LI Y.On the capacity of highway checkpoints: Models for unconventional configurations[J].Transportation research,2012,46(10):1308-1321.

[7] 郭瑞军.基于间隙接受理论的环形交叉口通行能力研究[D].北京:北京交通大学,2013.

[8] 翟颖,常玉林.基于Vissim仿真的公路环形交叉口中心岛半径优化设计[J].交通与计算机,2007,25(4):29-31.

[9] 王玮琪.北京市环形交叉口通行能力研究[D].北京:北京工业大学,2013.