信号交叉口驾驶员行为博弈分析

黄选伟，汪 晶，张 邻

（1.南昌工学院民族教育学院，江西 南昌330108；2.南昌航空大学数学与信息科学学院，江西 南昌330063）

交叉口是城市道路网络的结点，起着转换和协调交通流的重要作用[1]，如果运行不良则会影响整个交通系统的运行。随着城市化进程的加快，信号交叉口在整个网络交通控制中占住重要地位，而在绿灯结束期间，机动车驾驶员通过交叉口时的决策行为，直接影响着交叉口的交通安全，降低了路网的通行效率，因此研究绿灯结束期间驾驶员的决策行为，具有重要的现实意义。

国内外许多学者对驾驶员行为决策进行了研究［2-4］。Mutat Demir等［5］提出了一种驾驶模拟器为不同性格的驾驶员提供模拟驾驶环境，建立了驾驶员的行为模型，这能让驾驶员在一个安全的环境中练习驾驶，减少交通事故的发生；但是文中没有结合驾驶员的行为模型来评估驾驶模拟器的有效性，且驾驶模拟和现实的交通环境还存在很大差别。吴文静等［6］从驾驶员心理角度出发，分析驾驶员在交叉口处的决策过程，综合驾驶员行为的影响因素，在对交叉口数据采集和分析的基础上，运用Logistic 模型建立了在倒计时信号交叉口驾驶员决策行为模型。龙科军等［7］利用视频采集数据研究黄灯期间驾驶员决策行为，运用Logistic回归构建了驾驶员行为模型。这些模型将冲突车辆间驾驶员的决策行为均简化为“单次决策”，不能准确的刻画交叉口冲突车辆间驾驶员复杂的心理过程，忽略了冲突车辆间驾驶员决策行为的相互影响。刘小明等［8］虽然从更小时空尺度考虑无信号交叉口驾驶员插车行为，并建立了基于博弈论［9］的无信号交叉口驾驶员的决策行为模型，分析了不同驾驶员类型组合在插车博弈过程中的Nash 均衡，及相应的驾驶员行为，但是将驾驶员行为的决策简化为加速、减速2种，不够全面。

首先对交叉口驾驶员决策行为进行多时间段分析，考虑驾驶员性格因素，以及不同策略之间相对势因素，然后结合车辆到达停车线的时间与黄灯剩余时间的时间差，建立基于动态重复博弈的驾驶员决策行为模型，通过驾驶员在行进过程中的决策行为，分析驾驶员获得的效用，得到动态博弈中驾驶员的最优决策。

1 驾驶员决策行为分析

车辆通过信号交叉路口遇到黄灯亮时，若车辆已经越过停车线可以继续前进，若车辆未越过停车线应当停车；因此，车辆通过信号交叉口时，驾驶员需要判断车辆能否在黄灯亮之前越过停车线。如果判断失误，就会引起交通冲突，甚至造成交通事故；所以，在黄灯灯亮之前，驾驶员首先应判断车辆所处的状态以及预测到停车线的距离，然后通过加速、匀速、减速3种策略使车辆安全、快速地通过信号交叉口。

为了准确的描述驾驶员的决策行为，引入临界通过最大距离与临界停车最短距离，临界最大通过距离指的是驾驶员观察到红绿灯显示器时，车辆行驶的最大距离l1，可由下式表示。

式中：v0为车辆的速度，ty为绿灯剩余时间，a+max为车辆的最大加速度。

临界最短停车距离指的是黄灯开始时，车辆安全停车的最短距离l2，可由下式表示

式中：tj为驾驶员的操作时间，tf为驾驶员的反应时间，a-max为车辆的最大减速度。

图1所示为一双向6车道信号交叉口，N代表北，S代表南，W代表西，E代表东。对于直行车流，假设交叉口视野无遮挡，N→S方向有一个车辆C1且到停车线的距离为L，速度和加速度分别为v0和a0。

分析l1、l2、L的大小关系，确定C1所处的状态，当l1≤l2时，若L＜l1，由于车辆不能安全停车，C1能在红灯灯亮之前安全、快速地通过交叉路口；若l1≤L≤l2，C1不能安全通过交叉路口且不能安全停车；若L≥l2，由于车辆不能闯黄灯，C1必须减速停车；当l1＞l2时，若L＜l2，C1不能安全通过交叉路口且不能安全停车；若L≥l2，C1必须减速停车。

在现实生活中，车辆通过信号交叉口的情况十分复杂，驾驶员在驾驶过程中具有复杂的心理过程，为了能安全、尽快地通过信号交叉口，驾驶员必须进行一系列的决策。

令C1到停车线的距离为L的时刻为t0且绿灯亮了t秒，则绿灯剩余时间ts=ty-t，C1通过停车线的时刻 为tn，将t0→tn时 段 等 分 成n份，即车辆C1为了安全尽快地通过交叉口，C1的驾驶员在每一小时段的开始进行加速，匀速，减速决策。假设[ti-1,ti]小时段内C1的加速度为ai（i=1,2,3,…,n）且在每一小时段内车辆的加速度是恒定的，则C1在ti时刻的速度vi为

式中：Δt为每一小时段的时间长度；ai为每一小时段的加速度，i=1,2,3,…,n。ti时刻，绿灯剩余时间tis为

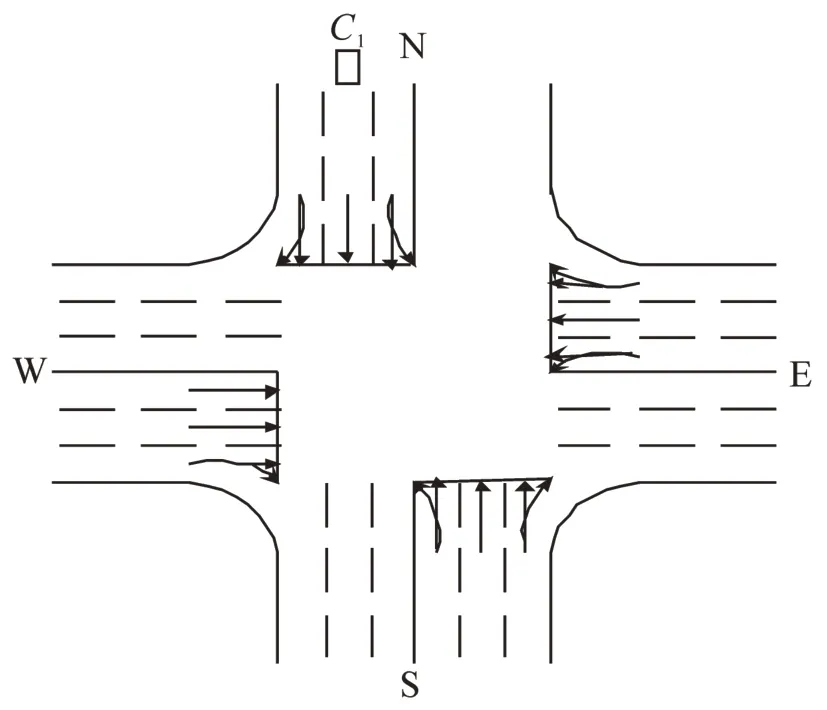
图1 信号交叉口示意图Fig.1 Diagram of signalized intersection

由式（3）与式（4）得出C1在t0→ti时段内行驶的路程Si，以及C1在ti时刻到停车线的距离Li，C1在ti时刻的临界通过最大距离l1i与临界停车最短距离li2

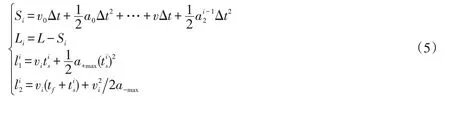
由式（5）与式（6）可知，ti时刻，C1到达停车线的时间Ti与绿灯剩余时间tis的时间差ΔTi为

综上所述，当l1i＜li2时，若Li＜l1i，车辆在黄灯灯亮之前不能安全停车，若ΔTi＞0，C1能在黄灯灯亮之前安全、快速地通过交叉路口，若ΔTi≤0，C1不能安全通过交叉路口且不能安全停车；若l1i≤Li≤li2，C1不能安全通过交叉路口且不能安全停车；若Li≥li2，由于车辆不能闯黄灯，C1必须减速停车；同理，当li2≤l1i时，若Li＜li2，若ΔTi＞0，C1能在黄灯灯亮之前安全、快速地通过交叉路口，若ΔTi≤0，C1即将闯黄灯，不能安全通过交叉路口；若Li≥li2，C1必须减速停车。

2 驾驶员决策行为模型的建立

信号交叉口的通行状况十分复杂，驾驶员会不断地改变决策行为，在此过程中，驾驶员首先要确定车辆所处的状态，预测车辆到停车线的距离Li，然后通过加速，减速，匀速三种策略使车辆安全、尽快地通过信号交叉口。车辆在通过信号交叉口的过程中，驾驶员均希望安全、尽快地通过交叉口，其中安全是首要因素；因此，可以从安全和时间两个方面来衡量驾驶员选择不同策略所得的收益或损失，即衡量驾驶员所得的效用。

车辆能不能通过信号交叉口，与C1到达停车线的时间和黄灯剩余时间的时间差ΔTi有关，当ΔTi＞0时，C1能安全、快速地通过交叉路口，ΔTi越大，驾驶员获得的效用Bi越大，即收益越大，此时Bi为正值；当ΔTi≤0 时，C1不能通过交叉路口，ΔTi越小，驾驶员获得的效用Ui越小，即损失越大，此时Ui为负值；因此，驾驶员的效用与ΔTi成正比，可设为Ui=±eΔTi。

令β为驾驶员的性格因子，0 ≤β≤1，并令0 ≤β≤1/3 对应的是谨慎型的驾驶员，1/3 ＜β≤2/3 对应的是温和型的驾驶员，2/3 ＜β≤1 对应的是冲动型的驾驶员，驾驶员的决策显然与驾驶员的性格有关。同时C1通过交叉口的临界最大距离l1i与临界停车最短距离li2也是影响驾驶员决策的因素之一，l1i越大，C1通过交叉口的可能性越大，li2越大，C1通过交叉口的可能性越小，因此驾驶员的效用与l1i成正比，与li2成反比，即与l1i li2有关。

此外，驾驶员获得的效用还与驾驶员的决策策略有关，令α为决策系数，不同的决策对应的决策系数也不同，即不同策略对应的势因素不同，如：C1的驾驶员选择加速策略的势为α1，选择减速策略的势为α2，则α1＞α2，即选择加速策略比选择减速策略有优势。

又由于当l1i＜li2时，若l1i≤Li≤li2，驾驶员不能通过改变策略而安全通过交叉路口且不能安全停车，此时，令驾驶员获得的效用为定值且为负值，可设为Ui=-e；同理，当Li≥li2时，由于车辆不能闯黄灯，驾驶员必须减速停车来避免闯黄灯，此时车辆获得的效用可令为Ui=e。

综上所述，驾驶员的效用Ui是ΔTi、α、β、l1i和li2的函数，即为Ui(ΔTi,β,l1i,li2)，可表示为

1）当l1i＜li2时

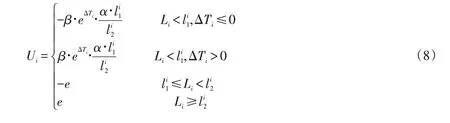
2）当l1i≥时

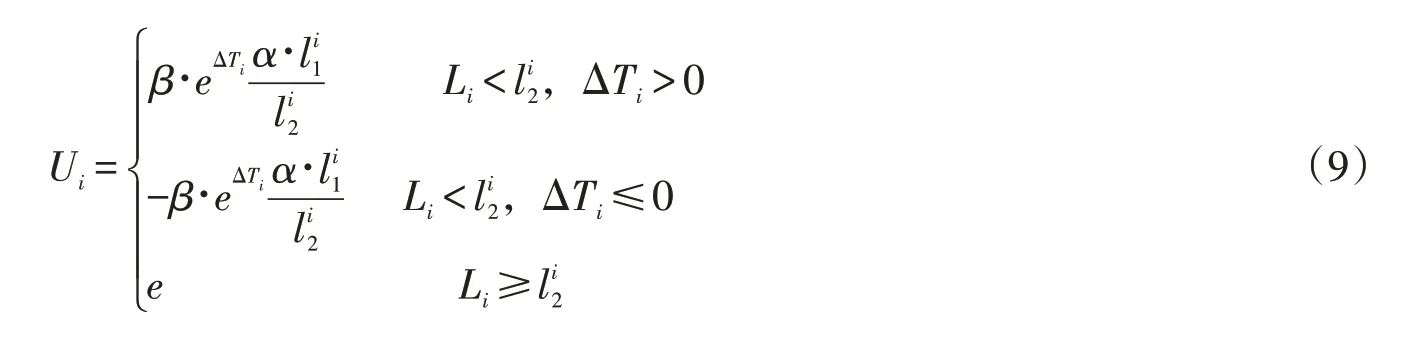
3 算例

假设每一时段的时间长度△t=1.5 s，令C1在ti时刻开始时到停车线的距离为：Li=140 m，速度为vi=45 km·h-1，加速度为ai=0，绿灯剩余时间为ty=5 s，并且在行进过程中，冲动型、温和型、谨慎型的驾驶员选择加速通过冲突点的加速度分别为a1=2 m·s-2，a2=1.5 m·s-2，a3=1 m·s-2，选择减速通过冲突点的减速度分别为a1=-1 m·s-2，a2=-1.5 m·s-2，a3=-2 m·s-2，其中i=1，2，…，k，冲动型、温和型、谨慎型的驾驶员对应的性格因子β分别为1，2 3，1 3，驾驶员选择加速、匀速、减速的决策系数α分别为4，3，2，驾驶员的反应时间和操作时间分别为0.5 s和1.5 s，车辆在紧急情况下的最大减速度大小为a-max=6 m·s-2，车辆的最大加速度为a+max=7 m·s-2[7]。根据式（8）式（9），可求得C1在ti+1时刻选择加速，匀速，减速策略时对应的效用值，均为2.718 3。

分析可知，在博弈开始时刻，不同性格类型的驾驶员所获得的效用均为2.718 3，表明此时，他们与交叉口的距离均大于临界停车最短距离，由于不能闯黄灯，他们必须选择停车等待。图2～图4分别表示不同性格类型驾驶员的不同策略对应效用变化趋势。以冲动型的驾驶员选择加速、匀速、减速策略为例，如图2所示，若冲动型驾驶员选择加速策略，在时刻1到时刻4期间，驾驶员获得的效用值始终保持在2.718 3，处于稳定趋势，时刻4到时刻5期间，效用值呈下降趋势，且到达下峰值-19.475 5，时刻5到时刻10期间，效用值呈上升趋势且逐渐趋于稳定，在整个时间段内，驾驶员的效用值在时刻4的变化最为突出，其改变决策行为的可能性最大，且在前3个时间段内，车辆与交叉口的距离均大于临界停车最短距离，驾驶员最可能选择停车等待，时刻4到时刻8期间，驾驶员的效用值由正转到负，说明车辆按现行的车速和加速度不能安全地通过交叉路口，时刻8之后，车辆能在黄灯灯亮之前，安全、快速的通过交叉路口；若冲动型驾驶员选择匀速策略，在前2个时间段内，驾驶员获得的效用值始终保持在2.718 3，处于稳定趋势，时刻3到时刻4期间，驾驶员的效用值呈下降趋势，且到达下峰值-2.718 3，时刻4到时刻7期间，驾驶员的效用值在-2.718 3左右波动，基本趋于稳定，时刻7到时刻8期间，驾驶员的效用值呈上升趋势，时刻8之后，驾驶员的效用值在-0.230 0左右波动且基本趋于稳定，在整个时间段内，驾驶员的效用值在时刻3变化最为突出，驾驶员改变其决策行为的可能性最大，且在在前2个时间段内，车辆与交叉口的距离均大于临界停车最短距离，驾驶员最可能选择停车等待，时刻3到时刻10期间，驾驶员的效用值由正转到负，说明车辆按现行的车速和加速度不能安全地通过交叉路口。同理，可以分析驾驶员选择减速策略时，驾驶员获得的效用值的变化趋势，由分析比较冲动型驾驶员选择不同策略对应的效用值的变化趋势知，驾驶员在决策开始时刻选择减速策略获得的效用值最大，安全通过交叉口的可能性也最大；因此，对于冲动型的驾驶员在决策初始时刻最可能选择减速策略。

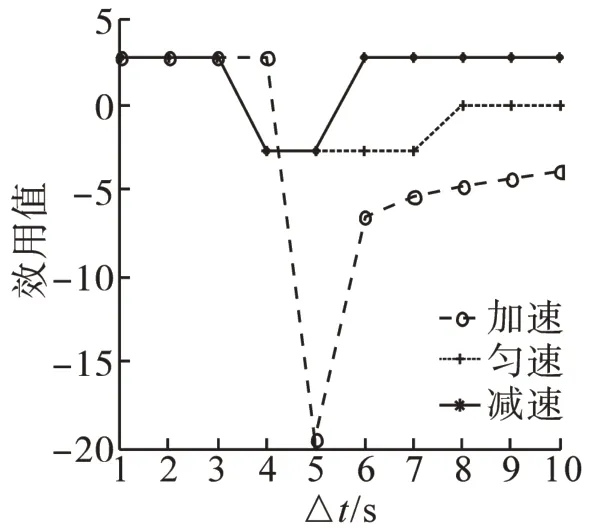
图2 冲动型驾驶员选择不同策略的效用值Fig.2 Utility values of impulse drivers choosing different strategies

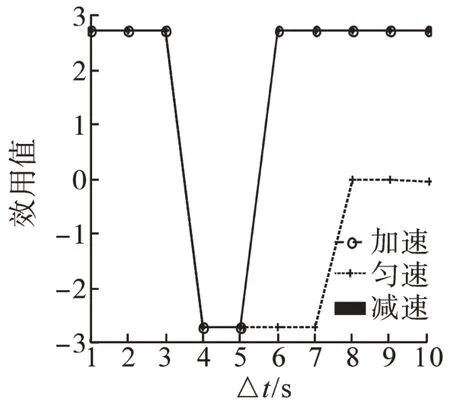
图3 温和型驾驶员选择不同策略的效用值Fig.3 Utility values of mild drivers choosing different strategies

同理分析温和型、谨慎型驾驶员选择不同策略对应效用值的变化趋势知，温和型的驾驶员选择加速或减速策略时获得的效用值最大，安全通过交叉口的可能性最大；谨慎型的驾驶员选择减速策略时，驾驶员安全通过交叉口的可能性最大。

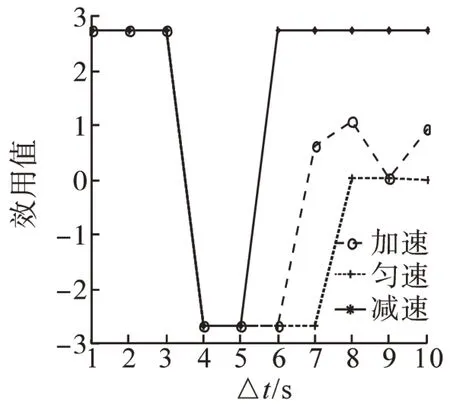
图4 谨慎型驾驶员选择不同策略的效用值Fig.4 Utility values of cautious drivers choosing different strategies

4 结束语

根据机动车驾驶员的性格因素和不同策略间的相对势因素，从博弈角度对驾驶员的决策行为进行多时段分析，结合车辆到达停车线的时间与黄灯剩余时间的时间差，建立了基于动态重复博弈的驾驶员决策行为模型，最后应用本文模型分析算例，计算不同驾驶员性格类型的效用，得到动态博弈中机动车驾驶员的最优决策行为，并对博弈过程中不同性格类型的驾驶员选择不同策略时的效用变化趋势进行了分析，得到冲动型的驾驶员偏好于选择减速策略，温和型的驾驶员偏好于选择加速或减速策略，谨慎型的驾驶员偏好于选择减速策略。

本文在一定程度上能够反映在绿灯结束期间，机动车驾驶员通过信号交叉口时复杂的驾驶心理，为研究信号交叉口驾驶员决策行为提供理论参考，但在建模过程中只考虑了单一车型和一辆车参与博弈，并且对影响模型的相关因素进行了相应的简化，更为合理的多车、多车型博弈模型，需要做进一步研究。

[1]张笑彬,郑长江,郑树康.预信号交叉口公交停靠站与人行横道协调设计[J].华东交通大学学报,2014,31(1):23-28.

[2]ALEXANDRA GHEORGHIU, CORNELIU HAVÂRNEANU.Driving behavior of a sample of young Romanian drivers[J].Procedia-Social and Behavioral Sciences,2011(33):697-701.

[3]CASUCCI M, MARCHITTO P C, CACCIABUE A.Numerical tool for reproducing driver behaviour: experiments and predictive simulations[J].Original Research Article Applied Ergonomics,2010,41(2):198-210.

[4]NAOHIRO UCHIYAMA EIICHI TANIGUCHI.A study of dispatcher′s route choice model based on evolutionary game theory[J].Procedia-Social and Behavioral Sciences,2012(39):495-509.

[5]MURAT DEMIR,ABDULLAH CAVUSOGLU.A new driver behavior model to create realistic urban traffic environment[J].Transportation Research Part F,2012(15):289-296.

[6]吴文静,隽志才,贾洪飞,倒计时信号交叉口处的驾驶员行为决策[J].系统工程与实践,2009,29(7):160-165.

[7]龙科军,何林儒,韩立,黄灯期间信号交叉口的驾驶员行为[J].系统工程,2010,28(12):117-120.

[8]刘小明,王秀英.基于重复博弈的无灯控交叉口驾驶员行为模型[J].中国公路学报,2011,24(4):94-100.

[9]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2012:97-103.