小学生数学思维结构化培养策略初探
江苏建湖县第二实验小学(224700) 孔祥林
小学生数学思维结构化培养策略初探
江苏建湖县第二实验小学(224700) 孔祥林
在小学数学教学中,要让学生真正形成数学的思维,教师必须对学生进行思维结构化培养。从小处入手层层突破、新旧知识有机结合、感性演绎引发量变三方举措,提高了学生思维的有序性、系统性和深刻性,促进了学生思维的结构化。
小学生 数学思维 结构化
小学数学教学的本质是思维训练,通过思维训练,帮助学生建立应激机制,运用数学思维解决实际生活中的问题。在小学六年的学习中,小学生的思维水平都会有一定程度的提高,对于数学教师来说,教学中除了要培养学生思维的逻辑性、指向性之外,还要促进学生数学思维的结构化形成。那么如何实现学生数学思维的结构化呢?
一、小处入手层层突破,提高思维的有序性
对于大多数小学生来说,在思维发展初期其思维往往混乱无序,解决问题时不知如何下手。针对这个现状,教师在教学中立足于学生的思维水平,从学生最容易解决的小问题入手,层层剥笋,由小到大,一步步有序突破,从而达到解决大问题的目的。
如在教学“倍数与因数”时,有这样一道习题:找出2的倍数。学生按部就班地写下去:2,4,6,8,10,12,我追问:为什么这样找?(因为2的1倍是2,2的2倍是4,2的3倍是6,2的4倍是8,2的5倍是10,2的6倍是12)能找得完吗?(找不完。2的倍数有无数个)2的最小倍数是几?2的最大倍数是几?(2的最小倍数是2,2没有最大倍数)根据这一连串的问题,学生经过思考与讨论后,对一个数的倍数和因数的特征有了全面清晰的认知,从而获得规律:一个数的最小倍数是这个数本身,一个数的倍数有无限个,一个数没有最大倍数。在这过程中学生理清了混乱的思维,达到解决问题的目的,实现了有序思维。
二、新旧知识有机结合,提高思维的系统性
当学生在解决问题的过程中,往往会陷入孤立状态,导致认识问题主观片面,容易犯以偏概全的错误。这就需要教师在教学中设置有效问题,引导学生联系以往的知识,将新旧知识结合起来,这样一方面可有效克服负迁移,另一方面则促进知识的正迁移,为学生积累数学活动经验创造条件。
如在教学“能被3整除的数”时,我引导学生复习旧知,借此发现其中的规律:能被2整除的数有哪些特征?(个位上的数是0,2,4,6,8)能被5整除的数有什么特征?(个位上的数是0,5)猜想一下,能被3整除的数有什么特征?学生因为有旧知的铺垫,猜想如前面的规律一样,能被3整除的数个位上的数是3,6,9,即个位上的数能被3整除。事实是否如此呢?我先让学生写出答案来一一验证,很快学生发现,个位上的数不是3、6、9时也能被3整除,如27,而个位上是3、6、9的有些也不能被3整除,如19。此时我继续提出问题:想一想,我们在研究能被2和5整除的数的特征时,是用什么方法的?能否采用这样的方法继续探究能被3整除的数的特征?
经过问题引导,学生否定了之前的猜想,确认了不能将“能被2和5整除的数的特征”套用在“能被3整除的数的特征”上面,从而排除了新旧知识的负迁移干扰,同时,又确认了旧知探究中使用的方法——在百数表里先圈出符合条件的数,然后观察后找出规律。据此,学生学会了运用同样的方法进行新知探究,从而促进了思维的系统性。
三、感性演绎引发量变,提高思维的深刻性
教师要培养学生思维的深刻性,就要根据教学进程及教学内容设置感性积累环节,在丰富的表象积累基础上,引导学生运用推理和归纳进行反思,训练学生的总结和应用能力,使学生的思维获得质的飞跃。
如在教学“轴对称图形的对称轴”时,关于对称轴的认识,大多数学生无法建立直观概念,容易流于表面。很多教师在教学时往往忽略思维引导的过程,直接灌输给学生图形的对称轴的条数,甚至有些干脆让学生死记硬背。这样的教学策略影响了学生思维的深刻性,更损害了学生思维的自主性。
为了让学生获得丰富的感性积累,我特意要求学生通过动手折纸或者画图得到如下正多边形,学生头脑中建立了丰富的表象,在此基础上设置问题:说说每个图形中有几条对称轴?为什么?(学生指出,正三角形有3条对称轴,正方形有4条对称轴,正五边形有5条对称轴,正六边形有6条对称轴)观察图形列出表格,并填写表格,思考一下对称轴和图形有什么关系,你发现了什么。学生填写表格观察后得出结论:正几边形就有几条对称轴。我继续设置问题:任意多边形都有这个特征吗?观察这些图形的边角,有什么特征?你能举例来证明这个结论的正确性吗?(学生画出正八边形并指出其中的8条对称轴)此时我引出正多边形的概念,并带领学生归纳正多边形边数与对称轴条数的关系,然后探究圆有几条对称轴,半圆有几条对称轴。由此,学生的感性积累达到量变,思维由浅入深,逐步从感性演绎过渡到抽象概括,体现出思维的深刻性。
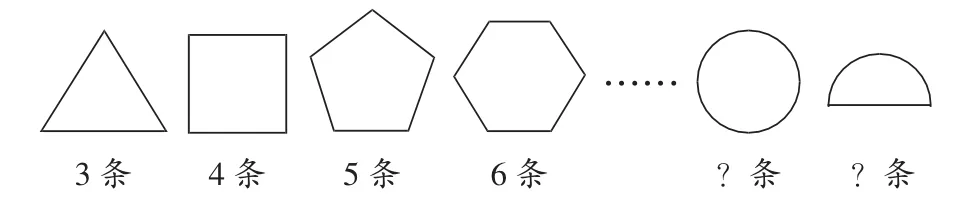
在以上教学环节中,学生通过观察和实践,不但能够发挥个体能动性,经过自主思考从中找出规律性的知识来,而且在总结和反思的基础上,能够直观有效地把握新知,从表象的知识形态逐步过渡到抽象的知识领域中去。
总之,在小学数学教学中,要使学生真正形成数学思维,就要拓宽学生的数学空间,促进学生思维的结构化,这是每一个数学教师的努力方向。
(责编 黄春香)
G623.5
A
1007-9068(2015)05-074

