评价:错因诊断与改进策略探索
——对小学数学毕业班阶段性考试错题的理性分析
江苏南师附中仙林学校小学部(210023) 饶道松
评价:错因诊断与改进策略探索
——对小学数学毕业班阶段性考试错题的理性分析
江苏南师附中仙林学校小学部(210023) 饶道松
《数学课程标准》(2011版)中指出:“评价的主要目的是全面了解学生数学学习的过程和结果,激励学生学习和改进教师教学。因此,教师应通过考试的诊断评价分析,了解学生数学学习已经达到什么样的水平,还存在哪些薄弱环节,以便及时调整教学内容、教学方法与策略,最终实现有效教学之目的。
小学数学 评价 诊断 改进
《数学课程标准》(2011版)中指出:“评价的主要目的是全面了解学生数学学习的过程和结果,激励学生学习和改进教师教学。”基于此,教师应把考试评价作为提高教学针对性和有效性的途径,充分利用考试评价诊断学生的错因,改进自己的教学。下面,笔者以近期毕业班阶段性考试的部分错题为例,谈谈如何利用错例诊断,实现有效教学。
一、重视基础知识,感悟概念本质
例1.(判断)一件衣服打五折销售正好可以保本,那么不打折销售就可以获得50%的利润。( )
例2.平行四边形相邻两条边分别是6厘米、4厘米,量得一条边上的高是5厘米,这个平行四边形的面积是( )平方厘米。
错例诊断:对于例1,很多学生认为是正确的,通过访谈知道,学生错误的原因主要有以下两点:第一,“打五折销售”就是以一半的价钱销售,另外一半就是利润,也就是50%;第二,学生举例,如原价200元,打五折销售是100元,利润是(200-100)÷200=50%。显然,从上述分析中可知,学生没有弄清楚百分数应用的基本概念。
对于例2,有部分学生只知道平行四边形的面积等于底乘高,至于是哪条底边所对应的高就不甚了解了。显然,学生对于概念的理解属于“知其然,不知其所以然”的类型。
改进建议:以上两个例子,考查的是对基本概念的应用。对于例1中百分数的应用,关键是找单位“1”的量,这里没有明显的标志,导致学生无从下手解决问题。找单位“1”的量要认准谁和谁比,被比的那个量就是单位“1”的量,所以平时学生需要进行这方面的大量练习。
在例2的教学中,首先要引导学生树立画图的意识。有少部分学生在图画好后,立即就知道自己的错误所在了,而剩下的学生对于“直线外一点到直线之间的距离,垂直线段最短”这一概念不理解。教师教学时需要结合具体的情境,引导学生去探索、去感悟,使学生深刻理解概念的内涵。
二、重视基本技能,掌握基本方法
例3.东东记得李叔叔的电话号码是806415□□,同时还记得最大数字是8,各个数字又不重复,东东要拨通李叔叔的电话,最多要打( )次。
例4.如右图,阴影部分的两个小正方形周长和为4.8分米,那么大正方形的边长是( )分米。
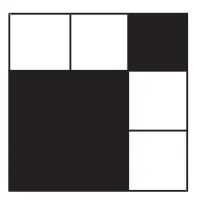
错例诊断:这两类题目在教学中都练习过不少,但是学生在复习阶段进行的阶段性测试中仍然出错。有的教师认为是训练还不够多,需要进一步强化练习。教师在评析例3前,可让学生先思考这样一道题:“用1、2、3三个数字写出不同的两位数,一共可以写出几个?请你罗列出来。”大部分学生都能写出正确答案,可为什么例3这题还有学生不会呢?在例4中,有相当多的学生不知道阴影部分的两个小正方形与大正方形周长之间的关系,还有相当一部分学生是用4.8÷12=0.4(分米)求出一个最小正方形的边长,然后列式计算大正方形的边长为0.4×3=1.2(分米)。可是,当右图出现时,该怎么办呢?相当部分学生没有办法解答。笔者分析学生出现上述错误的原因,发现是教师在平时的教学中,缺乏在具体的情境中对学生进行基本技能和方法的指导,导致学生在反复机械训练的过程中很难形成基本技能和掌握基本方法。

改进建议:例3这类题看似比较简单,但教师也需要在具体的情境中教给学生一定的方法和技能。如先确定方框中可以填哪些数字,然后进行分类,最后按照一定的次序一一列举,从而做到不重复、不遗漏。
例4这道题,关键是引导学生利用转化的策略,体会大正方形周长与两个小正方形周长和之间的关系。教学时,教师应组织学生进行操作活动,让学生在具体的操作过程中体会转化的策略,学会转化的操作技能和方法,切身感受到原来大正方形的周长与两个小正方形周长和是相等的。学生在探索的过程中,教师应给予适时的点拨,引导学生归纳总结解决问题的思路和方法,培养学生数学思考的能力。
三、充分展示交流,学会数学思考
例5.一张长方形纸长12分米,宽7.5分米。最多可以剪成( )个直角边分别为4分米和3分米的直角三角形。
A.15 B.14 C.12
错例诊断:学生在解答例5时存在很多的错误,全班28名学生,有4名学生选择B,让其分析时都说是随便选的,不知道怎么做。于是,可能有教师认为学生平时的训练太少,导致能力得不到提升。然而,笔者认为学生做错的关键原因是教师只针对题目教给学生方法,没有引导学生在思维碰撞中学会思考,习得方法。
改进建议:对于例5,不同的学生有不同的思考。教学中,教师应充分展示学生的思维过程,即使是错误的思考也应该展示。对于这道题,学生有三种不同的解答方法:第一种方法,先算出长方形的面积,12×7.5=90(平方分米),再算出三角形的面积为4×3÷2=6(平方分米),最后用长方形的面积除以三角形的面积得出三角形的个数,即90÷6=15(个)。第二种方法,先用长方形的长除以三角形一条直角边长度,得出可以放几个三角形,即12÷4=3(个);同理,宽可以放两个,即7.5÷3≈2(个),最后用3×2×2=12(个)求出三角形的个数。第三种方法,可以用画图的方式表示,通过画图(学生展示两种不同的画法,图1是以上第二种解法,而图2才是适合本题的剪法),学生容易知道最多可以剪成14个这样的三角形。

图1
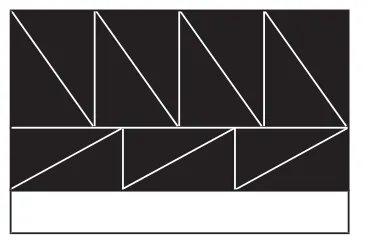
图2
在特定的条件下,这三种方法都可以解决此类问题,只是有部分学生没有真正学会思考。可见,学生的认知水平是有差异的。那么,如何让“不同的人在数学上获得不同的发展”呢?其实,《数学课程标准》中已经给了提示,即可以先让学生独立思考,主动探索解决问题的方法;然后让学生进行小组交流,发表个人的看法;最后让不同层次的学生阐述自己的思考,在不断的交流中,促使不同学生的思维相互碰撞、相互启发,从而逐步培养学生的思辨能力,使学生学会思考。
四、积累活动经验,提升数学素养
例6.一只装有红漆的圆柱形漆缸,高是20厘米,底面积是80平方厘米,漆深8厘米。现将一个高是20厘米的长方体铁棒(底面是边长4厘米的正方形)竖直插到漆缸底部,然后抽出。铁棒被染红部分的面积是多少?
错例诊断:此题是本次考试中失分最多的一道题,这样的题目有一定的难度,但在复习的过程中讲练也不少,可是结果不尽如人意。同年级的教师普遍认为,学生的空间想象能力和逻辑思维能力薄弱,究其深层次的原因,应该是学生缺乏基本活动经验的积累。
改进建议:此类问题通常有两种情况:一种情况是物体浸没在液体中致液体升高;另一种情况,就是像本题一样非浸没状态致液体升高。第一种情况,学生有大量的生活经验,课堂上也做过相关的实验,积累了一定的活动经验,认识到液体上升的体积就是物体的体积。学生有了这样的经验后能很容易解决问题,那学生为什么对这道题不“情有独钟”呢?到底是哪道坎未能迈过呢?原来是学生不仅缺乏生活经验,更缺乏活动经验的积累。如果课堂上教师让学生进行实验操作,启发学生思考,积累活动经验,学生就不会出现这样的结果了。可让学生进行以下实验:第一,在装有半杯水的圆柱形玻璃杯中垂直插入一根长方体玻璃棒;第二,引导学生观察发现“水面升高了,水的体积没有变”;第三,思考交流“为什么水面升高了,体积没有变呢”。在教师的智慧点拨之下,学生渐渐明白原来水的底面积变小了。学生在具体的操作活动中学会思考的方法,自然就积累了相应的数学活动经验,解决本题就不难了。
综上所述,通过考试的诊断评价分析,可以了解学生数学学习已经达到什么样的水平、还存在哪些薄弱环节,帮助教师不断总结、反思以及调整教学内容、教学方法与策略,最终实现有效教学之目的。
(责编 杜 华)
G623.5
A
1007-9068(2015)05-052

