Performance of a quasi-steady model for hovering hummingbirds✩

Jilei Song，Hoxing Luo，∗，Tyson L.Hedrick

aDepartment of Mechanical Engineering，Vanderbilt University，2301 Vanderbilt Pl.，Nashville，TN 37235，USA

bDepartment of Biology，University North Carolina at Chapel Hill，Chapel Hill，NC 27599，USA

Performance of a quasi-steady model for hovering hummingbirds✩

Jialei Songa，Haoxiang Luoa，∗，Tyson L.Hedrickb

aDepartment of Mechanical Engineering，Vanderbilt University，2301 Vanderbilt Pl.，Nashville，TN 37235，USA

bDepartment of Biology，University North Carolina at Chapel Hill，Chapel Hill，NC 27599，USA

A R T I C L E I N F O

Article history：

Received 30 October 2014

Accepted 3 November 2014

Available online 6 January 2015

Animal flight

A quasi-steady model describing aerodynamics of hovering Ruby-throated hummingbirds is presented to study extent of the low-order model in representing the flow physics of the bird and also to separately quantify the forces from the translational，rotational，and acceleration effects.Realistic wing kinematics are adopted and the model is calibrated against computational fluid dynamics（CFD）simulations of a corresponding revolving-wing model.The results show that the quasi-steady model is able to predict overall lift production reasonably well but fails to capture detailed force oscillations.The downstroke-upstroke asymmetry is consistent with that in the previous CFD study.Further analysis shows that significant rotational force is produced during mid-stroke rather than wing reversal.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

The aerodynamics of hovering hummingbirds has been investigated in several recent studies［1］.In general，hummingbirds utilize similar aerodynamic mechanisms as many insects for lift production，e.g.，presence of a leading-edge vortex over the wing surface.Previous studies have mostly focused on measurement of the flow around the bird using techniques such as particle image velocimetry（PIV）［2-4］.The lift production was directly studied more recently by Song et al.［5］，who performed a three-dimensional simulation of a Ruby-throated hummingbird（Archilochus colubris）based on reconstructed wing kinematics fromhigh-speed imaging data.

Aside from full computational fluid dynamics（CFD）models，the quasi-steady method，which assumes that the state of the system ata particular time is notaffected by its history，has long been used for the analysis of flapping wings［6］.This method later has been revised to include the translational force，rotational force，and acceleration effect to address the unique features of flapping wings［7，8］.Compared with full CFD models，the quasi-steady method cannot provide information about the three dimensional（3D）flow pattern and its prediction of force characteristics has limited accuracy.However，this method is extremely efficient in contrast with time-consuming 3D simulations，and it can be used as a complementary tool for fast analysis，e.g.，in optimization design［9］or study of flight maneuvers.

In this study，we will compare force prediction of a calibrated quasi-steady model for the same hummingbird with that of the corresponding CFD model in Ref.［5］，and we will use this simple model to further quantify the translational，rotational，and acceleration effects of the wing within a stroke cycle.These effects can not be easily decoupled in a full CFD simulation.

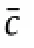
In the quasi-steady or blade-element model（BEM），the total force on the wing is summation of the forces on a set of chordwise strips，or blade elements，as shown in Fig.1（b）.A total of 39 strips are used in this work.For each chord strip，the translational velocity，rotational velocity，and angle of attack are obtained from the reconstructed wing kinematics.The total force on each strip is composed of three components:the translational force，d Ftrans，the rotational force，d Frot，and the added-mass effect（or the acceleration effect），d Facc，based on the formula in Ref.［8］if we ignore other effects such as wake capture and vortex shedding.Thus，the total force on the entire wing is

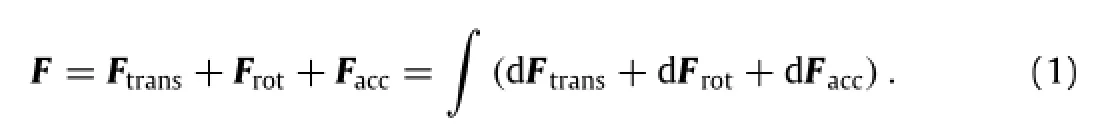
Next，we describe each component in this equation.

First，the translational force of a blade element consists of steady lift and drag that are functions of the angle of attack，α，defined as the angle between the element and the average stroke plane.Thus，the total translational force on the wing is

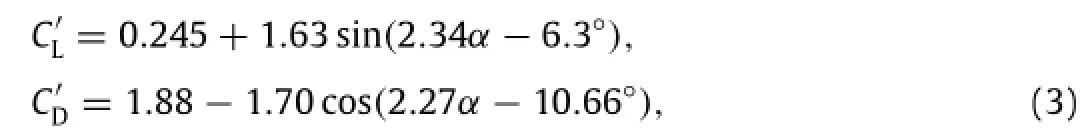
whereαis in degrees.Note that the constants in Eq.（3）are only accurate for the hummingbird wing or wings with similar geometry and Reynolds number.

The rotational motion，or pitching，around the long axis of the wing can enhance magnitude of the bound circulation，thus increasing lift force if it is combined with proper wing translation and angle of attack.We adopt the following formula for the rotational force［8］

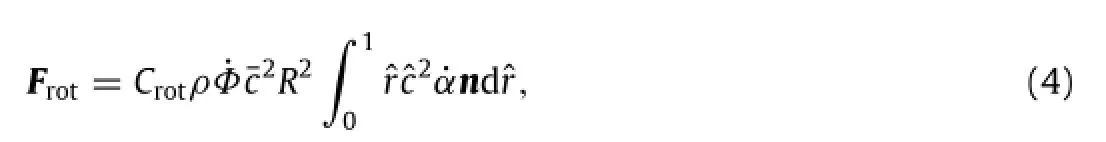
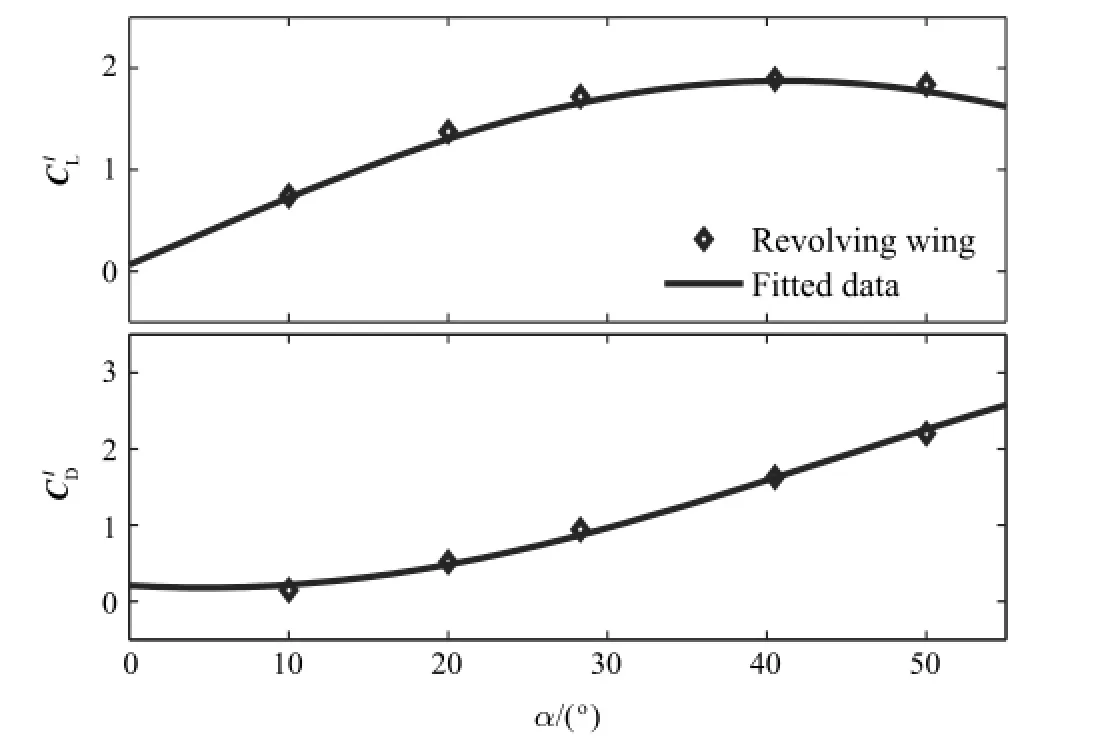
Fig.2.Data fitting for，whereα=10°，20°，28°，40°，50°is used for the revolving-wing simulation.

The force model due to the acceleration effect is based on that in Ref.［11］.Since the location of the pitching axis in the current model is determined specifically for the hummingbird，we re-scale the pitching acceleration termand obtain the following formula for the acceleration force

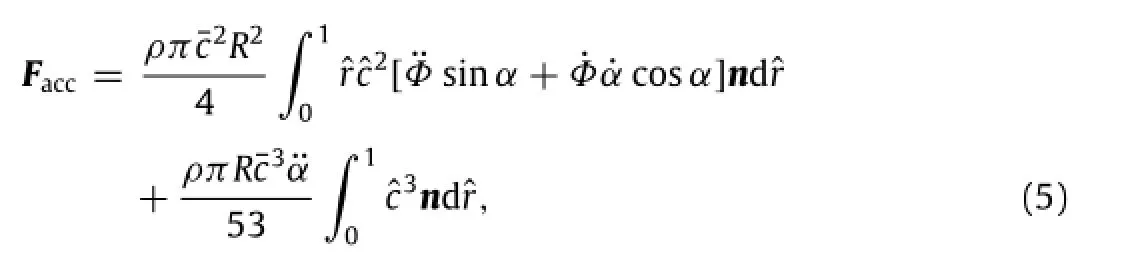
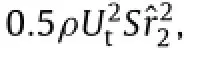
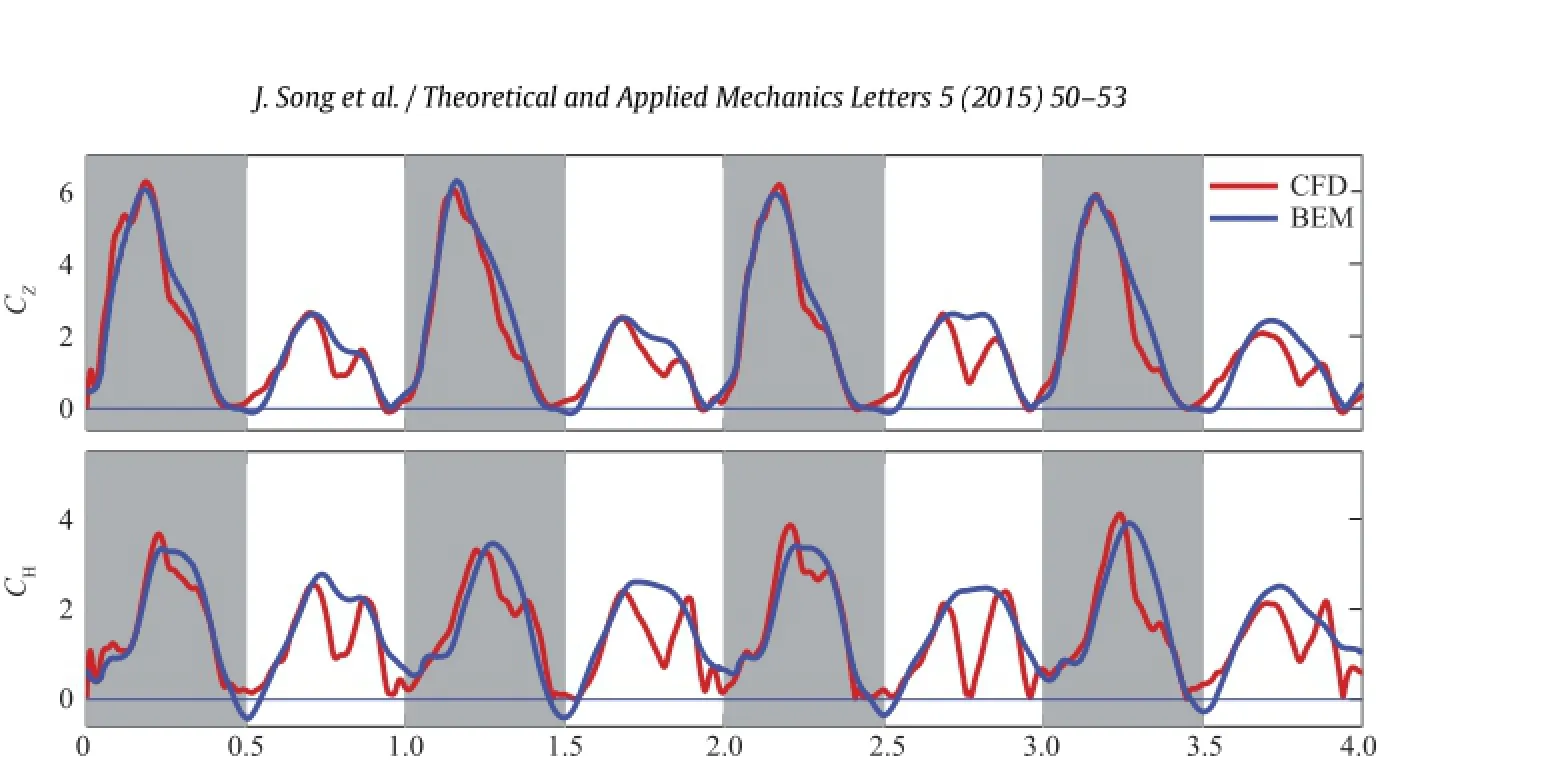
Fig.3.（Color online）Normalized vertical and horizontal forces，CZand CH，given by the BEM prediction and the CFD simulation.Shaded regions represent downstroke.

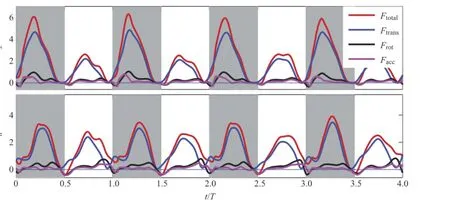
Fig.4.（Color online）Breakdown of forces as predicted by the BEM.

Table 1Quantitative comparison of the force coefficients between the BEM and CFD results，where‘‘down''means downstroke and‘up''means upstroke.

The quantitative comparison of the forces is shown in Table 1，where the mean and RMS differences are listed for downstroke，upstroke，and the whole cycle.It can be seen that the mean error within an entire stroke cycle is about 3%for the vertical force and less than 7%for the horizontal force.On average，the BEM predicts 94%of weight support，which is slightly higher than the CFD result，which is 91%of weight support.The remaining weight support could be accounted for by the camber effect thatis notmodeled［5］. The mean errors for upstroke are greater and are within 15%for downstroke and 25.1%for upstroke.More significant is the RMS error，which reaches nearly 26%for the vertical force and nearly 43%for the horizontal force.For upstroke，the RMS errors are even greater partly because the base numbers are smaller.

Since the average forces predicted by the BEM are reasonably close to those given by the CFD，we move on to study the translational，rotational，and acceleration forces as predicted by the BEM.Figure 4 shows breakdown of these force components. The quantitative information is provided in Table 2.It can be seen that the translational force dominates the force production by contributing to 82.4%of the vertical force and to 80.8%of the horizontal force.The rotational and acceleration effects have much lower contributions to the force production.The rotational effect explains only 11.8%and 13.8%for the verticaland horizontalforces，respectively，while the acceleration effect explains 5.8%and 5.4% for the vertical and horizontal forces，respectively.

The downstroke-upstroke ratio of the vertical force was reported to be 2.5 in the CFD simulation［5］.This asymmetry is also captured by the BEM result as shown in Fig.3，and the ratio is 2.34 from Table 1.Table 2 further shows that the translational，rotational，and acceleration effects all contribute to the asymmetry in the vertical force，and their own asymmetry ratios are all above two.In comparison，the asymmetry in the horizontal force is much smaller.By projecting the forces in the directions perpendicular and parallel to the instantaneous wing translation as illustrated in Fig.1（a），we obtain aerodynamic lift and drag，FLand FD.The BEM result shows that during downstroke，the drag contributes to nearly 20%to the vertical force and has a significant effect on the downstroke-upstroke asymmetry.This result is consistent with the report of the previous CFD study［5］.

The quasi-steady model calibrated against the CFD result can predict the general force characteristics within a stroke cycle and the mean forces reasonably well，even though the force oscillations due to 3D and unsteady effects are not captured.The force breakdown shows that the translational effect is dominant in force production.This model may be used in the future，of course with caution，for analysis of unsteady flight dynamics and flight control of the hummingbird［12］.

Table 2Normalized forces due to the wing translation，rotation，and acceleration effects.The numbers in the parentheses represent the percentage of the force within the total force.

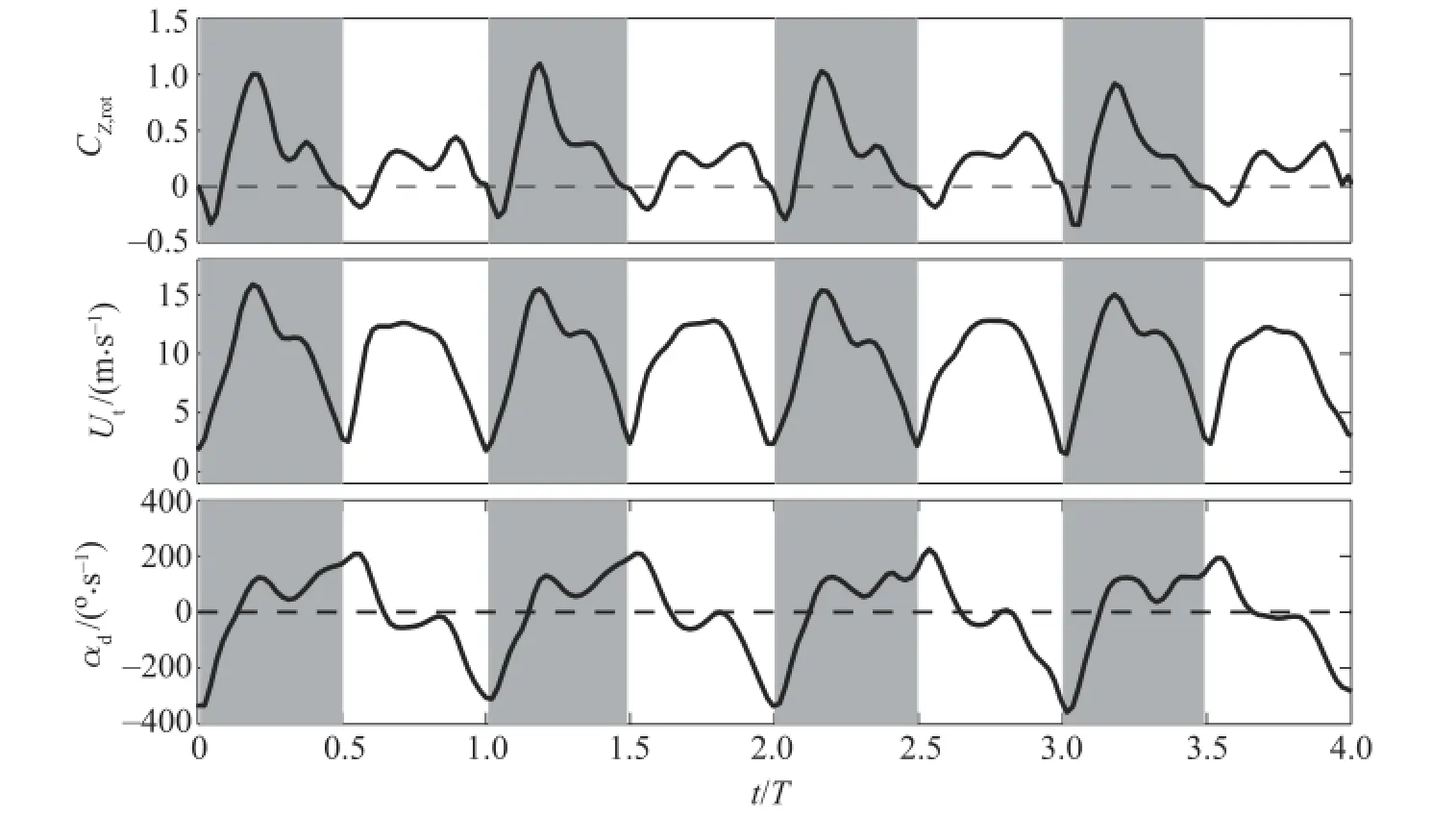
Fig.5.Histories of the normalized rotational force in the vertical direction，CZ，rot，wing tip velocity，and pitching velocity of the distal wing.

Acknowledgment

This work was supported by the National Science Foundation under CBET-0954381 to H.Luo and IOS-0920358 to T.L.Hedrick.

［1］B.W.Tobalske，D.R.Warrick，C.J.Clark，D.R.Powers，T.L.Hedrick，G.A.Hyder，A.A.Biewener，Three-dimensionalkinematics ofhummingbird，J.Exp.Biol.210（2007）2368-2382.

［2］D.R.Warrick，B.W.Tobalske，D.R.Powers，Lift production in the hovering hummingbird，Proc.R.Soc.B 276（2009）3747-3752.

［3］D.L.Altshuler，M.Princevac，H.Pan，J.Lozano，Wake patterns of the wings and tail of hovering hummingbirds，Exp.Fluids 46（2009）835-846.

［4］M.Wolf，V.M.Ortega-Jimenez，R.Dudley，Structure of the vortex wake in hovering Anna's hummingbirds（calypte anna），Proc.R.Soc.B 280（1773）（2013）20132391.

［5］J.Song，H.Luo，T.L.Hedrick，Three-dimensional flow and lift characteristics of a hovering ruby-throated hummingbird，J.Roy.Soc.Interface 11（2014）20140541.

［6］M.F.M.Osborne，Aerodynamics of flapping flight with application to insects，J.Exp.Biol.28（1951）221-245.

［7］M.H.Dickinson，F.Lehmann，S.P.Sane，Wing rotation and the aerodynamic basis of insect flight，Science 284（1999）1954-1960.

［8］S.P.Sane，M.H.Dickinson，The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight，J.Exp.Biol.205（2002）1087-1096.

［9］L.Zheng，T.L.Hedrick，R.Mittal，A multi-fidelity modeling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight，J.Fluid Mech.721（2013）118-154.

［10］T.L.Hedrick，B.W.Tobalske，I.G.Ros，D.R.Warrick，A.A.Biewener，Morphologicaland kinematic basis ofthe hummingbird flightstroke:scaling offlightmuscle transmission ratio，Proc.R.Soc.B 279（2012）1986-1992.

［11］S.P.Sane，M.H.Dickinson，The controlofflightforce by a flapping wing:liftand drag production，J.Exp.Biol.204（2001）2607-2626.

［12］T.L.Hedrick，B.Cheng，X.Deng，Wingbeat time and the scaling of passive rotational damping in flapping flight，Science 324（2009）252-255.

✩A preliminary version of this paper was presented at the 2014 AIAA Fluid Dynamics Conference.

∗Corresponding author.

E-mail address：haoxiang.luo@vanderbilt.edu（H.Luo）.

Hummingbird aerodynamics

Quasi-steady model

*This article belongs to the Fluid Mechanics