Experimental study on vortex induced vibration（VIV）of a wide-D-section cylinder in a cross flow

Qingyang Wang，Mogeng Li，Shengjin Xu

School of Aerospace Engineering，Tsinghua University，Beijing，China

Experimental study on vortex induced vibration（VIV）of a wide-D-section cylinder in a cross flow

Qingyang Wang，Mogeng Li，Shengjin Xu∗

School of Aerospace Engineering，Tsinghua University，Beijing，China

A R T I C L E I N F O

Article history：

Received 30 September 2014

Accepted 17 December 2014

Available online 14 February 2015

Wide D-section cylinder

Hot wire

Phase-locked PIV

Vortex induced vibration

Lock-on

Wake structures and vortex induced vibration（VIV）of a spring-supported wide-D-section cylinder were experimentally investigated using an X-wire，a novel phase-locked particle image velocimetry（PIV），and an acceleration sensor at a low speed wind tunnel.Compared with the fixed case，the 2P（two pair）vortex mode as defined by Govardhan and Williamson（2000）rather than S（single vortex）mode exists in the wake.The velocity deficit behind the cylinder is much larger than that of fixed case.The mean drag coefficient increases from 1.42 for the fixed case to 1.64 for the vibrating case.The Reynolds stress presents even distribution and small with increased distance of X/D=-2 to X/D=-10.The power spectra density based on accelerator and hot wire data presents a highlight identical.It shows that after a strong interaction the cylinder vibration and the vortex shedding come to a stable state.The vortex shedding is totally locked on and controlled by the cylinder vibration.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

Flow induced vibration（FIV）of structures is frequently seen in industrial manufactures，such as in mechanical engineering，civil engineering，chemical engineering，marine engineering，aerospace engineering，thermal power engineering，and so on.The structures employed in those fields are initially designed to bear loadings，contain flow or provide heat transfer surface without considering fluid dynamical optimization［1］.The structures immersed in a fluid flow could be easily subject to fluid forces.Especially，fluid force fluctuation may result in vortex induced vibration（VIV）［2］，even galloping or flutter unless the structural collapses occur.The VIV easily occurs or not often depends on the shapes of structures，Reynolds number，scenario offacing flow，etc.Whetherto suppress orto utilize the VIV，orto guarantee the structuressafe，orto realize flow control，it is both essential and crucial to investigate details on the interaction between the VIV structure and the fluid flow.It motivates the present study.

There are innumerable experimental and theoretical studies on VIV of structures with simple cross section shapes.The circular cylinder is the simplest geometry and most commonly used in the industry［3］.Numerous experimental studies show that vortex shedding behind the circular cylinder causes fluctuation lift resulting in a periodical vibration，which is so-called VIV.So far，the VIV of other bluff bodies has also attracted people's interest［4，5］.The key of VIV problem exists in a strong interaction between the cylinder motion and vortex shedding［6，7］.The VIV of a cylinder is often subject to the effects of cross section shape of the cylinder，Reynolds number，Strouhal number，added mass effect，structural stiffness of the cylinder，and damping ratio［8，9］.Many semi-empirical models have been built to predict the dynamics of the VIV cylinder.Meanwhile，the two most popular models are the harmonic model and the wake oscillator model，respectively［1，10，11］.With the two models one may give a simple prediction to the VIV of a cylinder in the cross flow.

In this paper，we aim to study the flow structure and oscillation of a wide-D-section cylinder since the study is significant to engineering applications but being less concerned［12］.The flow structures around the cylinder are studied using a novel phaselocked particle image velocimetry（PIV）.The vibration of cylinder is monitored by an acceleration sensor.The velocity profiles and Reynolds stress behind the cylinder are measured by an X-wire.

The experimentwas carriedoutata low speed wind tunnelwith a square test section（0.5 m×0.5 m）of 2 m long.The wind speed can be adjusted from 0 m/s to 40 m/s.Turbulence intensity was less than 0.5%in the free stream in this experiment.A wide-D-section cylinder was horizontally supported by two springs at each end of the cylinder.The cylinder was mounted in the middle of the working section.The flat surface of the cylinder is faced to the free flow and the x-y coordinate is shown in Fig.1.The cross section of the cylinder is shown in Fig.1（b）.The blockage was about 5.5%. The mass ratio m∗was approximately 962，the structural damping ratioζwas estimated to be 0.0007 and the natural frequency fnof the spring-cylinder was 6.866 Hz.Both the natural frequency and the damping ratio were measured in the still air.The free stream velocity U0in this experiment was fixed at 4.0 m/s.The corresponding Reynolds number defined by the speed of free flow and the height of the cylinder was about 8000.

The flow structures behind the wide-D-section cylinder were captured by a standard LaVision PIV system.The smoke particle（around 2µm in diameter）generated by paraffin oil was used as trace particle.The double pulsed YAG Laser sources of a wavelength of 532 nm served as flow illumination devices in the test zone.The maximum energy outputofthe laser is about 120 mJ.The thickness of the laser sheet was about 1 mm.A single CCD camera with a resolution of 2048 pixels×2048 pixels for each image was used to capture the flow structure.The cylinder surface and the wind tunnel wall illuminated by the laser sheet were painted black to minimize the light reflection noise.The green light generated by the laser source is allowed to pass through and goes inside CCD camera by an optical filter，of which the passing wavelength is 532 nm.Velocity vector fields were calculated from the raw images by a cross-correlation algorithmbuilt in the Davis software ofthe LaV-ision system.The interrogation area was 32 pixels×32 pixels and the overlap was 50%.The weak correlation vectors were automatically removed in the post-processing.To measure the flow structures at the designated vibration phase of the spring-supported cylinder，the PIV was triggered by a dSPACE real-time control desk combined with the MATLAB/Simulink platform.Thus，a series of flow structure according with the designated vibration phase could be measured by this modified PIV technique.After phase-average calculation，a smooth and averaged flow velocity field can be obtained for arbitrary vibration phase of the cylinder.

The vibration ofthe wide-D-section cylinder was measured by a miniature B&K acceleration sensor（Delta 4516）fixed at one end of the cylinder.The signal after amplifier was collected by a NI 6521 acquisition system at a sampling frequency fsample=5 kHz，and the sampling time was about 30 s.

The velocity profile behind the wide-D-section cylinder was measured by an IFA 300 constant temperature hotwire anemometer with an X-arrangement hot film sensor Model 1246-20W（50.8µm of diameter）at X/D=-2，X/D=-5，and X/D=-10，respectively.Sixty-one points were measured along y direction at the range of Y/D=-3 to 3.Signals was offset，amplified，digitized using an 8 channel A/D board and then recorded by a computer at a sampling frequency fsample=5 kHz.The sampling time was about 26 s.The vortex shedding frequencies of the cylinder were calculated based on the power spectral density of hot wire measurements.

Instantaneous vorticity field of the fixed wide-D-section cylinder is shown in Fig.2.Vortices alternatively shed from the leading corner of the cylinder.It distinguishes from that of fixed circular cylinder［13］and square cylinder［14］.The vortices stretch muchlonger in the wake of the D-section cylinder than that of the circular or square cylinder.The vorticity is not available below the cylinder where the flow is in the shadow.

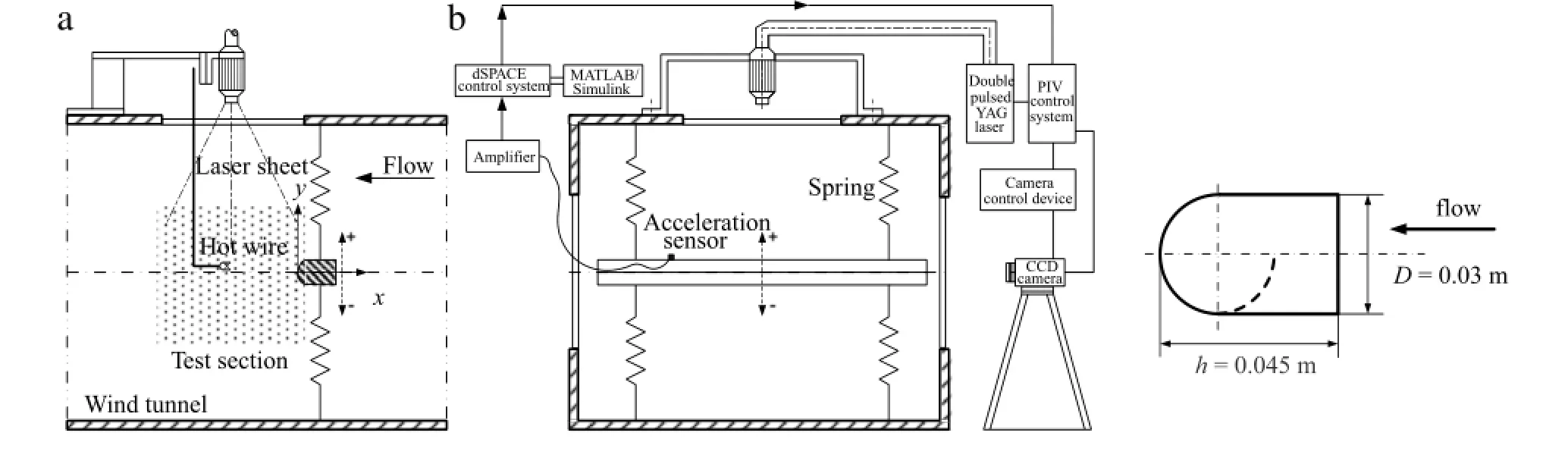
Fig.1.Experimental setup and dimensions of the wide-D section cylinder.

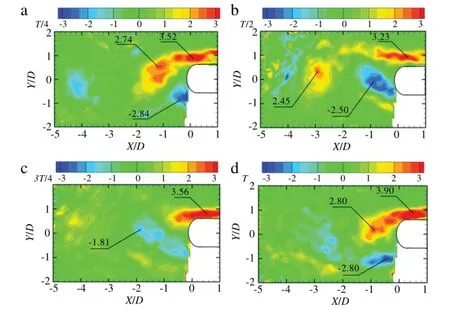
Fig.2.Normalized vorticity contours（ω∗=ωzD/U0）for the fixed wide-D cylinder，Re=8000.

Figure 3 shows the phase average results for normalized vorticity contours at designated vibration phase for the vibrating case. Each picture is the average of 300 pairs of vorticity contour which obtained using phase-locked PIV at a designated vibration phase. Figure 3（a）shows the details in vibration phases（45°of phase interval）in accordance with the vorticity contours in Fig.3（b）.Unlike the fixed case of the wide-D cylinder，the vortices form two pair vortex structure in the wake which was so-called 2P mode according to Govardhan and Williamson［20］.Figure 3（b）I-IVshow that the cylinder is moving down to the outmostposition and coming back to the balance point（Fig.3（b）IV）.Figure 3（b）IV-VI showvorticity change atthe range ofanother180°phase angle.Avortexpair including two vortices with opposite sign vorticity presents at each side of the cylinder.One of vortex in the pair forms from the natural shedding at the corner of the cylinder，another is from the induced flow because of the cylinder motion.Two vortex-pairs alternatively occur at each side of the cylinder.

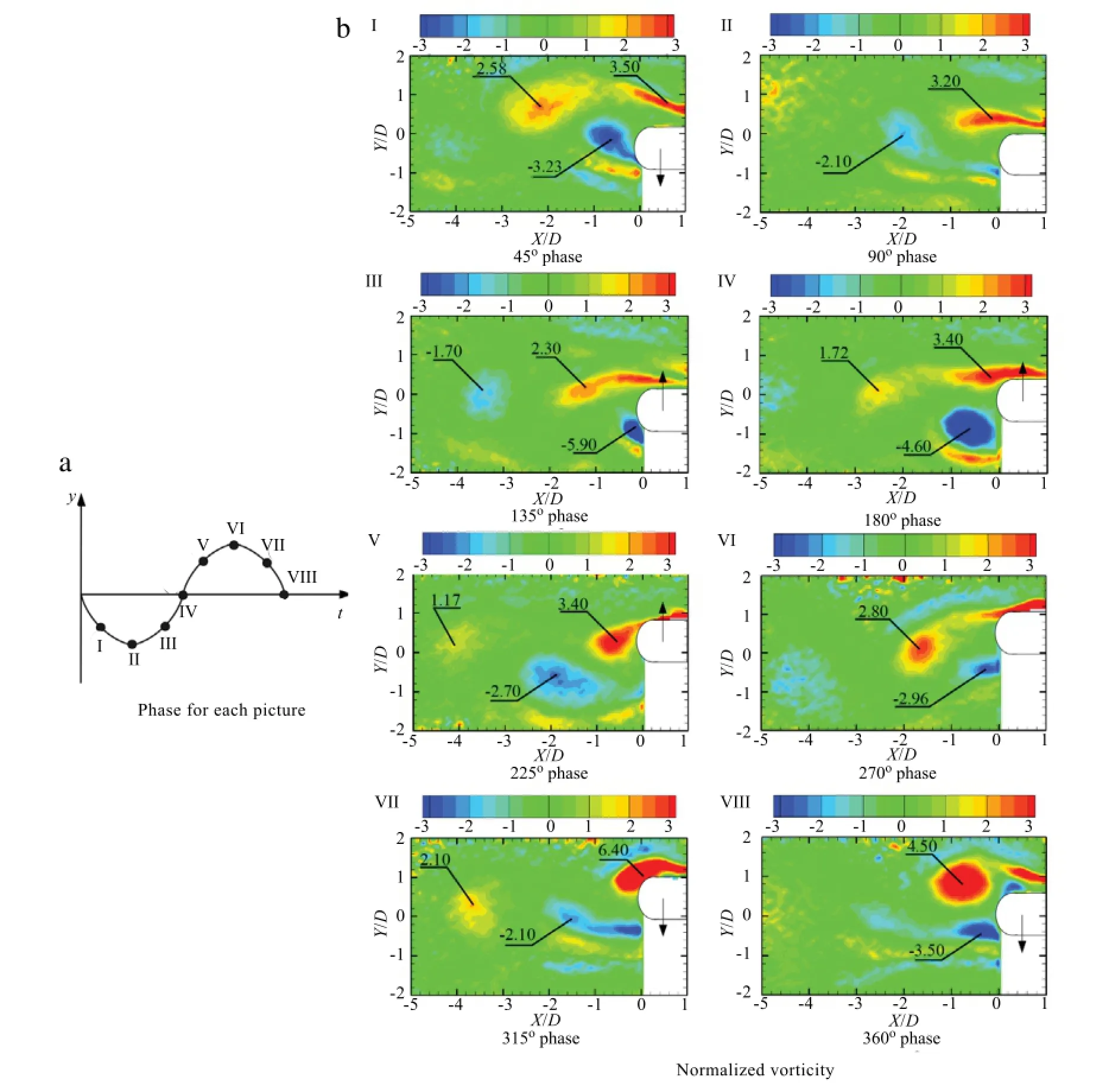
Fig.3.The normalized vorticityω∗=ωzD/U0for Re=8000.

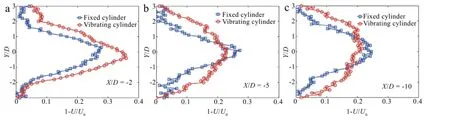
Fig.4.The mean velocity deficit at X/D=-2，X/D=-5，and X/D=-10.

The mean velocity deficit at X/D=-2，X/D=-5，and X/D=-10 obtained by an X-arrangementhotfilmisillustrated in Fig.4.The area of the deficit becomes larger as X/D increased since the wake is still developing in this range of X/D.The deficit area of vibrating case is larger than that of the fixed case.The vibrating cylinder broadened the velocity deficit in transverse direction，compared to the fixed cylinder case.

To estimate the mean drag，the algorithm［15-17］taking the Reynolds normal stress into account is adopted as Eq.（2.1）

Fig.5.profile along y direction at X/D=-2，X/D=-5，and X/D=-10.

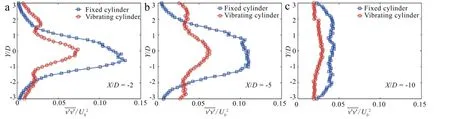
Fig.6.profile along y direction at X/D=-2，X/D=-5，and X/D=-10.

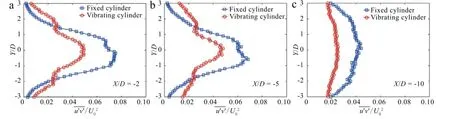
Fig.7.profile along y direction at X/D=-2，X/D=-5，and X/D=-10.

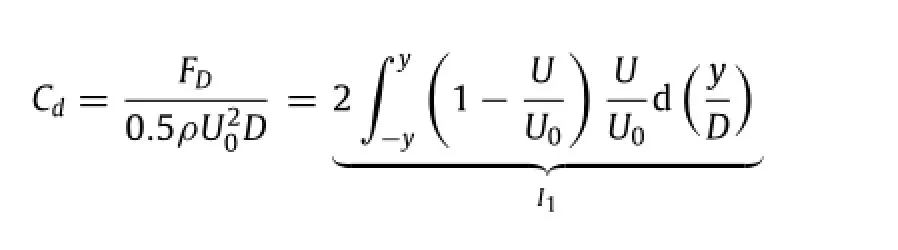
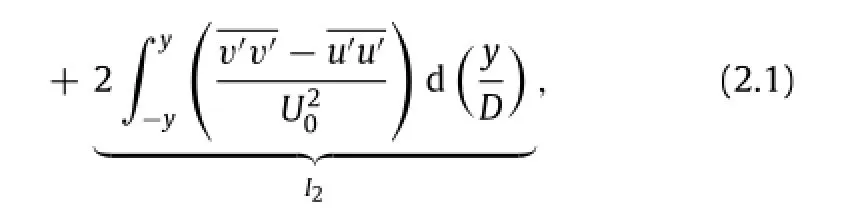
whereρis the density of the fluid，U0is the free stream velocity，and FDis the drag force.

Equation（2.1）includes two components，namely the momentum integral I1and I2，with contribution from mean velocity and Reynolds normal stress，respectively.

To measure the structural frequency of the spring-supported wide-D cylinder，acceleration of the cylinder is obtained when it is in a damped free vibration.The vibration is approximately linear. According to the measurement as shown in Fig.8，the structural damping ratioζis estimated to be 0.0007 and the structural naturalfrequency fnis 6.866 Hz，or 0.0515 normalized by D and free streamvelocity U0.As the steady VIVofthe wide-Dcylinder occurs，the acceleration becomes apparently to be periodical.The vibration frequency is identical to the natural frequency all the time.Even if the flutter occurs，the vibration amplitude increases rapidly to a new value but the vibration frequency still remains identical to the natural frequency.That is because the vortex shedding frequency is locked on the cylinder vibration.At the beginning of the cylinder vibration，the cylinder is forced to vibrate by the periodical force caused by vortex shedding（see Fig.9）.Hence，the vibration frequency is slightly higher than that of structural natural frequency of the cylinder，say 0.0878-0.0956 normalized frequency as shown as the hot wire measurement in Fig.10（notshown in acceleration data）.Power spectra density functions for different X/D fromhot wire measurement are presented in Figs.10 and 11.The fixed case is in Fig.10 and the vibrating case is in Fig.11.For the fixed case，the vortex shedding frequency（0.0956）at X/D=-2 is slightly higher than those（0.0878 and 0.0876）at X/D=-5 and-10（0.0876）.It shows that the convective velocity of the vortex is a little bit rapid that is probably caused by blockage effect near the cylinder.The convective velocity keeps nearly constant speed downstream.For the vibrating case，the vortex shedding is locked on the natural frequency of the cylinder. The dominant peak of the normalized frequency occurs at 0.0515. Meanwhile，double and triple frequencies of the value of 0.0515 also can be found in the power spectra density function.Those peaks indicate that the vortex is breaking into many small vortices downstream.

Table 1Cdof the wide-D-section cylinder.

Table 2Cdfor different cylinders.

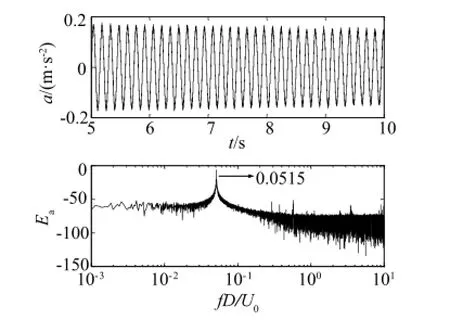
Fig.8.Acceleration and its power spectra density function for damped free vibration of the cylinder.

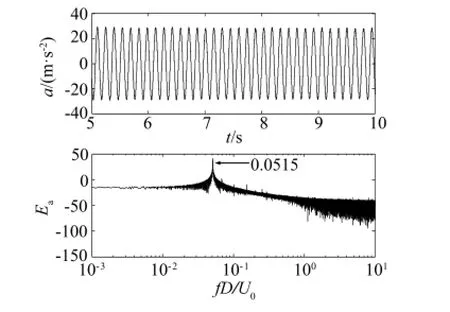
Fig.9.Acceleration and its power spectra density function for steady VIV of the cylinder.

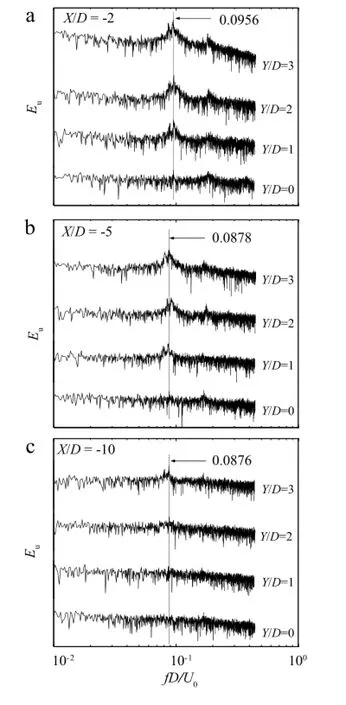
Fig.10.Power spectra density from hot wire signal for the fixed case.（a）X/D= -2；（b）X/D=-5；（c）X/D=-10.

The near wakes of a spring supported wide D-section cylinder both for fixed and vibrating cases have been studied using PIV，X-wire and an acceleration sensor.The following conclusions can be drawn.

The flow structure is influenced by the vibration of the cylinder. The wake of the vibrating cylinder presents two pair vortex structure（2P），which is different from 2S mode contained in the fixed case.The cylinder vibration results in a larger drag than that of the fixed case.In the steady VIV，the vibration frequency is identical to the structural natural frequency even if the flutter occurs.

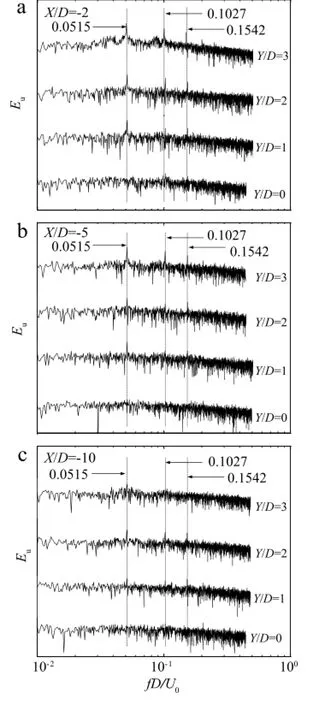
Fig.11.Power spectra density from hot wire signal for the vibrating case.（a）X/D=-2；（b）X/D=-5；（c）X/D=-10.

This work was supported by the National Natural Science Foundation of China（11472158）.

［1］R.D.Blevins，Flow-Induced Vibration，Van Nostrand Reinhold Co.，New York，1990.

［2］C.H.K.Williamson，R.Govardhan，Vortex-induced vibrations，Annu.Rev.Fluid Mech.36（2004）413-455. http://dx.doi.org/10.1146/annurev.fluid.36.050802.122128.

［3］R.D.Gabbai，H.Benaroya，An overviewofmodeling and experiments ofvortexinduced vibration of circular cylinders，J.Sound Vib.282（2005）575-616，http://dx.doi.org/10.1016/j.jsv.2004.04.017. http://www.sciencedirect.com/science/article/pii/S0022460X04004845.

［4］M.P.Païdoussis，S.J.Price，E.de Langre，Fluid-Structure Interactions:Crossflow-induced Instabilities，Cambridge University Press，Cambridge，2011，http://www.cambridge.org/us/academic/subjects/engineering/thermalfluids-engineering/fluid-structure-interactions-cross-flow-inducedinstabilities.

［5］R.M.Corless，G.V.Parkinson，A model of the combined effects of vortexinduced oscillation and galloping，J.Fluids Struct.2（1988）203-220，http://dx.doi.org/10.1016/S0889-9746（88）80008-2. http://www.sciencedirect.com/science/article/pii/S0889974688800082.

［6］P.W.Bearman，Vortex shedding from oscillating bluff bodies，Annu.Rev. Fluid Mech.16（1984）195-222.http://dx.doi.org/10.1146/annurev.fl.16. 010184.001211.http://www.annualreviews.org/doi/abs/10.1146/annurev.fl. 16.010184.001211？journalCode=fluid.

［7］R.D.Blevins，C.S.Coughran，Experimental investigation of vortex-induced vibration in one and two dimensions with variable mass，damping，and Reynolds number，J.Fluids Eng.131（2009）101-202，http://dx.doi.org/ 10.1115/1.3222904.http://fluidsengineering.asmedigitalcollection.asme.org/ article.aspx？articleid=1478300.

［8］T.Sarpkaya，A critical review of the intrinsic nature of vortex-induced vibrations，J.Fluids Struct.19（2004）389-447，http://dx.doi.org/10.1016/j.jfluidstructs.2004.02.005. http://www.sciencedirect.com/science/article/pii/S0889974604000350.

［9］M.L.Facchinetti，E.de Langre，F.Biolley，Coupling of structure and wake oscillators in vortex-induced vibrations，J.Fluids struct.19（2004）123-140，http://dx.doi.org/10.1016/j.jfluidstructs.2003.12.004. http://www.sciencedirect.com/science/article/pii/S0889974603001853.

［10］A.Farshidianfar，H.Zanganeh，A modified wake oscillator model for vortexinduced vibration ofcircular cylinders fora wide range ofmass-damping ratio，J.Fluids Struct.26（2010）430-441，http://dx.doi.org/10.1016/j.jfluidstructs.2009.11.005. http://www.sciencedirect.com/science/article/pii/S0889974610000149.

［11］N.Cagney，S.Balabani，Wake modes of a cylinder undergoing free streamwise vortex-induced vibrations，J.Fluids Struct.38（2013）127-145，http://dx.doi.org/10.1016/j.jfluidstructs.2012.12.004. http://www.sciencedirect.com/science/article/pii/S0889974612002277.

［12］P.Van Dyke，A.Laneville，Galloping of a single conductor covered with a D-section on a high-voltage overhead test line，J.Wind Eng.Ind.Aerodyn.96（2008）1141-1151，http://dx.doi.org/10.1016/j.jweia.2007.06.036. http://www.sciencedirect.com/science/article/pii/S0167610507001614.

［13］H.M.Blackburn，R.D.Henderson，A study of two-dimensional flow past an oscillating cylinder，J.Fluid Mech.385（1999）255-286，http://dx.doi.org/10.1017/S0022112099004309. http://journals.cambridge.org/action/displayAbstract？fromPage=online& aid=15051&fileId=S0022112099004309.

［14］B.W.Van Oudheusden，F.Scarano，N.P.Van Hinsberg，et al.，Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence，Exp.Fluids 39（2005）86-98，http://dx.doi.org/10.1007/s00348-005-0985-5. http://link.springer.com/article/10.1007%2Fs00348-005-0985-5.

［15］R.A.Antonia，S.Rajagopalan，Determination of drag of a circular cylinder，AIAA J.28（1990）1833-1834，http://dx.doi.org/10.2514/3.10485. http://arc.aiaa.org/doi/abs/10.2514/3.10485？journalCode=aiaaj.

［16］L.H.Feng，J.J.Wang，Synthetic jet control of separation in the flow over a circular cylinder，Exp.Fluids 53（2012）467-480，http://dx.doi.org/10.1007/s00348-012-1302-8. http://link.springer.com/article/10.1007/s00348-012-1302-8.

［17］G.S.He，N.Li，J.J.Wang，Drag reduction of square cylinders with cut-corners at the front edges，Exp.Fluids 55（2014）1-11，http://dx.doi.org/10.1007/s00348-014-1745-1. http://link.springer.com/article/10.1007%2Fs00348-014-1745-1.

［18］C.Tropea，A.L.Yarin，J.F.Foss，et al.，Springer Handbook of Experimental Fluid Mechanics，Springer-Verlag，Berlin Heidelberg，2007，pp.1125-1145，http://dx.doi.org/10.1007/978-3-540-30299-5. http://link.springer.com/referencework/10.1007%2F978-3-540-30299-5.

［19］F.M.White，Fluid Mechanics，4th edn.，McGraw-Hill，New York，2001.

［20］R.Govardhan，C.H.K.Williamson，Modes of vortex formation and frequency response of a freely vibrating cylinder，J.Fluid Mech.420（2000）85-130，http://dx.doi.org/10.1017/S0022112000001233. http://journals.cambridge.org/action/displayAbstract？fromPage=online& aid=56925&fileId=S0022112000001233.

∗Corresponding author.

E-mail address：xu_shengjin@tsinghua.edu.cn（S.Xu）.

*This article belongs to the Fluid Mechanics