一种全工况适应的全轮独立驱动车辆车速估计方法

阳贵兵，李长兵，廖自力，马晓军，刘春光

（装甲兵工程学院陆战平台全电化技术重点实验室，北京100072）

一种全工况适应的全轮独立驱动车辆车速估计方法

阳贵兵，李长兵，廖自力，马晓军，刘春光

（装甲兵工程学院陆战平台全电化技术重点实验室，北京100072）

为解决全轮独立驱动车辆车速估计难的问题，提出了一种全工况适应的车速估计方法。该方法以参数自适应卡尔曼滤波算法为基础，采用左右侧分离估计，并设计模糊控制器对滤波系数进行自适应调节，通过判断车辆的行驶工况和路面条件，设计自适应切换条件，当车轮滑转/滑移状态超过预设值，切换为纵向加速度积分估计。利用硬件在环实时仿真实验对所提出的车速估计方法的有效性和准确性进行了验证，仿真结果表明，该方法在多工况运行下具有很好的估计精度，具有普遍应用价值。

控制科学与技术；车速估计；卡尔曼滤波；全工况适应；全轮驱动

0 引言

纵向车速是车辆非常重要的状态参数之一，其估计的精度直接决定了车辆驱动防滑控制（ASR）、制动防抱死系统（ABS）以及直接横摆力矩控制（DYC）等一系列车辆稳定性控制的控制效果［1］。

全轮独立驱动车辆的纵向车速的获取，目前主要有两种方法：一是借助光学传感器或者GPS高精度测速仪［2］；二是基于普通车载传感器的估计方法［3］。第一种方法，由于涉及的成本过高，不适于量产及一般性的研究，因此第二种方法成为目前研究的主流。估计方法中，最简单的是车身加速度直接积分法，但由于积分过程中，系统噪声产生的误差不断累计，长时间积分，会导致估计结果发散，并不适应于长时间的车速估计［4］。一些学者采用了非线性车辆模型和轮胎模型，运用非线性估计算法对纵向车速进行估计［5-6］，这类方法要求的车辆和轮胎参数较多，且严重依赖参数的精确度，因此，在实际运用中受到很大的限制。除此外，文献［7］提出了一种基于卡尔曼滤波和ABS控制输入的车速估计方法，但是该方法使用的前提是有ABS介入，当车轮处于大滑转或者抱死情况下，该方法无法获得准确的估计结果。基于此，文献［1］提出了一种多方法融合的车速估计方法，但由于没有考虑多电机运行工况，因此只适合在稳态小转向、直线加速/制动工况下的车速估计。

由于全轮独立驱动车辆可完成诸如小半径滑移转向、原地中心转向等特殊转向方式，因此，其纵向车速估计方法，必须要有全工况适应性。本文以某型8轮独立驱动车辆为研究对象，在文献［1］的基础上，对卡尔曼滤波估计的轮速进行优化选取，并采用左右侧分离估计再求加权平均的方法，滤波过程中的过程噪声和量测噪声采用模糊控制器进行自适应调节，通过判断行驶工况和路面条件对自适应切换进行设计，当车轮滑转/滑移状况超过预设阀值，切换为基于车身3轴加速度传感器信号的积分估计。最后，通过多种行驶工况的硬件在环实时仿真实验，验证本文所提出的车速估计方法全工况运行下的有效性和准确性。

1 车速估计器结构及原理

图1 车速估计器结构图Fig.1 The structure of vehicle speed estimator

车速卡尔曼滤波估计（见图2），采用左右侧分离估计再进行加权平均的方法，这种方法能有效满足车辆在小半径转向、原地中心转向时，两侧轮速不同甚至一侧为正、一侧为负的情况下，对车速进行准确估计。

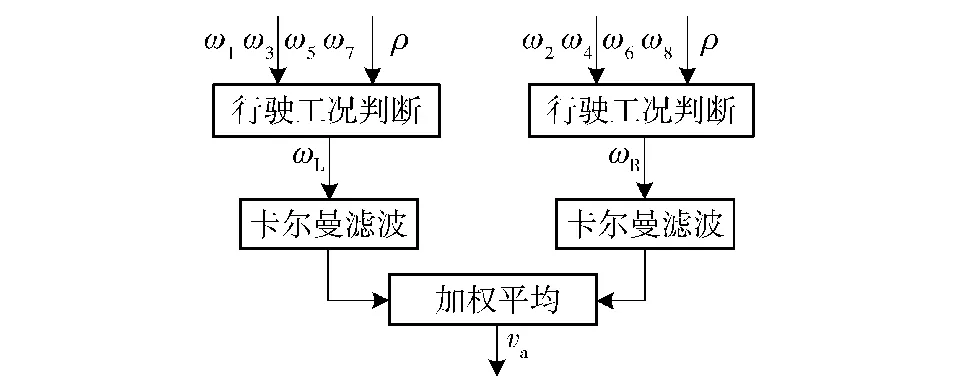
图2 车速卡尔曼滤波估计Fig.2 Kalman filter estimation

ω1、ω3、ω5、ω7表示左侧4个车轮的转速；ω2、ω4、ω6、ω8表示右侧4个车轮的转速；驾驶信号为驱动踏板信号和制动踏板信号，以左侧估计算法为例，首先根据驾驶信号判断车辆处于驱动还是制动工况，按照驱动工况取最小值，制动工况取最大值的原则，选取ω1、ω3、ω5、ω7中的最优值作为卡尔曼滤波的基准轮速ωL.

由于本文研究车辆为全轮驱动车辆，因此，车辆在低附着路面急加速、紧急制动或者其他特殊工况运行时，会出现车轮滑转或者抱死的情况，当所有车轮都发生比较大的打滑或者抱死，此时，基于轮速滤波的方法显然无法准确估计出车速，因此，本文以车轮周向加速度am与车身纵向加速度aa的差值Δa为基础，判断车轮滑转/滑移状态，通过路面附着条件μ和驾驶信号ρ设计切换条件，当Δa的值超过预设阈值，则自动切换成基于aa积分的车速估计。

2 卡尔曼滤波器设计

2.1 车速卡尔曼滤波算法

离散卡尔曼滤波算法的过程方程和量测方程分别为

式中：k为采样时刻；xk、zk分别为系统估计值和测量值；A、C分别为传递矩阵和量测矩阵；wk-1、vk分别为过程噪声和量测噪声。卡尔曼滤波过程可由下面5个式子进行描述：

式中：P为误差协方差矩阵；K为卡尔曼滤波增益；Q为过程噪声wk的方差；R为量测噪声vk的方差。

本文研究的车辆为具有双前桥转向8轮独立驱动车辆，车辆单轨运动学模型如图3所示。

图3 车辆单轨2自由度运动学模型Fig.3 2 DOF single track kinematics model of vehicle

图3中：vmi表示第i轴车轮周向速度的纵向分量；ωi为第i轴车轮的角速度；r为车轮半径，δ1、δ2分别为1、2轴转向角。

不考虑车辆高低向运动，依据线性2自由度车辆模型，车辆质心加速度与纵向车速的关系为

式中：γ为横摆角速度。

车轮周向速度的纵向分量与纵向车速的关系为

式中：Δv为由于滑转/滑移所造成的轮边速度与纵向车速的差值。

（3）式和（4）式离散化得

将（5）式中的vtγΔT定义为过程噪声wk，将Δv定义为量测噪声vk，得到卡尔曼滤波的过程方差和量测方程分别为（7）式和（8）式。

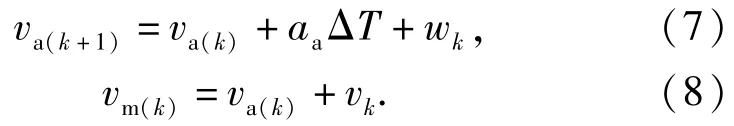
2.2 滤波器系数自适应调节

卡尔曼滤波算法的核心问题是对噪声的描述和处理，假设过程噪声wk和量测噪声vk是均值为0的高斯白噪声，其方差分别为Q和R.

由（5）式可知，过程噪声wk=vtγΔT，γ可由车身横摆角速度传感器获取，vt也可以用γ线性表示，ΔT为采样周期，在实际系统中是一个常值。因此，wkΔT的方差Q可表示为γ的二次函数Q=κγ2，其中：κ值与横向加速度at有关，at越大，κ值越大，at由加速度传感器获取。

而量测噪声是由于车轮的滑转/滑移运动所致，用Δa=|aa-am|来描述车轮的滑转/滑移状态。当Δa较小时，R也较小，反之，R值也较大。本文采用模糊规则对R值进行调节，模糊控制器的输入为Δa以及Δa的变化率Δa′，输出为R值。表1为模糊推理规则，分别以S、M、L、VL代表小、中、大和很大。图4～图6为模糊控制器输入输出的隶属度函数，图7为R映射曲面。

表1 R的模糊推理规则Tab.1 Fuzzy reasoning rule for R

图4 Δa的隶属度函数Fig.4 Membership function of Δa

3 自适应切换设计

基于纵向加速度积分的车速估计，其算法为

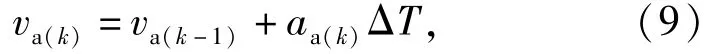
式中：va（k-1）为切换为积分估计前一个时刻卡尔曼滤波所估计的车速，以保证车速估计的连续性。

切换条件的设置，是本文研究的一个重点。本文选择Δa值作为切换条件。经过前期一系列仿真发现，当采用固定某一个Δa值作为切换阈值时，在不同附着条件的路面、不同行驶工况下，估计的效果也不同。由于Δa只是表征车辆质心加速度与轮边加速度的差，并不能表示二者速度的差，因此，会出现Δa很小而实际车速与车轮周向速度差别较大的情况。以图8所示的低附着路面加速行驶时为例，在6 s之后，8个车轮中的最小轮速与车速的增加趋势基本相同，二者的加速度值接近，Δa很小，但是速度差较大。如果在此情况下仍然以滤波方法估计车速，显然会出现较大的误差。

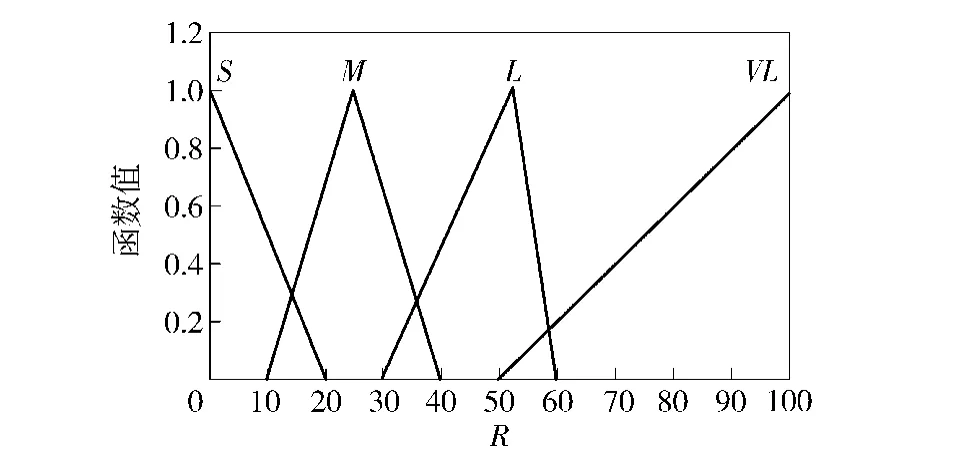
图6 R的隶属度函数Fig.6 Membership function of R

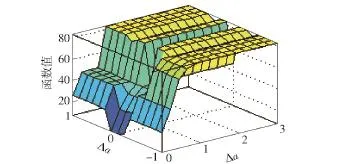
图7 R的映射图Fig.7 R mapping

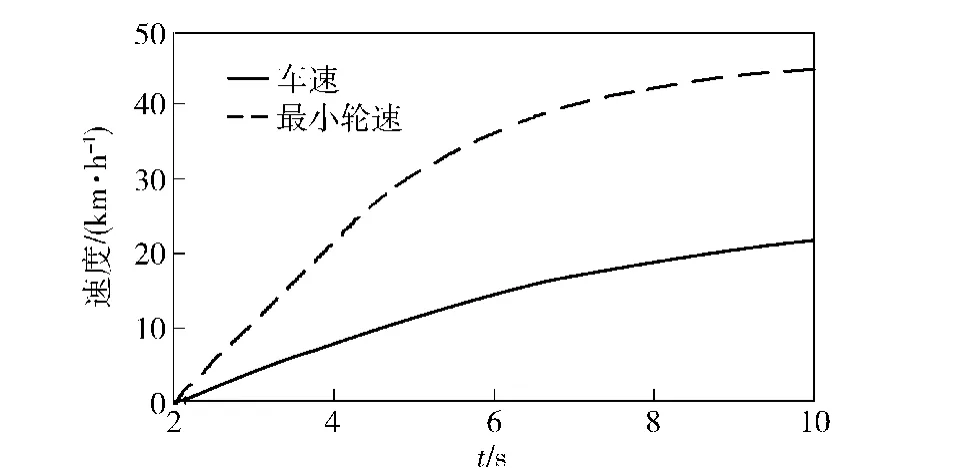
图8 车辆低附着路面加速行驶速度曲线Fig.8 Curves of accelerated running on low adhesion road

为避免上述情况的出现，本文拟采用自适应切换的方法，针对不同路面附着条件，不同行驶工况，采用不同的Δa值作为切换阈值。行驶工况主要是判断是否为急加速或紧急制动工况，可由加速/制动踏板开度ρ表示，ρ∈［-1，1］，当|ρ|＞0.8即为急加速或者紧急制动行驶。路面附着条件可由附着系数μ表示，分3种路面：高附着路面（μ＞0.8）、一般路面（0.4＜μ＜0.8）、低附着路面（μ＜0.4）.切换阈值Δa设置可由（10）式表示。

路面附着系数μ采用文献［8］的方法进行估计。

4 实验验证及分析

由于样车还未生产，本文采用基于实车中央控制器的硬件在环实时仿真实验对所提出的车速估计算法进行验证分析，硬件在环实时仿真实验是样车研制过程中必不可少的一环，可以减少样车的调试周期、降低调试成本以及安全风险，本文硬件在环实时仿真平台结构如图9所示。

该平台包括驾驶员操纵系统、控制系统、电机驱动系统以及动力学实时仿真系统4个部分，其中电机驱动系统与控制系统采用Flexray总线通信，其他系统采用CAN总线进行通信。将车速估计算法以代码形式下载到实车中央控制器，进行实时仿真实验。

为了能够客观全面验证车速估计算法，本文设计了3种路面，7种不同的行驶工况。高附着路面行驶，设计了直线加速+大半径转向、低速小半径转向、原地中心转向3种行驶工况。一般路面和低附着路面分别设计了急加速和紧急制动两种行驶工况。高附着路面行驶工况，主要是验证卡尔曼滤波算法估计的准确性。一般路面急加速和紧急制动工况主要是验证两种估计算法切换估计的准确性。低附着路面急加速和紧急制动工况主要是验证积分估计算法的准确性。仿真条件设置如下：

图9 硬件在环实时仿真平台Fig.9 Hardware-in-loop real-time simulation platform

1）高附着路面行驶工况。直线加速行驶+大半径转向，油门踏板ρ=0.8，4 s之后，方向盘打过120°转角（满程为900°）。低速小半径转向，油门踏板ρ=0.5，0.6 s后方向盘打过500°.原地中心转向，油门踏板ρ=0.5，方向盘满程。

2）一般路面行驶工况。μ=0.6.急加速行驶时，油门踏板ρ=1.0.紧急制动时，车辆从55 km/h处进行紧急制动，制动踏板ρ=-1.

3）低附着路面行驶工况。μ=0.2.急加速行驶时，油门踏板ρ=1.0.紧急制动时，从10 s开始，制动踏板ρ=-1.

仿真结果如图10～图12所示。仿真车速为Vortex软件反馈的车速，可作为参考车速。

各种行驶工况下估计车速的最大误差见表2.

表2 车速估计最大误差表Tab.2 Estimated maximum error of vehicle speed

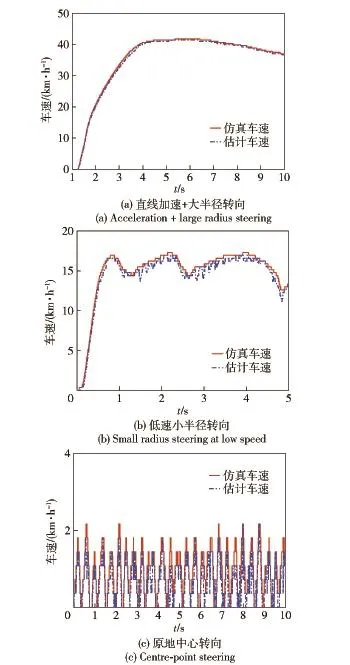
图10 高附着路面行驶Fig.10 Driving on high adhesion road

由表2可知，在所有运行工况下，估计的车速与仿真车速误差都比较小，估计精度较高，从而验证了本文所提出的车速估计算法对全工况估计的准确性。

图11 一般路面行驶Fig.11 Driving on middle adhesion road

图12 低附着路面行驶Fig.12 Driving on low adhesion road

5 结论

本文提出了一种基于轮速卡尔曼滤波与车身纵向加速度积分的车速估计方法。结合车辆运动学模型，建立了车速卡尔曼滤波估计的过程方程和量测方程，并采用模糊控制器，对滤波过程噪声的方差和量测噪声的方差进行自适应调节，设计了基于行驶工况与路面附着条件的自适应切换方法，当车轮滑转/滑移状态超过设定阀值时，切换为纵向加速度积分估计。

借助硬件在环仿真平台，设计了多种行驶工况，对本文所提出的车速估计方法的有效性和准确性进行了验证，从而为全轮独立驱动车辆提供了一种全工况适应的纵向车速估计方法。

（

）

［1］ 褚文博，李深，江青云，等.基于多信息融合的全轮独立电驱动车辆车速估计［J］.汽车工程，2011，33（11）：962-965. CHU Wen-bo，LI Shen，JIANG Qing-yun，et al.Speed estimation for all-wheel drive vehicles based on multi-information fusion［J］.Automotive Engineering，2011，33（11）：962-965.（in Chinese）

［2］ Nurhadiyatnal A，Hardjono B，Wibisono A，et al.Improved vehicle speed estimation using gaussian mixture model and hole filling algorithm［C］∥International Conference on Advanced Computer Science and Information Systems（ICACSIS）.Bali，Indonesia：IEEE，2013：451-456.

［3］ 陈慧，高博麟，徐帆.车辆质心侧偏角估计综述［J］.机械工程学报，2013，49（24）：76-94. CHEN Hui，GAO Bo-lin，XU Fan.Review on vehicle sideslip angle estimation［J］.Journal of Mechanical Engineering，2013，49（24）：76-94.（in Chinese）

［4］ 余卓平，高晓杰.车辆行驶过程中的状态估计问题综述［J］.机械工程学报，2009，45（5）：20-32. YU Zhuo-ping，GAO Xiao-jie.Review of vehiele state estimation problem under driving situation［J］.Journal of Mechanical Engineering，2009，45（5）：20-32.（in Chinese）

［5］ Shraim H，Ananou B，Fridman L，et al.Sliding mode observers for the estimation of vehicle parameters，forces and states of the center of gravity［C］∥Proceedings of the 45th Conference on Decision and Control.San Diego，CA，US：IEEE，2006：1635-1640.

［6］ 赵林辉，刘志远，陈虹.一种车辆状态滑模观测器的设计方法［J］.电机与控制学报，2009，13（4）：565-570. ZHAO Lin-hui，LIU Zhi-yuan，CHEN Hong.Design method of sliding model observer for vehicle state［J］.Electric Machines and Control，2009，13（4）：565-570.（in Chinese）

［7］ 丁能根，李丹华，余贵珍.基于卡尔曼滤波和ABS控制输入的车速估计［J］.北京航空航天大学学报，2011，37（1）：67-71. DING Neng-gen，LI Dan-hua，YU Gui-zhen.Estimation of vehicle speed based on Kalman filter and ABS control inputs［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（1）：67-71.（in Chinese）

［8］ Castro R，Araújo R E，Freitas D.Wheel slip control of EVs based on sliding mode technique with conditional integrators［J］.IEEE Transactions on Industrial Electronics，2013，60（8）：3256-3271.

Method of Vehicle Speed Estimation Adapted in All Conditions for All-wheel Independent Drive Vehicle

YANG Gui-bing，LI Chang-bing，LIAO Zi-li，MA Xiao-jun，LIU Chun-guang
（The Key Lab of All-Electric Technology of Land Warfare Platform，Academy of Armored Force Engineering，Beijing 100072，China）

A speed estimating method adapted in all conditions based on the parameter adaptive Kalman filter is established for speed estimation of the all-wheel independent drive vehicle.The left and right sides are estimated separately，and the parameters of filter are adaptively adjusted by fuzzy controller.An adaptive switching condition is designed based on drive condition and road adhesion condition.The accelerating integral is chosen when the anti-slip of the tire is higher than the preset default value.The effectiveness and accuracy of the speed estimating method are verified through hardware-in-loop real-time simulation.The simulation results show that the proposed method possesses high estimation precision under many operating condistions，and has general application value.

control science and technology；vehicle speed estimation；Kalman filter；adaption of all conditions；all-wheel drive

TJ81

A

1000-1093（2015）10-2006-06

10.3969/j.issn.1000-1093.2015.10.025

2014-12-24

军队科研项目（40402050101）

阳贵兵（1987—），男，博士研究生。E-mail：ygb1987@163.com；李长兵（1971—），男，副教授，博士生导师。E-mail：li3690@vip.sina.com