基于质量反馈的武器装备协同研制过程仿真及灵敏度分析

殷卫伟，江驹，辛君捷

(南京航空航天大学 自动化学院，江苏 南京211106)

0 引言

武器装备的研制是一个庞大而复杂的系统工程，它包括武器装备从立项到定型的整个研发过程，涉及总体和分系统等不同承研单位间的协同合作［1］。在研制过程中，常常伴随着分系统间广泛而频繁的信息交流，

为了使得多个分系统单位之间能够高效地协同合作，这就需要对其进行协调管理。所谓协同就是指协调两个或者两个以上的不同资源或者个体，协同一致地完成某一目标的过程或能力［2］。计划评审技术［3］这样传统的项目管理技术不能够很好解决航空武器装备研制工程设计中固有的耦合回路。近些年来，设计结构矩阵［4-9］(DSM)成为比较流行的一种复杂产品研制项目风险管理工具。运用设计结构矩阵DSM 既能描述任务间的并行关系，又能描述任务间的耦合关系，可以完整地描述武器装备的研制过程。

设计结构矩阵正成为一种流行的系统建模的表示和分析工具。最早Steward 提出了基于矩阵的信息流分析框架，并阐述了DSM 的理论和方法［10］。DSM 以一种简洁、可视化并且有利于分析的形式表示系统元素间的关系。其表示方式是一个具有相同行列标签的方块矩阵［5］。

如图1所示。在DSM 元素中，用1 或者X 表示对应行列元素之间有信息联系，用0 或者空格表示没有信息联系。信息总是由对应的列传输给对应的行，也就是信息是逆时针传递的。对角线以上的元素表示反馈信息，而对角线以下的元素表示前向信息。

图1 基于信息流的设计结构矩阵Fig.1 DSM based on information stream

在国内，施国强等［6］采用设计结构矩阵描述产品开发过程的串行迭代关系，仅模拟计算出项目的总工期，但显然武器装备的研制过程是一个协同并行的系统工程。杨青等［7］采用了信息输入矩阵、信息输出矩阵和返工风险矩阵，更完整地描述了任务重叠和返工迭代的过程，提出了基于顺序重叠和返工重叠的项目持续时间计算方法。但也只考虑了工期的仿真，没考虑成本也是项目管理中一个重要的风险指标，而且没有考虑多个任务重叠并行和向多个上游任务返工时的情况。张汉鹏等［8］重点考虑产品开发过程中的迭代特征，在DSM 基础上建立了返工概率矩阵和返工冲击矩阵，研究了产品开发过程中的进度风险和费用风险。赵振宇等［11］引入返工概率、返工百分比、搭接矩阵和学习曲线来描述实际设计过程的特征，但也仅仅描述了工期和费用两个参数。

为了探讨子任务的完工质量和项目的总工期和总费用的关系，本文提出质量标准向量，使得任务的返工迭代基于完工的质量综合评价系数，这样可以达到控制完工质量的效果，使得子任务的完工质量不低于质量指标，并且给出了基于质量标准向量的任务重叠时间和成本的计算方法。

本文拟以子任务的完工质量为系统输入，通过质量反馈控制使得各个子任务的质量满足要求的质量指标，运用蒙特卡罗模拟法仿真计算出项目的总工期和总费用，并根据灵敏度分析法研究各子任务完工质量的不确定性对项目的总工期和总费用的影响程度。

1 任务重叠的模型

1.1 建模方法

武器装备这样大型复杂的高新科技产品，其研制模式是基于主制造商-供应商的协同研制的过程，在保证质量的同时，企业还追求完工工期和完工成本相互权衡的最佳状态。在实际工程中，为了压缩工期，降低项目的进度风险，在传统串行方式基础上，当上游活动执行到一定程度以后，下游活动可以提前执行一定的工作量，二者在时间轴上形成交叉与重叠或部分协同并行。可以通过DSM 研制过程模型中的信息传输矩阵Tr 和信息接收矩阵Rc 来描述这种重叠并行关系［9］。

图2和图3分别是信息传输矩阵Tr 和信息接收矩阵Rc. 在信息传输矩阵中，0.8 表示任务A 完成80%工作量之后会向任务C 传递信息;在信息接收矩阵中，0.1 表示任务C 完成10%工作量之后才会接收来自任务A 的信息。

图2 信息传输矩阵TrFig.2 Information transmission matrixTr

图3 信息接收矩阵RcFig.3 Information reception matrix Rc

由此，任务A 和任务C 最理想的甘特图表示法就如图4所示。设任务A 的持续时间为tA，任务C的持续时间为tC，则t1=tA×80%，t2=tC×10%. 即任务A 执行到t1时刻时向任务C 传递信息，而任务C 执行t2时才接收来自任务A 的信息。

图4 任务重叠示意图Fig.4 Task overlapping diagram

1.2 基于顺序重叠的工期、成本计算

顺序重叠指的是上游任务与下游任务在时间轴上的部分或全部协同并行。一方面，这样的任务执行模式能够压缩项目完成工期;另一方面，通常任务并行也会产生风险，会造成返工，导致下游任务持续时间延长。如图5所示。

设任务i 的持续时间为ti，任务j 的持续时间为tj，任务j 的完工费用为cj，任务i 对任务j 的影响程度为Ri(j，i)，Tr 和Rc 矩阵分别为信息传输矩阵和信息接收矩阵，t3表示任务顺序重叠引起的时间增量，tES(j)和tEF(j)分别表示任务j 的最早开始时间和最早结束时间，cadd为任务顺序重叠引起的成本增量。忽略信息传递所需要的时间，则有如下结论:

图5 顺序重叠模型示意图Fig.5 Sequential overlapping model

1.3 基于返工重叠的工期、成本计算

返工重叠是指下游任务执行到一定程度时，向上游任务传递返工信号，造成上游任务的返工，形成了上游任务的返工部分和下游任务未完成部分(包括任务自返工的工作量)的并行，如图6所示。

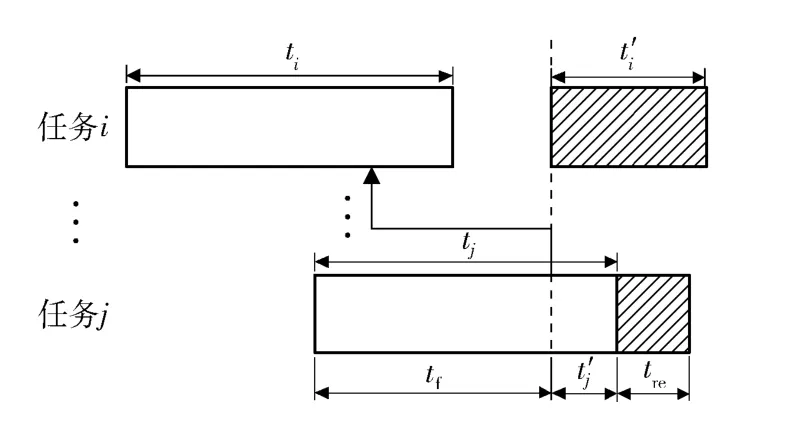
图6 返工重叠模型示意图Fig.6 Rework overlapping model

设任务i 的持续时间为ti，任务j 的持续时间为tj，任务j 对任务i 的影响程度为Ri(i，j)，任务i 的返工时间为t'i，tf表示任务在传递反馈信息前已完成的进度，任务j 的剩余时间为t'j，任务j 自返工产生的工作时间为tre，任务j 完工质量与预期质量之差为ΔQ(j)，返工重叠之后形成的时间增量为Δt，返工之后形成的成本增量为Δc. 则有如下结论:

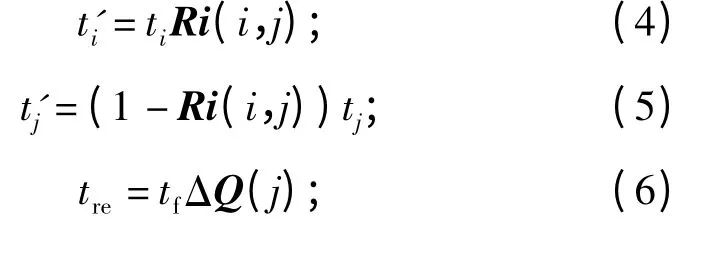
根据以上的方法可以得出整个项目的持续时间与成本。

由(2)式和(7)式可得项目的总工期

同时，由(4)式和(8)式可得项目的总成本

2 基于质量反馈的模型构建

2.1 质量反馈控制

ISO9000:2000 标准将“质量”定义为“产品、体系或过程的一组固有特性满足顾客和其他相关方要求的能力”［12］，以此衡量一项任务是否满足质量要求的参数。在自动控制系统中，被控对象的输出量，即被控量，是要求严格加以控制的物理量，它可以要求保持为某一恒定值，也可以要求按照某个给定规律运行，这就要求系统通过反馈对系统偏差进行控制［13］。把子任务的完工质量作为系统的输入，并与期望的质量指标作比较，通过任务本身的返工修正以保证其最终满足质量要求。

2.2 质量标准向量

从广义上来看，产品的广义质量是产品功能与性能的综合体现，是多个指标体系的综合评价结果。武器装备的研制过程包含多个子任务，每个任务完成后都有专门的评估小组根据子级任务的特征和性能要求进行质量综合评价。经过评估小组的综合评估之后，若满足要求的质量指标，则不需要自身返工，也不需要向上游任务传达返工信息。反之，如果此任务的完工性能不满足技术指标或客户设计要求，则对此任务进行重新修正以达到预期的质量指标。下游任务未达到质量标准，一方面，很大程度是由上游某一个或者多个任务引起，所以此时需要向上游传达信息，上游信息根据一定的概率产生返工;另一方面，由于子任务之间的耦合关系，下游任务的任务信息修改也有可能需要上游任务进行返工修改。基于这样的思路，在本节提出质量标准向量的概念。

定义1 假设某项目下有n 个任务，每个任务i预期的质量标准系数用QS(i)表示，其中i =1，2，…，n. 则这n 个分量构成了n 维的质量标准向量QS. 这里的质量标准系数用(0，1)之间的实数来量化。

武器装备的质量评价是多层次、多因素的综合评价，所以该质量标准系数QS(i)是由相应的活动实施部门和客户联合根据该活动的特性给出相应的一套评价指标体系，并依照技术人员的项目经验，综合计算得出的数据。综合评价的方法有多种选择，如模糊综合评价、主成分分析法、灰色综合评价、人工神经网络等。

3 基于质量反馈的仿真方法以及灵敏度分析研究

3.1 仿真方法研究

由于考虑仿真过程中参数不确定的情况，本文采用蒙特卡罗模拟法仿真得出结果。它的原理是以随机模拟和统计实验为手段，是一种从随机变量的概率分布中，通过随机选择数字的方法产生一种符合该随机变量概率分布特性的随机数值序列，作为输入变量序列进行特定的模拟实验、求解［14］。在工程设计研究中，蒙特卡罗模拟方法也是常用的一种方法，运用统计学原理能够得到满足一定分布函数的解。详细的仿真步骤如下:

步骤1 仿真前的准备工作。初始化数据包括n 个任务的工期、成本和完工质量的三角分布值，DSM 模型中的信息传输矩阵Tr、信息接收矩阵Rc和质量标准向量QS 等等(矩阵和向量的维数均为n)，还有一些初始化变量。n 表示项目中子任务的个数。以上关于研制过程建模的参数由各个项目小组根据经验和相关知识给出。

步骤2 设置仿真次数，并根据每个任务的工期T、成本C 和完工质量Q 的三角分布随机取样。

步骤3 判断项目的状态向量Vs = (Vs(1)，Vs(2)，…，Vs(n))中各元素是否均为2. (程序中用0 标记为还未开始实施的状态，1 表示任务正在实施的状态，2 表示任务已完成的状态。)

步骤4 遍历下游每一项任务。比如任务j(1≤j≤n)，在信息传输矩阵中，依次判断Tr(j，1)，Tr(j，2)，…，Tr(j，j -1)是否均不大于对应任务的完成进度。若满足条件，则任务j 被触发，开始执行。再结合Rc(j，1)，Rc(j，2)，…，Rc(j，j -1)，算出任务j 的最早开始时间tES(j)和最早结束时间tEF(j)，并将其状态Vs(j)置为2.

步骤5 遍历任务j 的上游任务i，1≤i≤j -1，比较tEF(i)与tES(j)的大小，若tEF(i)＞tES(j)，则说明任务i 与任务j 存在重叠，否则，两项任务之间没有重叠。根据(2)式将顺序重叠影响累加，作为当前任务j 的顺序重叠返工量。

步骤6 判断任务j 是否需要返工，即判断其模拟质量值是否小于质量标准系数QS(j). 若需要返工，则此任务先自返工，返工量=质量之差×已完成工作量。然后根据返工概率Re(k，j)，1≤k≤j -1，判断是否需要向上游任务k 传递返工影响Ri(k，j)，返工量=返工影响×上游任务已完成工作量，选出返工时间最多的任务，再比较其与下游任务j 剩余时间的大小，根据(7)式，得到返工重叠形成的时间增量。

步骤7 一次返工完成之后，继续判断对下游任务执行二次返工，返工量=质量之差×返工影响×下游任务已完成工作量。

步骤8 返回步骤3，继续判断任务状态向量Vs(n)，即所有任务是否都已完成。

步骤9 仿真完成之后，可以得到每次模拟整个项目的工期和成本，并可以对结果进行统计分析。

3.2 基于质量指标信息的灵敏度分析

灵敏度分析是指定性或定量地研究模型输入的不确定性对模型输出不确定性的影响［15］。一直以来，这都是分析人员研究的热点课题。本文采用适用于不确定环境下的基于蒙特卡罗模拟的灵敏度分析方法。

在工程实际中，为了保证规定的质量要求或者追求优质的质量，项目中任务的完工质量影响着项目的总工期和总成本。本文为了探索各个任务质量的变化对项目的总工期和总成本的影响程度，用灵敏度系数来表示。一般地，灵敏度系数用Si表示:

式中:Si表示因变量对自变量i 的灵敏度系数;Δ 表示因变量的相对变化幅度;δi表示自变量的相对变化幅度［16］。在本文中，自变量为每个任务的完工质量的模拟值，取值为［0，1］中的一个实数;因变量为项目的总工期或者总成本。

对于航空武器装备这样的大型研制项目，为了更好地对过程质量进行控制和管理，应该合理分配资源，有重点地管理过程活动。通过灵敏度分析，可以确定在研制过程中对项目总工期和总成本最敏感的任务工序。这样有利于管理者对资源的分配和对过程的管控。

4 案例实现与分析

4.1 数据收集以及模型构建

现以某军用飞机预研设计过程为例，包含客户需求分析、初步结构设计、发动机设计与评估、飞行动力学分析、外形设计、气动弹性设计、空气动力学设计、姿态控制系统设计、机体内部负载分析、机体结构设计、电气组件设计、机体装配工艺规划、重量与惯性分析和项目计划安排，共14 项任务，分别用字母A ～N 标记。为了描述此预研设计过程，根据项目的历史经验，由专家组给出数据，建立有如下模型，见表1. 考虑到研制过程的不确定性，其中假设任务工期、成本和质量均满足三角分布，3 个特征点分别是最乐观的、最可能的和最悲观的情况。

图7和图8用信息传输矩阵和信息接收矩阵来描述子任务之间的并行关系，如Tr(3，1)=0.8 表示任务A 完成80%工作量之后向任务B 传递信息;Rc(3，2)=0.1 则表示任务C 完成10%工作量之后会接收来自任务A 的信息。

表2中的每个数据均表示相应子任务的质量标准系数，以此作为子任务需要返工的依据。若当前任务的模拟质量低于质量标准系数，则其本身需要自返工以达到质量指标要求，然后再判断是否向与当前任务有信息联系的上游任务返工。

图9和图10 用返工概率矩阵和返工影响矩阵来描述子任务之间不确定的返工事件，如Re(3，4)=0.8，表示任务D 在不满足质量标准的情况下，有80%的概率向任务C 传递返工信息;下三角元素Re(3，2)=0.7，表示任务B 返工完成之后，继续向下游任务C 传递信息，任务C 二次返工的概率是70%;Ri(3，4)=0.6 则表示若任务C 发生返工，需要返工已完成工作量的60%.

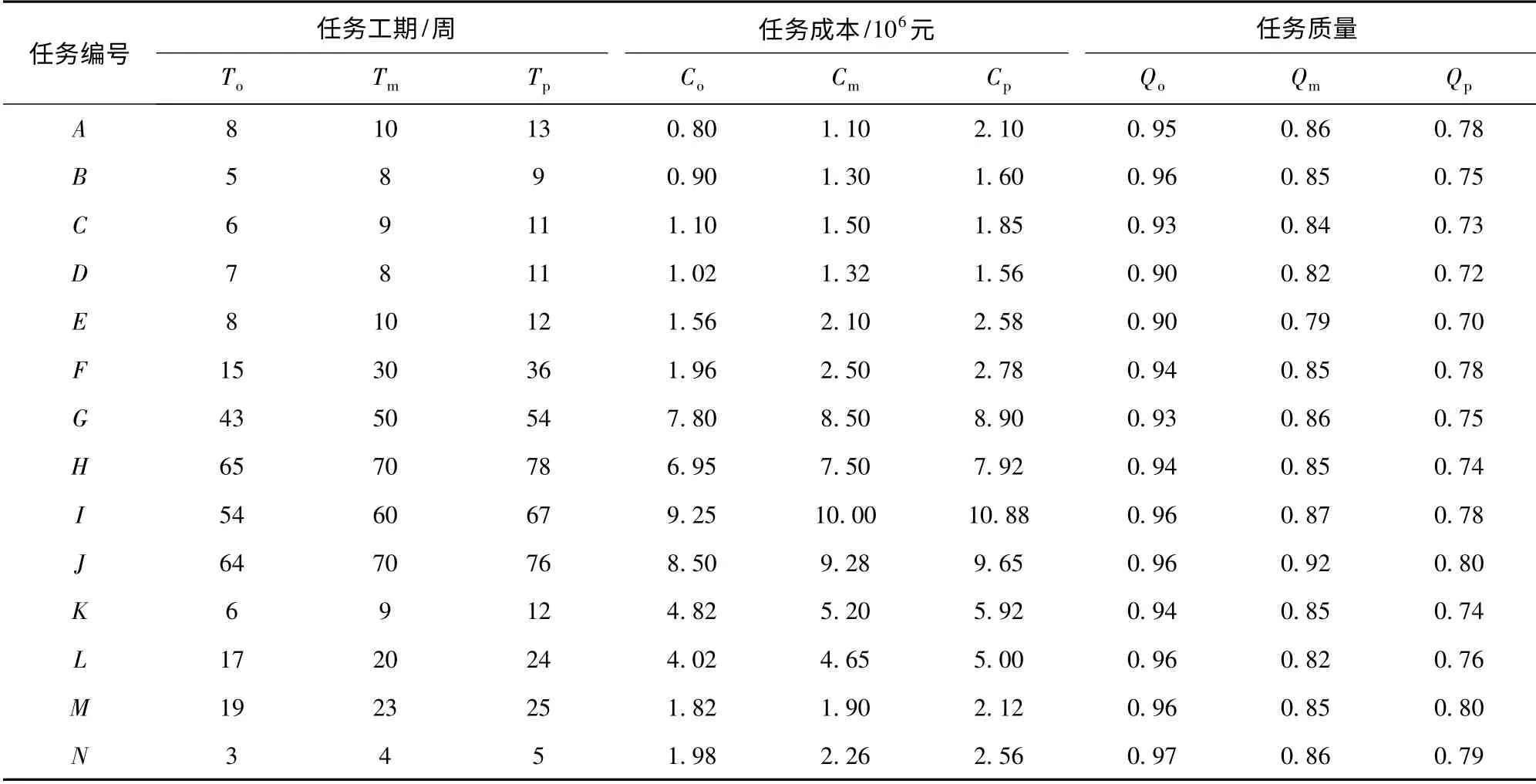
表1 某军用飞机预研设计过程的工期、成本和质量的三角评价值Tab.1 The triangle values of time，cost and quality in the predesign process of a military aircraft

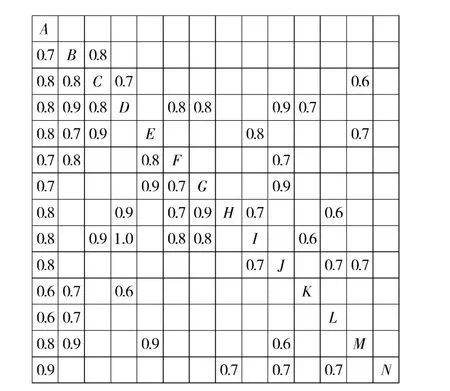
图7 信息传输矩阵TrFig.7 Information transmission matrix Tr

图8 信息接收矩阵RcFig.8 Information reception matrix Rc

表2 质量标准向量QSTab.2 Quality standard vector

4.2 仿真结果分析

经过蒙特卡罗模拟仿真后，可以得到每次仿真得到的总工期和总成本。由于只看数据，根本不能看出仿真反映的情况，所以需要对数据进行统计分析，根据结果可以画出工期和成本的概率密度分布图，可以很清楚地看出工期和成本的分布情况。图11 为完工时间的概率密度分布图和累计概率分布图。图12 为完工费用的概率密度分布图和累计概率分布图。最终得到总工期的期望是184.10 周，总成本的期望是130.23 ×106元。

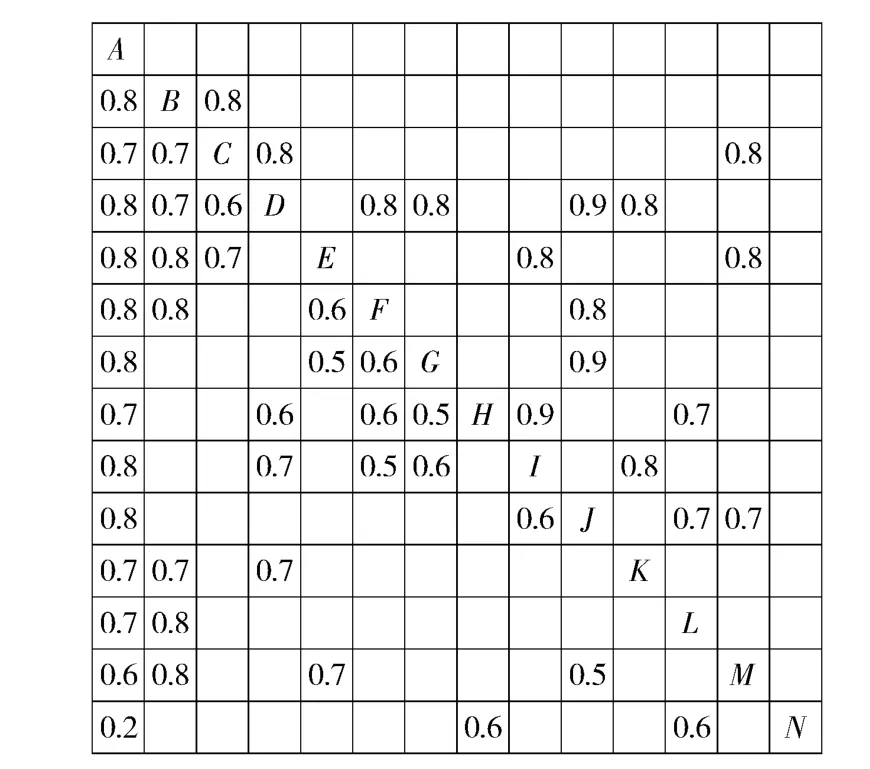
图9 返工概率矩阵ReFig.9 Rework probabilities matrix Re

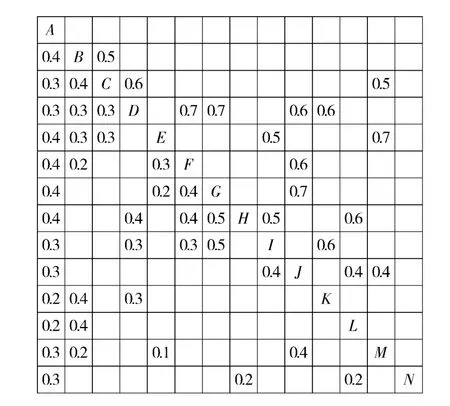
图10 返工影响矩阵RiFig.10 Rework impacts matrix Ri

观察概率密度的分布图，可以很清晰地看出项目总工期和总成本分布疏密情况，项目完工时间最有可能的时间是170 ～190 周，完工费用最有可能是130 ×106～135 ×106元. 观察累计概率分布图，可以看出项目在某一个工期目标或成本目标内完成的概率，如在图11(b)中，完工时间小于186 周的概率为63.33%.

4.3 灵敏度分析

由于本文采用基于蒙特卡罗模拟的灵敏度分析方法，数据在一定的范围内产生波动。为了避免自变量与因变量之间相关关系的误会，而且本文主要是探索每个任务对整个项目工期和成本风险的影响程度，所以本文一律采用灵敏度的绝对值来表示每个任务的波动幅度。

图11 完工时间的分布情况Fig.11 The distribution of completion time

本文将每项任务的完工质量分别变化为±20%、±10%和±5%等6 个值，得到每项任务在不同的质量变化率下引起项目总工期和总成本的变化幅度。图13 和图14 分别是各任务对项目总工期和总成本的灵敏系数。

观察图13 可以看出:

1)从纵向上可以发现，子任务质量的提高，没有质量降低时的灵敏度明显，说明项目总工期的压缩空间不是很大，反而质量下降会对项目进度风险造成更大的影响。

2)从横向上可以发现，“机体结构设计”和“重量与惯性分析”两项任务的灵敏度比较突出，其完工质量对项目总工期的影响程度较高，所以在项目管理中应重点加强对这两项任务的管理与监督，增加资源的调度以及与这两任务小组的信息交流，提高两项任务的完工质量，这样可减少进度风险。

同样从图14 中也能得出类似的结论。

图12 完工费用的分布情况Fig.12 The distribution of completion cost

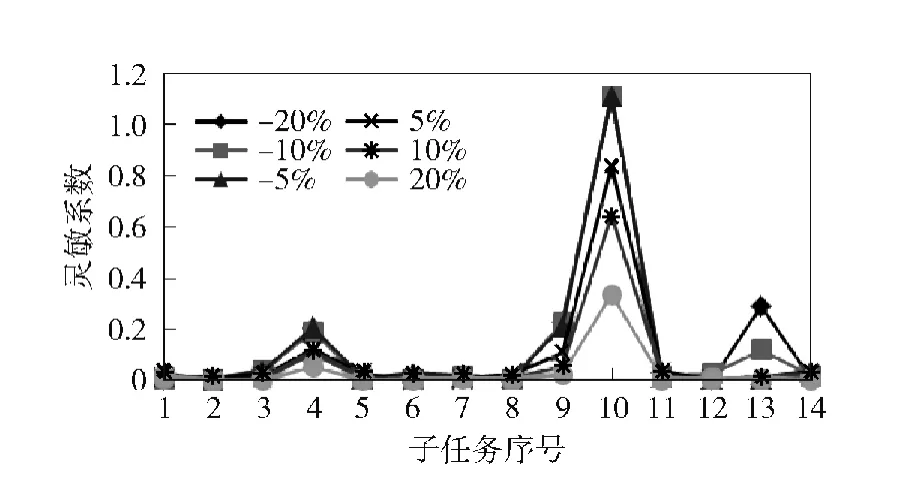
图13 各子任务对项目总工期的灵敏度对比示意图Fig.13 The sensitivities of sub-tasks during project duration

5 结论

本文提出一种基于质量反馈的DSM 模型，将项目的工期风险和成本风险与子任务的完工质量联系在一起探索，更加贴近工程实际。然后使用质量标准向量和任务重叠模型共同描述武器装备研制过程，给出了蒙特卡罗模拟仿真过程。最后，对仿真结果进行统计分析和灵敏度分析，识别对项目进度风险和费用风险影响程度最大的任务。实验结果表明，预研过程的14 项子任务中，“机体结构设计”任务的灵敏度最高，这为决策者提供了一定的参考价值，提醒项目管理者可以通过协调资源的分配以有重点地控制项目风险。

图14 各子任务对项目总成本的灵敏度对比示意图Fig.14 The sensitivities of sub-tasks for the total project cost

References)

［1］李金林. 武器装备研制项目风险管理［M］. 哈尔滨:哈尔滨工程大学出版社，2010.LI Jin-lin. Weapon equipment development project risk management［M］.Harbin:Harbin Engineering University Press，2010.(in Chinese)

［2］许晓燕，赵武，姜迎春，等. 基于过程的协同技术在产品质量管理中的应用［J］. 工业工程，2007，10(2):97 -101.XU Xiao-yan，Zhao Wu，JIANG Ying-chun，et al. Application of cooperation technology based on process in product quality management［J］. Industrial Engineering Journal，2007，10(2):97 -101.(in Chinese)

［3］巴延廷. 基于PERT 的工程进度风险分析研究［D］. 大连:大连理工大学，2010.BA Ting-ting. The research on Project risk analysis based on PERT［D］. Dalian:Dalian University of Technology，2010. (in Chinese)

［4］Shekar B，Venkataram R，Satish B M. Managing complexity in aircraft design using design structure matrix［J］. Concurrent Engineering，2011:1063293X11426461.

［5］Browning T R. Applying the design structure matrix to system decomposition and integration problems:a review and new directions［J］.IEEE Transactions on Engineering Management，2001，48(3):292 -306.

［6］施国强，李伯虎，柴旭东. 基于设计结构矩阵的复杂产品开发项目规划模型［J］. 计算机集成制造系统，2008，13(11):2105 -2109.SHI Guo-qiang，LI Bo-hu，CHAI Xu-dong. DSM-based modeling of project scheduling for complex product development［J］. Computer Integrated Manufacturing Systems，2008，13(11):2105 -2109.(in Chinese)

［7］杨青，黄建美. 基于活动重叠的DSM 项目时间计算及排序优化［J］.系统工程理论与实践，2011，31(3):496 -504.YANG Qing，HUANG Jian-mei. Project calculation and optimization based on DSM activities overlapping［J］. System Engineering-Theory ＆ Practice，2011，31(3):496 -504.(in Chinese)

［8］张汉鹏，邱菀华. 基于DSM 优化的产品开发两因素风险建模及仿真［J］. 北京航空航天大学学报，2007，33(5):627-630.ZHANG Han-peng，QIU Wan-hua. Product development two-factor risk model and simulation based on DSM［J］. Journal of Beijing University of Aeronautics and Astronautics，2007，33(5):627 -630.(in Chinese)

［9］辛君捷. 基于设计结构矩阵的航空武器装备研制过程风险分析与智能优化［D］. 南京:南京航空航天大学，2013.XIN Jun-jie. Research of risk analysis and intelligent optimizing of air-weapon developing process based on design structure matrix［D］.Nanjing:Nanjing University of Aeronautics and Astronautics，2013.(in Chinese)

［10］Steward D V. The design structure system-a method for managing the design of complex systems［J］. IEEE transactions on Engineering Management，1981，28(3):71 -74.

［11］赵振宇，游维扬，吕乾雷. 基于遗传算法和蒙特卡洛模拟的并行工程设计工序优化［J］. 土木工程学报，2009(2):139 -144.ZHAO Zhen-yu，YOU Wei-yang，LYU Qian-lei. Design process sequencing optimization of concurrent engineering projects based on genetic algorithm and Monte Carlo simulation ［J］. China Civil Engineering Journal，2009(2):139 -144.(in Chinese)

［12］郑唯唯. 过程质量控制智能化体系与方法研究［D］. 西安:西北工业大学，2006.ZHENG Wei-wei. Reseach on the system and methods of intelligent process quality control［D］. Xi＇an:Northwestern Polytechnical University，2006.(in Chinese)

［13］胡寿松. 自动控制原理［M］. 修订本. 北京:科学出版社，2008.HU Shou-song. Automatic control theory［M］. Revised ed.Beijing:Science Press，2008.(in Chinese)

［14］宋淳江. 基于设计结构矩阵的复杂产品系统伙伴选择研究［D］.杭州:浙江大学，2011.SONG Chun-jiang. A study based on design structure matrix for partners selection of complex［D］. Hangzhou:Zhengjiang University，2011.(in Chinese)

［15］陆凌云. 基于仿真实验的灵敏度分析方法及工具研究［D］.哈尔滨:哈尔滨工业大学，2013.LU Ling-yun. Research on sensitivity analysis methods and tool based on simulation experients［D］. Harbin:Harbin Institute of Technology，2013.(in Chinese)

［16］徐哲，贾子君. 基于图示评审技术多反馈仿真的武器装备技术风险评估［J］. 计算机集成制造系统，2010，16(3):636 -642.XU Zhe，Jia Zi-jun. Assessment of technical risk for weapon system development project based on GERT simulation including multi-branch feedback［J］. Computer Integrated Manufacturing Systems，2010，16(3):636 -642.(in Chinese)