脉冲爆轰发动机爆轰噪声场区域划分及其数值模拟

黄孝龙，许桂阳，翁春生，李宁

(南京理工大学 瞬态物理国家重点实验室，江苏 南京210094)

0 引言

脉冲爆轰发动机(PDE)是一种新型发动机，与传统发动机相比，具有燃烧效率高，结构简单等优点。但是，与其他发动机一样，PDE 在工作过程中会产生较大噪声，对相关工作人员和设备的正常工作会产生较大影响。因此，对其噪声的研究，具有重要意义。

Boesch 等［1］测量了PDE 管外轴线上不同距离处的爆轰噪声，并通过理想冲击波理论，较为准确地预测出了爆轰波的爆轰噪声峰值和频谱变化。Glaser 等［2］对PDE 出口不同距离、不同方位角处的噪声进行了测量，发现:随着出口距离的增加，声压峰值逐渐减小;并且冲击波传播速度在出爆轰管口很短的距离内，迅速衰减为声速;声压辐射曲线，呈现出明显的指向性;并通过定义参考半径，将爆轰发动机声场分为强冲击波区和弱冲击波区，分别给出了PDE 爆轰噪声峰值在参考半径内外的变化规律，与实验测量所得噪声峰值变化规律一致。He 等［3］对PDE 的爆轰噪声做了初步的数值模拟研究，计算了爆轰管内和管外不同位置的声压级，并通过傅里叶转换初步得到了爆轰噪声声压级的估计值，峰值声压常出现在频率为330 Hz 范围。Eerden 等［4］在求解点爆炸产生的冲击波由近场强非线性区向远场线性区转变的过渡过程中，提出划分计算区域的思想，采用不同的方法求解不同区域的控制方程，并与采用一种计算方法得到的结果对比，得出区域划分可以更好地模拟点爆炸声场传播特性的结论。

PDE 爆轰噪声与点爆炸相似，都会产生高强度的冲击波。在此前研究的基础上，本文尝试将划分计算区域思想应用到PDE 爆轰噪声的研究中。根据冲击波强弱，将PDE 爆轰噪声场划分为3 个区域，并采用相应的计算方法对PDE 爆轰噪声场的传播过程进行数值模拟，得到爆轰噪声的分布规律。

1 PDE 爆轰噪声场的分区及计算方法

PDE 爆轰噪声主要由冲击波噪声和喷流噪声组成，即爆轰波从爆轰管口逸出并退化为冲击波引起的冲击噪声以及紧随其后的高温高压燃气射流引起的射流噪声。为了便于计算与分析，爆轰噪声由近场到远场的传播过程划分为3 个区域，如图1所示:第1 区域为近场的强非线性区，主要由冲击波和高速射流引起的极强非线性噪声组成;第2 个区域为近场与远场之间的过渡区，即声波由强非线性声波向线性声波过渡的区域;第3 个区域为远场线性声波区。

根据文献［5］中超压在6.0×103～1.96×104Pa 可作为冲击波与冲击声波过渡边界的结论，结合PDE爆轰噪声实验测量结果与数值计算结果，划定PDE爆轰噪声由近场向远场传播的3 个区域界线，如图1所示。超压≥9 100 Pa，为强非线性区。1 000 Pa≤超压＜9 100 Pa，为弱非线性区。超压＜1 000 Pa 作为线性区。当PDE 噪声传播到线性区时，控制方程为线性声波方程，采用抛物线方程(PE)法对其进行求解。由于线性方程的求解比较简单，本文对线性区不再介绍，着重对前两部分进行研究。

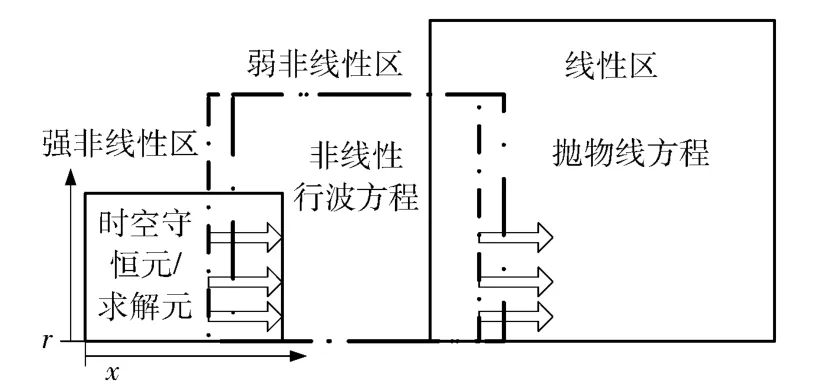
图1 爆轰产生的冲击波由近场向远场传播过程数值计算的区域划分Fig.1 Schematic diagram of the propagation of a shock wave from a source of detonation to the far field

1.1 强非线性区控制方程及计算方法

不考虑流体微团间的热传导和热辐射等耗散效应，考虑粘性影响下的PDE 外流场轴对称控制方程［6-7］为

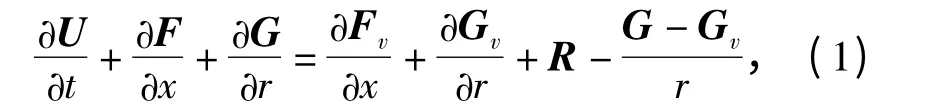
强非线性区域内PDE 噪声具有极强的非线性，采用时空守恒元/求解元(CE/SE)方法求解轴对称纳维-斯托克斯方程。CE/SE 方法是近年来求解强间断的一种新的数值方法。它最初由美国国家航空航天局科学家Chang［8］提出，该方法在构造思想上与其它传统的数值方法有所不同，它将空间与时间统一对待，从守恒律积分方程出发，设立守恒元和求解元，使其计算格式在局部和全部计算区域内严格保证物理意义上的守恒。CE/SE 方法可以准确捕捉非线性区的重要特征:强间断性。

PDE 外流场计算区域如图2所示。轴向和径向计算总网格数为1 200 ×1 200，再增加网格数量对计算结果影响极小。ABFG 所围区域为PDE 管，BCDEFG 所围成的区域为外流场计算区域。FG 为PDE 管管壁，BG 为PDE 管管口，AB、BC 段采用轴对称边界条件，CD、DE、EF 段采用非反射自由边界，AF、FG 段采用固壁反射边界条件，BG 采用入口边界条件，将脉冲爆轰发动机管内流场中爆轰管出口参数作为外流场计算的入口参数。

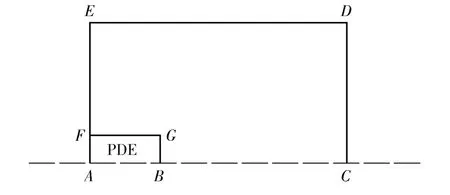
图2 强非线性区计算区域示意图Fig.2 Schematic diagram of computational domain

1.2 弱非线性区控制方程的推导及计算方法

第2 个区域为弱非线性区，是由强冲击波向线性声波的转变过程，这个区域的声压变化采用非线性行波方程(NPE)进行描述，NPE 方程由McDonald和Kuperman 首先提出，该模型被最初广泛应用于预测高强度冲击波在水中向远场线性区的传播过程，近几年也被成功的应用于预测弱非线性声波在空气中的传播，Piacsek 等［9］将NPE 方程用于计算飞行器在高空突破音速时产生的音爆向地面传播的过程。NPE 方程是基于弱非线性声波扰动的单一方程，同时考虑了波传播过程中的折射和非线性等因素，且其计算区域是以当地声速向x 正方向移动的，可以很好捕捉计算区域有限振幅的变化。

轴对称柱坐标系下的NPE 方程［10］为

将p'关于ρ'做2 阶展开可得

定义无量纲压强的Q =p'/ρ0c20，由(3)式可知，Q=R+O(ρ'2)，若取1 阶近似，则二者相等，因此，在理想流体中，可以将NPE 方程演变为关于Q 的方程。

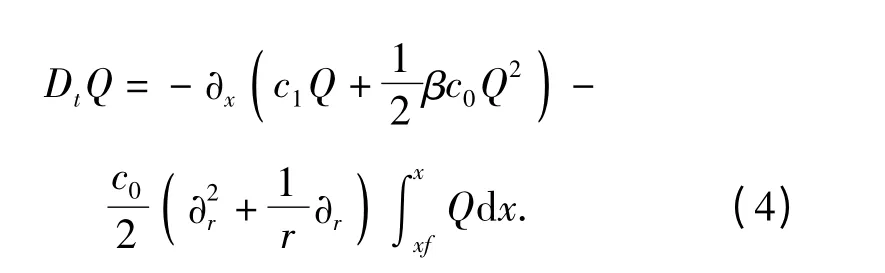
本文采用时间算子分裂格式对NPE 方程进行求解，即对(4)式右边两项采取不同格式进行求解。其中第1 项为非线性项，采用2 阶迎风通量校正格式(FCT);对于右边第2 项，即衍射项，采用Crank-Nicholson 方法进行离散求解，对于其中的积分项，采用梯形积分法进行求解。

对于NPE 算法计算区域，同样采用轴对称方程建立模型及矩形网格划分方法。由于NPE 方程建立时进行了小角度的近似，因此从声源点开始，计算区域与对称轴所成的夹角不能大于10°. 如图1中标注区域所示，NPE 计算的区域采用动网格法，计算区域的移动速度和当地声速一致，随时间的积累向前移动。NPE 算法程序的计算网格的长度的选取中，x 代表对称轴方向，r 代表径向方向，轴向上网格长度dx =0.25 cm，径向上dr =0.125 cm. 选取340 m/s 为当地音速。对于计算区域的上和右边界，均采用p =0，对称轴上采用轴对称边界条件:

2 计算结果及分析

2.1 强非线性区计算结果及分析

图3 PDE 管外的压力云图Fig.3 Pressure nephogram outside PDE

图3为爆轰发动机出口处，不同时刻，CS/SE 方法计算得到的爆轰管外的压力云图。其中图3(a)、图3(b)和图3(c)分别为0.138 ms、1.324 ms、4.014 ms时刻的爆轰管外的压力云图。从图3(a)中可以看出，爆轰波离开出口以后，迅速退化为无化学反应的“弓形”激波，在激波掠过区域，形成高压区。“弓形”激波具有明显的指向性，在轴向位置上压力最高，随着角度的增大，压力下降。同时，管内喷射的高压爆轰产物在出口附近形成球状膨胀波向四周膨胀，由于过渡膨胀，在膨胀波后产生负压区。由图3(b)可以看出，随着时间的推移，激波沿轴向和径向方向上继续传播，最先形成的激波逐渐衰减，激波后面的膨胀波继续向外传播，并由于燃烧产物是以喷流方式向外喷出，与管外静止空气边界层形成的强烈的湍流脉动，导致涡系的产生，在x =0.35 m 上方，存在一明显涡系。随着时间的推移，涡系沿轴向传播。当t=4.014 ms 时，退化的激波传播到1.8 m，涡系传播到0.8 m 处。

2.2 弱非线性区计算结果及分析

图4为在4.014 ms 时，管外对称轴上的声压曲线。此时，冲击波的波阵面距离爆轰管口1.8 m，峰值为9 100 Pa，声压级达到173.16 dB，根据分区判断标准，爆轰噪声开始进入弱非线性区。如图1中所示，强非线性区与弱非线性区的计算区域存在交汇区，利用交汇区内第1 区的计算结果，作为第2 区计算的初始值。由于除了第1 个完整波形之外的曲线上升与下降，均为涡系所导致，而涡系会随传播距离的增加而迅速衰减，因此计算中只取第1 个完整波形。取强非线性区计算结果中，x 方向上1.2 ～2.0 m，r 方向上0 ～0.8 m 区域作为NPE 计算区域的初始值，如图5所示。因为NPE 方程是关于声压的单一方程，因此，将强非线性区计算结果减去大气压的值作为下一步计算的初值。

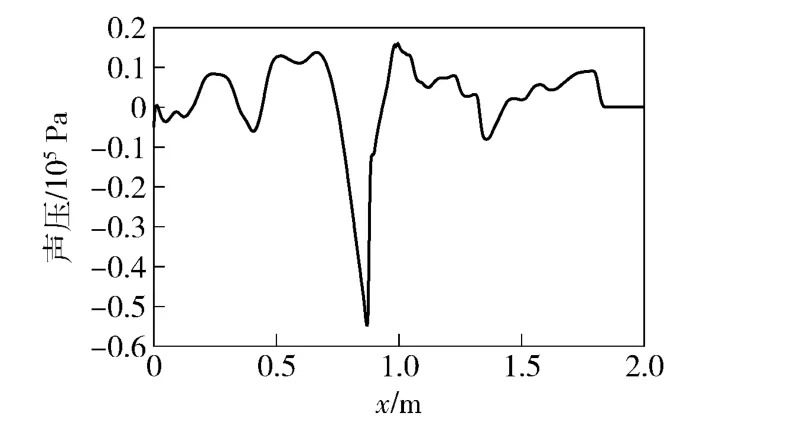
图4 轴线上的声压变化曲线Fig.4 Curve of on-axis sound pressure

图6、图7和图8分别为扰动传播到距离爆轰发动机管口2.3 m、5.8 m 和10.0 m 位置处，由NPE方程计算得到的声压云图。由于声波的衍射作用，声波在轴向和径向上传播。随着能量的扩散，压力扰动的区域越来越大。径向上的压力扰动由最开始时的0.8 m 处传播到3.4 m 处，轴向上的压力扰动由1.8 m 处传播到10.0 m 处，径向上的压力扰动传播速度明显较慢。这是因为PDE 爆轰噪声具有明显的指向性，能量主要集中在轴向上，因此在轴向上的传播速度快于径向上的传播速度。由于传播过程中，声波的能量扩散衰减，声压峰值也从9 100 Pa(173.16 dB)，衰减为6950 Pa(170.82 dB)、2 645 Pa(162.43 dB)和1 515 Pa(157.58 dB)，且在能量较高区域，衰减速度较快。衰减速度最快时可达3 756 Pa/m(33 dB/m). 然后，衰减速度逐渐减慢，在接近线性区时，衰减速度最小为198.18 Pa/m(1.02 dB/m).

3 计算结果与实验结果的对比及分析

图5 弱非线性区的初值压力云图和轴线上的声压曲线图Fig.5 Pressure nephogram and curve of initial sound pressure in weak nonlinear region

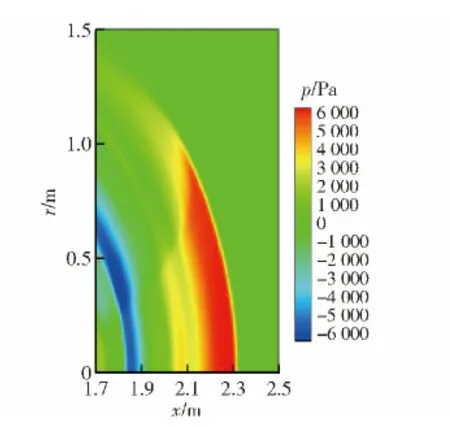
图6 波振面到达2.3 m 时的压力云图Fig.6 The pressure nephogram at 2.3 m

为了验证PDE 爆轰噪声场计算结果的准确性，对相应距离处PDE 管外的爆轰噪声声压进行了测量。所用PDE 试验系统主要包括PDE、供气系统、供油系统、点火控制系统和测试系统等。以93 号汽油为燃料，空气为氧化剂，脉冲爆轰发动机爆轰管直径为80 mm，工作频率为10 Hz，传感器布置于距离管口0.4 m、0.8 m、1.2 m 、1.6 m、2.4 m、3.0 m、5.0 m 和10.0 m 处，测试得到的噪声电信号通过信号调理器处理后由同步数据采集系统采集，采样率为500 kS/s.

声压级的表达式为

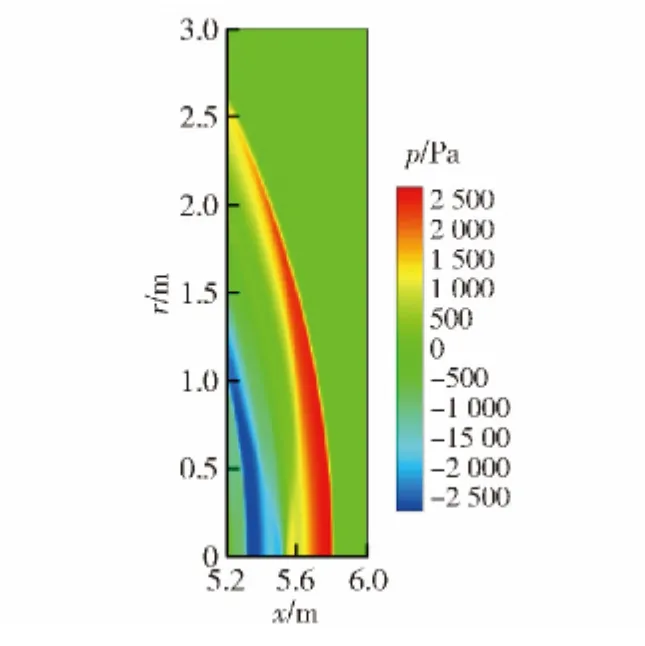
图7 波振面到达5.8 m 时的压力云图Fig.7 The pressure nephogram at 5.8 m

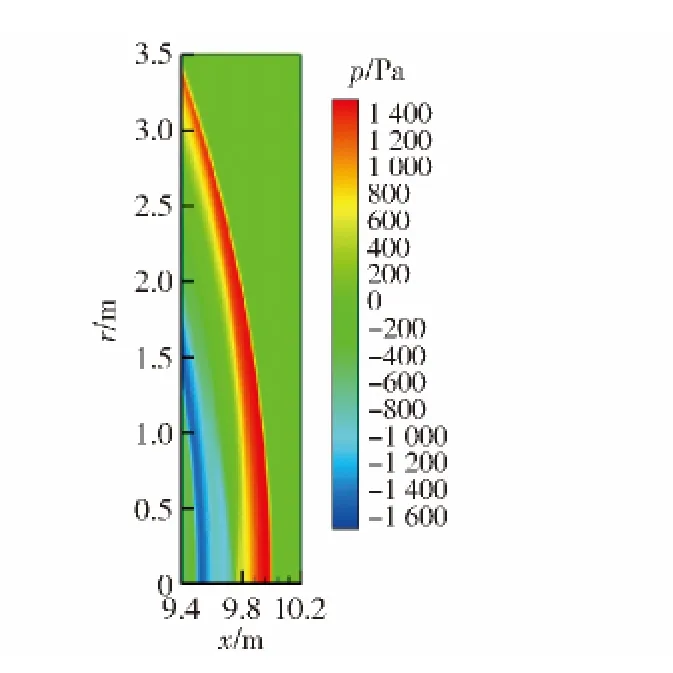
图8 波振面到达10.0 m 时的压力云图Fig.8 The pressure nephogram at 10.0 m

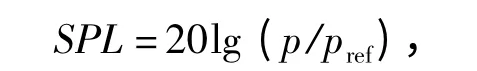
式中:SPL 为声压级(dB);p 为声压(Pa);pref=2 ×10-5Pa，为基准声压。

分别取强非线性区和弱非线性区内对称轴上不同位置处的观测点计算得到的压力峰值，连同实验测量所得数据，绘制峰值压力随轴向距离x 变化的曲线，如图9所示。在强非线性区压力峰值迅速下降，衰减速度较快。这是由于在此区域，冲击噪声相比射流噪声要大很多，但由于冲击噪声在大幅值时衰减较快，导致该区域的压力峰值迅速衰减。到1.6 m 处，随着冲击噪声的迅速衰减，喷流噪声占据主导地位，其衰减速度相对较慢。但是，当脱离燃气喷流核心区时，由于湍流脉动效应的减小，喷流噪声较快衰减。此时小振幅冲击噪声的峰值衰减速度相对较慢。在2.4 m 处，冲击噪声占据主要地位，进入弱非线性区，由于小振幅冲击噪声的衰减速度减慢，因此之后的噪声峰值的衰减速度也相对较慢。

PDE 近场爆轰噪声峰值ppeak与轴向距离x 的倒数满足一定的变化规律，计算公式［2］为

图9 PDE 爆轰噪声声压衰减曲线Fig.9 Curves of PDE detonation noise amplitudes on axis

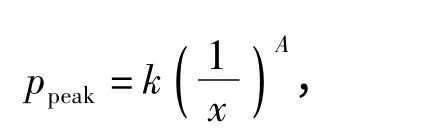
式中:k 为衰减系数，A 为非线性系数。当在非线性区时，1 ＜A≤3. 非线性程度越强，A 的取值越接近3;非线性程度弱，A 的值接近1. 利用数值计算和实验测量所得声压级绘制随轴向距离x 的变化规律，如图10 所示。其中x 采用对数坐标，A =1.0 直线为以第2 区最后1 个点为参考点、A 的值取1.0 绘制的曲线。可以看出，在最开始的时刻，衰减速度很快，此时A=2.1. 随着轴向距离的增加，速度减慢。但在第2 区中，衰减速度逐渐变缓，其中到x =10 m处最后一个点时，A =1.02，此时声压级的衰减规律已经很接近线性区的衰减规律。

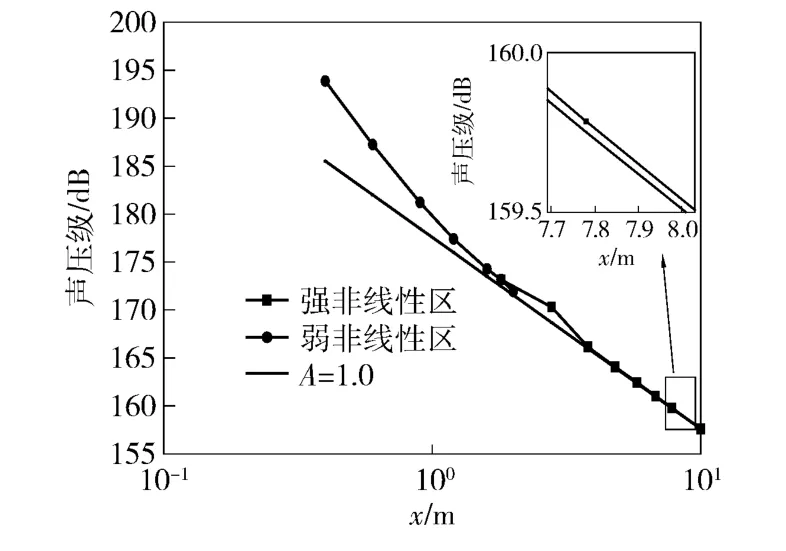
图10 衰减规律拟合曲线Fig.10 Fitting curves of attenuation law

4 结论

将PDE 爆轰噪声场进行分区求解，可以有效的模拟出脉冲爆轰发动机爆轰噪声的传播特性，避免了单一方法计算的不准确性，对PDE 爆轰噪声场的传播特性的研究具有重要的参考价值。并得出以下结论:

1)以超压9 100 Pa 作为强非线性区和弱非线性区的判断标准是合理的，可以有效避免CE/SE 方法计算误差所产生的衰减速度较快现象。

2)爆轰噪声峰值声压级，在出口处迅速衰减。随着轴向距离的增加，衰减速度逐渐放缓。在强非线性区，衰减速度最大值可达33 dB/m. 在弱非线性区，最小衰减速度为1.02 dB/m. 非常接近线性区的衰减速度。

References)

［1］Boesch H E，Reiff C G，Benwell B T.Modification of the acoustic spectrum of detonation tube shock waves by timed multiple-pulse addition，ARL-TR-2203［R］. America:Army Research Laboratory Report，2000.

［2］Glaser A J，Caldwell N，Gutmark E.A fundamental study on the acoustic behavior of pulse detonation engines［C］∥45th AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada，US:AIAA，2007.

［3］He X，Karagozian A R . Performance and noise characteristics of pulse detonation engines［C］∥42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada，US:AIAA，2004.

［4］Eerden F V，Védy E. Propagation of shock waves from source to receiver［J］.Noise Control Engineering，2005，53(3):87 -93.

［5］王秉义.枪炮噪声与爆炸声的特性和防治［M］. 北京:国防工业出版社，2001:31 -32.WANG Bing-yi. Gun muzzle noise ＆ explosive sound-Character，Protection and control［M］. Beijing:National Defence Industry Press，2001:31 -32.(in Chinese)

［6］王杰，翁春生.脉冲爆轰发动机冲击波外流场数值模拟［J］.火炮发射与控制学报，2009，30(3):53 -56.WANG Jie，WENG Chun-sheng. Numerical simulation shock wave exteral flow of pulse detonation engine［J］. Journal of Gun Launch＆ Control，2009，30(3):53 -56.(in Chinese)

［7］王研艳，翁春生. 尾喷管构型对多循环两相脉冲爆轰发动机流场及性能影响［J］.航空动力学报，2013，28(10):66 -69.WANG Yan-yan，WENG Chun-sheng. Effects of nozzle on flow field and performance of multi-cycle two-phase pulse detonation engines［J］. Journal of Aerospace Power，2013，28(10):66 -69. (in Chinese)

［8］Chang S C. The method of space-time conser vation element and solution element-a new approach for solving the navier-stokes and euler equations［J］. Journal of Computational Physics，1995，119(2):295 -324.

［9］Piacsek A A，Locey L L，Sparrow V W. Time-domain modeling of atmospheric turbulence effects on sonic boom propagation［C］∥14th AIAA/CEAS Aeroacoustics Conference. Vancouver，British Columbia，Canada:AIAA，2008.

［10］Piacsek A A，Plotkin K J. Application of nonlinear progressivewave equation to sonic boom transition focus［C］∥51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Grapevine，Texas，US:AIAA，2013.