固液两相流离心泵内颗粒运动规律的数值研究*

夏 密，李 昳，李凤琴

(浙江理工大学 浙江省流体传输技术重点实验室，浙江 杭州 310018)

0 引言

固液两相离心泵输送的对象是水和固体颗粒的混合物，通常广泛用于冶金、化工、土建和环保等行业。由于密度、直径和浓度等固相参数的不同，复杂的泵内流道几何形状以及叶轮高速的旋转等因素，加上固相和液相两相之间的耦合作用、固相与固相之间的耦合作用、固体颗粒与壁面之间的碰撞反弹这些现象的存在，导致离心泵内部两相流动的研究极为复杂。

目前，国内外关于固液两相流内部流动特性的数值计算和实验研究很多，大多应用Mixture 多相流模型对不同的两相流泵内部固液两相流动机理、外特性性能进行数值模拟和实验研究［1-7］。也有一些学者应用离散相模型对两相流泵内部流动特性进行了相关的数值计算，研究了颗粒运动以及流道过流部件的磨损性能［8-11］。求解带有粒子存在的流动，最直观和容易理解的就是离散相模型，而离散相模型假定颗粒相非常稀疏，因此可以忽略颗粒与颗粒之间的相互作用、颗粒体积分数对连续相的影响，一般要求颗粒的体积分数小于10%～12%，颗粒质量载荷可以大于10%～12%。

本研究中所加颗粒浓度小于10%，fluent 中离散相模型可以考虑到离散相的惯性力、重力、曳力等多种力的作用，Fluent 软件的一个用户接口—用户自定义函数(UDF)中离散相模型具备可以自定义除了重力及阻力以外的自他体积力的宏函数，故考虑颗粒体积效应，颗粒所受Basset 力可以通过UDF 引入计算。

因此，本研究应用离散相模型针对不同固相参数固液两相流动工况，对离心泵内部颗粒运动轨迹、固相速度分布规律以及颗粒雷诺数在流道内的分布规律进行数值分析，为研究颗粒运动规律提供可靠的数值研究方法。

1 几何模型及求解方法

1.1 计算模型和网格参数

本研究的计算模型选用M196-100 叶片式离心泵，流量Q=100 m3·h－1，扬程H=20 m，转速n=2 900 r/min。

整个流体计算区域由进口延伸段、叶轮区域、蜗壳和蜗壳出口延伸段四部分组成，其中叶轮区域和蜗壳区域采用了四面体非结构化网格划分，进口延伸段和蜗壳延伸段采用了结构化的六面体网格划分。

经过网格无关性验证结果如图1 所示。

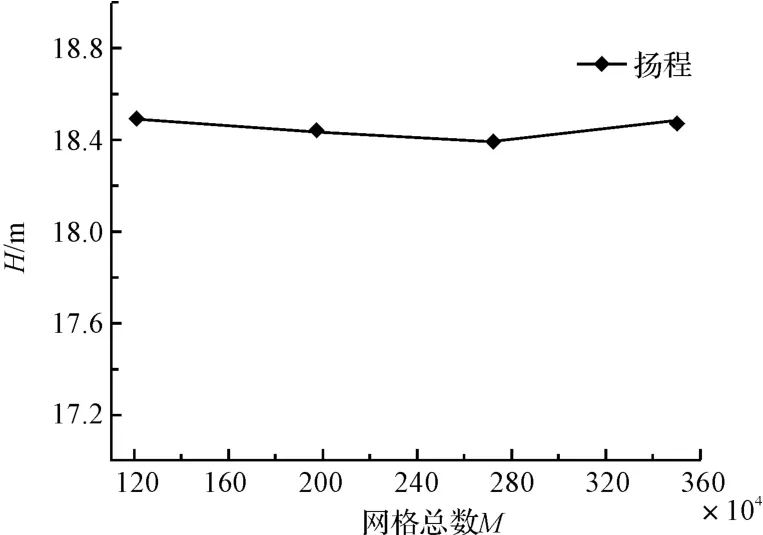
图1 网格无关性验证

当计算域的网格总数为1.21×106时，网格数量的增加对计算结果精度影响不大，故计算中模型网格总数为1.21×106。

计算域内流体是不可压缩流体，本研究设置进口处的边界条件为速度入口，进口速度可以由设计工况体积流量计算得出。假定流体到达出口边界时流动已充分发展，本研究设置自由出流为出口处边界条件。叶轮和蜗壳的壁面都采用无滑移固壁边界条件。粒子在进出口处都采用逃逸边界条件，在各过流部件内表面的边界条件设置为reflect，且为弹性碰撞。

1.2 固液两相流控制方程

液相是连续相，为不可压缩液态水，其控制方程为连续方程和动量方程［12］。

固相颗粒为离散相，固体颗粒的运动轨迹可通过对拉格朗日坐标下颗粒作用力微分方程积分来求解。颗粒在固液流场中主要受重力、绕流阻力、附加质量力、压强梯度力、Basset 力、Saffman 升力、Magnus 力等作用力。一般情况下只考虑重力和阻力。经过量级分析，当固相直径超过0.5 mm 时，已经不能忽略Basset力的作用［13］。本研究在计算时所加颗粒直径大于1 mm，故采用了UDF 引入Basset 力进行计算。

颗粒运动方程为:

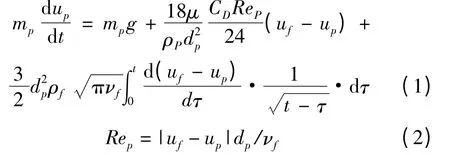
式中:mp，ρp，dp，up—颗粒的质量、密度、直径和速度;CD—阻力系数;μ—流体动力粘度;ρf，uf—流体密度和速度;ReP—颗粒雷诺数;|uf－up|—两相间滑移速度;νf—流体运动粘度。

2 计算结果分析

2.1 清水工况结果分析

不同流量工况下，离心泵水力扬程、效率数值计算结果与实验结果曲线对比图如图2 所示。

由图2 可以看出，计算值与实验值［14］变化基本一致，扬程随流量的增加会下降，效率随流量的增加先升高后降低。

笔者设计工况点Q=100 m3/h 时，实验的扬程为18.8 m，效率为82.5%，数值计算结果的扬程为18.5 m，效率为85.01%，扬程、效率相对误差率分别是1.6%和3.04%，都在允许的误差范围内，这说明了本研究中采用的数值计算方法可靠。

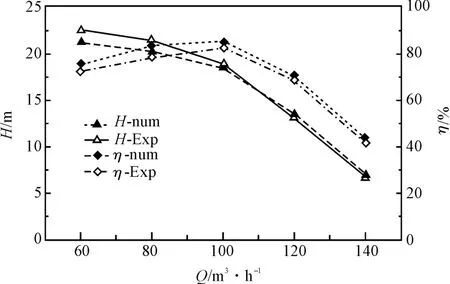
图2 实验和数值计算水力性能曲线对比

2.2 离散相模型计算结果及分析

计算固相颗粒属性如下:

颗粒直径分别为1 mm，1.75 mm，2.5 mm;密度为1 550 kg·m－3;固相体积分数分别为1%，5%，10%。

设计工况下，固相体积分数Cv=10%时，颗粒在整个流道内的运动轨迹随直径变化图如图3 所示。

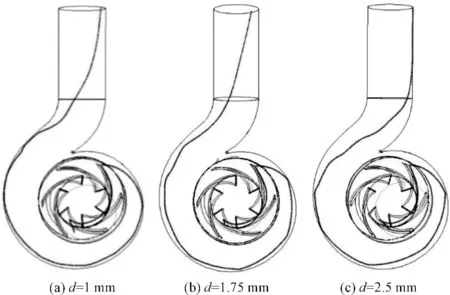
图3 颗粒运动轨迹随直径变化图(Cv=10%)

从图3 中可以看出，颗粒在叶轮流道内的轨迹变化基本一致，直径的变化对颗粒运动轨迹的影响不明显。颗粒从进口处入射随液体运动进入流道，到达叶片进口处附近时与叶片发生了碰撞，碰撞位置在压力面尾端处。颗粒进入叶轮流道后，由于叶片的旋转运动导致颗粒运动过程中会受到离心力和圆周力作用，与叶片工作面头部会发生第二次碰撞，而后进入蜗壳流道与蜗壳壁面发生碰撞。直径变化对蜗壳内部颗粒运动轨迹的影响较为明显，当颗粒的直径比较小时，颗粒与蜗壳流道的碰撞的次数会比较多，但是碰撞次数会随着直径的增大逐渐减少。这主要是由于直径达到一定量级时候，重力以及其他惯性力对颗粒作用影响增大，使颗粒随液相运动的跟随性也会变差。

设计工况下，颗粒直径d=2.5 mm 时，不同固相体积浓度工况下，颗粒在整个流道内的运动轨迹图如图4 所示。

图4 颗粒运动轨迹随浓度变化图(d=2.5 mm)

从图4 中可知，颗粒浓度变化对颗粒运动轨迹有一定影响。在叶轮流道内的颗粒运动轨迹随浓度变化与随直径变化的规律基本一致，颗粒从叶轮进口到叶轮出口，与叶片的工作面发生了两次碰撞。当颗粒浓度较小时，颗粒沿蜗壳流道的外缘壁面运动，与其碰撞次数会比较多，而浓度的增加会导致颗粒的运动轨迹逐渐偏离蜗壳外缘壁面，使其与蜗壳碰撞的次数减少。

设计工况下，Cv为10%时，固相速度在流道内的分布规律随直径变化图如图5 所示。

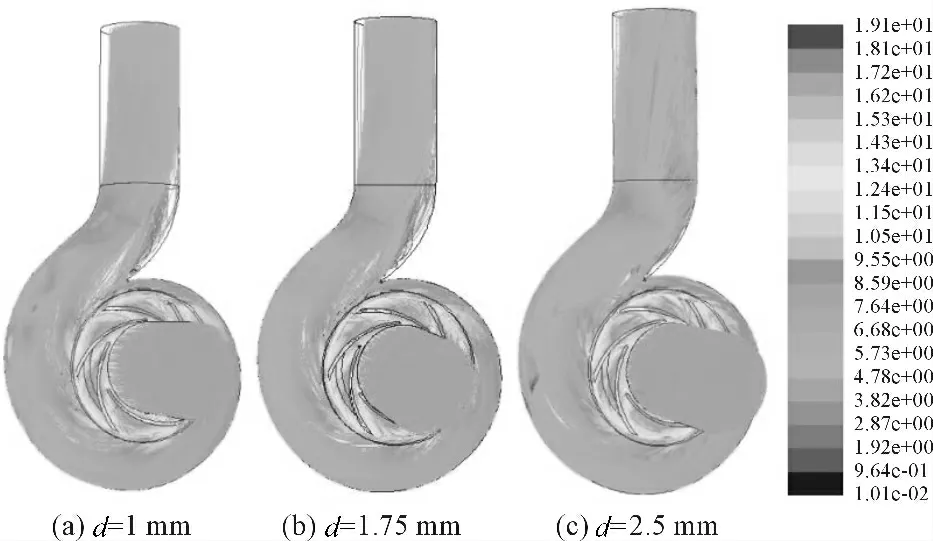
图5 固相速度随直径变化图(单位m·s －1)(Cv=10%)

不同直径下的固相速度变化规律大致相同。叶轮流道内，叶轮进口处速度较小，从叶轮进口到叶轮出口，固相速度逐渐变大。蜗壳流道内，从叶轮出口到蜗壳出口，固相速度是呈减小趋势的。蜗壳出口处，因为回流的出现，导致固相的速度逐渐降低。隔舌附近由于隔舌的阻碍作用使颗粒速度减小。随着直径增大，叶轮内固相速度基本变化不大，但蜗壳流道到出口处，固相速度稍有减少。

设计工况下，颗粒直径为2.5 mm 时，固相速度在流道内的分布规律随浓度变化图如图6 所示。

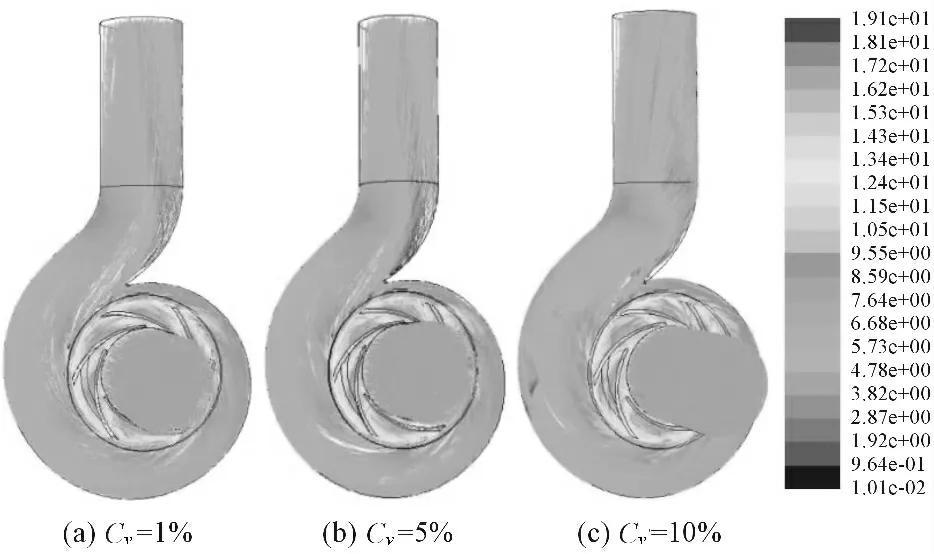
图6 颗粒运动轨迹随浓度变化图(d=2.5 mm)

浓度不同时的固相速度变化规律基本一致。叶轮流道内，叶轮进口处速度较小，从叶轮进口到叶轮出口，固相速度逐渐变大，叶轮进口处速度最小为2.87 m·s－1，出口处最大为17.3 m·s－1。蜗壳流道内，从叶轮出口到蜗壳出口，固相速度逐渐减小。隔舌附近速度最小，最小值为0.166 m·s－1。浓度的变化对固相速度的影响不大，蜗壳出口处，浓度较小时，靠近隔舌这一侧的速度值比较小，而浓度较大时，这一侧的速度值比较大。这主要是由于直径不变，因为离散相模型的粒子添加量整体较小，随液相运动的跟随性大体相同，颗粒在流场中所受力大小也基本相同，导致固相颗粒运动的速度分布也具备大致相同的规律。

设计工况时，不同直径工况下颗粒雷诺数在流道内的分布如图7 所示。

图7 颗粒雷诺数随直径变化图(Cv=10%)

由颗粒雷诺数公式可以推断，随着直径的增大，颗粒雷诺数增大，而图6(a)、6(b)、6(c)中3 幅图的变化趋势证明了该结果。颗粒直径较小时，从进口延伸段到出口，固相和液相两相间的滑移速度比较小，叶轮流道处由于叶轮的旋转运动对颗粒运动的影响，导致此处两相分离较大，故此处的颗粒雷诺数比较大。当d=1 mm 时，颗粒雷诺数最小为0.014 4。直径较大时，叶轮流道到蜗壳流道两相分离比较严重，相间滑移速度大，故直径较大时，叶轮和蜗壳流道的颗粒雷诺数也比较大。当d=2.5 mm 时，颗粒雷诺数最大为42 775.29。

设计工况下，d=2.5 mm 时流道内颗粒雷诺数随浓度的变化图如图8 所示。

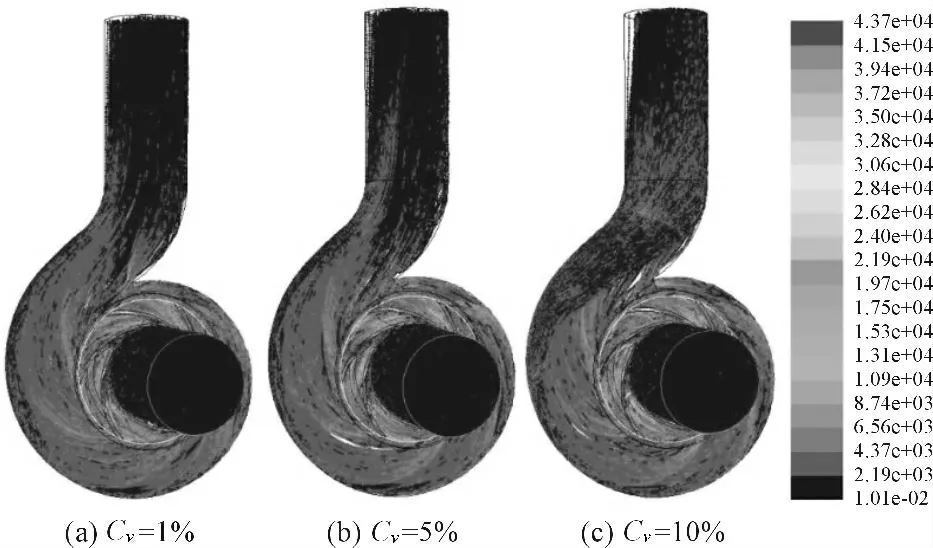
图8 颗粒雷诺数随浓度变化图(d=2.5 mm)

从图8 可以看出，随着浓度的变化，流道内颗粒雷诺数整体稍有减小。不同浓度下，颗粒雷诺数的变化趋势基本一致。从叶轮进口到出口，由于叶片的旋转运动使颗粒收到离心力的作用，固相颗粒和液相的分离比较严重，两相间的滑移速度会增大，导致颗粒雷诺数会增大。叶轮出口到蜗壳出口，固液两相间的滑移速度会逐渐减小，故颗粒雷诺数也逐渐减小。当Cv=1%时，颗粒雷诺数最小值为0.01，最大值为43 723.13。

3 结束语

本研究应用离散相模型，对固液两相流泵内颗粒运动规律进行了数值计算，得出不同固相参数工况下颗粒运动轨迹、固相速度分布规律以及颗粒雷诺数分布规律:

(1)颗粒运动轨迹随直径和浓度变化明显，随着直径和浓度的的增加，颗粒与蜗壳之间的碰撞次数减少。在叶轮流道内，颗粒易与叶片工作面发生碰撞。直径的变化对固相速度有一定影响，流道内的固相速度随着直径增大整体有减小的趋势，而浓度的增大对固相运动速度影响不明显。

(2)颗粒雷诺数随着直径增大而增大，随着直径增大，两相间滑移速度也会增大。颗粒雷诺数随着浓度变化会稍有降低，叶轮和蜗壳流道内两相分离严重，两相滑移速度比较大。

［1］赵斌娟，袁寿其，刘厚林，等.基于Mixture 多相流模型计算双流道泵全流道内固液两相湍流［J］.农业工程学报，2008，24(1):7-12.

［2］刘厚林，陆斌斌，谈明高，等.双流道泵内固液两相流动的数值模拟［J］.排灌机械，2009，27(5):297-301.

［3］ZHAO B J，HUANG Z F，CHEN H L，et al.Numerical investigation of solid-liquid Two phase flow in a non-clogging centrifugal pump at off-design conditions［J］.IOP Conference Series:Earth and Environmental Science，2012，15(6):062020.

［4］LI R N，WANG H Y，HAN W，et al.Study on solid-liquid two-phase unsteady flow characteristics with different flow rates in screw centrifugal pump［J］.IOP Conference Series:Materials Science and Engineering，2013，52(6):062002.

［5］ZHANG Yu-liang，LI Yi，ZHU Zu-chao，et al.Computational Analysis of Centrifugal Pump Delivering Solid-liquid Two-phase Flow during Startup Period［J］.Chinese Journal of Mechanical Engineering，2014，27(1):178-185

［6］WANG P W，ZHAO J，ZOU W J，et al.Experimental study and numerical simulation of the solid-phase particles' influence on outside characteristics of slurry pump［J］.IOP Conference Series:Earth and Environmental Science，2012，15(6):062057.

［7］刘建瑞，徐永刚，王董梅，等.离心泵叶轮固液两相流动及泵外特性数值分析［J］.农业机械学报，2010，41(30):86-90.

［8］PAGALTHIVARTHI K V，GUPTA P K，TYAGI V，et al.CFD prediction of erosion wear in centrifugal slurry pumps for dilute slurry flows［J］.The Journal of Computational Multiphase Flows，2011，3(4):225-246.

［9］汪家琼，蒋万明，孔繁余，等.固液两相流离心泵内部流场数值模拟与磨损特性［J］.农业机械学报，2013，44(11):53-60.

［10］李亚林，袁寿其，汤 跃，等.离心泵内示踪粒子运动的离散相模型模拟［J］.农业机械学报，2012，43(11):113-118.

［11］刘 娟，许洪元，唐 澍，等.离心泵内固体颗粒运动规律与磨损的数值模拟［J］.水力发电学报，2008，39(6):168-172.

［12］唐学林，余 欣，任松长，等.固-液两相流体动力学及其在水力机械中的应用［M］.郑州:黄河水利出版社，2006.

［13］李 昳，离心泵内部固液两相流动数值模拟与磨损特性研究［D］.杭州:浙江理工大学机械与自动控制学院，2014.

［14］唐 华.固液两相流离心泵内部流动特征的数值计算［D］.杭州:浙江理工大学机械与自动化控制学院，2014.