Logistic 模型预测稳定监测曲线型滑坡的应用

徐卫平 刘昆赟 吴永军

(国家林业局昆明勘察设计院，云南 昆明 650000)

0 引言

滑坡已成为我国较为普遍的地质灾害，国内诸多学者对滑坡的监测预警进行深入分析，提出了尖点突变模型［1］、Pearl 模型［2］、Verhulst 模型［3］等应用于滑坡的预测预报，都取得了良好的效果。考虑到滑坡降雨、库水位、地震等多种因素影响，滑坡的位移预测依然存在诸多难点，笔者在对稳定型监测位移曲线型滑坡研究的基础上，对该类型滑坡的曲线特征进行了深入分析，并将Logistic 模型应用于该类型滑坡的位移预测，具有一定的工程实际意义。

1 滑坡稳定型监测位移曲线特征

图1 稳定型监测位移曲线

如图1 所示，整个监测曲线在同一方向上(如:X 轴方向、Y 轴方向和Z 轴方向)的变形之和不为零，变形初始呈上升趋势，紧接着变形随时间增加而保持不变，宏观变形速度初始增加，而后变为零;加速度初始增加，而后变为零。按照力与变形之间的关系，分三种情况加以讨论:

1)当初始变形随时间增加时，总变形量很小或很大，推力也一直增加。这种曲线不存在。

2)当初始变形随时间增加时，总变形量很小，推力初始增加，紧接着推力恒定;这种监测曲线表明:该滑坡条块荷载—位移关系曲线处于比例极限应力空间之内，该条块处于稳定状态，且该滑坡条块为关键块体。当初始变形随时间增加时，总变形量较大，推力初始增加，紧接着推力恒定;这种监测曲线表明:该滑坡条块荷载—位移关系曲线处于残余应力状态，该条块处于不稳定状态。

3)当初始变形随时间增加时，总变形量很小，推力初始增加，紧接着推力下降，变形恒定;这种情况不成立。当初始变形随时间增加时，总变形量较大，推力初始增加，紧接着推力下降，变形恒定。这种监测曲线表明:该滑坡条块如果荷载—位移关系曲线呈理想弹～塑性状态，且该条块处于峰值极限应力空间上，该条块处于不稳定状态。

这种监测变形曲线的主要外因来自于降雨、地下水位变化、长江水位变化及施工开挖的影响。

2 Logistic 模型的建立

Logistic 模型又称Logistic 生长模型，是种群生态学的核心理论之一，由比利时数学家兼生物学家Verhulst PF 在修正Mathus模型的基础上提出的，也称为增长曲线模型［4］。该模型可以反映生物种群的增长过程，所以被广泛应用于生态学、生物繁殖、人口发展。同时，宰金珉等认为该模型反映了事物发生、发展、成熟然后到达一定极限的过程［5］，因此也被广泛应用于路基沉降、基坑沉降、地表沉降预测等岩土工程领域。

在时间预测序列中，Logistic 模型积分形式的数学表达式为:

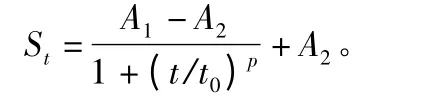
式中:St——t 时刻对应的位移预测值，其单位为长度单位;

t——时间;

A1，A2，p，t0——待定参数;

A2——最小值;

A1——最大值;

p——无量纲;

A1，A2——单位均为长度单位。

3 应用实例

大园子滑坡位于乌江岸坡一带，平面形态呈长条形，纵长1 100 m，横宽220 m，平均厚度8 m，面积24.2 ×104m2，体积193.6 ×104m3，为大型土质滑坡，主滑方向337°。坡体平均坡度角10°，主要组成物质为粉质粘土，透水性一般，潜在滑动面平均坡度角10°。

滑坡区属构造剥蚀低山河谷地貌形态，处于乌江左岸斜坡上，斜坡NNE 向延伸，往南逐渐增高，向北倾斜，逆向斜坡。最高点位于调查区南西角，高程725 m，最低点位于南侧的乌江主河道，高程175 m，相对高差550 m。该区为农耕区，人类工程活动强度小，故原始地形地貌保持较为完整。斜坡坡向337°，坡度上缓下陡，上部坡度角5°～10°，下部临江岸逐渐趋陡，坡度角10°～20°。

滑坡区斜坡坡体骨架由三叠系下统飞仙关组地层(T1f)岩层组成，其上覆松散堆积物主要为第四系残坡积层，滑坡区的后缘外围零星出露了飞仙关组，由灰黑色中厚层状灰岩夹黄褐色薄层状页岩组成，表层风化强烈，岩体较为破碎，强风化带厚1 m～3 m。滑坡区位于羊角背斜近轴部，岩层产状220°∠12°。

利用MATLAB 编写程序，对Logistic 曲线模型各参数进行最优估计，然后对指定时间点的位移量及最终位移进行预测，预测结果如图2 所示，从图2 中可以看出，Logistic 曲线模型的拟合精度较高，在中后期的拟合效果更好，对稳定型监测位移曲线型滑坡的中长期位移预测具有一定的效果。

滑坡位移预测与检验见表1。

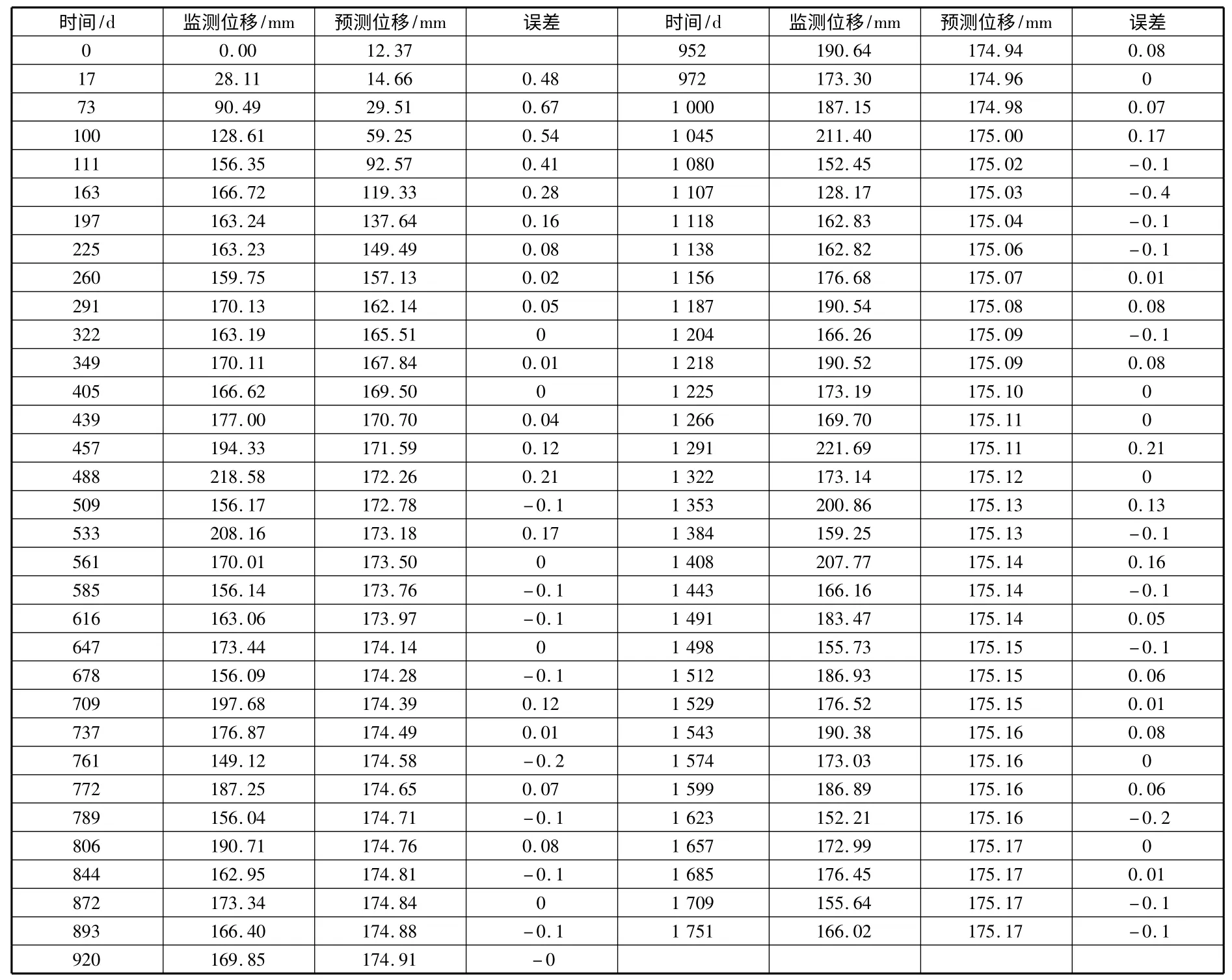
表1 滑坡位移预测与检验

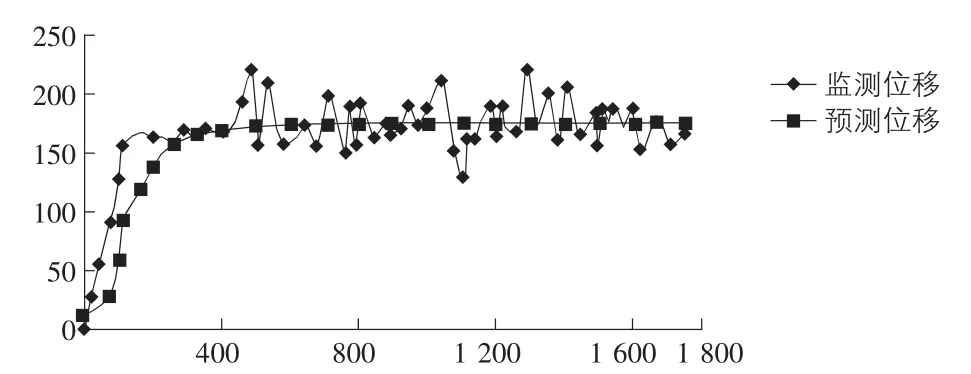
图2 滑坡预测位移量与时间的关系图

4 结语

基于稳定型监测位移曲线型滑坡位移的发展规律，将Logistic曲线模型运用于该类型滑坡的中长期预测，取得了较好的拟合效果，对同类型的滑坡位移预测具有一定的指导意义。

针对本文提出的预测模型，还有以下两点值得进一步研究:

1)Logistic 曲线模型的前期拟合效果较差，考虑对该模型进一步修正。

2)本文提出的方法在其他类型的滑坡位移预测的应用中还值得进一步研究。

［1］许建聪，尚岳全，郑束宁，等.强降雨作用下浅层滑坡尖点突变模型研究［J］.浙江大学学报，2005，11(39):1675-1679.

［2］孙景恒，李振明，苏万益.Pearl 模型在边坡失稳时间预报中的应用［J］.中国地质灾害与防治学报，1993，2(4):36-41.

［3］温 文，吴旭彬.Verhulst 模型在黄茨滑坡临滑预测中的应用［J］.人民珠江，2005(5):38-40.

［4］阎慧臻.Logistic 模型在人口预测中的应用［J］.大连理工大学学报，2008，27(4):333-335.

［5］朱志铎，周礼红.软土路基全过程沉降预测的Logistic 模型应用研究［J］.岩土工程学报，2009，6(31):965-969.