基于接收信号强度（RSSI）的室内二次定位方法*

陈淑敏，乔晓田，毛 佳，徐元欣*

（1.浙江理工大学信息电子学院，杭州 310018；2.浙江大学信息与通信工程研究所，杭州 310027）

基于接收信号强度（RSSI）的室内二次定位方法*

陈淑敏1，乔晓田2，毛 佳2，徐元欣2*

（1.浙江理工大学信息电子学院，杭州 310018；2.浙江大学信息与通信工程研究所，杭州 310027）

提出一种用于室内定位的基于接收信号强度（RSSI）的二次定位方法。首先利用全网中已有节点的信息，建立已知节点的初始路径传播损耗指数，采用统计中值滤波来减少RSSI的粗大误差和干扰，然后利用RSSI初次定位的位置结果对传播损耗指数进行再次修正，最后进行二次定位解算，显著提高了未知节点的定位精度。通过仿真和搭建实验平台验证了该算法的有效性。

无线传感器网络；接收信号强度指示；路径传播模型；二次定位

近年来，随着科学技术的高速发展和人们生活水平品质的不断提高，定位服务市场发展迅速，定位服务的需求量也呈现飞速发展的趋势，基于位置的服务LBS（Location-Based Services）受到了人们的广泛关注［1］。对于室外环境下的定位，全球导航卫星系统GNSS（Global Navigation Satellite System）［2］能够提供精确定位，应用非常广泛。然而对于建筑密集区或者室内环境，卫星信号强度由于受到建筑物的影响而大大衰减，无法较好的使用甚至不能完成定位。目前WiFi被广泛用于城市公共接入热点，以及家庭网络和办公网络，将它运用于定位技术中，将大大降低系统的部署成本，并能保证定位精度和覆盖率。

室内的节点定位技术，根据定位机制的不同，分为基于测距（range-based）和非测距（range-free）的方法［2］。基于非测距的方法利用网络连通性等信息实现定位，在成本和功耗等方面有一定的优势，但定位精度相对较低，如APIT（Approximate Point-In-TriangulationTest）［3］、DV-Hop（DistanceVectorhop）［4］等；基于测距的方法通过测量节点间的距离或角度等信息来计算节点的位置，定位精度相对较高［5］，如 TOA（Time of Arrival）、TDOA（Time Difference of Arrival）、AOA（Angle of Arrival）、RSSI （Received Signal Strength Indicator）等。

基于接收信号强度（RSSI）的定位技术属于基于测距的方法，通过未知待定位节点接收的来自已知节点的无线信号强度值，采用路径传播模型，将接收信号强度值转换为距离，最后利用三边测量法等方法估计未知节点位置坐标。该方法不需要对收发双方增加额外的硬件，特别是Wifi系统，只利用待定位节点本身的数据通信过程就可完成定位，易于实现。早期Hightower等人［6］通过RSSI方法来估计两点间的距离，通过节点间的相互位置来进行定位，由于室内环境的复杂性，该方法的精度严重受到大干扰、多径反射、非视线问题等因素的影响。文献［7］采用线性回归分析RSSI传播模型中的两个参数（距离发射节点1 m的RSSI值和路径损耗指数），信号仍受到环境因素很大的影响。文献［8］针对测距结果引入抗差估计理论，对不同的误差进行剔除和降权等处理，提高了定位精度。针对上述相关研究的情况，本文首先采用中值滤波来减少测量误差，然后在常规初次定位基础上提出一种利用一次定位的结果进行二次定位的方法，充分利用全网中已有的信息，来尽量消除定位过程中对环境参数的依赖性，通过采用两次定位来减小与未知节点真实位置的误差，从而提高定位的精度。

1 初次定位

1.1 室内传播模型

通过理论分析并对大量的实验数据进行计算机拟合，发现无论是在室内还是室外接收端接收到信号的强度值与收发双方的距离是成一定对数变化的关系［9］，可建立接收端与发射端之间的传播路径损耗模型为：

式中：γ为路径传播损耗指数，它表示了路径损耗与距离增长的指数比。γ值直接依赖于具体的传播环境；d0为参考距离，对于室内一般设为1 m。PL（d0）是参考距离d0处的路径传播损耗，可实际测量出；d是接收端与发射端之间的实际距离。Xδ是背景噪声，是一个服从N（μ，σ2）的高斯随机变量。

由于实际中的三维空间方程组和未知数个数较多，但定位原理与二维类似，为描述方便下文均以二维空间为例介绍。节点位置的简易网络模型如图1所示，BS1到BS5为已知节点，MS为未知节点，实线代表两两已知节点之间的通信，虚线表示未知节点与已知节点间的通信。在整个网络中，每个已知节点周期性地发射信号，包括节点名称和绝对位置。当网络中的其他节点收到对应的信号后，就可以根据已知节点位置坐标和接收到的信号强度来计算两点间的路径损耗指数，利用信号传输模型获得节点间距，最终通过定位算法得到未知节点的位置。

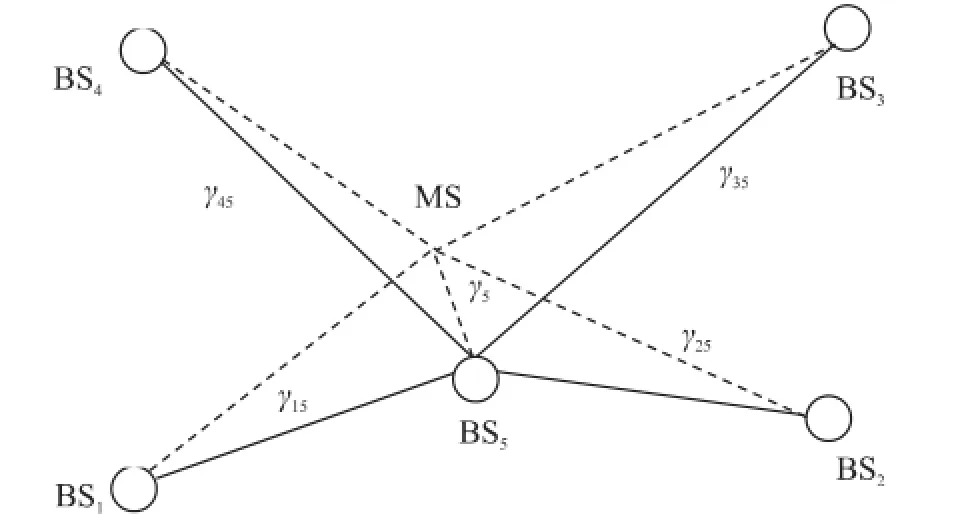
图1 节点位置示意图

1.2 节点间的路径损耗指数

根据对数距离路径损耗模型，可以计算出已知节点间路径的路径传播损耗值γi，j，当未知节点加入时，不同已知节点到未知节点的初始平均路径损耗指数可以按式（2）进行近似得到，其中M为定位区域内已知节点数目。

1.3 采用统计中值减少RSSI的误差

由于室内发射引起的多径传播、非视距传播、其他电子设备信号以及人体干扰使得接收端的RSSI强度值存在一定的随机性和不稳定性［10］。因此，在进行定位前，必须对接收到的信号强度值进行处理，减少随机性和不稳定性给定位结果带来的误差。

未知节点记录多次接收到某已知节点信号强度的测量值，采用基于统计中值的误差分析方法［11］有助于显著减少粗大误差和随机误差的影响。具体步骤如下：

①首先对N个测量值RSSIi（i=1，2，…，N）进行大小排序，得到序列的中值RSSImid。

②计算第i个测量值所占的权重wi，如下式所示。由于有些包含误差的信号测量值仍有可能与中值接近，因此将各个信号值与中值的偏差平方均值作为阈值T，当偏差平方大于阈值时，权值由偏差平方决定，反之则由阈值决定。显然，测量值与中值相差越大，权值越小；测量值越接近中值，权值越大。

③将每个测量值与加权系数相乘，得到最终的加权平均值作为未知节点接收到该已知节点的信号强度：

采用MATLAB将本文的统计中值滤波方法与常用的均值滤波方法和t检验滤波方法［12］进行在不同粗大误差比例下的对比仿真：假定有50个信号强度测量数据序列，随机从2%到20%的数据（即1 到10个）加入粗大误差，其余数据在真实值（设为39 dB）的基础上加入均值为0，标准差为8 dB的高斯噪声。结果如图2所示，图2（a）表示加入正向粗大误差，误差数值设为信号真实值的两倍，图2（b）表示加入双向粗大误差，误差数值随机设为信号真实值的两倍或1/2，横坐标代表粗大误差在整个测量序列中所占比例，纵坐标代表滤波后的相对误差。可以看出，当粗大误差所占比例较小时，本文方法与t检验法的性能相近，但当粗大误差所占比例大于等于10%时，本文采用的统计中值滤波方法性能具有明显优势。

在此基础上，进一步仿真高斯噪声与误差的关系：假定正向粗大误差所占比例为10%，高斯噪声标准差从4 dB到12 dB，其余数据保持不变，结果如图3所示。横坐标代表高斯噪声标准差，纵坐标代表滤波后的相对误差。综合实验结果可以看出，基于统计中值的误差分析方法相比其余误差处理方式更优，结果更接近真实值，因此本文选择基于统计中值的误差分析法作为信号强度测量阶段的误差处理方式。

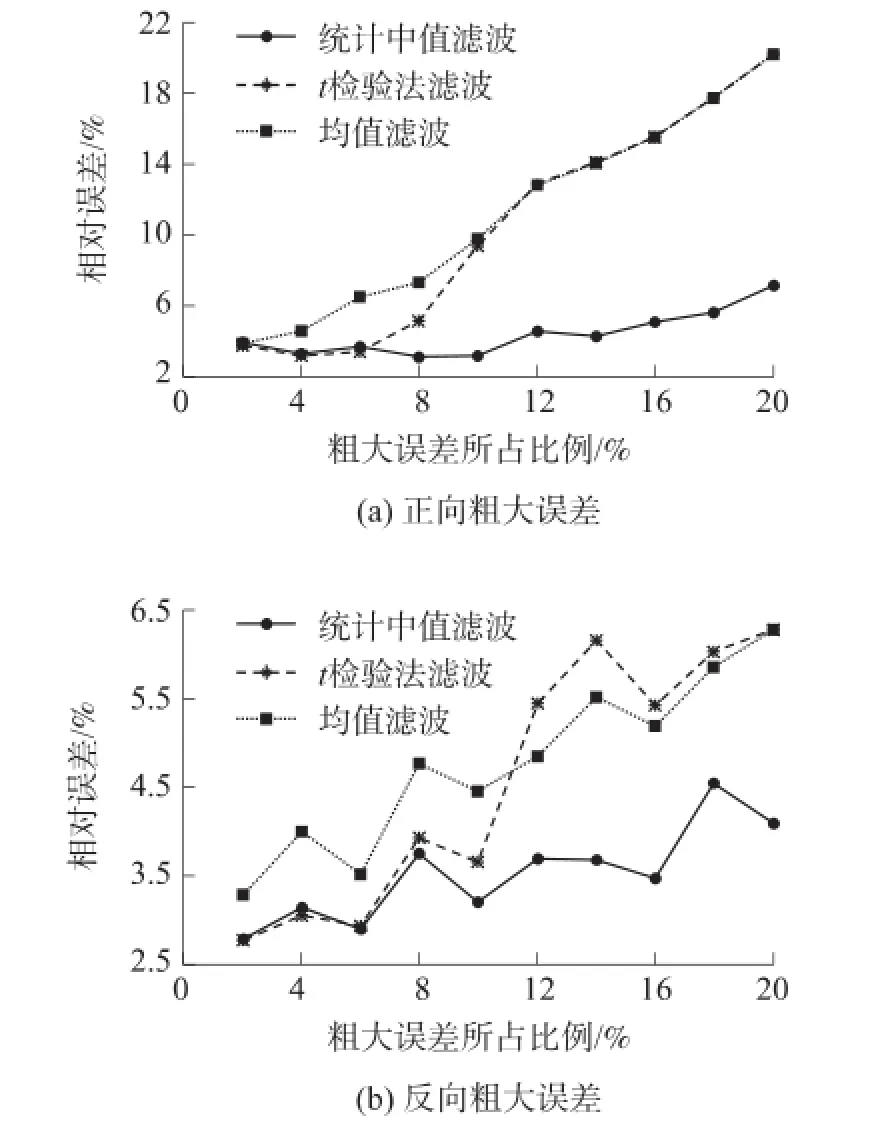
图2 不同误差处理方式与粗大误差数量的关系

图3 不同误差处理方式与高斯噪声标准差的关系

1.4 计算未知节点初次位置

按上面1.3节滤波方法得到未知节点从各已知节点接收的信号强度，以及按式（2）求得的平均路径损耗指数作为初始值，然后可根据式（1）的衰减理论模型计算得到未知节点到各已知节点的初次距离估计值di（i=1，2，…，M），然后通过位置解算方法就可获得未知节点的坐标值，比如三边定位法和最小二乘法等。

常规的线性最小二乘法任意选择一个已知AP节点作为参考节点，其他AP节点的定位圆方程减去参考节点定位圆方程，得到N-1个线性方程。由于我们得到的距离值有较大误差，所以选取常规最小二乘法会带入更大的定位误差。本文首先取所有距离测量值的平均值，然后从所有方程中减去这个平均值，得到N个线性方程，再进行最小二乘法的求解。这样以避免选择远距离和高测量误差的已知节点作为参考点，对于定位误差的抑制有一定的效果。

假设已知节点的坐标设为（xi，yi），i=1，2，…，M，未知节点坐标设为（x，y），则可以建立如下方程组：

当M≥3时可得如下线性方程：

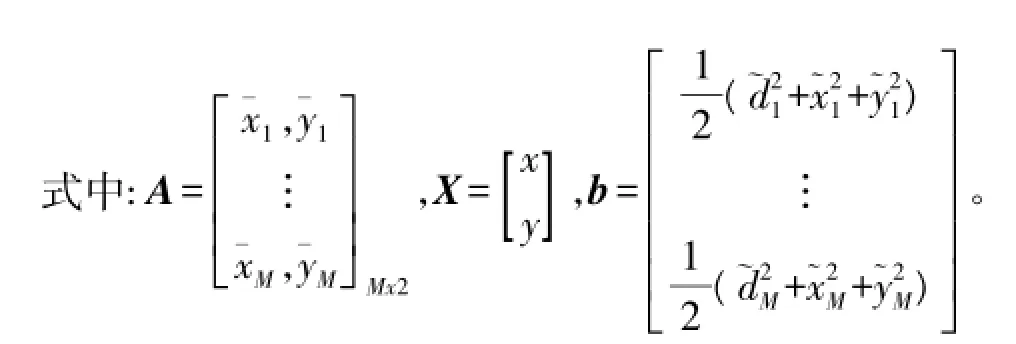
2 二次定位

由于未知节点到已知节点的路径损耗指数估计不准确，初次定位的结果存在较大的误差。因此需要在初次定位的基础上，进行二次定位。未知节点根据初始定位值在网络中寻找与自己距离最近的已知节点。若发现未知节点距离某个已知节点很近，而距离其他已知节点很远，则将此已知节点的路径损耗指数作为未知节点到其他节点的路径损耗指数，否则取加权平均值［13］。

以图4为例，根据前面得到的未知节点初始估计位置，对已知节点1的路径损耗指数进行二次修正。当Φ1较小时，BS1到未知节点的传播路径与BS1到BS2的传播路径相似，因此直接将γ1更新为γ12。当Φ1较大时，选择与未知节点次近的BS3作为参考，进行加权更新，如下式所示。阈值θ根据不同环境进行不同的设定，一般在10°～20°之间。

得到新的路径损耗指数之后，再按1.4节的方法重新计算未知节点与已知节点之间的距离值，完成未知节点和已知节点间距的估计，最后按式（10）得到更新后的未知节点的位置值。

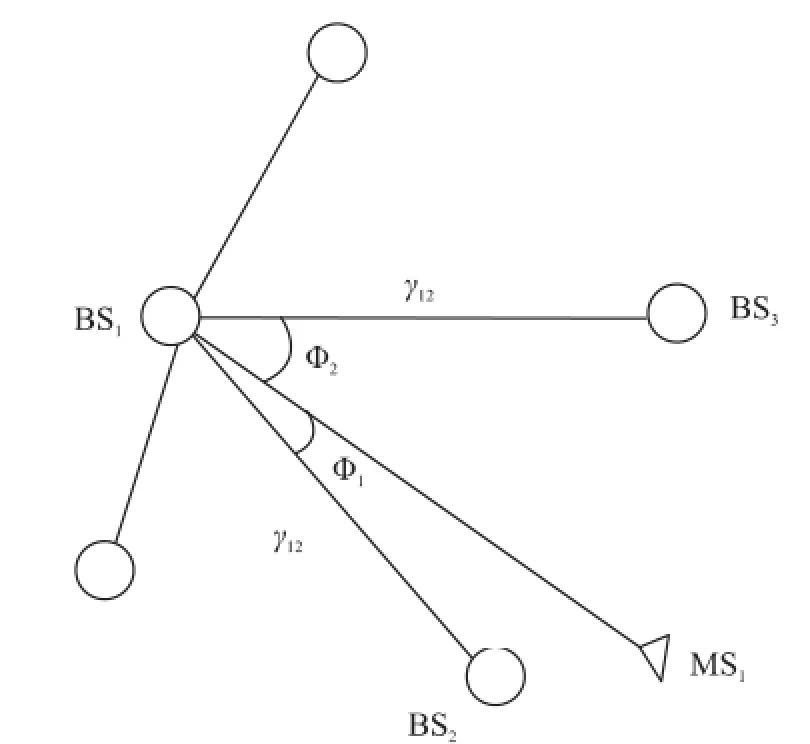
图4 未知节点的路径损耗指数二次修正

3 仿真及实验

本文采用MATLAB对定位算法进行了相应的仿真，并同相关方法进行了比较，验证本文提出的算法性能。将仿真环境设为12 m×9 m的矩形区域，有序摆放若干个已知节点，随机摆放1个未知节点，如图5所示。为了更好地模拟真实环境，将整个环境分为9个区域，不同区域的路径传播损耗指数不同（通常在2.5～3.5之间）［14］。当未知节点加入时，根据模拟的路径传播损耗指数生成接收信号强度。根据多次采集的RSSI值进行统计分析，噪声的典型标准差为6 dB，因此仿真中加入均值为0，标准差为6 dB的高斯噪声。共进行50次仿真，每次仿真时未知节点的位置都随机选取，并且对信号强度值进行20次测量，采用前面的统计中值方法减少粗大误差和随机误差的影响，进行初次定位和二次定位。

图5 各节点的摆放情况

对5个已知位置节点的初次定位和二次定位的误差更详细的对比如图6和表1所示。可以看出，二次定位的结果明显优于初次定位（即常规的一次定位）。

图6 初次定位与二次定位结果比较

表1 仿真定位结果误差分析（单位：m）

将三角形质心定位算法［15］（记为RSSI-TC）与本文的改进算法（记为RSSI-Ⅱ）进行对比，性能比较如表2所示，其中也列入了初次定位的结果（记为RSSI-Ⅰ）。从表2可以看出，本文提出的定位算法在定位精度方面更有优势。

表2 算法性能比较 单位：m

我们在嵌入式Linux的移动设备上实现了本文所提出的定位算法，组建了一个定位示范平台。采用友善之臂的Mini2440开发板和北京华大的WiFi接口控制器芯片HED08W04SU开发已知和未知节点设备终端，在实验室6.3 m×8.8 m的范围内布置5个已知位置节点，如图7所示。中间两排的书桌上存在高0.6 m的挡板，将实验室划分为不同的区域。以图7左下角为原点建立直角坐标系，书架所在墙面为x轴，第一排书桌所在墙面为y轴。5个已知位置节点的坐标分别为AP1（1.5，1.5），AP2（0.9，5.5），AP3（5.3，3.8），AP4（6.9，0.6），AP5（7.5，5.2）。

分别在A（1.7，2.0），B（1.0，6.1），C（5.0，3.5），D（6.0，1.0），E（7.0，5.0）5处位置进行定位实验，每个位置定位10次，结果如表3所示。

表3 定位结果误差分析表（单位：m）

图7 实验室场景图

根据表3，综合5个位置的定位结果，平均误差为0.951 m。测试点A，B周围没有人员走动，电子设备干扰低，平均误差较小，误差标准差小说明定位的稳定性高。而测试点C处在实验室中部，周围人员走动多，处于多台电脑中，干扰大，误差的标准差较大，定位结果较不稳定。

在实际测量过程中，各个AP节点的硬件差异性以及AP天线的方向性是最大的误差来源，同时AP端测量接收信号强度的误差也对定位的结果造成了影响。通过定位实验的结果可看出，本文提出的基于接收信号强度中值滤波、改进最小二乘以及二次定位的方法具有可行性。

4 结论

本文通过对比几种常见的信号传播模型，选择了对数距离路径损耗模型，利用全网已知节点的相互接收信息，得到室内信号初步传播特性。采用统计中值对节点的接收信号强度进行加权滤波，降低粗大误差和随机干扰的影响。建立测距的线性方程组按改进最小二乘进行位置解算，得到未知节点的初次定位。根据初次定位，进一步修正路径传播损耗指数，然后进行二次定位解算得到未知节点的位置结果，显著减小了未知节点的定位误差。最后通过MATLAB仿真并在实验室搭建了实验场景，验证了算法的实际有效性，对室内定位的研究具有参考价值。

基于RSSI的室内定位方法可以利用现有的基础设施，不需要对收发双方增加额外的硬件，可以快速推向应用，但实际应用中定位的精度和稳健性仍还需进行更深入研究和实用化完善的工作。

［1］ 宁焕生，王炳辉.RFID重大工程与国家物联网［M］.机械工业出版社，2009.

［2］ Han G，Xu H，Duong T Q，et al.Localization Algorithms of Wireless Sensor Networks：a Survey［J］.Telecommunication Systems，2013，52（4）：2419-2436.

［3］ 冯秀芳，崔秀锋，祈会波.无线传感器网络中基于移动锚节点的APIT的改进定位算法［J］.传感技术学报，2011，24（2）：269-274.

［4］ 温江涛，范学敏，吴希军.基于RSSI跳数修正的DV-Hop改进算法［J］.传感技术学报，2014，27（1）：113-117.

［5］ Garg V，Jhamb M.A Review of Wireless Sensor Network on Localization Techniques［J］.International Journal of Engineering Trends and Technology，2013，4（4）：1049-1053.

［6］ Hightower J，Want R，Borriello G.SpotON：An Indoor 3D Location Sensing Technology Based on RF Signal Strength［D］.UW CSE 00-02-02，University of Washington，Department of Computer Scienceand Engineering，Seattle，WA，2000，1.

［7］ Minghui Z，Huiqing Z.Research on Model of Indoor Distance Measurement Based on Receiving Signal Strength［C］//Computer Design and Applications（ICCDA），2010 International Conference on. IEEE，2010，5：54-58.

［8］ 张亚明，史浩山，刘燕，等.基于抗差估计方法的WSN节点定位算法研究［J］.传感技术学报，2014，27（8）：1088-1093.

［9］ Noh A S I，Lee W J，Ye J Y.Comparison of the Mechanisms of the ZigBee's Indoor Localization Algorithm［C］//Software Engineering，Artificial Intelligence，Networking，and Parallel/Distributed Computing，2008.SNPD'08.Ninth ACIS International Conference on. IEEE，2008：13-18.

［10］刘召伟，徐凤燕，王宗欣.基于参数拟合的室内多用户定位算法［J］.电波科学学报，2008，23（6）：1090-1094.

［11］严筱永，钱焕延，张燕，等.一种减少测距误差的传感器网络定位算法［J］.计算机测量与控制，2011，19（8）：2058-2060.

［12］王文周.未知σ，t检验法剔除异常值最好［J］.四川工业学院学报，2000，19（3）：84-86.

［13］Tran-Xuan C，Vu V H，Koo I.Calibration Mechanism for RSS Based Localization Method in Wireless Sensor Networks［C］//Advanced Communication Technology，2009.ICACT 2009.11th International Conference on.IEEE，2009，1：560-563.

［14］Mao G，Anderson B D O，Fidan B.Wsn06-4：Online Calibration of Path Loss Exponent in Wireless Sensor Networks［C］//Global Telecommunications Conference，2006.GLOBECOM'06.IEEE. IEEE，2006：1-6.

［15］林玮，陈传峰.基于RSSI的无线传感器网络三角形质心定位算法［J］.现代电子技术，2009，32（2）：180-182.

陈淑敏（1976-），女，硕士，浙江理工大学信息电子学院讲师。主要研究方向为无线通信、定位同步、视觉与网络信息处理；

徐元欣（1974-），男，博士，浙江大学信息与电子工程学系副教授。主要研究方向为通信网络系统、跨层技术、水声通信，xuyx@zju.edu.cn。

RSSI-Based Twice Location Method for Indoor Positioning*

CHEN Shumin1，QIAO Xiaotian2，MAO Jia2，XU Yuanxin2*
（1.Faculty of Informatics and Electronics，Zhejiang Sci-Tech University，Hangzhou 310018，China；2.Institute of Information and Communication Engineering，Zhejiang University，Hangzhou 310027，China）

A twice location method based on RSSI is presented for indoor positioning.The proposed method estimates the path propagation parameters upon the existing nodes'information，and a statistics median filter method is used to remove outliers and reduce random error.Then the path propagation parameters are updated by the result of the first RSSI location.Finally，position of the unknown node is determined by second location.The twice location algorithm based on RSSI plays a role under many conditions，and obtains certain positioning precision.We have validated the positioning effectiveness of the method by simulation and experimenting on the embedded platform.

wireless sensor networks；received signal strength indication；path propagation model；twice location EEACC：5210C；6330

TN92

A

1004-1699（2015）04-0572-06

10.3969/j.issn.1004-1699.2015.04.020

项目来源：浙江省教育厅科研项目（Y201226131）；浙江省科技计划项目（2014C31060）

2014-11-02 修改日期：2015-01-05