均值计数模型下汽车保险索赔频数的估计方法

赵晓兵, 刘 伟

(浙江财经大学数学与统计学院,浙江 杭州 310018)



均值计数模型下汽车保险索赔频数的估计方法

赵晓兵, 刘 伟

(浙江财经大学数学与统计学院,浙江 杭州 310018)

汽车保险的索赔频数预测问题是非寿险精算理论和应用研究的一个重要内容。但是,在含有高维附加信息的情形下,传统的估计方法就不再适用。本文在均值计数模型基础上,利用凸惩罚函数进行变量选择,找到影响车险索赔频数的显著性因子,并通过模拟和实例分析来评价该模型和所提出的方法的可行性。

汽车保险;均值计数模型;凸惩罚;变量选择;估计方程

一、引 言

汽车商业保险是对机动车辆由于自然灾害或意外事故所造成的人身伤亡或财产损失承担赔偿责任的一种保险业务。随着汽车数量的猛增,车险市场呈现出快速发展的态势。汽车保险更是财产保险的第一大险种,部分公司的汽车保险保费收入占其财产保险总保费收入的60%以上。关于汽车保险定价方法的研究一直以来都是非寿险精算理论及应用研究的重点内容。

在目前的汽车保险定价实务中,对车险索赔频率和索赔强度的预测是两个主要研究问题,流行的研究方法是利用广义线性模型方法[1][2]。虽然广义线性模型有现成的统计软件可用,也可以对参数估计的结果进行直观的解释,但是,该方法需要假定已知因变量和解释变量之间的某种联系函数,而目前采用的函数形式却比较有限。随着现代统计方法的大量出现,以及数据收集方式的更新,使得新类型的数据往往包含大范围的附加信息,即所谓的“高维协变量”[3]。在这种背景下,传统的广义线性模型往往不再适用。而且由于广义线性模型不能自动识别解释变量之间的交互作用,导致建模过程比较耗时。除广义线性模型之外,神经网络模型也是研究汽车保险索赔问题的常用研究方法之一。但神经网络模型的计算较为复杂,同时也很难对协变量的回归系数给出直观的解释(Faraway,2006;Werner and Modlin,2010;孟生旺,2007)[4][5][6]。

针对现有汽车保险索赔频数估计方法中存在的局限,本文基于澳大利亚MAA公司(The Motor Accidents Authority)的一组综合险(comprehensive insurance)索赔数据,将Wang、Qin and Chiang(2001)[7]以及Huang and Wang(2004)[8]的模型推广到允许含有高维协变量存在的情形,在此基础上提出一个新的评估方法。该模型有两个显著特点:一是允许高维协变量的存在,可以通过变量选择得到模型的稀疏表达,找到影响索赔频数的显著性因子,提高模型整体的预测精度。二是对未知的基准函数不进行任何参数假定,并且在降维的过程中不需要知道基准函数的具体形式,以便对车险索赔频数做出更稳健的估计。

二、模 型

在索赔频数或者复发事件研究中,我们常常采用Cox型强度函数的计数过程。假定因变量Ni(i=1,2,…,n)为汽车保险索赔频数,解释变量Xi1,Xi2,…,Xip为影响车险索赔频数的风险因子。为了分析该索赔数据,Huang and Wang(2004)[8]提出了如下模型:

(1)

其中,Xi=(Xi1,Xi2,…,Xip)T,βi=(β1,β2,…,βp)T,t=Yi∧τ为观测时间,Yi为删失时间,τ为观测的终止时间,λ0(t)是未知的基准函数(baseline),λ(t|Xi)是强度率函数。上述模型常常被称为Cox型比例危险模型。

然而此模型也存在一些局限,例如,我们常常需要假定其协变量是低维的。当含有高维协变量时,该模型往往不再适用。基于此,本文对该模型进行一般化推广,即允许有高维协变量的存在。Zhao and Zhou(2014)[9]对含有高维协变量的Cox模型下的系数估计方法进行了深入研究,提出如下的多指标模型:

(2)

其中,Ψ为完全未知的联系函数。首先利用非参数方法对未知的基准函数Λ0(t)做出估计,其次使用充分降维(sufficient dimension reduction-SDR)获得协变量的中心降维子空间的结构维数和基方向,最后通过局部回归估计完全未知的联系函数Ψ。

注意到Zhao and Zhou(2014)[9]对Λ0(t)的估计需要使用每次索赔发生的具体时间数据,而在目前的精算实务中,保险精算数据往往只含有累积的索赔次数,而并不特别关心每次索赔具体发生的时间点。因此,在本文中,我们只需要对协变量进行降维,而不再关注基准函数Λ0(t)的估计。假设一个均值计数模型,即假设到时刻t为止的累积索赔次数Ni(t)有如下的均值计数结构:

(3)

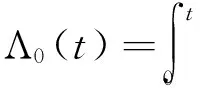
另外,SDR可以有效克服高维协变量情形下“维数祸根”的影响,且不需要对模型有任何参数假定,在降维的过程中也充分考虑了响应变量的因素,保留了更多的回归信息。但类似于主成分分析,SDR是通过寻找自变量的若干线性组合来达到降维目的的,因此我们不易得到降维系数的直观解释。为了找到影响汽车保险索赔频数的显著性因子,赋予模型以直观的解释,同时提高模型整体的预测精度,本文考虑另一种方法,即通过优化一个带“惩罚”函数的“损失”来达到变量选择的目的,该方法也是目前文献中另外一个受到广泛重视的解决高维协变量问题的有效方法。受Fan and Li(2001)[10]惩罚对数似然函数思想的启发,本文在模型(3)的基础上,对Sun and Wei(2000)[11]提出的估计方程做出惩罚,以得到β的稀疏估计。本文的显著优点在于:一是可以允许有高维协变量的存在,二是通过惩罚函数挑选显著性变量时不需要依赖基准函数baseline。

注意到模型(1)和(3)虽有上述数学表达式上的联系,但实际上它们却有很大的差别。模型(1)是一个基于非平稳泊松分布的计数过程,模型(3)则为不需要关于分布作任何假设的均值计数模型。另外,在估计方法上,模型(1)和(2)均需要知道每次索赔发生的具体时间点,而模型(3)却允许索赔发生的时间点完全未知。因此无论是在统计建模还是估计方法上,模型(3)比模型(1)都更具灵活性和更一般化。

三、模型估计

本节将利用凸惩罚函数方法来进行变量选择,得到影响车险索赔频数的显著性因子及相应的系数估计。在模型(3)基础上,为了得到参数向量β的估计,Sun and Wei(2000)[11]提出了如下的无偏估计方程,该方法的最大特点是不涉及未知的基准函数Λ0(t),从而不需要每次索赔的具体发生时间点。中心化协变量Xi后,该估计方程定义如下:

为了得到β的估计,Tong and He等(2009)[12]提出如下的迭代公式:

β(l+1)=β(l)+{nA(β(l))+n∑(βl)}-1Q(β)

(4)

其中,βj为第l次迭代β(l)的第j个分量。为了得到调整参数,我们在以上每一次迭代中都使用广义交叉验证方法,其定义为:

e(λ1,…,λd)=tr[{A(β)+∑(β)}-1A(β)]

其中,tr为求矩阵的迹,即矩阵主对角线元素之和。则调整参数(λ1,…,λd)可以定义为如下统计量的最小值:

将初值β(0)带入GCV,在得到λ1,λ2,…,λd后,即可计算A(β)与∑(β),再带入(4)式,迭代至收敛,即可得到β的惩罚估计。

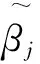
四、数值模拟

(一)维数为6的数值模拟

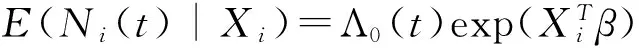
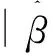
表1 β的估计值

(二)维数为10的数值模拟

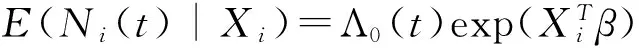
表2 β的估计值

五、实例分析

本节基于澳大利亚MAA公司(TheMotor Accidents Authority)的一组综合险的索赔数据,研究车险索赔频数对影响因素的响应关系。该组数据共含有1446位投保人在1993年度的索赔信息,Jong and Heller(2008)[14]利用Copula模型分析过该组数据。本文将利用模型(3)再次来分析该组数据,我们将通过惩罚函数来挑选显著性因数变量,从而达到降维目的。

以一份汽车保险合同在一个固定保险期内(一个保险期)的最终索赔频数为因变量,影响因素为所有可能的变量,共17个变量。几个比较重要的变量如下:

(1)被保险人在该保险合同以前(不包括该保险合同期内的)的索赔金额;

(2)被保险人性别(0表示男性,1表示女性);

(3)保单维持期(以一年为一个保单合同期,表示被保险人在保险公司的合同连续维持了几年);

(4)婚否(即被保险人在观测期内是否结婚,0表示未婚,1表示已婚);

(5)父母健在(0表示父母去世,1表示父母健在);

(6)居住时间(以年为单位,表示被保险人在同一处所居住的最长时间);

(7)延误(即处理完索赔的耽误时间);

(8)观测期数(即连续观测了多少时间,以年为单位,一年为一期)。

表4 系数估计的值

由表4可以看出,对索赔频数影响较大的变量主要有:前期的索赔金额、被保险人性别、被保险人婚否、被保险人父母是否健在以及最高受教育程度。通过以上估计,我们可以得到如下结论:

(1)前期的索赔金额。在变量选择得到的系数估计中,前期索赔金额的系数为0.1658,由此我们可知,该变量对索赔频数有显著性影响。这主要是由于,在正常情况下,被保险人在过去的行为会自觉延续到现在,这与行为经济学的基本假设相吻合。

(2)被保险人性别。在变量选择得到的系数估计中,性别的系数为0.5047,这说明性别对交通事故的发生有较为显著的影响,这主要是由于男女性格差异、行为模式等的不同造成男女在交通事故的发生次数及严重程度上有明显的区别。

(3)被保险人是否结婚。在表4中,婚否对索赔频数的影响系数为0.4783,这说明是否结婚对因变量有较为显著的影响,这主要是由于结婚使被保险者的家庭责任感上升,从而自觉遵守交通规则,减少交通事故的发生以及汽车保险的索赔次数。

(4)父母健在。从惩罚估计的结果来看,该变量的系数估计为0.2167,这与我们直观上的感觉并不一致,同被保险人是否已婚相同,这主要是因为父母的健在使被保险人有更多的归属感及家庭责任感,从而影响到交通事故的发生及汽车保险的索赔。

(6)最高受教育程度。从表4可以看出,最高受教育程度对索赔次数有非常显著的影响。这是因为随着受教育程度的提高,更高素质的被保险人会更加自觉地遵守交通法规,从而对索赔次数的减少产生积极的影响。

(5)保单维持期。理论上,保单维持期越长,索赔次数越大,保险理赔越高。然而,被保险人性别、婚否、受教育程度等也对索赔次数有很大的影响,从而使得保单维持期对索赔次数的影响不是那么显著。另外一个解释是,由于汽车保险奖惩系统(Bonus-Malus System-BMS)的存在,留在同一保险公司的长期客户都是“表现良好”的客户。

六、总 结

本文中,我们提议了一个汽车保险索赔频数的均值计数模型,该模型允许每次索赔具体发生时间点缺失,同时也允许有高维协变量的存在。该方法无论从模型建立还是统计方法上讲都更具一般性和灵活性。我们利用凸惩罚变量选择方法对高维协变量进行降维,得到回归系数的稀疏估计,该方法提供了一种处理高维情形下车险索赔数据的另外一种选择。在本文中,我们主要研究了汽车保险的索赔次数,而没有考虑每次索赔的具体金额,这将是我们以后要继续研究的问题。

[1] Lin D Y. Linear regression analysis of censored medical costs[J]. Biostatistics,2000,1(1):35-47.

[2] Lin D Y. Regression analysis of incomplete medical cost data[J].Statistics in Medicine,2003,22(7):1181-1200.

[3] 赵晓兵,王伟伟.高维附加信息下的商业医疗保险费用评估模型和方法[J].财经论丛,2013,(4):58-65.

[4] Faraway J. Extending the Linear Model with R[M]. Chapman & Hall/CRC,2006.

[5] Werner G., Modlin C. Basic Ratemaking[M]. Casualty Actuarial Society,2010.

[6] 孟生旺.广义线性模型在汽车保险定价中的应用[J].数理统计与管理,2007,(1):24-29.

[7] Wang MC, Qin J and Chiang CT. Analyzing recurrent event data with informative censoring[J]. Journal of the American Statistical Association,2001,(96):455-464.

[8] Huang CY, Wang MC. Joint modeling and estimation of recurrent event processes and failure time data[J]. Journal of the American Statistical Association,2004,(99):1153-1165.

[9] Zhao XB, Zhou X. Sufficient dimension reduction on the mean and rate functions of recurrent events[J]. Statistics in Medicine,2014,33(21),3693-3709.

[10] Fan JQ, Li RZ. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of the American Statistical Association,2001,(96):1348-1360.

[11] Sun JG, Wei L. Regression analysis of panel count data with covariate-dependent observation and censoring times[J]. Journal of the Royal Statistical Society: Series B,2000,(62):293-302.

[12] Tong XW, He X, Sun LQ, Sun JG. Variable selection for panel count data via non-concave penalized estimating function[J]. Scandinavian Journal of Statistics,2009,(36):620-635.

[13] Li RZ, Liang, H. Variable selection in semiparametric regression modeling[J]. The Annals of Statistics,2008,(36):261-286.

[14] Jong, P. and Heller, G. Z. Generalized Linear Models for Insurance Data (International Series on Actuarial Science)[M]. Cambridge,2008.

(责任编辑:原 蕴)

Estimation of Car Insurance Claim Frequency under the Mean Count Model

ZHAO Xiao-bing, LIU Wei

(School of Mathematics & Statistics, Zhejiang University of Finance & Economics, Hangzhou 310018, China)

Prediction of car insurance claim frequency is a focus of theoretical and empirical research of non-life actuarial studies. However, owing to the high-dimensional information involved, traditional models and estimation methods no longer apply. In this paper, some significant factors of car insurance claim frequency are identified through the variable selection method with convex penalty function based on the mean count model. A small simulation and a real data analysis are conducted to assess the feasibility of the proposed model and methods.

car insurance; mean count model; convex penalty; variable selection; estimate function

2014-08-27

国家自然科学基金资助项目(11271317);浙江省自然科学基金资助项目(LY14A010022);浙江省哲学与社会科学规划资助项目(12JCJJ17YB)

赵晓兵(1968-),男,四川平昌人,浙江财经大学数学与统计学院教授;刘伟(1987-),男,山东泰安人,浙江财经大学数学与统计学院硕士生。

F840.6

A

1004-4892(2015)02-0044-06