动态路径诱导交通阻抗优化方法与实现
李晓丹, 王 浩, 王志平
(1.上海应用技术学院计算机科学与信息工程学院,上海 201418;2.上海瑞纳信息技术有限公司,上海 200433)
动态路径诱导交通阻抗优化方法与实现
李晓丹1, 王 浩1, 王志平2
(1.上海应用技术学院计算机科学与信息工程学院,上海 201418;2.上海瑞纳信息技术有限公司,上海 200433)
基于实时交通采集数据,获取合理动态规划最优路径,提出了考虑驾驶员出行行为因素的交通阻抗优化方法.研究了基于实时交通状态因素的动态路网优先等级指数的确定方法,重构了动态路径诱导交通网络模型,大大降低了路网的复杂度;基于多源实时数据,研究了动态路径诱导交通阻抗优化的计算方法,实现了路网的动态路径诱导,并通过GIS平台进行了仿真分析.该方法更符合驾驶员行为习惯,对于改进Dijkstra算法在动态路径诱导中的应用具有操作优势和显著意义.
交通阻抗;路网优先等级指数;动态路径诱导;Dijkstra算法
动态路径诱导算法是交通诱导系统的核心算法.目前有关路径规划问题的解决方案有很多种,其中以Dijkstra算法最为经典和成熟,是其他许多相关算法设计的理论基础.但这些算法大都存在很高的计算复杂度及较长的计算时间,在动态路径诱导中很难直接使用[1].
Dijkstra算法[2]的主要特点是以起始点为中心向外层层扩展,直至扩展到终点为止.至今,已有不少专家提出了Dijkstra算法的各种改进算法.Sung等[3]在不允许超车行为的前提条件下,给出了一种改进的Dijkstra算法来计算实时路网上的动态最短路;Yu等[4]提出一种新的行程时间网络的模式,依托每一弧段的交通流速度,并证明这种方式是适用于交通网络的;龙琼等[5]基于物理规划的思想,构建了交通阻抗个性化评价指标体系,研究了面向驾驶员“可行性”和“偏好性”需求,基于Dijkstra算法实现了最优路径搜索;刘张雷等[6]改进了前向关联边结构作为路网的存储结构,提高计算时间,考虑交叉口限向和转向延误,对Dijkstra算法进行改进;苏永云等[7]提出将系统工作时间划分为若干时段,给出动态行程时间的计算方法,并进一步研究了基于多车导航的改进Dijkstra算法和基于单车导航的改进A*算法;刘建美等[8]提出将所研究的时间段进行时段划分,然后基于每个路段在每个时段内的历史平均速度给出了改进的Dijkstra算法,它可以给出任意时刻从任意节点位置出发到达任一目的地的行程时间最短的路径及其相应的行程时间,并在允许超车行为存在的条件下将出行者进行分类,并给出了相应的最短路径算法.
以上文献在行程时间计算过程中均未全面考虑道路等级及驾驶员的行为特性.计算出的时间最短或距离最短路径,可能包含了很多低等级道路,或者是在高等级和低等级道路之间频繁切换的路径,这不符合现实中大多数驾驶员的出行习惯.对于驾驶员,时间、速度和舒适才是他们关心的问题.本文研究遵循驾驶员出行行为,假设出行者多数愿意选择其比较熟悉、道路等级较高、连通性能较好的次优路径,而不是单纯的距离最短路径,着重探讨了动态路径诱导中考虑驾驶员行为习惯因素的路网模型重构及交通阻抗的计算方法.
1 路网优先等级指数确定方法
1.1 路网优先等级指数确定
由于驾驶员选择路径的行为因素和交通状态的时变性,城市高等级道路并不总处于优先选择的地位,而城市低等级道路也并不总处于劣势的地位.通常,高等级道路在路径选择算法中具有较高的权重,本文将实时的交通状态因素考虑到道路优先等级再确定过程中,以便给出城市各级道路合理的权重等级.实时交通状态的获取,可根据路段的平均行程车速划分为畅通、拥挤、拥堵3级,具体见文献[9].
依据驾驶员选择路径时通常考虑道路等级而做出优先选择的一般规律[10],将实时交通状态对路网优先等级的影响权重设定为:w=1时为畅通;w= 0.5时为拥挤;w=0时为拥堵.
假设路网优先等级指数G可量化为[1,0.5],分别对应[高层道路,低层道路],则基于交通状态影响权重系数的路网优先等级指数G′可表达为

将式(1)代入量化数据,可得

以当前路网优先等级为高等级道路,加权后路网优先等级指数的确定方法示例:
(1)若当前判断路段为畅通,则新的路网优先等级指数维持不变,即G′=G=1×1=1;
(2)若当前判断路段为拥挤,则新的路网优先等级指数G′=0.5×1=0.5;
(3)若当前判断路段为拥堵,则新的路网优先等级指数G′=0×1=0.
据此,低等级道路加权后新的优先等级指数分别为[0.5,0.25,0].考虑通常驾驶员的选择习惯,可设定路网优先等级指数G′≥0.5的道路加入高层网络.因此,路段交通状态的不同改变了路网优先等级的原始数值.即使高等级的道路,由于其交通状态拥堵,权重降低,路径规划时不可能被优先选择.
按照本节讨论的考虑交通状态影响下的路网优先等级确定方法,可建立如图1所示的对应关系.根据此对应法则,可以获得城市道路的动态路网优先等级,从而可以划分实时的高层网络.
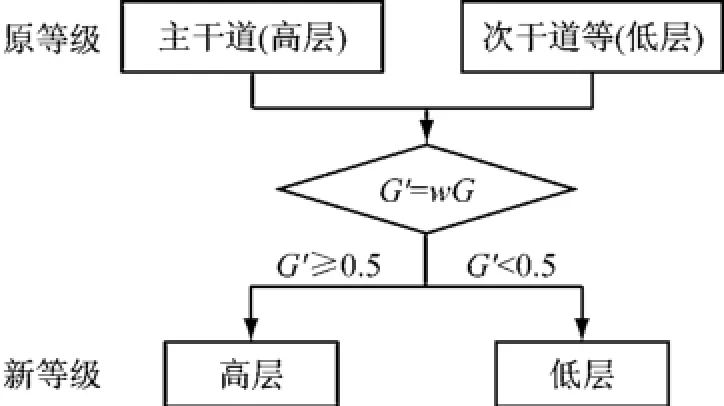
图1 考虑交通状态的路网等级动态分级Fig.1 Dynamic classification of the road network rank by considering traffic state
1.2 城市交通网络模型重构
考虑路段阻抗的交通网络,定义n个交叉口、交叉口间的路段以及路段上交通阻抗,组成交通网络表示路口集;表示与路口相关的路段集,Lij=〈i,j〉表示存在一条从路口i到j的路段;T为阻抗.设路段Lij的阻抗为fij(t1,t2,…,tm),表示从节点i到j的交通阻抗函数.
依据路网优先等级指数,重构交通网络模型,将上游交叉口参数归入路段参数,共同作为交通网络连线的阻抗.其模型示意图如图2所示.

图2 交通网络模型示意图Fig.2 Schematic model of the transport network
2 动态路径诱导交通阻抗优化
获取高层网络模型后,进一步计算该网络中每一路段的阻抗,即可用Dijkstra改进算法搜索行程时间最优路径.
2.1 交通网络交通阻抗优化
浮动车数据(FCD)很大程度上覆盖了整个城市道路,GPS信息可估计路段的行程时间[11].布设在交叉口附近的环形线圈检测器能检测到布设地点的交通流量、占有率和速度等数据,可对交叉口进行停车延误估计.对于交通网络上任意两节点间的平均行程时间,即交通阻抗可表示为

式中:T1为路段平均行程时间;T2为交叉口延误时间.
(1)路段行程时间T1.假设路段平均行程时间的计算间隔为5 min(全文同),则该时段路段上所有车辆的平均行程时间为
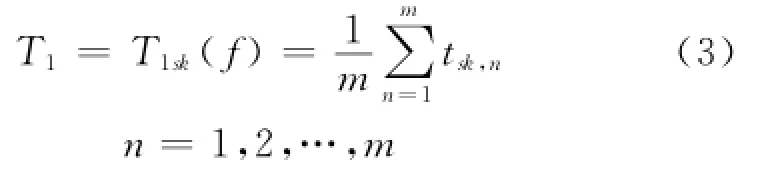
式中:T1sk(f)为在计算间隔s(5 min)内,路段k的平均行程时间;tsk,n为第n辆浮动车在间隔s内,路段k的行程时间;m为在间隔s内通过的浮动车数.
(2)节点延误时间T2.对于交叉口延误的计算,本文根据HCM2000方法,计算公式为

式中:PF为均匀延误修正系数;d1为均匀控制延误;d2为增量延误;d3为初始排队延误.其计算式分别为:


其中:C为信号周期;g为车道组的有效绿灯时长;X为车道组饱和度;c为修正的通行能力;Qb为初始排队长度;μ为延误系数;t为时段T内需求大于通行能力的时间;l为交叉口上游限流修正系数.
2.2 动态最优路径算法
由于动态路径的特点,在路径搜索过程中需按照更新间隔重构交通网络及实时计算出交通网络的交通阻抗,故改进后的Dijkstra算法流程为:首先定义P为永久标号;T为临时标号;S为P标号点的集合;λ为某节点的后向指针的节点,若λ=0,表示该节点为原节点,λ=m,表示不含从原节点到该节点m的路径.
具体流程如图3所示.

图3 动态最优路径算法流程Fig.3 Dynamic optimal path algorithm processes
3 仿真分析
选取某市实际路网的部分区域为例,该区域同时包含浮动车(FCD)数据和检测线圈数据,以ESRI公司ArcGIS 9.3作为二次开发平台,分析交通阻抗优化前后动态路径诱导的对比效果.图4为试验区域的路网,粗线表示高层道路(快速路、主干道),细线表示低层道路(次干道、支路).

图4 试验区域路网Fig.4 Regional trial road network
计算过程中,道路网络交通状态实时计算结果按表1存储在Oracle数据库中,计算的时间区间取2013年9月15日16:30:00~16:35:00,表中列出了部分数据内容.

表1 交通状态参数计算表Tab.1 Traffic state parameter calculation table
图5为优化前计算路径的结果,图6为按照优化算法计算路径的结果.表2列出了2种算法路径搜索结果的部分性能对比.由图5、6和表2可见,优化前计算复杂度较高,所规划出的路径主要在低层网络上,路径长度最短,平均行车速度低,用时长;优化后计算复杂度相对较低,所规划出路径基本都在高层网络上,路径长度稍长,平均行车速度较高,用时短,可提前到达目的地.

图5 优化前计算路径结果Fig.5 Results of computed path before the optimization
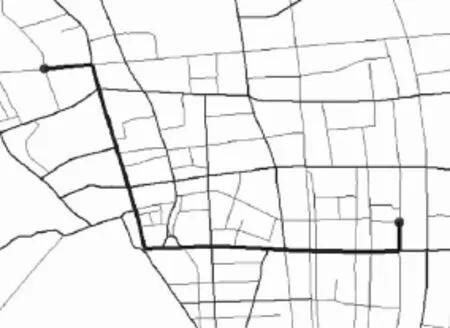
图6 优化后计算路径结果Fig.6 Results of computed path after the optimization

表2 2种算法部分性能对比分析Tab.2 Comparative analysis of performance of the two algorithms

图7 优化前后平均车速和行程时间的对比Fig.7 Comparison between the average speed and travel time before and after the optimization
两种方法的平均车速和行程时间对比如图7所示.利用优化后的路径算法,其规划结果更符合实际诱导系统需求,更能体现驾驶员的选路偏好.
4 结 论
针对城市路网动态路径诱导算法中存在的未能充分考虑道路等级与驾驶员出行行为因素,本文着重解决了以下问题:
(1)根据城市道路原有等级与实时交通状态,提出了交通网络的优先等级指数的确定方法,并重构了算法的交通网络模型,该网络模型可大大缩减算法检索的节点数,提高检索效率及算法效率.
(2)利用城市道路的FCD数据和线圈数据,充分考虑交叉口延误对整体行程时间的影响,优化了路段的交通阻抗即平均行程时间的计算方法;进一步设计了改进的Dijkstra算法,并通过GIS软件对算法进行了验证.
(3)基于改进的交通阻抗优化算法的动态路径诱导,计算复杂度降低,规划路径更符合驾驶员的行为习惯,在实际工程中具有操作优势和现实意义.
[1] 王海梅,周献中.时变道路网最短路径算法的研究[J].火力与指挥控制,2005,30(7):14-17.
[2] 严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,1997.
[3] Sung K,Bell M,Seong M.Shortest paths in a network with time-dependent flow speeds[J].European Journal of Operational Research,2000,121(1):32-39.
[4] Yu Weihui,Chen Hongzhong,Chang Fei.Minimumtime path in network with time-dependent flow speed.[C]//2009 WRI World Congress on Software Engineering.Xiamen,China:IEEE,2009:498-500.
[5] 龙琼,曾革,张谨帆,等.面向驾驶员个性化需求的动态路径诱导方法[J].中南大学学报(自然科学版),2013,44(5):2124-2129.
[6] 刘张雷,史忠科.城市动态时间最短路径诱导系统实现研究[J].控制工程,2010,17(3):351-355.
[7] 苏永云,晏克非,黄翔,等.车辆导航系统的动态最优路径搜索方法研究[J].系统工程,2000,18(4):32-37.
[8] 刘建美,马寿峰,马帅奇.基于改进的Dijkstra算法的动态最短路计算方法[J].系统工程理论与实践,2011,31(6):1153-1157.
[9] 姜桂艳.道路交通状态判别技术与应用[M].北京:人民交通出版社,2004.
[10] 李晓丹.城市道路网络动态优化选择方法研究[J].计算机工程与应用,2014,50(13):243-246.
[11] 李慧兵,杨晓光.面向浮动车取样偏差修正的数据融合方法[J].同济大学学报(自然科学版),2012,40(10):1498-1502.
(编辑 俞红卫)
Traffic lmpedance Optimization Method and Realization for Dynamic Route Guidance
LI Xiaodan1, WANG Hao1, WANG Zhiping2
(1.School of Computer Science and Information Engineering,Shanghai Institute of Technology,Shanghai 201418,China;2.Shanghai Runner Info-Tech Co.,Ltd.,Shanghai 200433,China)
Based on the real-time traffic data collection,a reasonable dynamic optimal path was obtained,and the traffic impedance optimization method was proposed by considering the driver's travel behavior factors.The determining method of the dynamic priority level index of road on the basis of traffic state in real time was studied,and the transportation network model for dynamic route guidance was reconstructed,which led to the significant decline in the complexity of the road network.Based on multisource real-time data,the traffic impedance optimal calculation method of dynamic route guidance was researched.Finally,the realization of the dynamic path of road network was achieved and its simulation analysis was conducted through the GIS platform.This approach was proved to be better fit in with the driver's behavior,and had remarkable significance and operational advantage for the application of the improved Dijkstra algorithm into the dynamic route guidance.
traffic impedance;road priority level index;dynamic route guidance;Dijkstra algorithm
U 491
A
1671-7333(2015)04-0375-05
10.3969/j.issn.1671-7333.2015.04.013
2015-03-04
上海市青年教师培育基金资助项目(ZZyyy13021);上海应用技术学院引进人才基金资助项目(YJ2013-56)
李晓丹(1980-),女,讲师,博士,主要研究方向为交通信息技术与处理、GIS、智能交通系统.E-mail:lxdjiaotong@126.com

