基于样条插值的仿壁虎机器人足端脱附轨迹规划
孙功勋+俞志伟+沈丹妮+吴加明+汪中原+戴振东

摘 要: 针对仿壁虎机器人足端粘附脱附运动,提出了Spline三次样条插值与Matlab/Simulink 半实物仿真相结合的足端轨迹生成及优化的方法。合理选取关键节点,利用三次样条插值,可快速得到所需复杂的光滑轨迹曲线。设计了测试平台并进行半实物仿真,通过分析数据采集卡采集的脱附力的变化趋势,并合理调整三次样条插值数据节点,优化脱附轨迹及其法向力与切向力,使仿壁虎机器人单足脱附过程切向力和法向力保持在较小范围。验证了该方法在单腿运动轨迹生成中的有效性和可行性,为四足步态生成与爬壁实验奠定基础。
关键词: 仿壁虎机器人; 足端轨迹规划; 样条插值; SimMechanics仿真
中图分类号: TN409?34 文献标识码: A 文章编号: 1004?373X(2015)16?0009?04
Conglutination and desorption trajectory planning method for gecko?inspired robot foot?end based on spline interpolation
SUN Gongxun1,2, YU Zhiwei1, SHEN Danni1, WU Jiaming3, WANG Zhongyuan1, DAI Zhendong1
(1. Institute of Bio?inspired Structure and Surface Engineering, NUAA, Nanjing 210016, China;
2. College of Automation Engineering, NUAA, Nanjing 210016, China; 3. Huawei Software Technologies Co., Ltd, Nanjing 210012, China)
Abstract: To plan conglutination and desorption trajectory of gecko?inspired robot, a method to generate and optimize the foot?end trajectory combining cubic spline interpolation with Matlab/Simulink semi?physical simulation is proposed. With proper selection of key node and cubic spline interpolation, the needed complex and smooth trajectory curve can be obtained. A testing platform was designed to carry out the semi?physical simulation. With the analysis on the change trend of the desorption force collected by data acquisition card and reasonable adjustment of cubic spline interpolation data nodes, the desorption trajectory, normal and tangential forces were optimized, which made the normal and tangential forces in the single?foot desorption process of the gecko?inspired robot to be kept in small range. Experimental result shows the reliability and efficiency of this method in the single?leg moving trajectory generation. The optimized trajectory can be applied in the gait planning and wall?climbing of gecko?inspired robot in the future.
Keywords: gecko?inspired robot; foot?end trajectory planning; spline interpolation; SimMechanics simulation
壁虎具有出色的粘附脱附控制能力,它可在墙壁和天花板等各种表面自由攀爬[1],类壁虎机器人在核工业、反恐侦查、航天等领域有很好的应用前景[2]。应用干粘附材料的仿壁虎机器人爬壁时依赖于腿的运动行为,需要一定的预压力使足端干粘附材料与粘附表面达到足够大的接触面积,获得较大的粘附力,而剥落时要尽量减小脱附力[3],因此合理的足端粘附脱附轨迹是仿壁虎机器人进行顺利爬壁的重要因素。
针对干粘附材料的粘附性能测试系统大多是二维测试装置,并且体积较大,性价比较低。此外,现有测试设备没将干粘附材料的粘附性能和仿壁虎机器人的足端粘/脱附轨迹相结合。研究干粘附材料的粘附性能,从而找到应用在机器人足端的粘/脱附轨迹,使仿壁虎机器人拥有较大的粘附力和较小的脱附力,对未来应用于机器人爬壁具有重要理论指导意义和使用价值。
机器人的末端轨迹规划中,足端位姿可用一系列节点表示[4],将机器人的轨迹视为由机器人笛卡尔空间中一系列的关键节点构成[5],可以通过笛卡尔空间所规划的轨迹的运动学逆解得到对应的关节空间角度[6]。笛卡尔空间的轨迹规划相对于关节空间,规划的路径准确,足端的运动轨迹更加直观[7]。但在笛卡尔空间仿壁虎机器人的足端轨迹复杂,不易写出对应的复杂时间和空间函数,而常见形状如直线、抛物线、圆弧等不能满足较理性粘/脱附的要求。文献[8]中,采用相同半径不同圆心的圆弧方程组设计了5种不同脱附轨迹进行脱附,对仿壁虎脚趾的最大脱附力特性进行了测试。该方法生成的圆弧轨迹固定,需要寻找确切的方程来表达,且对运动过程中脱附力特性不理想的轨迹段进行调整优化的灵活性较差。本文提出由Matlab/Simulink搭建含Switch开关模块的单腿轨迹生成与仿真模型,采用Spline样条插值方法将关键节点两两之间通过三次多项式曲线进行连接,并进行轨迹优化,从而得到所需机器人运动的粘附/脱附轨迹。endprint
1 测试平台
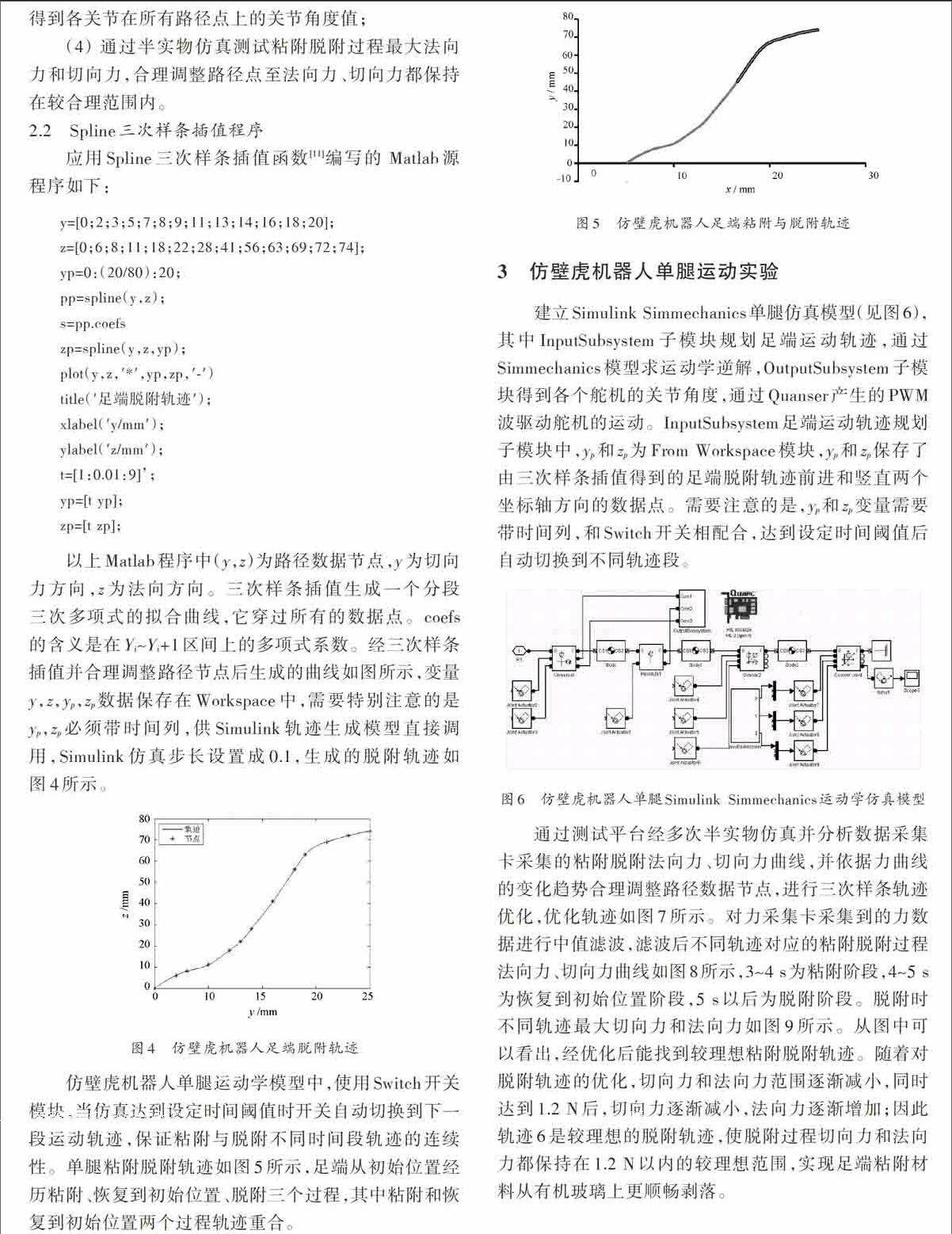
仿壁虎机器人的足端粘附脱附轨迹测试平台如图1所示,机械装置包括力测量和三维运动装置。力测量装置由一个二维力传感器和信号处理设备构成,二维毫牛级H型力传感器与传感器垫片形成悬臂梁结构,通过粘贴有应变片的悬臂梁的形变测量法向力(z方向)和切向力(y方向)。传感器电信号经IBSS数据采集卡采集、放大,最终由YMC9800软件分析、显示、存储,采样频率设置为100 Hz。在传感器顶部安装有机玻璃承重台,运动控制系统中仿壁虎机器人单腿作为运动部件。三个舵机执行三维方向规定轨迹的运动。脚掌由带一定弧度的弹性聚氯乙烯(PVC)材料做基底,干粘附聚氨酯(PU)材料(23 mm×38 mm×2 mm)固定在基底上。
图1 仿壁虎机器人足端粘附脱附轨迹测试平台
由Matlab/Simulink建立步态规划与仿真模型后,通过Quanser进行半实物实时仿真,对力测量与采集装置获得的单腿粘附脱附过程的力数据进行处理与分析。
2 轨迹提取方法
仿壁虎机器人笛卡尔空间的粘附脱附轨迹复杂,常见的直线、抛物线、圆弧等轨迹不能满足有效粘/脱附的要求,因此需要找一种快速可靠的粘附脱附过程数据点生成的方法并对生成的轨迹进行评估、优化。
插值方法中,本文选择具有良好数学特征、易得到平滑曲线的三次样条插值法;插值的实现上;选取了计算功能强的Matlab,能够通过较少的代码实现这一复杂的插值计算。
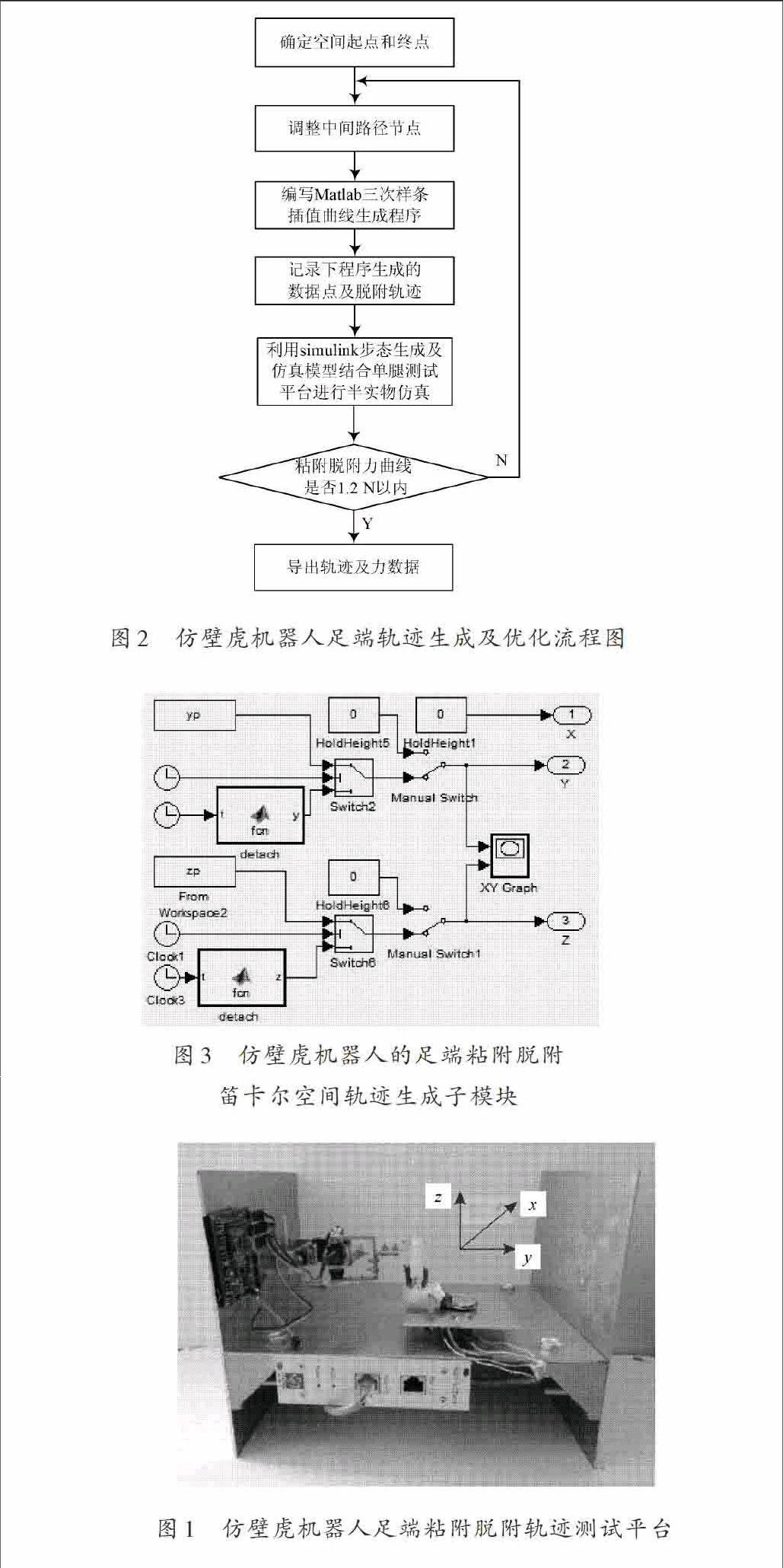
仿壁虎机器人足端轨迹生成及其优化的过程如图2所示。仿壁虎机器人的足端轨迹由粘附和脱附2个过程组成,粘附过程需要脚掌保证足够的接触面积,用直线段就可实现,由Matlab Function模块生成;脱附轨迹由三次样条插值生成,粘附与脱附过程通过Switch开关进行切换。粘附脱附轨迹生成子模块如图3所示。
图2 仿壁虎机器人足端轨迹生成及优化流程图
图3 仿壁虎机器人的足端粘附脱附
笛卡尔空间轨迹生成子模块
2.1 Matlab的Spline样条插值轨迹生成及优化的步骤
(1) 确定足端粘附脱附运动空间起点和终点坐标。在前期脱附过程采用分段抛物线的实验基础上,对实验的脱附轨迹及力趋势进行分析后,设定起止点为(0,0),(20,74),单位为mm,并设置期望经过的中间路径点;
(2) 将各笛卡尔空间坐标值作为三次样条插值轨迹规划算法的输入;
(3) 运用Matlab Spline三次样条插值函数[9?10]编程生成轨迹点,经搭建的Simulink机器人单腿仿真模型,得到各关节在所有路径点上的关节角度值;
(4) 通过半实物仿真测试粘附脱附过程最大法向力和切向力,合理调整路径点至法向力、切向力都保持在较合理范围内。
2.2 Spline三次样条插值程序
应用Spline三次样条插值函数[11]编写的 Matlab源程序如下:
y=[0;2;3;5;7;8;9;11;13;14;16;18;20];
z=[0;6;8;11;18;22;28;41;56;63;69;72;74];
yp=0:(20/80):20;
pp=spline(y,z);
s=pp.coefs
zp=spline(y,z,yp);
plot(y,z,′*′,yp,zp,′?′)
title(′足端脱附轨迹′);
xlabel(′y/mm′);
ylabel(′z/mm′);
t=[1:0.01:9];
yp=[t yp];
zp=[t zp];
以上Matlab程序中(y,z)为路径数据节点,y为切向力方向,z为法向方向。三次样条插值生成一个分段三次多项式的拟合曲线,它穿过所有的数据点。coefs的含义是在Yi~Yi+1区间上的多项式系数。经三次样条插值并合理调整路径节点后生成的曲线如图所示,变量y,z,yp,zp数据保存在Workspace中,需要特别注意的是yp,zp必须带时间列,供Simulink轨迹生成模型直接调用,Simulink仿真步长设置成0.1,生成的脱附轨迹如图4所示。
图4 仿壁虎机器人足端脱附轨迹
仿壁虎机器人单腿运动学模型中,使用Switch开关模块,当仿真达到设定时间阈值时开关自动切换到下一段运动轨迹,保证粘附与脱附不同时间段轨迹的连续性。单腿粘附脱附轨迹如图5所示,足端从初始位置经历粘附、恢复到初始位置、脱附三个过程,其中粘附和恢复到初始位置两个过程轨迹重合。
图5 仿壁虎机器人足端粘附与脱附轨迹
3 仿壁虎机器人单腿运动实验
建立Simulink Simmechanics单腿仿真模型(见图6),其中InputSubsystem子模块规划足端运动轨迹,通过Simmechanics模型求运动学逆解,OutputSubsystem子模块得到各个舵机的关节角度,通过Quanser产生的PWM波驱动舵机的运动。InputSubsystem足端运动轨迹规划子模块中,yp和zp为From Workspace模块,yp和zp保存了由三次样条插值得到的足端脱附轨迹前进和竖直两个坐标轴方向的数据点。需要注意的是,yp和zp变量需要带时间列,和Switch开关相配合,达到设定时间阈值后自动切换到不同轨迹段。
图6 仿壁虎机器人单腿Simulink Simmechanics运动学仿真模型
通过测试平台经多次半实物仿真并分析数据采集卡采集的粘附脱附法向力、切向力曲线,并依据力曲线的变化趋势合理调整路径数据节点,进行三次样条轨迹优化,优化轨迹如图7所示。对力采集卡采集到的力数据进行中值滤波,滤波后不同轨迹对应的粘附脱附过程法向力、切向力曲线如图8所示,3~4 s为粘附阶段,4~5 s为恢复到初始位置阶段,5 s以后为脱附阶段。脱附时不同轨迹最大切向力和法向力如图9所示。从图中可以看出,经优化后能找到较理想粘附脱附轨迹。随着对脱附轨迹的优化,切向力和法向力范围逐渐减小,同时达到1.2 N后,切向力逐渐减小,法向力逐渐增加;因此轨迹6是较理想的脱附轨迹,使脱附过程切向力和法向力都保持在1.2 N以内的较理想范围,实现足端粘附材料从有机玻璃上更顺畅剥落。
图7 足端样条插值脱附优化轨迹
4 结 论
本文对机器人轨迹规划方法进行探讨,通过半实物仿真测试足端粘附和脱附过程中的力学性能,半实物仿真结论如下:Spline三次样条插值方法可以快速生成一系列带时间列的脱附轨迹数据点,通过合理调整路径节点,可优化单腿足端脱附轨迹,使脱附过程中最大法向力与切向力全部保持在较理想范围内。开关模块、Embeded M?fuction模块与三次样条插值轨迹生成方法相结合,可以一次性生成粘附脱附需要的轨迹,在快速得到复杂的脱附轨迹曲线数据点方面具有很大的优势。该方法简单方便,对于仿壁虎机器人轨迹规划具有很高的运用价值。验证了仿壁虎机器人单腿足端轨迹规划方法的正确性和可行性。
图9 足端脱附过程中轨迹最大切向力、
法向力变化曲线
参考文献
[1] YU Z, WANG Z, LIU R, et al. Stable gait planning for a gecko?inspired robot to climb on vertical surface [C]// Proceedings of 2013 IEEE International Conference on Mechatronics and Automation (ICMA). [S.l.]: IEEE, 2013: 307?311.
[2] 方晔,汪小华,梅涛.仿壁虎爬壁机器人的结构及其控制系统研究[J].工业仪表与自动化装置,2009(3):17?19.
[3] WANG Z, DAI Z, YU Z, et al. Optimal attaching and detaching trajectory for bio?inspired climbing robot using dry adhesive [C]// Proceedings of 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). [S.l.]: IEEE, 2014: 990?993.
[4] 王卫忠,赵杰,高永生,等.机器人的平面曲线轨迹规划方法[J].哈尔滨工业大学学报,2008,40(3):389?392.
[5] 李东洁,邱江艳,尤波.一种机器人轨迹规划的优化算法[J].电机与控制学报,2009,13(1):123?127.
[6] 林仕高,刘晓麟,欧元贤.机械手笛卡尔空间轨迹规划研究[J].机械设计与制造,2013(3):49?52.
[7] 任敬轶,孙汉旭.一种新颖的笛卡尔空间轨迹规划方法[J].机器人,2002,24(3):217?221.
[8] 俞志伟,李宏凯,张晓峰,等.仿壁虎脚趾结构设计及粘附运动性能测试[J].机械工程学报,2012,47(21):7?13.
[9] DONG H, ZHAO M, ZHANG J, et al. Gait planning of quadruped robot based on third?order spline interpolation [C]// Proceedings of 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. [S.l.]: IEEE, 2006: 5756?5761.
[10] 王东,陶跃珍.基于Matlab三次样条插值的连杆机构轨迹再现优化设计[J].机械传动,2011,35(1):38?41.
[11] 陈文略,王子羊.三次样条插值在工程拟合中的应用[J].华中师范大学学报:自然科学版,2004,(4): 418?422.

