贴片机贴装路径优化的改进遗传算法

董健腾，龙绪明，曹宏耀，吕文强，胡少华，朱舜文，曾驰鹤

（西南交通大学，四川 成都 610031）

贴片机贴装路径优化的改进遗传算法

董健腾，龙绪明，曹宏耀，吕文强，胡少华，朱舜文，曾驰鹤

（西南交通大学，四川 成都 610031）

贴片机贴装顺序是影响设备生产效率的重要问题，针对此问题，已有各种优化算法提出，包括遗传算法。但是传统的遗传算法（GA）包括一些改进的遗传算法，在解决这个问题上还是存在全局性差、收敛速度慢和易陷入局部最优解的问题。在此基础上加入一个复合算子来优化种群，保证向最优解收敛的同时兼顾种群多样性。配合有效的交叉算子和变异算子，在优化结果上有了更大的改进，能更有效地提高贴装效率。

遗传算法；贴片机；元件贴装顺序优化；复合算子

随着表面组装技术 SMT（Surface Mounted Technology）越来越广泛的应用，电子产品装配较之手工装配发生了质的飞跃，SMT装配线中的关键设备贴片机得到了广泛的关注。为进一步的提高贴片机的性能，其关键因素之一就是提高贴片的效率。对于单台贴片机而言，提高贴片的效率存在两个关键的问题：即贴片机送料器位置分配问题和元件的贴装顺序优化问题。这两者都属于NP-Hard问题，其中后一个问题在单头贴片机情况下一般被规划为旅行商问题 （Traveling Salesman Problem，TSP）［2］。很多学者已经对此提出了各种算法来优化，包括不少遗传算法（GA）［2，3］。但随着贴片机技术的发展，贴片机的结构变得越来越复杂，多头贴片机已成为市场的潮流，其头数已多达12头，甚至更多，结构的复杂化和贴片头的增加使得这些算法不再适用。

本文针对元件的贴装顺序优化问题提出区别于传统遗传算法的改进算法，以解决传统的遗传算法包括一些改进的遗传算法，在解决这个问题上仍存在全局性差、收敛速度慢和易陷入局部最优解的问题。本文通过加入一个复合算子来优化种群，保证向最优解收敛的同时兼顾种群多样性。配合有效的交叉算子和变异算子，来达到优化贴装效率的目的。

1 贴片机原理及数学模型

1.1 贴片机结构和贴装问题描述

贴片机类型多样，型号复杂。按自动化程度分有全自动贴片机、手动贴片机，按工作方式分有动臂式贴片机、转塔式贴片机等，但它们的总体结构均有类似之处，一般贴片机的主要组成部分为：工作台、供料槽，以及用来固定装载元器件的供料器，装载元器件的供料器固定在两边的供料槽上，每个供料器占据一个或多个供料槽，元器件的取贴、旋转等动作都是由装在贴片头上的吸嘴来完成。图1是一种通用转塔式贴片机的内部结构示意图。

贴装工艺：（1）上板和定位：PCB板通过传送带送到指定位置定位夹紧，然后由贴片头上的移动相机对其上的MARK点进行识别，从而得到PCB板的精确位置；（2）取料：贴片头移动到对应的送料器槽位上进行取料；（3）视觉检查：贴片头运动到固定相机上进行视觉检查，判断芯片好坏，并得到元件的偏转角度，距离中心的偏移位置等信息；（4）贴装：根据工艺表和视觉检查信息，贴片头运动到准确的贴装位置进行贴装；（5）抛料：本组贴装完毕后，运动到抛料点位置将视觉检查不合格元件进行抛料；（6）重复第二至第五步骤直到贴装完成；（7）下板：完成所有的贴装点后，松开夹具，通过送板机构将贴装完毕的PCB板送出。

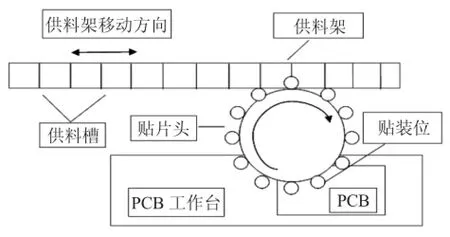
图1 贴片机的内部结构示意图

对于贴片机贴装路径优化问题：已知印制板上各个元器件的装配位置，寻求一个贴片机头遍历这些装配位置的路径，寻求开销最小。该问题与经典的TSP问题有相似之处，属于非对称TSP问题，是遍历整个集合，求最小值问题。不同的是，贴片机贴装要分批进行，如1个4吸嘴的贴片头一个贴装循环内只能贴装4个元器件，一次循环结束后贴片头要返回工料站进行取料再开始下一个循环。

由上面的分析可知，贴片机贴装时间包括：取料时间，贴装时间，循环间吸取原料的时间及弃料抛料时间等。整个贴片机的贴装过程是一个比较复杂的过程，几个问题相互关联，互相影响，很难一次解决，因此大量的研究都是将问题分解成若干个子问题进行研究，先求得局部的最优解，进而得到全局最优解。本文所研究的范围，就是将送料器的位置固定，将元件取贴顺序作为优化的目标。

1.2 数学模型

基于上一节的描述，本文参照文献［4，5］做以下假设：（1）假设供料器位置为原点；（2）将不影响问题本质的贴装头的旋转时间忽略；（3）假设吸嘴吸片时间固定，贴片时间固定。故一个完整的贴装时间可以表示为：

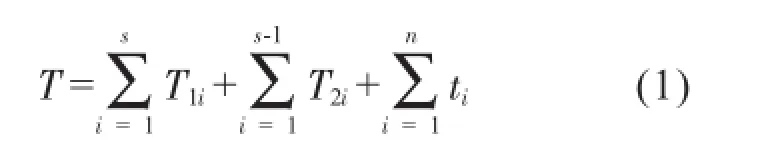
式中，表示第i个循环内贴片头总移动时间，表示贴片头从第i个循环的最后一个元件贴装完毕到移动至下一个循环的第一个元件的贴装位置所需时间，ti表示第i个元件的贴片时间。在上文中已经提到，假设每个元件的贴片时间一定，故第三个参数不影响贴装路径优化。s表示总循环次数，n表示总元件个数。贴片机贴片运动按距离远近，x、y方向的运动有加速-减速（短距离）、加速-恒速-减速（长距离）两种形式。如果设定运动距离为S、加速度为a、恒速度为v可得到对应的运动时间t的计算公式：

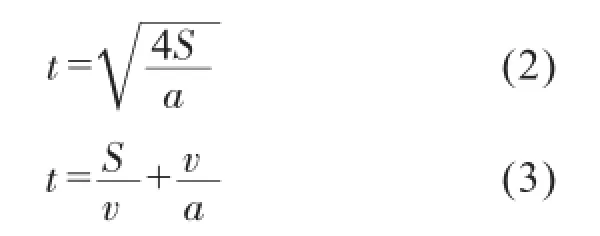
式（2）为短距离时间，式（3）为长距离时间，因为v、a都是固定参数的设定值。故根据公式（1）和公式（2）、（3）求贴装时间的最小值便可以简化为求式（4）的最小值，即：

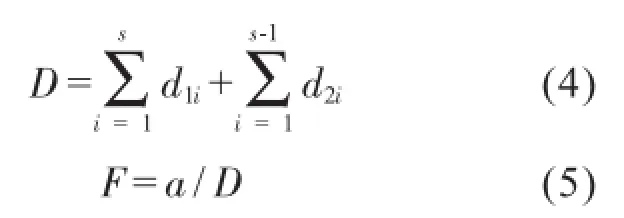
式（5）中a为固定标度转换参数）

式（4）中d1表示贴装循环内贴片头要移动的距离，d2表示循环间贴片头要移动的距离。距离的计算采用欧式距离，根据公式（4）可知，遗传算法的适应度函数可参考公式（5），即对公式F最大值的寻优。

2 研究现状与算法介绍

2.1 研究现状

对于贴片机的贴装顺序优化问题，已经有很多学者做了研究，提出多种算法来解决，包括遗传算法、蚁群算法、伞布搜索法、差分算法、模拟退火算法、启发式算法等。

国外研究成果较多，比如 M.o.Ball和MJ. Magazine［10］提出了一种类似“邮递员”问题的优化算法对单吸头、电路板和供料器静止的贴片机贴装顺序进行优化；Nevalainen［11］提出将整个优化问题可以分成两个子问题，使用二次分配问题来解决供料器的分配问题，用非对称旅行商问题来解决贴放顺序问题；Edmund.K.Burke等人［13］提出一种整体模型使用启发式算法对多头拱架式贴片机进行优化研究。国内对此研究起步较晚，比如袁鹏等人［13］使用伞布搜索算法分别在元器件供料器位置固定的情况下，对多吸嘴拱架式贴片机进行优化研究；杜轩等人［14］使用遗传算法在贴片顺序确定的情况下进行供料器的分配优化研究；田福厚等人［15］使用遗传算法对转塔式贴片机贴装过程进行优化研究。

贴片机上的优化问题属于复杂的组合优化问题，从己有的数学模型来看都属于NP-hard问题。随着贴片机本身的结构和性能在不断的更新和改进，人们也在探索新的方法来得到更好的结果。

2.2 遗传算法

遗传算法是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机智能搜索方法。遗传算法在群体进化过程中发生繁殖、杂交和突变现象，不断发现重要基因。寻找较好模式的过程中，高适应度的个体被选择的概率大于低适应度的个体，则好的基因得以遗传下来，不好的基因被剔除，经过若干代之后，算法收敛于最好的染色体，它很可能就是问题的最优解或次优解。算法主要包括3部分：多样性初始种群的产生，种群的优化更新（其中的算子包括复制算子、交叉算子和变异算子），最优个体的出现。

在对贴片机贴装顺序优化的应用中，遗传算法展现出了优势，但传统的遗传算法在全局性和收敛速度上都存在缺点，而且贴片机高速发展，现在需要更有效率的算法，本文提出了一种有效的改进算法。

3 改进遗传算法

3.1 复合算子

遗传算法简单通用，具有很强的全局搜索能力，但是，大量的实践数据表明，遗传算法在优化过程中局部搜索能力差，容易陷入早熟收敛，群体的多样性急剧降低，导致个体之间的竞争力度大大降低，群体的进化能力基本丧失。其表现就是遗传算法往往收敛不到全局最优解。为此本文提出改进遗传算法流程图，见图2所示。

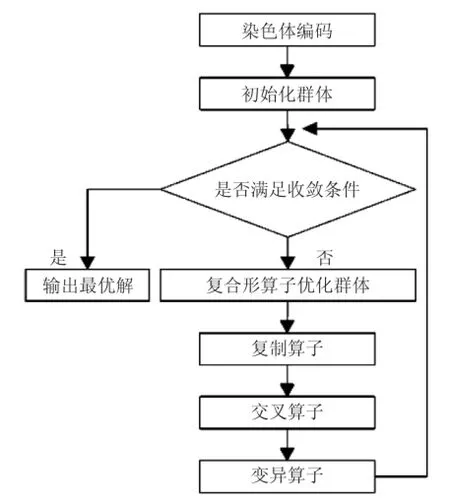
图2 改进遗传算法流程图

为了使遗传算法具有快速局部寻优能力，对其进行改进优化，我们必须解决两个关键问题：（1）保证最优解的搜索方向；（2）维持群体的多样性。我们提出的改进遗传算法的思路就是将复合算子，融入到遗传算法中，起到引导群体搜索方向，改善群体多样性的作用。

复合算子的设计思路源自文献［3］，它将贴装优化过程简化成一个非对称的TSP问题，提出用单亲进化遗传算法（PEGA）解决问题。主体思路是尽可能的利用父染色体中基因片段的信息，将贴片间距大于某一阈值的基因串打断，由此将个体分成一个个的子串，保留优秀子串。但是该算法亦存在种群多样性差，易陷入局部解的问题。本文在它的基础上提出复合算子，步骤如下：

步骤一：以10个元件为例，计算种群中每一个个体的适应度函数，并进行排序；

步骤二：挑出适应度较高的一半个体，比如其中一个个体为：

F为2 4 5 9 6 1 3 7 8 0，贴片移动距离di为（2，4），（4，5），（5，9），（9，6），（6，1），（1，3），（3，7），（7，8），（8，0）；

步骤三：计算这一半个体di的均值并设定为阈值；

步骤四：在另一半个体中根据阈值进行过滤，统计di大于阈值的次数，超过设定个数则淘汰之；

步骤五：用高适应度个体通过反射函数，在约束条件确定的可行域内形成N个新个体，替换掉原来被淘汰掉的N个个体。

该算子在优化问题中，就是通过不断产生靠近最优个体的优良个体来代替当前群体中的最差个体，达到不断改善群体结构，加速收敛进程的目的，这与遗传算法核心理念是一致的。

3.2 复制算子

遗传算法中通过个体的适应度来对群体中个体的好坏程度进行评判，复制算子把当前群体中的个体按照与适应度成比例的概率复制到新的群体中。本文采用经典的轮盘赌选择方法：每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度之和的比例，适应度值越高，进入下一代的概率就越大。

3.3 交叉算子

生物的进化中，父代根据基因交配进行遗传信息的重组，诞生子代。交叉算子是依据较大的概率从群体中选择两个父代，交换两个个体之间的某个或某些基因位，继承父代的基本特征。遗传算法的收敛性主要取决于交叉算子的收敛性［9］。

在此采用一种高效的交叉算子，使最优解出现的更快，算法效率更高。操作过程如下：

（1）对种群个体两两组合形成父代双亲。

（2）随机产生一个交叉点P，并在交叉点到最后节点之间产生一个随机数S。

（3）分别把双亲中每个个体自交叉点后的S个基因位按照原序列放在另一个体前面，后依次删去重复的基因位，如此产生出子代。

如父代双亲为：

P1=［8，7，2，6，5，1，9，10，3，4］

P2=［2，4，6，5，9，10，1，3，8，7］

若随机产生P=2，S=3，

则步骤2之后

P1'=［6，5，9，8，7，2，6，5，1，9，10，3，4］

P2'=［2，6，5，2，4，6，5，9，10，1，3，8，7］

删去重复基因得到新的子代个体：

P1=［6，5，9，8，7，2，1，10，3，4］

P2=［2，6，5，4，9，10，1，3，8，7］

比较两个父代和子代的适应度，选择适应度最大的留下来，作为最终的子代个体。这样保证了每次都遗传最好的基因，加快了最优解出现的速度。

3.4 变异算子

变异算子是以较小概率，一般为0.001至0.1，对个体某些基因位进行改变，传统的二进制编码是通过“0”、“1”互换方式产生新个体。但本课题中元件染色体上的基因不再是非0即1的二元结果，而是随元件贴装点的个数变化的某一区间。依据上文双点交叉算子的思想，我们提出了基于单点的基因位对称变异算子。假设：设贴装总数为N，变异基因位为i，M代表某一位基因位，选择某个体进行变异操作。

（1）随机产生位于［1，N］的基因突变位，假设变异位为i；

（2）若个体基因位为偶数时，交换Mi与MN+1-i两个位置上的基因；

（3）若个体基因位为基数时，除基因位i= （N+1）/2的基因不发生改变，其他情况交换Mi与MN+1-i两个位置上的基因；

假设N=10，i=5。

个体变异前的基因序列：

8-＞7-＞2-＞6-＞5-＞9-＞3-＞1-＞10-＞4

个体变异后的基因列：

8-＞7-＞2-＞6-＞9-＞5-＞3-＞1-＞10-＞4

通过对种群进行单点基因位对称变异，从局部的角度进行优化搜索，最终向整体最优解收敛。

4 实 验

实验以一个拥有20个元器件的PCB板为例，其中PCB板的尺寸为200 mm×100 mm，供料器坐标位置为（0，0），各个元件的坐标如表1所示。

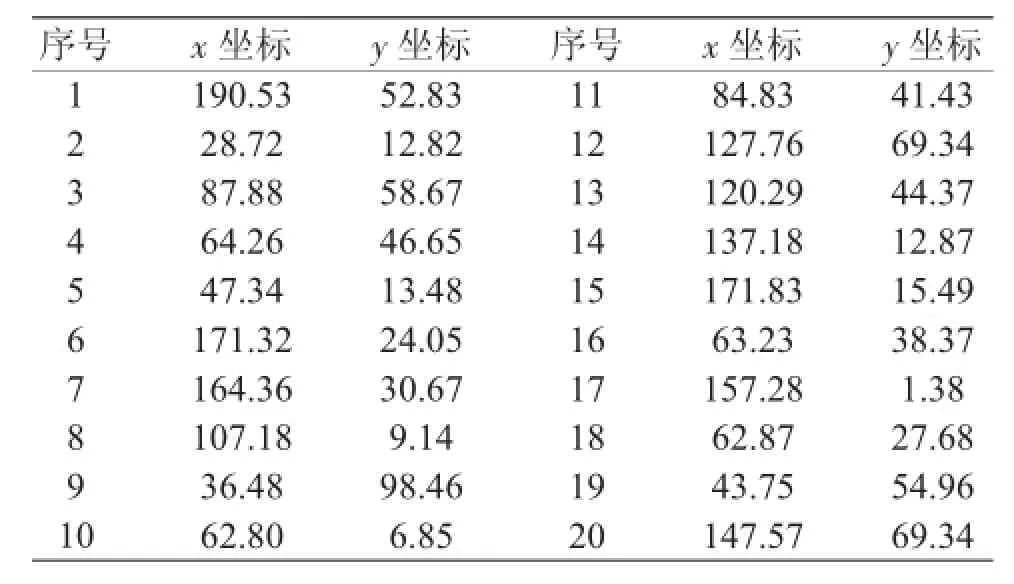
表1 元器件坐标mm

设定初始种群大小为30，迭代次数为300，交叉概率为0.9，变异概率为0.01，则采用传统遗传算法、单亲进化遗传算法和本文提出的改进遗传算法的优化过程对比图分别如图3和图4所示。

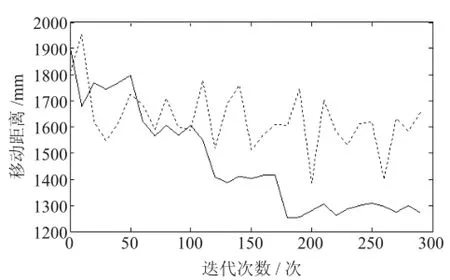
图3 传统遗传算法和本文算法优化过程图（实线为改进遗传算法）

从图3不难看出，传统遗传算法在解决贴片机贴装路径优化上效果并不是很好，算法收敛速度慢，全局性差，难以达到最优解。从图4可以看出，单亲进化遗传算法虽然有比较好的收敛速度和全局性，但是因为对父代种群选择的过度优化，导致收敛过快，影响全局性，陷入局部最优解的困境，而难以达到全局最优解。

Application of Improved Genetic Algorithm in Optimization of Placement Path of Placement Machine

DONG Jianteng，LONG Xuming，CAO Hongyao，LV Wenqiang，HU Shaohua，ZHU Shunwen，ZENG Chihe
（College of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China）

The sequence of placement has a great influence to the efficiency of the placement machine. In view of this problem，there are various optimization algorithms，including genetic algorithm mentioned in this paper.But the traditional genetic algorithm （GA），including some improved genetic algorithm，in the solution of the problem or the existence of the global poor，slow convergence speed and easy to fall into local optimal solution.In this paper，a composite operator is added to optimize the population，which is guaranteed to converge to the optimal solution.With the effective crossover operator and mutation operator，the optimization results and the efficiency of mounting have a greater improvement.

Genetic algorithm；Chip mounter；Component placement sequence optimization；Complex operator

TN605

A

1004-4507（2015）12-0017-06

2015-11-19