基于不确定理论的光伏出力预测研究

赵书强 王明雨 胡永强 刘晨亮

（华北电力大学新能源电力系统国家重点实验室 北京 102206）

0 引言

随着新能源的发展，太阳能受到广泛关注，大规模光伏并网发电成为太阳能发电的发展趋势[1]。光伏发电受到地理位置、物理环境和气象条件等因素的影响，其中，太阳辐射值和温度是最主要的因素[2]。各种因素的波动性使光伏发电的功率也具有不确定性。所以，有必要对光伏出力进行预测，这有助于电力系统调度部门合理制定调度计划，及时调整出力分配[3]。

对光伏出力的预测方式有两种：直接和间接预测。直接预测是直接得到光伏出力；间接预测是通过预测太阳辐射值得到出力。对太阳辐射的预测分为两种：物理法和统计法。物理法是利用现有物理模型，直接将气象数据作为输入，代入公式即得到预测值。比较完善的有晴天ASHRAE模型[4]、HOTTEL模型[5]、REST模型[6]、有云天气 Nielsen模型及云遮系数模型[7]等。统计法是利用某种统计方法，如回归模型、灰色预测、神经网络等，对历史数据进行分析，寻找数据中的内在规律并用于预测。如文献[8,9]采用支持向量机的方法，但输入只有温度，没有充分考虑气象因素的波动性，因此不具有普适性。神经网络一般是按照季节、日类型建立子模型[10-12]，选取部分气象因素作为输入，但只考虑了确定性因素，忽略了随机性因素。还有一些方法将神经网络与其他智能方法相结合，文献[13]先对数值天气预报的数据进行模糊识别，文献[14]将小波变换与模糊神经网络结合，但模糊系统中模糊推理规则的建立需要大量的历史数据和充足的专家经验。

本文以不确定理论为基础，利用双重随机理论计算不同预测云量对应的云遮系数期望值和关键值，得到不同置信水平下的云遮系数区间。再以无云天气下计算太阳辐射值的REST模型为基础，用云遮系数对其进行修正，得到不同预测云量下的太阳辐射值。然后根据出力模型，最终得到光伏出力的预测值。

1 双重随机理论

工程问题中存在很多不确定信息，不确定理论[15]是研究不确定信息的重要方法，文献[16]建立了不确定理论的公理化体系，成为研究不确定信息的实用途径。

1.1 双重随机变量

定义1如果ξ是从概率空间（Ω,A,Pr）到随机变量集合的函数，则ξ是双重随机变量。其实ξ就是一个取值于随机变量集合上的随机变量。

定义2设ξ是双重随机变量，如果下式右端两个积分中至少有一个为有限，则

式中，E(ξ)为双重随机变量ξ的期望值。

定义3设ξ是双重随机变量，α,β∈(0,1]，则称

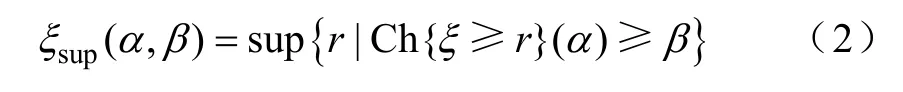
为ξ的（α,β）乐观值，而称

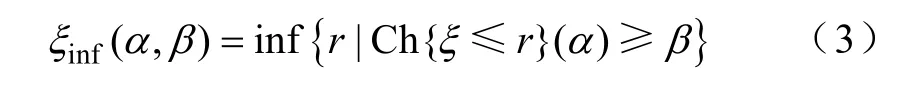
为ξ的（α,β）悲观值。

乐观值和悲观值是度量双重随机变量的两类关键值。

定义4双重随机变量ξ的机会测度定义为

1.2 双重随机模拟算法

（1）算法1：随机模拟算法（求随机变量的期望值）。

1）令L=0。

2）根据概率测度Pr，从Ω中抽取样本ω。

3）L←L+E[f(ξ(ω))]。

4）重复步骤2）、3）共N次。

5）E[f(ξ)]←L/N。

（2）算法2：双重随机模拟算法（求双重随机变量的期望值）。

1）令e=0。

2）根据概率测度 Pr，从样本空间Ω中抽取样本ω。

3）e←e+E[f(ξ(ω))]，其中E[f(ξ(ω))]可以通过随机模拟得到。

4）重复步骤2）、3）共N次。

5）E[f(ξ)]←e/N。

（3）算法3：双重随机模拟算法（求双重随机变量的乐观值）。

1）根据概率测度Pr，从样本空间Ω中随机产生样本ω1,ω2,…,ωN。

3）置N'为αN的整数部分。

计算悲观值的算法与乐观值类似。

2 太阳辐射值的预测模型

太阳辐射可以分为直接辐射和散射辐射。辐射值在传输过程中会受到很多因素的影响，如云的反射和散射[17]。下面分别对无云和有云天气的辐射预测进行建模。

2.1 无云天气太阳辐射值的计算模型

本文采用REST模型计算晴天的直接辐射和散射辐射。将2006～2011年每年12月晴天的辐射值作为历史数据，其中2009年的结果如图1所示，其中横坐标为整点为晴天的时刻的累计数量，纵坐标为各时刻对应的辐射值。可以看出，直接辐射的计算值与实际值误差很小，散射辐射的计算值与实际值变化趋势一致，但有一定差距，原因是REST模型中的参数存在季节性或地区性差异，因此采用一次函数对其进行拟合，即

式中，Idif为REST模型得到的散射辐射；Idif1为拟合修正后的散射辐射；k、a为修正系数。

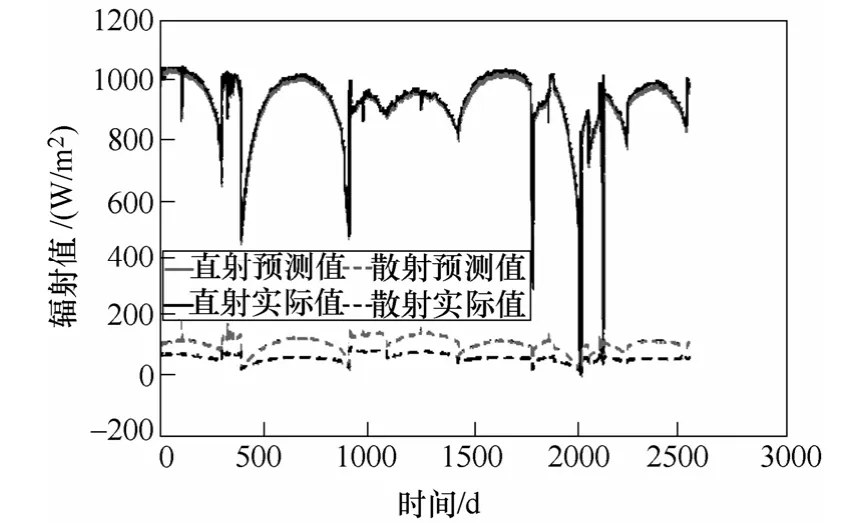
图1 直射与散射计算值与实际值的对比Fig.1 The comparison of calculated value and actual value of direct and scattered radiation

将历史散射值与计算值进行线性拟合，得到修正的散射值计算公式为

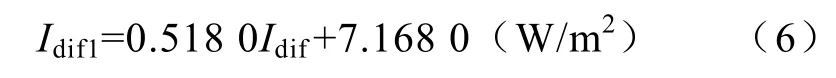
修正后的结果如图2所示，从图中可以看出，修正后的散射值比修正前更接近实际值。

图2 修正前后散射辐射值与实际值的对比Fig.2 The comparison of predicted scattered radiation value before and after correction with the actual value

2.2 有云天气太阳辐射值的计算模型

云的形状、高度、厚度是不断变化的，因此对太阳辐射产生的效应也会具有不确定性[18]，在对太阳辐射值预测时，云量是要重点考虑的因素。云对直射和散射的影响方式不同，需要分别进行分析。目前对有云天气太阳辐射值的预测，多采用与云量有关的函数对无云天气的辐射值进行校正，本文采用云遮系数模型，即

式中，Ic为有云天气的辐射值；I0为REST模型计算的无云天气辐射值；ξ为对应云遮系数。

2.2.1云量的模糊性

对云的描述通常有云量和云层覆盖率两种。云量是云对天空遮蔽的成数，用成数Ci(i∈(0,1,…,10))表示，我国采用 10成制。云层覆盖率z(z∈(0,1,…,100))用云占天空的百分比表示。

云量具有模糊性，人们认识上的差异会导致对云量的定义不同。对云量的划分不是一个确定的点，而是具有一定交集的区间。选取三角隶属函数μCi计算各个云层覆盖率z对云量Ci的隶属程度μ，具体划分如图3所示。

图3 云层覆盖率对云量的隶属函数图Fig.3 Membership function of cloudiness cover percentage to cloud cover

每个时刻的云量用隶属度向量F(zk)=(μC0(zk),μC1(zk),μCi(zk),μC10(zk))表示，其中μCi(zk)为云层覆盖率zk(k=1,2,…,n)对云量Ci(i=0,1,…,10)的隶属度。这样，根据可信性理论，每个云量Ci对应一个可能性空间(z,p(z),μCi(z))。

2.2.2云量的随机性

云量具有随机性，若预报的云量为Ci，实际出现的云量可能为0～10之间的任意值，各个值的概率可以通过如下步骤得到。

（1）云量预测值采用美国国家海洋和大气管理局（NOAA）提供的数据，统计研究时段内预测云量为Ci(i=0,1,…,10)的数量Ni。对Ni的统计采用直接计数方法，即有一个云量为Ci的时刻Ni就加1。

（2）在历史数据中，统计云量预测值为Ci时实际值为Cj的数量。由于实际云量是用隶属度向量表示，所以计数方法也与一般情况不同。

式中，yk为第k个预测云量；sk为第k个实际云层覆盖率；μCi(yk)表示预测云量对Ci的隶属度，此处取值为1；μCj(sk)表示实际云层覆盖率对Cj的隶属度。

（3）预测云量为Ci的情况下实际值为Cj的概率为

由上式可知，从预测云量Ci到实际云量Cj对应一个随机变量集合。

2.2.3云遮系数的随机性

云遮系数具有随机性。通过对历史数据的统计，直射和散射云遮系数的取值范围分别是ξ1k∈[0,1]和ξ2k∈[−5,1]，可以统计得到其概率分布，步骤如下：

（1）确定历史数据，采用 2006～2011年每年12月的数据，利用REST修正模型，得到无云天气太阳辐射的计算值，根据式（7）分别计算各个时刻的直射和散射云遮系数，散射云遮系数的计算值如图4所示。可以看出，同一云层覆盖率下的云遮系数不是一个确定的值，而是具有离散的概率分布，这样实际云量对应的云遮系数就是随机分布的。

（2）统计历史数据中实际云量为Cj(j=0,1,…,10)的数量为

图4 散射云遮系数的随机性Fig.4 Probability of cloud cover coefficient corresponding to diffuse irradiation

式中，sm为第m个实际云层覆盖率；μCj(sm)表示sm对云量Cj的隶属度。

（3）将直射和散射云遮系数按照数值大小分别平均分为n1=50和n2=100个区间，并统计云量实际值为Cj时直射和散射云遮系数落入各个区间的数量(k=1,2,…,n1)和(k=1,2,…,n2)，即

也就是说，如果第m个时刻的直射云遮系数ξ1m落在第k个区间内，则数量要加上该时刻的云层覆盖率sm对云量Cj的隶属度。

由上可知，实际云量Cj对应的云遮系数ξjk也是一个随机变量集合。

2.2.4有云天气辐射值的预测

由上述分析可知，预测云量Ci对应的实际云量Cj是随机变量，实际云量Cj对应的云遮系数ξjk也是随机变量，因此预测云量Ci对应的云遮系数ξik是取值于随机变量集合上的随机变量，具有双重随机性[19]，表达式为

预测流程如图5所示，具体步骤如下：

（1）对云量进行模糊划分，得到云层覆盖率对应的云量实际值，即云量隶属度向量F(zk)，对比同一时刻的云量预测值和云量实际值，统计得到云量预测值到实际值的随机概率分布Pij。

（2）计算历史数据中各个时刻的云遮系数ξ1k和ξ2k，得到云量实际值为Cj时云遮系数的随机概率分布P1jk和P2jk。

（3）采用双重随机模拟算法计算各个预测云量对应的云遮系数期望值，以及满足不同置信水平的云遮系数区间。

（4）利用REST模型计算晴天的太阳辐射值，然后根据云量预测值，选取相应的云遮系数期望值对其进行修正，最终得到有云天气的辐射值。

图5 预测流程图Fig.5 Forecast flowchart

3 温度和光伏出力的预测模型

温度是光伏出力的另一个重要影响因素，本文用 BP神经网络模型预测光伏电池的温度。通过对各个环境因素与光伏电池温度的相关性分析得知，光伏电池温度与环境温度和光伏电池接收的辐射值相关性最强。因此，将环境温度和辐射值作为神经网络的输入，光伏电池的温度作为输出。步骤如下：首先利用历史数据对神经网络模型进行训练，训练次数为1 000次；然后输入预测日的环境温度预报值和第2节根据双重随机模型所得到的太阳辐射期望值，即可得到光伏电池温度的预测值。

光伏电池出力的简化计算模型[20]如式（14），由于最大功率追踪装置的作用，可以计算任意光强和温度下光伏电池的最大输出功率。

式中，Tref、Sref为光伏电池温度和太阳辐射参考值，分别为25℃、1 000W/m2；ΔT、ΔS为实际的电池温度和太阳辐射与参考值的差；Pm为标准条件下，光伏电池的最大输出功率，本文算例中光伏系统容量为1kW，所以Pm取1 000W；a、b、c为补偿系数，分别为0.002 5℃−1、0.000 5W/m2和 0.002 88℃−1。

4 算例分析

本文利用美国 BMS光伏电站的数据来验证模型的有效性，有效光照时间为每天的8:00～16:00。以2012年12月11日为例，先提前一天预测整点时刻的直接辐射Idir和散射辐射值Idif，再预测光伏电池的温度值，然后根据光伏出力模型计算出力。

4.1 期望值预测

图6 2012年12月11日太阳辐射预测期望值与实际值的对比Fig.6 Comparison of predicted solar radiation expectations with the actual valueon December 11th,2012

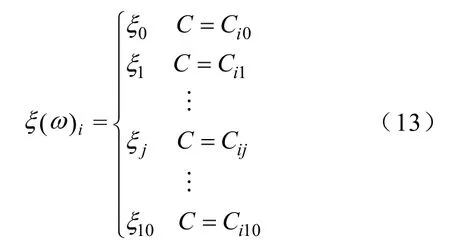
太阳辐射的期望值预测结果如图6所示，相应的光伏出力预测结果如图7所示。直接辐射、散射辐射和总辐射预测值的平均相对误差分别为26.88%、15.13%和 21.55%；对光伏出力预测的平均相对误差水平在15%左右。

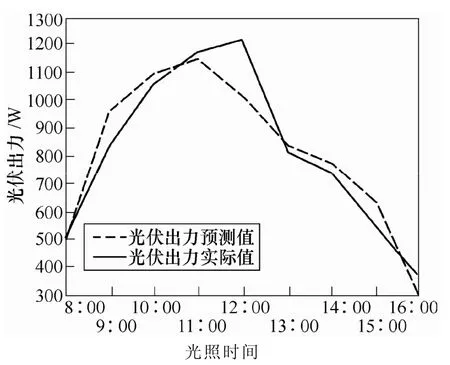
图7 2012年12月11日光伏出力预测期望值与实际值的对比Fig.7 Comparison of predicted PV output expectations with the actual valueon December 11th,2012

4.2 区间预测

太阳辐射的置信水平为[0.6,0.7]的关键值预测结果如图 8所示，相应的光伏出力预测结果如图 9所示。

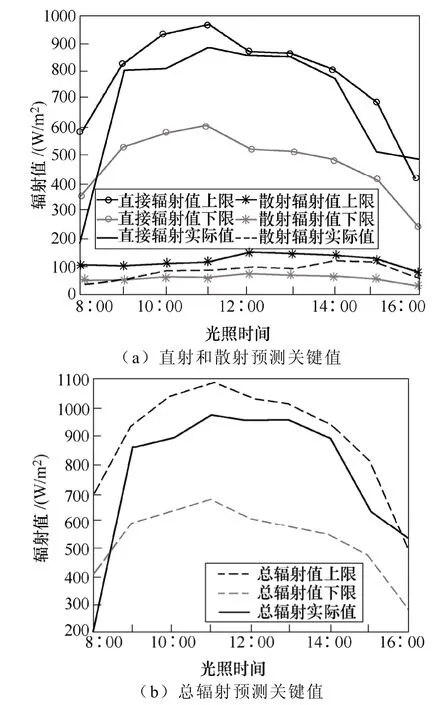
图8 2012年12月11日太阳辐射预测关键值与实际值的对比Fig.8 Comparison of predicted solar radiation critical values with the actual value on December 11th,2012

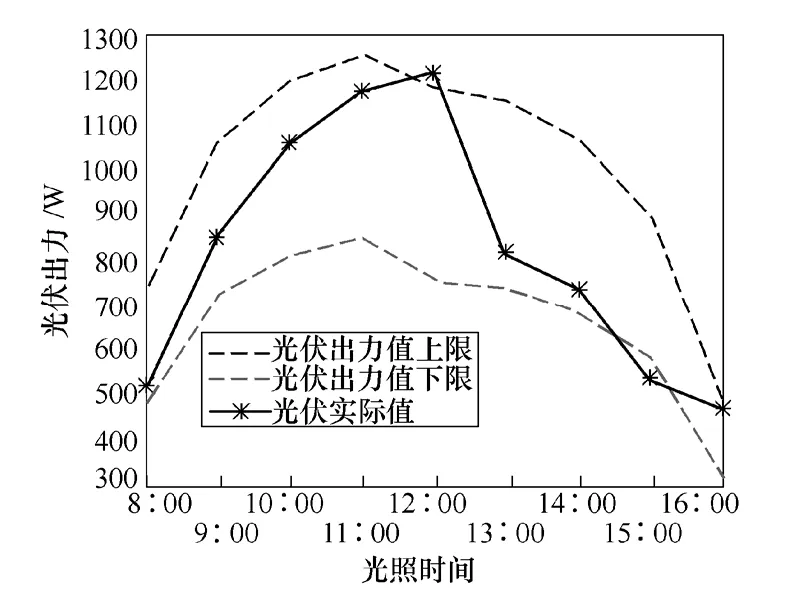
图9 2012年12月11日光伏出力预测关键值与实际值的对比Fig.9 Comparison of predicted PV outputcritical values with the actual value on December 11th,2012

双重随机模拟算法可以预测得到辐射值的预测区间，可以看出，大部分辐射实际值包含在预测区间上限和下限之间，8:00和16:00的实际值没有在区间内，原因是在早晨太阳刚升起和下午太阳即将落下的时候，辐射值受水蒸气和空气污染物的影响较大，不规律性较强。对光伏出力来说，由于还受到温度的影响，8:00和16:00的实际值没有落在区间外部。通过研究不同置信水平下太阳辐射值的预测结果，得出如下结论：随着置信水平的增大，预测区间变大，更多的实际值落在区间内；反之，落在区间内的实际值变少。当α不变，β减小时，或者当β不变，α减小时，预测区间都变小，落在区间内的实际值也减小。

模型实现了提前一天对光伏出力的短期预测，预测准确度受天气预报准确度的影响。考虑到天气会出现瞬时多变或突变情况，还需要加入滚动预测，即根据天气情况实时调整预测值。将基于不确定理论的模型与滚动预测相结合，能够提高光伏出力预测的准确度，这是本文未涉及的内容，还有待进一步研究。

5 结论

预测光伏出力可以为电力系统调度部门提供重要的参考信息。本文建立了基于不确定理论的太阳辐射值预测模型，是一种新型预测方法。文中分析了云量的随机性和云遮系数双重随机性，并考虑了云量的模糊性，较全面地涵盖了辐射值影响因素的不确定性。在实现太阳辐射值和光伏电池温度的预测后，通过光伏出力的工程实用模型得到出力的预测值和预测区间，与只能得到单一预测值的传统方法相比，预测结果的信息量更加丰富，更具有参考价值。

[1] 王飞,余世杰,苏建徽,等.太阳能光伏并网发电系统的研究[J].电工技术学报,2005,20(5):72-74.

Wang Fei,Yu Shijie,Su Jianhui,et al.Research on photovoltaic grid-connected power system[J].Transactions of China Electrotechnical Society,2005,20(5):72-74.

[2] 蒋亚娟.光伏电池建模及其在光伏发电预测中的应用[D].武汉:华中科技大学,2011.

[3] GablerH.Grid-connected photovoltaics[J].Solar Energy,2001,70(6):455-456.

[4] 后尚,田瑞,闫素英.呼和浩特地区太阳辐射模型分析[J].可再生能源,2008,26(2):79-82.

Hou Shang,Tian Rui,Yan Suying.Research and analysis on the solar radiation model of Huhehaote[J].Renewable Energy Resources,2008,26(2):79-82.

[5] 邱国全,夏艳君,杨鸿毅.晴天太阳辐射模型的优化计算[J].太阳能学报,2001,22(4):456-460.

QiuGuoquan,Xia Yanjun,Yang Hongyi.An optimized clear-day solar radiation model[J].Acta Energiae Solaris Sinica,2001,22(4):456-460.

[6] Shah Alam.Prediction of direct and global solar irradiance using broadband models:validation of REST model[J].Renewable Energy,2006,31:1253-1263.

[7] 李小芳,陈青云.用云遮系数法计算日光温室内太阳辐射[J].农业工程学报,2004,20(3):212-216.

Li Xiaofang,Chen Qingyun.Calculation of the solar radiation inside the sunlight greenhouse using the cloud cover coefficient method[J].Transactions of The Chinese Society of Agricultural Engineering,2004,20(3):212-216.

[8] 栗然,李广敏.基于支持向量机回归的光伏发电出力预测[J].中国电力,2008,41(2):74-78.

Li Ran,Li Guangmin.Photovoltaic power generation output forecasting based on support vector machine regression technique[J].Electric Power,2008,41(2):74-78.

[9] 傅美平,马红伟,毛建容.基于相似日和最小二乘支持向量机的光伏发电短期预测[J].电力系统保护与控制,2012,40(16):65-69.

Fu Meiping,Ma Hongwei,Mao Jianrong.Short-term photovoltaic power forecasting based on similar days and least square support vector machine[J].Power System Protection and Control,2012,40(16):65-69.

[10] 陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的研究[J].电工技术学报,2009,24(9):153-158.

Chen Changsong,Duan Shanxu,Yin Jinjun.Design of photovoltaic array power forecasting model based on neutral network[J].Transactions of China Electrotechnical Society,2009,24(9):153-158.

[11] 丁明,王磊,毕锐.基于改进BP神经网络的光伏发电系统输出功率短期预测模型[J].电力系统保护与控制,2012,40(11):93-99.

Ding Ming,Wang Lei,Bi Rui.A short-term prediction model to forecast output power of photovoltaic system based on improved BP neutral network[J].Power System Protection and Control,2012,40(11):93-99.

[12] 张艳霞,赵杰.基于反馈型神经网络的光伏系统发电功率预测[J].电力系统保护与控制,2011,39(15):96-101.

Zhang Yanxia,Zhao Jie.Application of recurrent neutral networks to generated power forecasting for photovoltaic system [J].Power System Protection and Control,2011,39(15):96-101.

[13] 陈昌松,段善旭,蔡涛,等.基于模糊识别的光伏发电短期预测系统[J].电工技术学报,2011,26(7):83-89.

Chen Changsong,Duan Shanxu,Cai Tao,et al.Shortterm photovoltaic generation forecasting system based on fuzzy recognition[J].Transactions of China Electrotechnical Society,2011,26(7):83-89.

[14] 邰能灵,侯志俭.小波模糊神经网络在电力系统短期负荷预测中的应用[J].中国电机工程学报,2004,24(1):24-29.

Tai Nengling,Hou Zhijian.New short-term load forecasting principle with the wavelet transform fuzzy neural network for the power systems[J].Proceedings of the CSEE,2004,24(1):24-29.

[15] 彭锦,刘宝锭.不确定理论及其公理化体系[J].黄冈师范学院学报,2004,24(3):1-9.

Peng Jin,Liu Baoding.Uncertainty theory and its axiomatic foundations[J].Huanggang Nornal University,2004,24(3):1-9.

[16] 刘宝锭,彭锦.不确定理论教程[M].北京:清华大学出版社,2005.

[17] 林媛.太阳辐射强度模型的建立及验证[J].安徽建筑工业学院学报,2007,15(5):44-46.

Lin Yuan.The model of the solar radiation energy’s establishment and verification[J].Journal of Anhui Institute of Architecture & Industry(Natural Science),2007,15(5):44-46.

[18] 申彦波,赵宗慈,石广玉.地面太阳辐射的变化、影响因子及其可能的气候效应最新研究进展[J].地球科学进展,2008,23(9):915-923.

ShenYanbo,Zhao Zongci,Shi Guangyu.The progress in variation of surface solar radiation,factors and probable climatic effects[J].Advances in Earth Science,2008,23(9):915-923.

[19] 张植明,田景峰.基于双重随机样本的统计学习理论的理论基础[J].计算机工程,2008,44(17):33-36.

Zhang Zhiming,Tian Jingfeng.Theoretical foundations of statistical learning theory of birandom samples[J].Computer and Applications,2008,44(17):33-36.

[20] 廖志凌,阮新波.任意光强和温度下的硅太阳电池非线性工程简化数学模型[J].太阳能学报,2009,30(4):430-435.

Liao Zhiling,Ruan Xinbo.Non-linear engineering simplification model of silicon solar cells in arbitrary solar radiation and temperature[J].Acta Energiae Solaris Sinica,2009,30(4):430-435.