电网电压不平衡下三相光伏发电系统的谐波电流抑制

周念成 楼晓轩 王强钢 王佳佳

（重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044）

0 引言

随着环境污染加剧和能源日益短缺，各国大规模开发风能、太阳能等可再生能源，与之相适应的分布式发电（Distributed Generation，DG）得到了高度重视和大力发展[1]。其中，光伏发电（Photovoltaic，PV）具有安装方便、技术成熟等优势，在分布式发电中应用广泛[2-5]。电力电子变换装置的非线性和电网谐波及不平衡电压等异常运行条件，都将导致光伏发电对电网电能质量造成不利影响[6-8]。特别是电网不平衡电压将导致光伏发电输出功率和直流电压发生波动，并使其端电流出现显著谐波畸变。为此，GB/T 20046—2006和IEEE Std.929—2000等标准均对光伏发电输出电流的总谐波畸变率和各次谐波含有率进行限制，以控制光伏发电对电网的谐波污染。因此，需要深入研究光伏发电在电压不平衡下的运行特性及其谐波电流的抑制方法。

针对电网电压不平衡下变流器的运行约束，文献[9,10]以直流侧恒定为控制目标，建立变流器正、负序电流的调节方案，但均未考虑变流器注入电流对电网电能质量的影响。为确保变流器运行满足并网电能质量要求，文献[11,12]提出5种有功和无功功率控制策略，使变流器接入点的功率波动和电流谐波达到不同的电能质量要求，据此文献[13]提出变流器有功和无功波动幅值连续可调的控制方案。针对光伏并网发电系统，已有文献对光伏发电的谐波电流抑制进行研究[6,7,14-16]。文献[14,7]分别提出减小单相和三相光伏发电谐波电流的控制方法，但未分析电压不平衡下光伏发电谐波电流的产生机理及其抑制措施。文献[6]研究了电压畸变不平衡下光伏发电并网电流指令计算和比例多重复数积分电流控制策略，但仅以有功恒定和单位功率因数运行为目标计算指令电流。实际上当电压不平衡下光伏发电功率波动完全消除时，将使光伏发电输出电流谐波严重越限[11]。为此，文献[15,16]利用α、β电流调节系数，提出电压不平衡下光伏发电的电流谐波和功率波动连续可调的控制策略，但仅对光伏发电的电流总谐波畸变率进行限制，因光伏发电并网标准中还对其输出电流的各次谐波含有率进行限制[17]，若仅考虑总谐波畸变率进行电流控制，将可能导致某次谐波出现越限，仍不能满足电网电能质量要求。

本文首先分析电网电压不平衡下光伏发电的功率控制和电流谐波产生机理，推导光伏发电的奇次谐波电流有效值的解析式，对电压不平衡下光伏发电的电流总谐波畸变率和各次谐波随电流调节系数变化规律进行分析，考虑各次谐波电流和功率波动限制，建立电压不平衡下光伏发电既满足总谐波畸变率、同时又能满足单次谐波限制的电流调节系数算法及控制策略。最后在PSCAD/EMTDC仿真平台中验证本文方法的可行性。

1 电网电压不平衡下的光伏发电功率控制

光伏并网发电系统及其功率控制结构如图1所示。光伏阵列采用受控电流源模型[18]，其输出功率随光照强度和温度波动变化。为了确保光伏阵列工作于最大功率运行点，图 1a中采集直流侧电压、电流udc和idc，通过最大功率点跟踪（Maximum Power Point Tracking，MPPT）模块计算最大功率点直流电压，作为直流电压指令udcr，进而得到功率指令Pr和Qr。同时在网侧采集电流、电压信息，结合功率指令计算指令电流iabcr，再由电流跟踪控制环节实现光伏并网发电系统的功率控制。

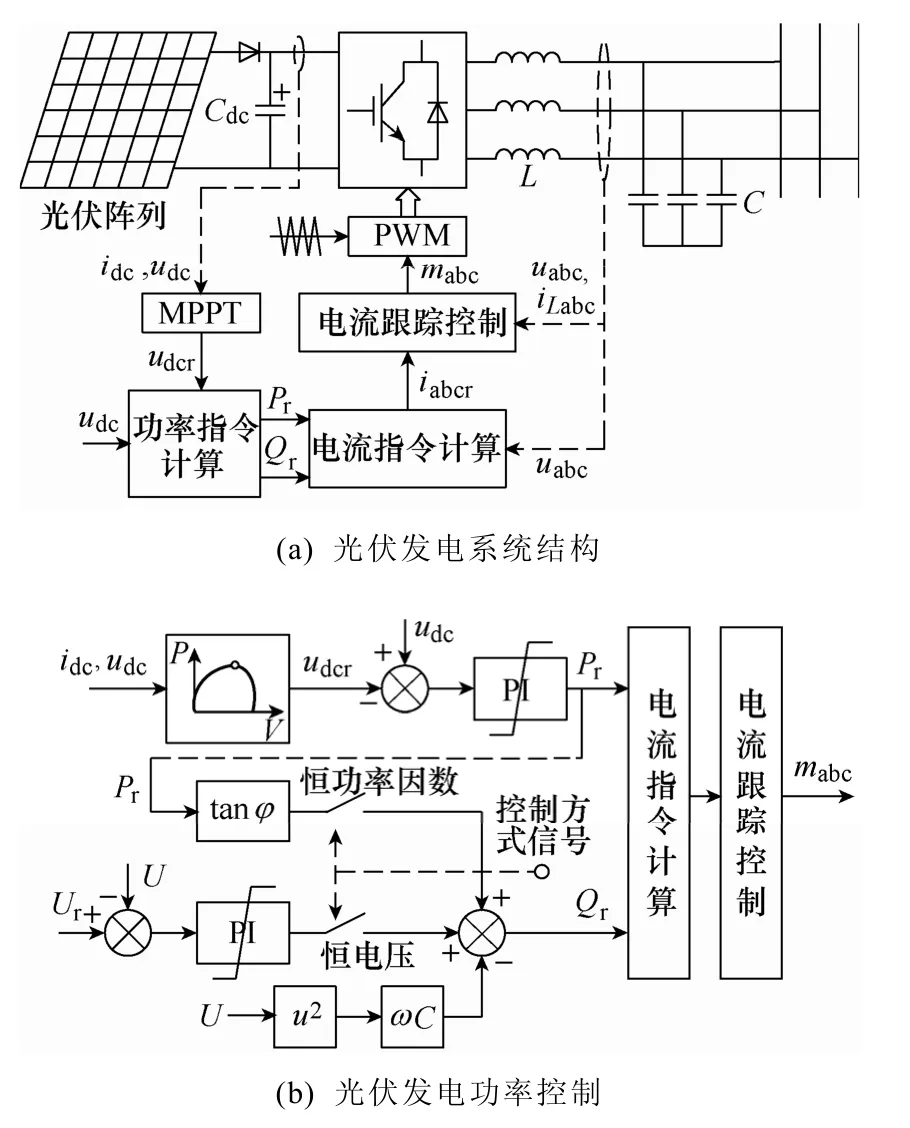
图1 光伏并网发电系统Fig.1 Diagram of grid-connected photovoltaic system

图1b中采用电导增量法[3,18]得到光伏阵列最大功率点参考电压udcr，与直流电压udc比较后经比例积分器生成有功指令Pr。而无功则有恒功率因数和恒电压两种控制方式，功率因数为cosφ时根据Pr计算无功指令，恒电压时则由光伏逆变器端电压有效值U与指令值Ur的偏差经比例积分器生成。由于电流跟踪采用电感电流反馈，图1b减去滤波电容无功后得到逆变器的无功指令Qr。目前，光伏发电最大功率跟踪已有较多文献研究[18-20]，下面重点讨论电网电压不平衡下光伏发电的电流指令计算及其谐波抑制。

配电网一般采用中性点不接地或经消弧线圈接地[11]，在三相三线制系统中不存在零序电流。电网电压不平衡时，光伏发电端电压含正、负和零序分量，电流仅含正、负序分量，采用空间矢量表示为

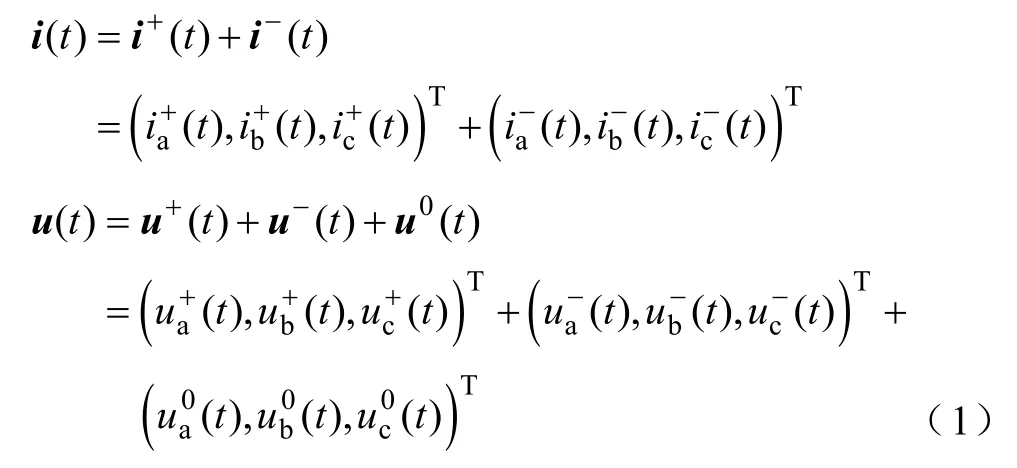
式中，u+(t)、u−(t)和i+(t)、i−(t)分别为光伏发电端电压和电流空间矢量的正序和负序分量，u0(t)为电压零序分量。则光伏发电三相瞬时有功功率为电压和电流矢量的点乘，即

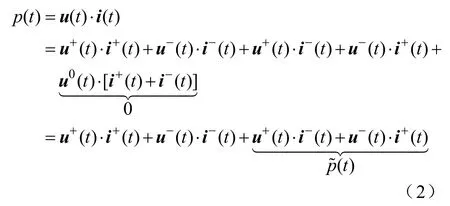
其瞬时无功功率为u(t)和i(t)矢量叉乘模值[11]，为便于计算构造与u(t)正交的电压矢量u⊥(t)，即

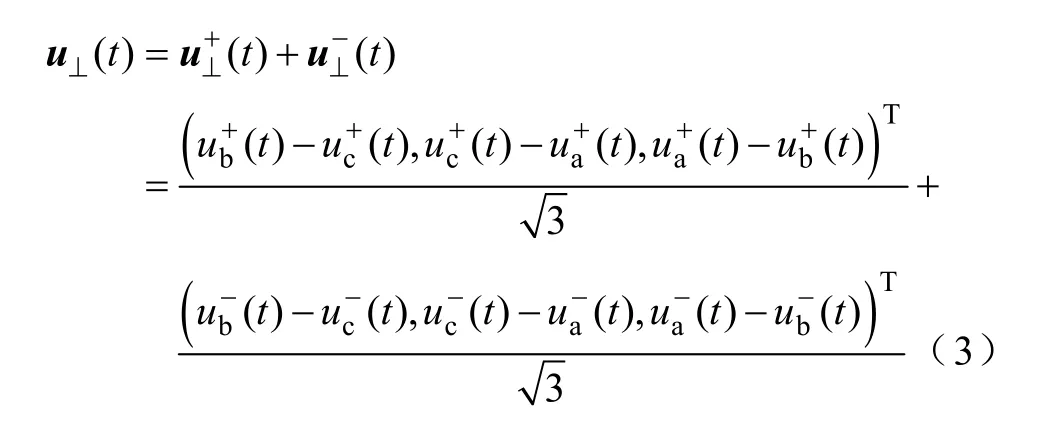
式中，电压矢量u⊥(t)的零序分量(t)=0，仅由正序和负序分量组成，则其三相瞬时无功功率为

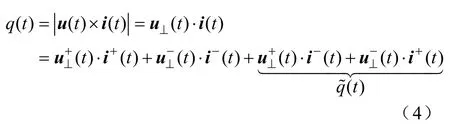
电网电压不平衡时，光伏发电端电压和电流正、负序分量的反向交叉，将使其瞬时有功和无功出现倍频波动(t)和(t)。根据式（3）推得u⊥(t)与u(t)矢量模值相等，即，为使电网电压不平衡时光伏发电有功和无功维持Pr和Qr恒定，由式（2）、式（4）可得其输出电流为

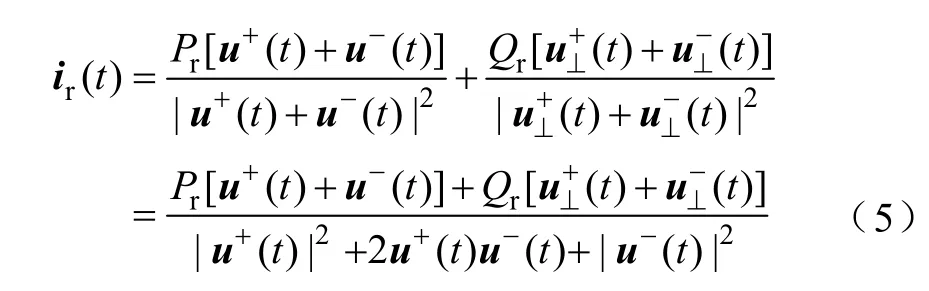
若采用式（5）计算光伏发电的电流指令，其输出功率可以完全跟踪功率指令Pr和Qr，进而消除输出功率波动。其代价是光伏逆变器输出电流将存在大量谐波[15]，因此需引入调节系数α、β以实现对逆变器电流谐波和功率波动的灵活控制。加入调节系数后的电流指令为

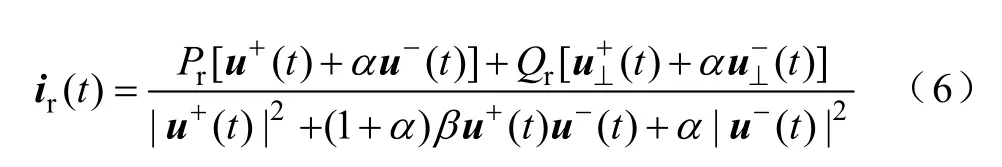
式中，α∈[−1,1]，β∈[0,1]，调节α、β系数可在一定范围内小幅增加光伏发电输出有功和无功功率波动幅值，同时确保逆变器电流谐波满足运行要求。

2 电网电压不平衡下光伏发电谐波电流特性分析计算

2.1 光伏发电电流谐波总畸变率及功率波动分析

根据光伏发电并网技术要求[17]，并网运行其平均功率因数必须大于0.9（超前或滞后）。因此，设注入电网的无功指令恒为零即Qr=0，光伏发电端电压负序与正序分量有效值之比为n=U−/U+。由式（6）可得光伏发电三相电流时域计算公式，其中a相为

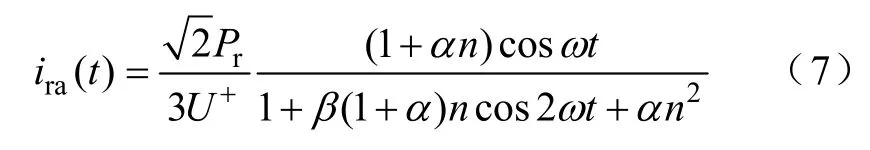
利用式（7）可分别推得电网电压不平衡时，光伏发电的基波和全波电流有效值I1和I，从而得到其电流总谐波畸变率为[15]

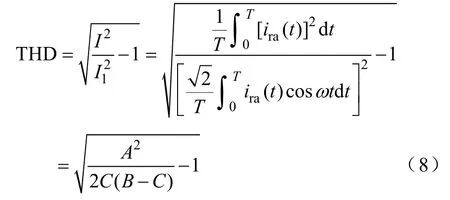
式中，A=β(1+α)n，B=1+αn2，。联立式（2）、式（4）和式（7）可得光伏发电系统的有功无功功率波动幅值为

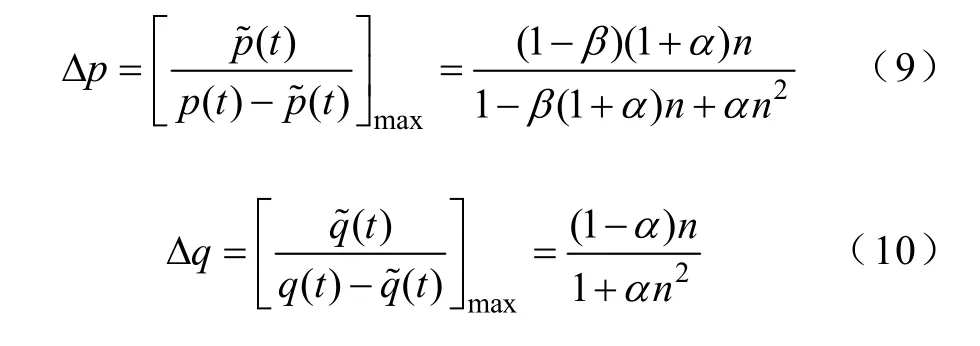
当电网电压负序不平衡度n=0.1，n=0.3，n=0.5三种情况时，根据式（8）～式（10）可计算光伏发电的电流总谐波畸变率和有功、无功功率波动幅值随α和β系数的变化特性，如图2所示。图中A1、A2和A3为系数(α,β)=(1,1)时三种情况下的谐波和功率波动，可见为了抑制光伏发电的有功和无功波动，其注入电网电流的总谐波畸变率将增大。由图 2可知，通过减小α和增大β能够降低有功波动，而抑制无功波动则通过增大α来调节，此外同时减小α和β能够降低逆变器输出电流谐波畸变率。因此电网电压不平衡时，需合理选择电流调节系数来保证光伏逆变器的输出电流满足谐波约束。

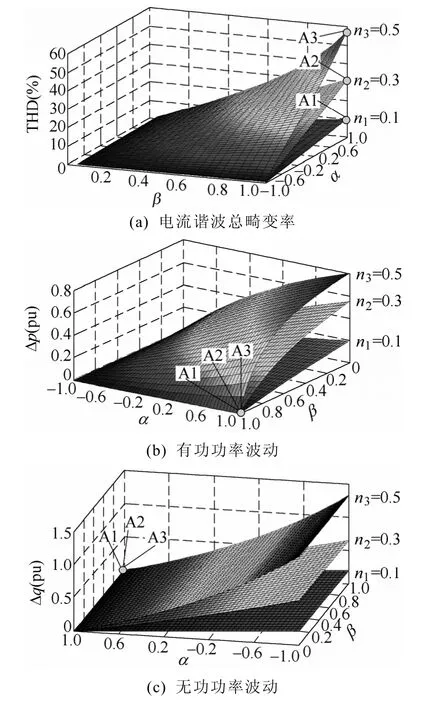
图2 电流谐波总畸变率和功率波动Fig.2 Three-dimensional mesh of current total harmonic distortion and power fluctuation magnitudes

2.2 光伏发电奇次电流谐波解析计算及分析

光伏发电并网标准中除了要求注入电网电流总谐波畸变率小于 5%外，还对其各次谐波电流进行限制。采用文献[15]中的方法只考虑电流总谐波畸变率来选择光伏发电电流调节系数时，可能使其某次电流谐波超出限值，仍不能满足光伏发电并网运行标准。电压不平衡下光伏发电的第k次电流谐波有效值Ik为

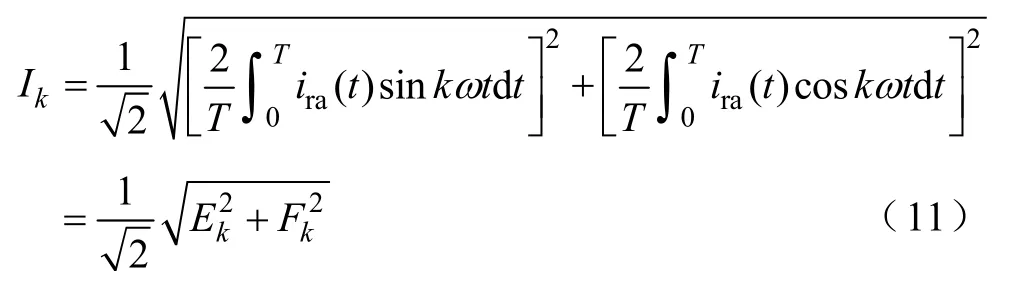
其中，光伏发电的偶次谐波电流含有率非常小，可忽略不计，下面主要针对其奇次谐波电流进行分析。将式（7）代入式（11），得电压不平衡时光伏发电端电流3次谐波的E3和F3分别为

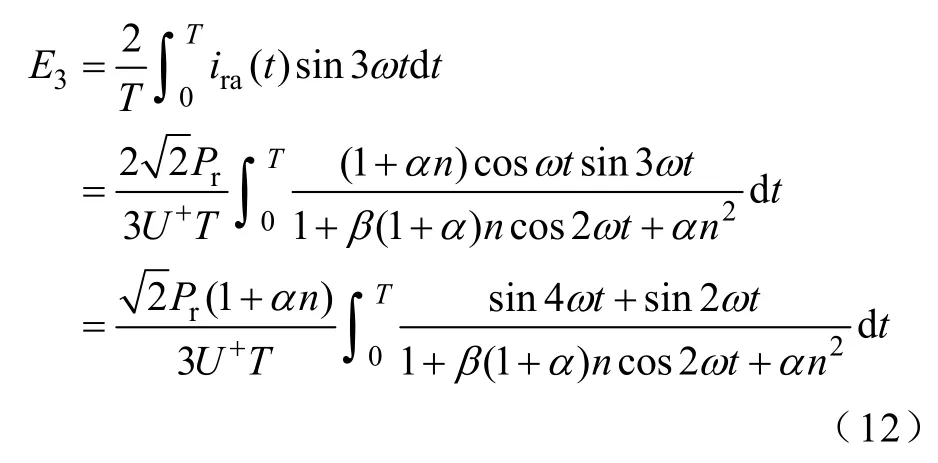
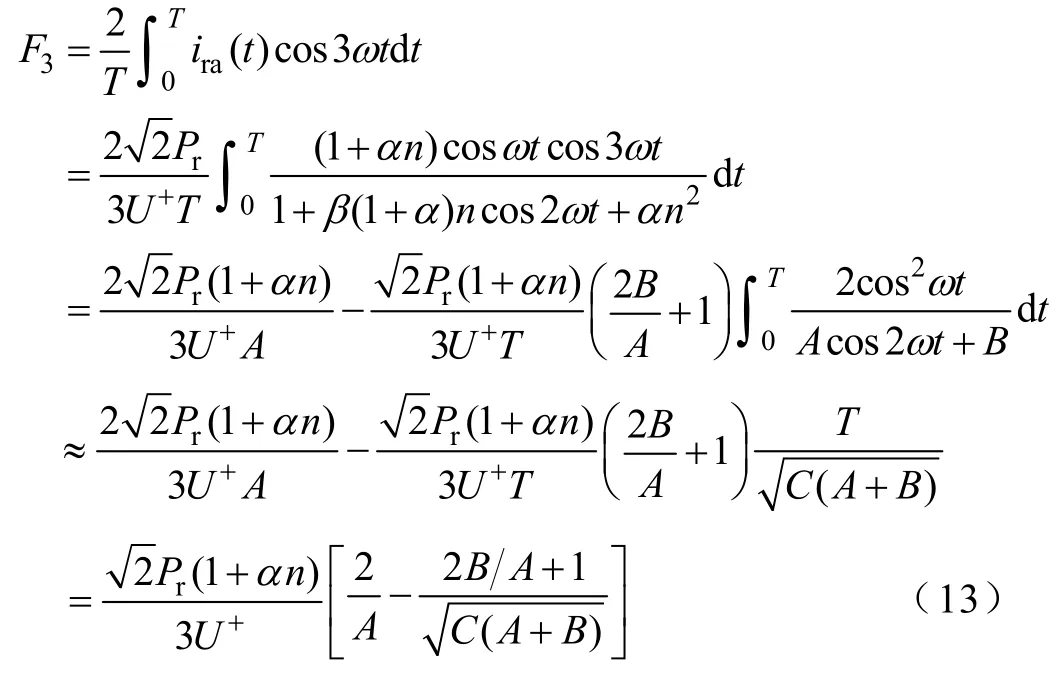
其中，积分项为奇函数使得E3=0，而采用数值方法可得式（13）中 2cos2ωt/(Acos2ωt+B)在周期T内的积分近似为T/[C(A+B)]1/2。则光伏发电输出电流的3次谐波有效值为

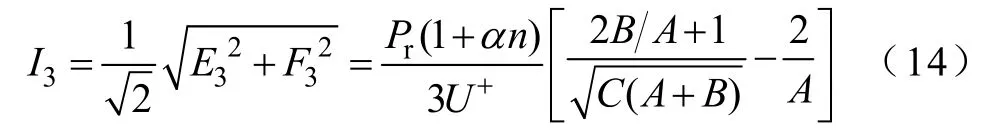
同理，可推导出电网电压不平衡下光伏发电输出电流的5次和7次谐波有效值为

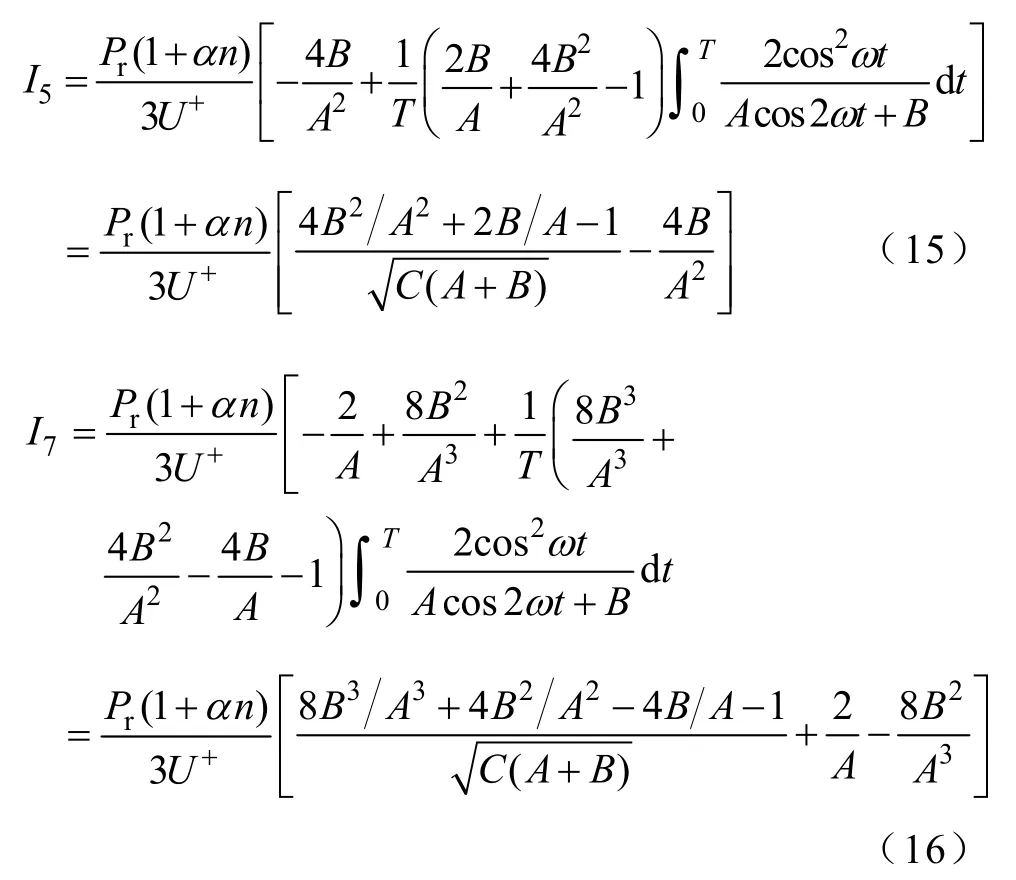
图3a所示为光伏发电输出电流的3～9次谐波有效值随α和β的变化特性，其中，Pr=1.0(pu)、U+=1.0(pu)，电压负序不平衡度n=0.3。与图2电流总谐波畸变率的变化趋势类似，随着α和β的增加，其3～9次谐波电流有效值逐渐增大，在(α,β)=(1,1)时光伏发电各次谐波电流含有率均达到最大。图3b给出了3次和5次谐波电流的仿真和计算结果，采用本文推导的计算式得到的结果与仿真基本吻合。电压不平衡时光伏发电的谐波电流有效值随谐波次数增加依次减小，并且9次及以上的奇次谐波电流含量很小，可忽略不计。

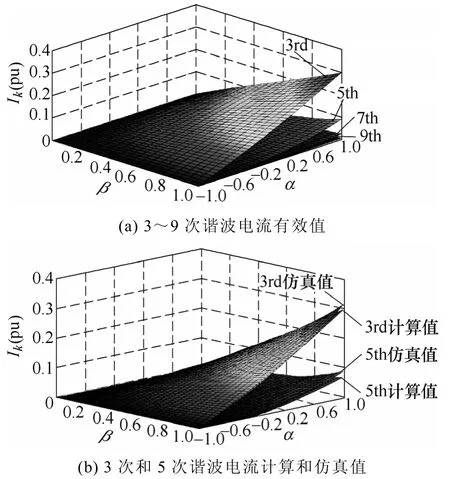
图3 奇次谐波电流有效值Fig.3 Three-dimensional mesh of odd harmonics current

对于额定电压380V、基准容量10MV·A的光伏发电系统，标准中规定其3～9次奇次电流谐波的允许值分别为0.004 1(pu)、0.004 1(pu)、0.002 9(pu)和0.001 4(pu)[17]。图4所示为光伏发电端电压负序不平衡度n=0.3时，其输出电流3～9次谐波、总谐波畸变率分别等于规定限值时的等高线。各等高线左下方区域为对应谐波限值所确定的α和β系数可行域，可见5次、7次和9次电流谐波的参数可选范围大于总谐波畸变率的范围，而3次电流谐波限值的可行域最小。仅考虑电流总谐波畸变率来选择α和β系数时，将使光伏发电3次谐波电流超过允许范围。

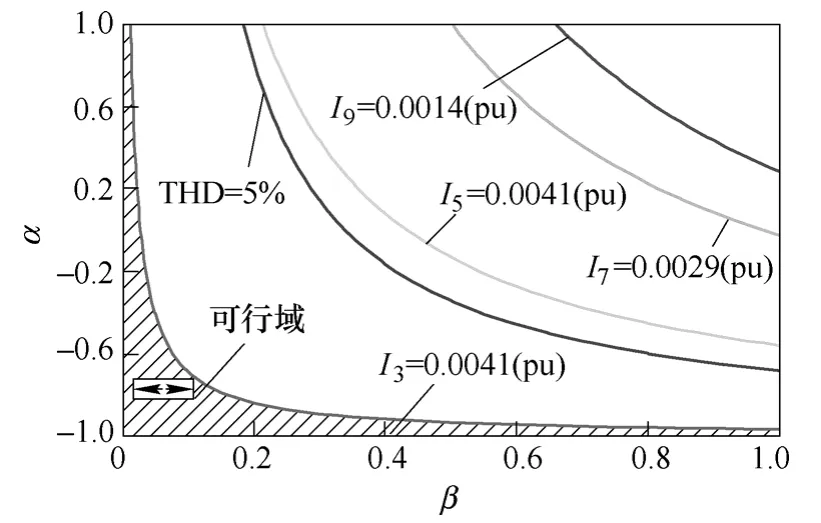
图4 奇次电流谐波和总谐波畸变率限值等高线Fig.4 The contour lines of odd harmonics current and current total harmonic distortion

根据光伏发电并网标准要求，电网电压不平衡时其电流总谐波畸变率、各次电流谐波均需小于给定的允许值。图4中光伏发电3次电流谐波限值的可行域即为综合上述电流谐波约束的α和β的可选范围。通过分析不同电压不平衡条件下，光伏发电各次电流谐波和总谐波畸变率的特性发现，在选择α和β系数时仅需对光伏发电的3次电流谐波进行限制，即可满足其余各次电流谐波和总谐波畸变率的限值要求。

3 电网电压不平衡下光伏发电谐波电流抑制策略

利用式（6）进行电网电压不平衡下光伏发电功率控制，当α和β取为不同整数时可得其功率波动和电流谐波特性见表1。由此可见，α和β系数的离散变化可使光伏发电的电能质量处于边界情况[11,12]。为了使电压不平衡下光伏发电的功率波动和电流谐波处于折中的运行点，需对α和β系数进行连续调节。

表1 不同调节系数下功率波动和3次谐波电流特性Tab.1 Power fluctuation and 3rd harmonic current characteristics under different adjustment coefficients

通过选择合适的α和β系数，可使光伏发电功率波动和电流谐波满足预定的要求，其中后者为电压不平衡下光伏发电必须满足的约束。因此，根据3次电流谐波限值I3r分别与无功波动限值ΔQr、有功波动限值ΔPr的组合，得到以下两种电流调节系数的确定方法。

（1）方式1：满足无功波动和3次谐波限值

电压不平衡下若光伏发电无功功率波动限值给定，利用式（10）可得α系数计算式如下

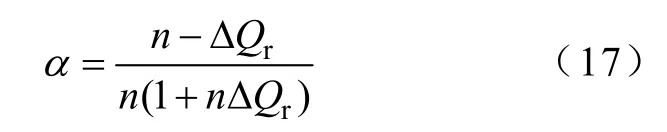
根据负序不平衡度n和无功波动限值ΔQr即可确定α系数，再由式（14）得光伏发电3次谐波电流为I3r时的求解方程为

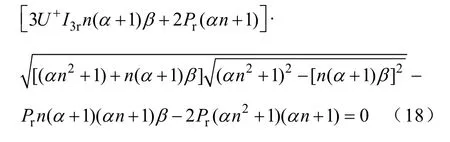
将式（17）代入式（18）得到关于β的一元方程，采用牛顿法解得同时满足无功波动和3次电流谐波限值的β系数，并选择β∈[0,1]内的实数解。

（2）方式2：满足有功波动和3次谐波限值

光伏发电有功功率波动限值给定时，可由式（9）得到α与β系数关系为

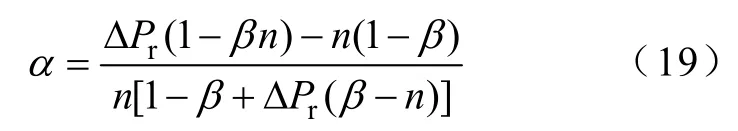
同理，将上式代入式（18）由牛顿法仍可求得满足有功波动和3次电流谐波限值的β系数，再将其反代入式（19）可得对应的α系数。

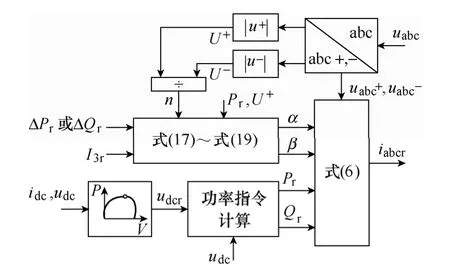
图5 计及谐波电流抑制的α和β系数在线调整Fig.5 Online adjustment ofα andβ coefficients for harmonic currents suppression

4 仿真分析

在PSCAD/EMTDC中建立图1所示的光伏发电模型，交直流额定电压为220V和1 000V，额定容量 2.5kV·A，L=12mH，C=0.7μF，Cdc=1 800μF。当光伏发电端电压发生负序不平衡度n=0.3的跌落时，不同α和β系数下其功率波动和3次、5次电流谐波的计算和仿真值见表 2。比较两组计算结果可知，上述推导的光伏发电功率波动和电流谐波解析式的计算值与仿真基本吻合。

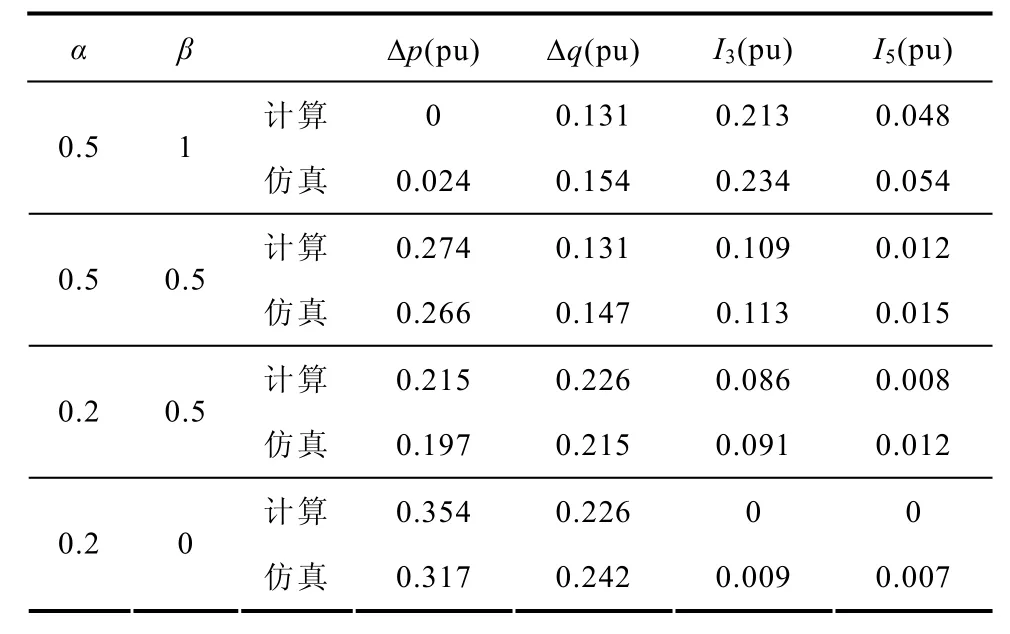
表2 不同调节系数下计算和仿真结果对比Tab.2 Comparison between calculation and simulation results under different adjustment coefficients

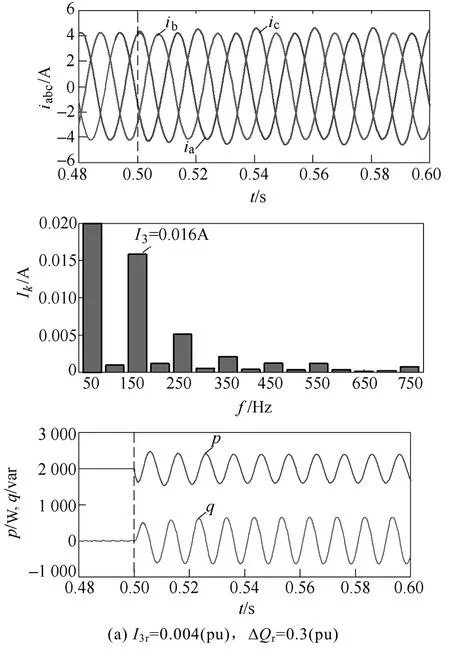
图6所示为采用控制方式1时光伏发电的电流瞬时值、各次电流谐波、有功和无功功率。在t=0.5s时其端电压发生n=0.3的跌落，图中给出了无功波动限值ΔQr=0.3(pu)不变，而 3次谐波限值为I3r=0.004(pu)和I3r=0.1(pu)的两种情况，两者调节系数(α,β)分别为(0.012,0.031)和(0.009,0.657)。

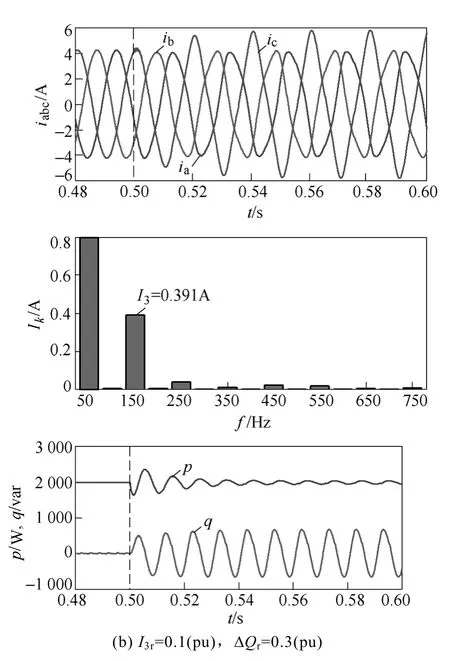
图6 采用控制方式1时的光伏发电运行特性Fig.6 Operation characteristics of photovoltaic generation using control mode 1

图6a和图6b的无功功率波动大小相同，均为0.288(pu)，与预定的无功波动基本一致。根据图6中各次电流谐波分布，电压不平衡下其电流谐波以奇次为主，不同调节系数下3次电流谐波均在各次电流谐波中占最大比例。图6a和图6b中3次电流谐波仿真值分别为0.004(pu)和 0.103(pu)，可见该控制方式可保证光伏发电的电流谐波运行于限定值。

图7所示为采用控制方式2时光伏发电在不平衡度n=0.2的端电压条件下的运行特性，其中有功限值固定为ΔPr=0.1(pu)，而 3次谐波限值为I3r=0.004(pu)和I3r=0.04(pu)。由于电压同步环节的作用，在光伏发电端电压跌落的瞬间，其瞬时功率会出现小幅的暂态分量[13]，其后图7a和图7b的调节系数(α,β)分别变化至(−0.458,0.124)和(−0.141,0.475)。随着光伏发电 3次电流谐波限值的提高，其无功波动的幅值逐渐减小。由图还可以看出，采用控制方式2能够同时确保光伏发电有功功率波动和电流谐波的自动调节。

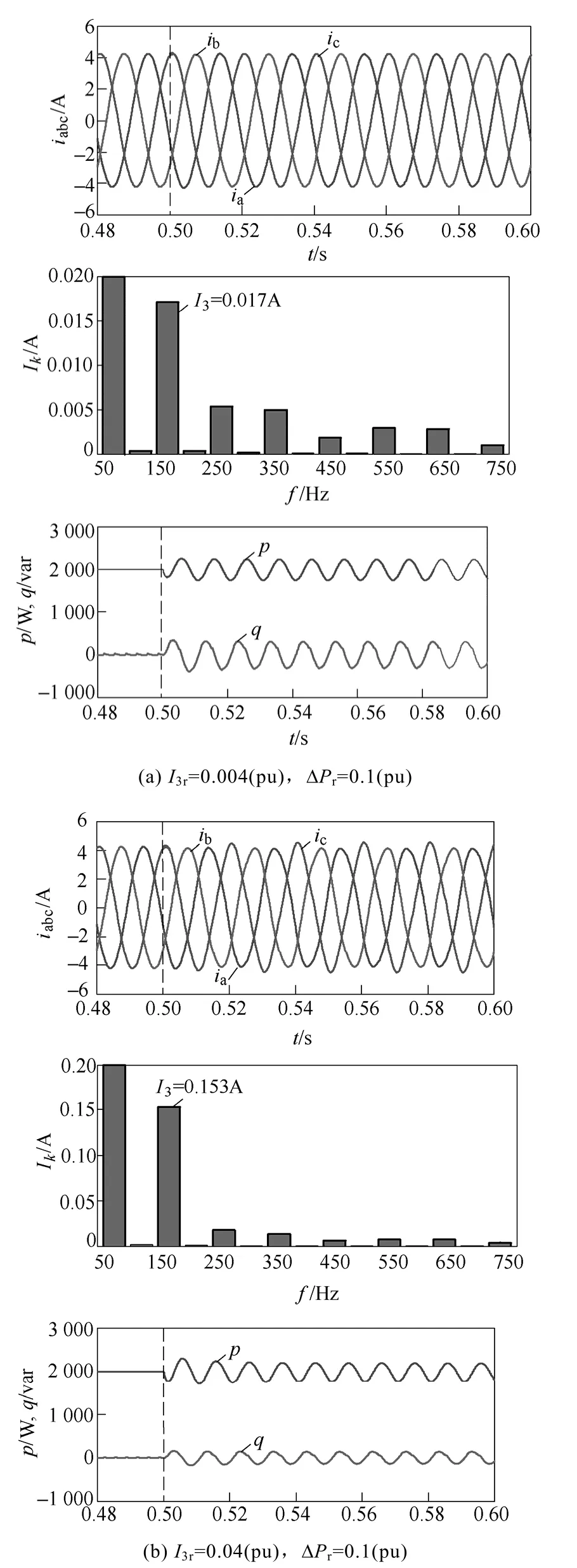
图7 采用控制方式2时的光伏发电运行特性Fig.7 Operation characteristics of photovoltaic generation using control mode 2

5 结论

本文提出了抑制电网电压不平衡下光伏发电输出电流谐波的控制策略。研究表明，通过对电流调节系数的连续调整，能够实现光伏发电功率波动和注入电网谐波的灵活控制，为此本文给出了电流调节系数的两种计算方法。通过对光伏发电系统仿真测试表明，推导的光伏发电功率波动和各次电流谐波解析式与仿真结果基本相同；提出的两种控制方式能够有效保障电网电压不平衡下光伏发电注入电网的功率波动和电流谐波，严格符合相关的光伏发电并网运行规定。

[1] Guerrero J,Blaabjerg F,Zhelev T,et al.Distributed generation:toward a new energy paradigm[J].IEEE Industrial Electronics Magazine,2010,4(1):52-64.

[2] Zhu Jizhong.Renewable Energy Applications in Power Systems[M].New York:Nova Science Publishers,2012.

[3] 周念成,邓浩,王强钢,等.光伏与微型燃气轮机混合微网能量管理研究[J].电工技术学报,2012,27(1):74-84.

Zhou Niancheng,Deng Hao,Wang Qianggang,et al.Energy management strategy of PV and micro-turbine hybrid micro-grid[J].Transactions of China Electrotechnical Society,2012,27(1):74-84.

[4] 张犁,孙凯,吴田进,等.基于光伏发电的直流微电网能量变换与管理[J].电工技术学报,2013,28(2):248-254.

Zhang Li,Sun Kai,Wu Tianjin,et al.Energy conversion and management for DC microgrid based on photovoltaic generation[J].Transactions of China Electrotechnical Society,2013,28(2):248-254.

[5] 周念成,闫立伟,王强钢.光伏发电在微电网中接入及动态特性研究[J].电力系统保护与控制,2010,38(14):119-127.

Zhou Niancheng,Yan Liwei,Wang Qianggang.Research on dynamic characteristic and integration of photovoltaic generation in microgrids[J].Power System Protection and Control,2010,38(14):119-127.

[6] 郭小强,邬伟扬,漆汉宏.电网电压畸变不平衡情况下三相光伏并网逆变器控制策略[J].中国电机工程学报,2013,33(3):22-28.

Guo Xiaoqiang,Wu Weiyang,Qi Hanhong.Control strategies of three-phase PV grid-connected inverter under distorted and unbalanced voltage conditions[J].Proceedings of the CSEE,2013,33(3):22-28.

[7] Castilla M,Miret J,Camacho A,et al.Reduction of current harmonic distortion in three-phase gridconnected photovoltaic inverters via resonant current control[J].IEEE Transactions on Industrial Electronics,2013,60(4):1464-1472.

[8] 王强钢,周念成,颜伟,等.采用背靠背变流器接入配电网改善低压微网电压质量的控制设计[J].电工技术学报,2013,28(4):171-181.

Wang Qianggang,Zhou Niancheng,Yan Wei,et al.Control design for voltage quality improvement of low voltage microgrid using back-to-back converter connected to distribution network[J].Transactions of China Electrotechnical Society,2013,28(4):171-181.

[9] Suh Y,Lipo T A.Control scheme in hybrid synchronous stationary frame for PWM AC-DC converter under generalized unbalanced operating conditions[J].IEEE Transactions on Industry Applications,2006,42(3):825-835.

[10] 姚骏,陈西寅,廖勇,等.电网电压不平衡时永磁直驱风电机组的控制策略[J].电力系统保护与控制,2011,39(14):99-106.

Yao Jun,Chen Xiyin,Liao Yong,et al.Control strategy of a direct-driven permanent-magnet synchronous generator wind turbine under unbalanced grid voltage conditions[J].Power System Protection and Control,2011,39(14):99-106.

[11] Rodriguez P,Timbus A V,Teodorescu R,et al.Flexible active power control of distributed power generation systems during grid faults[J].IEEE Transactions on Industrial Electronics,2007,54(5):2583-2592.

[12] Rodriguez P,Timbus A,Teodorescu R,et al.Reactive power control for improving wind turbine system behavior under grid faults[J].IEEE Transactions on Power Electronics,2009,24(7):1798-1801.

[13] Wang Fei,Duarte J L,Hendrix M A M.Pliant active and reactive power control for grid-interactive converters under unbalanced voltage dips[J].IEEE Transactions on Power Electronics,2011,26(5):1511-1521.

[14] Filho F,Tolbert L M,Cao Y,et al.Real-time selective harmonic minimization for multilevel inverters connected to solar panels using artificial neural network angle generation[J].IEEE Transactions on Industry Applications,2011,47(5):2117-2124.

[15] Castilla M,Miret J,Sosa J L,et al.Grid-fault control scheme for three-phase photovoltaic inverters with adjustable power quality characteristics[J].IEEE Transactions on Power Electronics,2010,25(12):2930-2940.

[16] Miret J,Castilla M,Camacho A,et al.Control scheme for photovoltaic three-phase inverters to minimize peak currents during unbalanced grid-voltage sags[J].IEEE Transactions on Power Electronics,2012,27(10):4262-4270.

[17] 国家电网公司.Q/GDW 617—2011光伏电站接入电网技术规定[S].北京:中国电力出版社,2011.

[18] 张明锐,林承鑫,徐瑞新.一种基于固态变压器的光伏发电并网技术[J].电力系统保护与控制,2012,40(19):133-138.

Zhang Mingrui,Lin Chengxin,Xu Ruixin,et al.Gridconnected photovoltaic power generation technology based on SST[J].Power System Protection and Control,2012,40(19):133-138.

[19] 郑必伟,蔡逢煌,王武.一种单级光伏并网系统MPPT算法的分析[J].电工技术学报,2011,26(7):90-96.

Zheng Biwei,Cai Fenghuang,Wang Wu.Analysis and research of MPPT algorithm for a single-stage PV grid-connected power generation system[J].Transactions of China Electrotechnical Society,2011,26(7):90-96.

[20] 刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6):91-94.

Liu Bangyin,Duan Shanxu,Liu Fei,et al.Photovoltaic array maximum power point tracking based on improved perturbation and observation method[J].Transactions of China Electrotechnical Society,2009,24(6):91-94.