串联结构中H 桥逆变器直流侧等效模型关系

杨维满 王兴贵

（兰州理工大学电气工程与信息工程学院 兰州 730050）

0 引言

自田纳西大学的F.Z.Peng 等人提出级联H 桥变流器电路拓扑以来，其应用范围已由初始的无功补偿系统逐步扩展到级联型有源滤波器、高压变频调速、链式D-STATCOM 等系统[1-5]。由于它自身输出电压波形正弦度好、谐波含量低，同一输出电压等级下可有效降低各单元直流侧电压大小，使得多个H 桥逆变单元之间保持串联连接的结构目前在光伏并网发电、微电网系统中均得到了灵活应用[6-9]。

逆变单元及所带等效负载整体作为系统中各支路直流侧典型负载，其动、静态特性对各自前端DC-DC 或AC-DC 变流器的控制设计、参数选择、动静态性能分析以及建模仿真都具有重要的影响作用。多单元串联结构中各单元之间相互关联、且存在运行与调制方面的约束条件，使得前端变流器设计与分析变得更加复杂。

目前，该类串联系统的研究主要集中于逆变单元控制方法上，如有功无功电流解耦控制、同步并网控制、均压控制以及功率平衡控制等方面[10-14]。对于系统建模方面的相关研究甚少，尚未发现串联结构中H 桥逆变器直流侧等效负载模型建立的有关研究报道。依据文献[15]研究SPWM-2H 桥逆变器直流侧等效模型的方法，本文特以三单元串联系统为例，研究得到不同直流侧输入电压、不同调制比例下串联H 桥各逆变单元的直流侧等效模型以及彼此之间的关系，并给出了对应的简化模型。这对前端变流器的独立设计与分析，以及串联系统不同单元之间的能量协调控制均具有重要意义。

1 H 桥逆变器串联电路结构及方程

三单元H 桥逆变器串联连接结构可用图1 所示电路进行等效。直流侧电压支撑电容划归为前端变流器部分，交流输出经LC 滤波后接入负载ZLoad；uC为输出滤波电容两端电压；Re表示逆变单元串联线路及电感损耗等效电阻；图中udci、idci、uoi（i=1，2，3）分别为各逆变单元直流侧输入电压、电流以及交流输出侧电压。

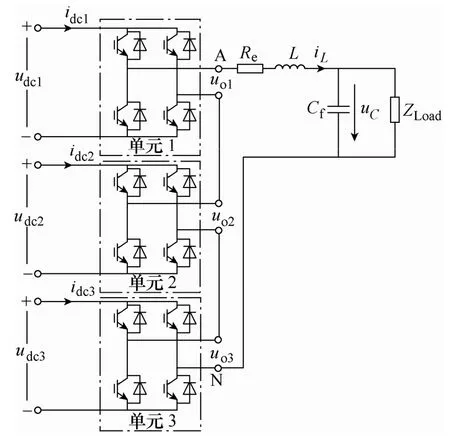
图1 三单元H-桥逆变器串联等效电路模型Fig.1 Equivalent circuit model of three H-Bridge inverters connected in series

串联结构中逆变单元通常采用载波相移-SPWM（Carrier Phase Shift-SPWM,CPS-SPWM）调制方法。各逆变单元输出电压uoi与直流侧电压udci之间的关系的双重傅里叶展开式为[16]

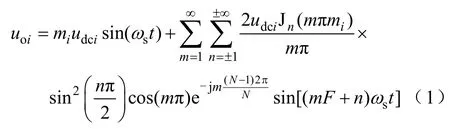
式中，mi为第i 个逆变单元的调制比；ωs为调制波角频率；F=(ωc/ωs)>>1为载波比，其中ωc为三角载波角频率；Jn(·)为n 阶Bessel 函数。

式（1）中右边第一项为输出电压基波分量，第二项为高次谐波项。考虑电压基波分量，结合图1得到串联系统输出电压uAN为

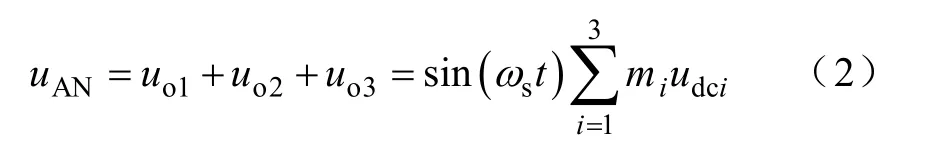
同时，各单元直流侧电流idci与滤波电感电流iL的关系满足

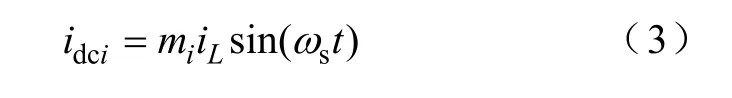
为减小单元之间的关联性，也可采用各单元正弦调制波频率、相位相等而幅值可调的改进型CPS-SPWM 方法。但无论采用何种方法，均需满足以下约束条件

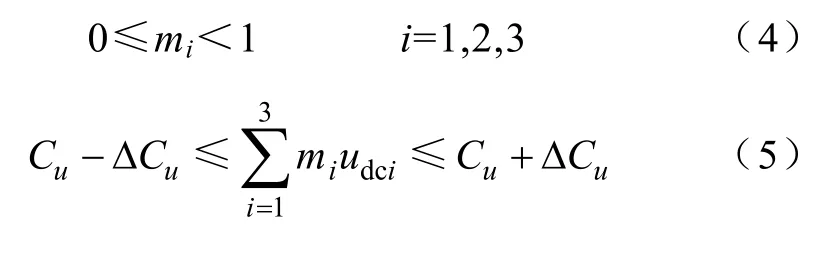
式中，Cu表示某一等级的电压恒定值；而ΔCu取值由电压允许波动范围决定。根据图1 列写串联系统中交流侧电压回路方程为

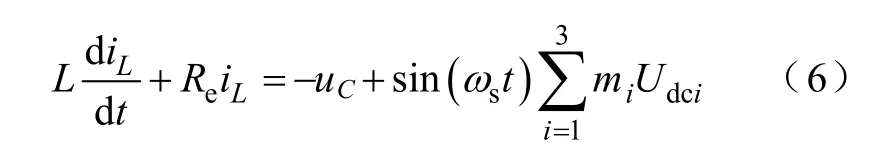
2 串联结构中H 桥逆变器等效模型分析

2.1 串联逆变器直流侧等效模型及关系

记Ui=miudci，可称其为受mi控制作用下的CPSSPWM 基波电压uoi的幅值。将其代入式（6）进一步得到

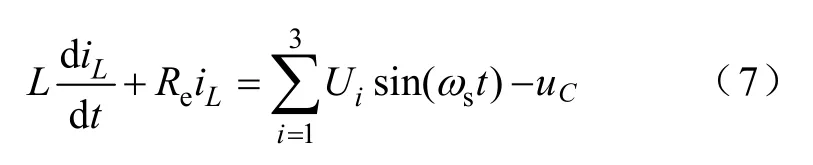
稳态运行时，设电容电压uC(t)与电感电流稳态解iLp的表达式分别为

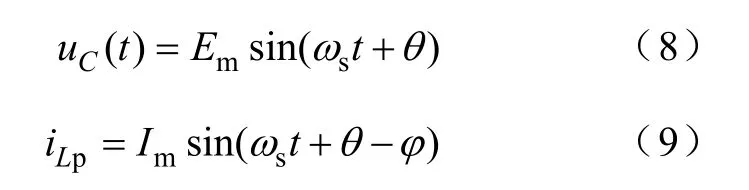
式中，Em为滤波电容两端电压幅值；θ为逆变单元输出电压与电容电压uC之间的相位差；φ为iL与uC之间的相位差。

将式（8）与式（9）同时代入式（7），则有

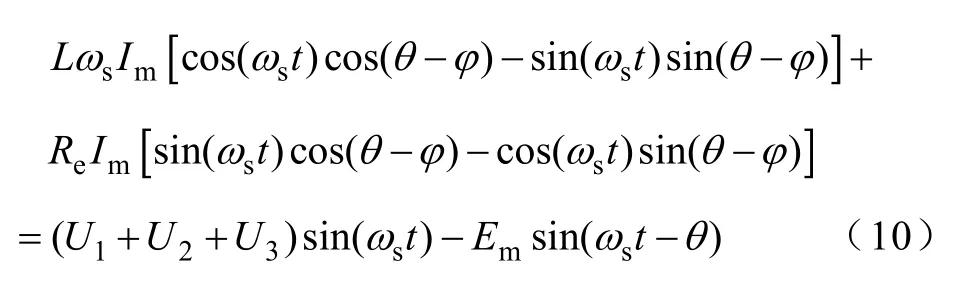
由于上式对任意时刻t 都成立，所以进一步有

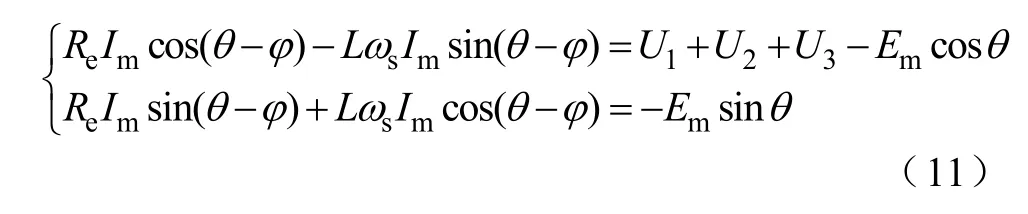
式（11）中两子式两端分别平方后相加得

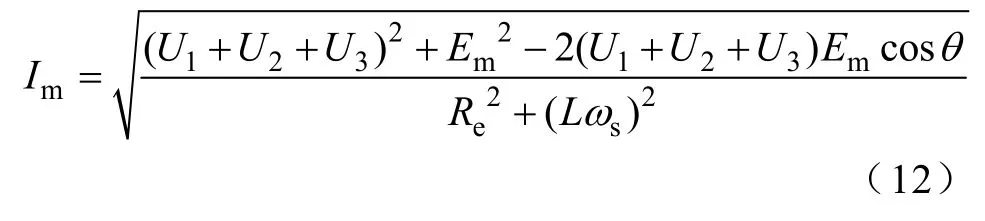
同时有

式中γ=arctan(Lωs/Re)。设式（6）全解为

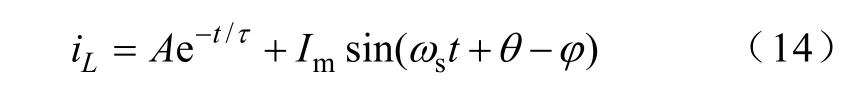
设初始条件iL(0)=0，将其代入式（14）即可得到A=-Imsin(θ-φ)，从而有

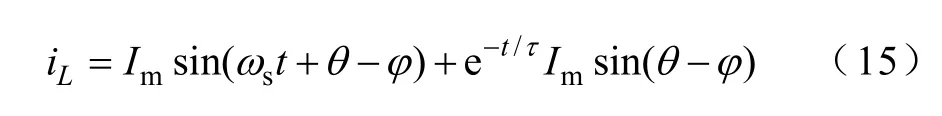
将式（15）、式（9）代入式（3）可得

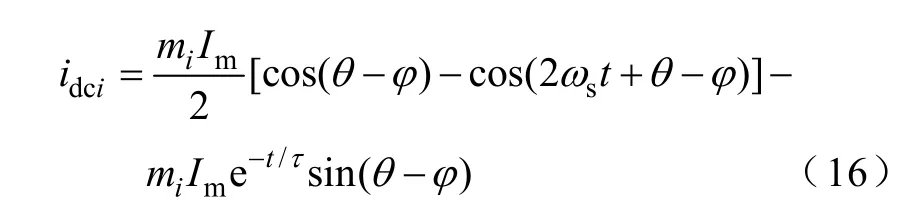
式（16）右边第一项为稳态分量，设为idcis。由于时间常数及电感参数较小，忽略第二项暂态分量则有

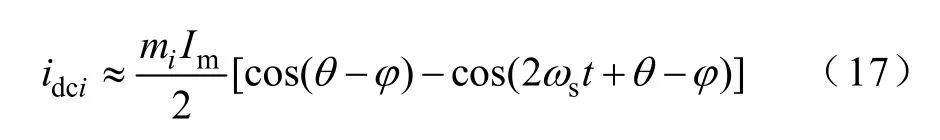
若令Em=ρ(U1+U2+U3)，ρ为反电动势幅度因数[16]，则根据式（12）有

将式（18）代入式（17），则有

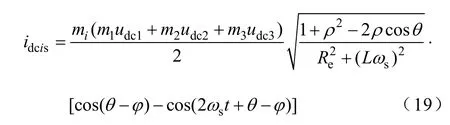
设pi=udci/ udc1，qi=mi/m1，文中将pi、qi（i=1，2，3）分别称为直流侧输入电压比例系数和调制比例系数。同时记

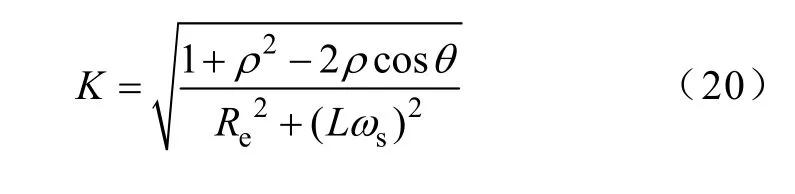
由式（19）、式（20）可得到串联结构中各单元在不同调制和输入情况下，直流侧稳态输入电导分别为

（1）情况1。当udc1≠udc2≠udc3、m1≠m2≠m3时

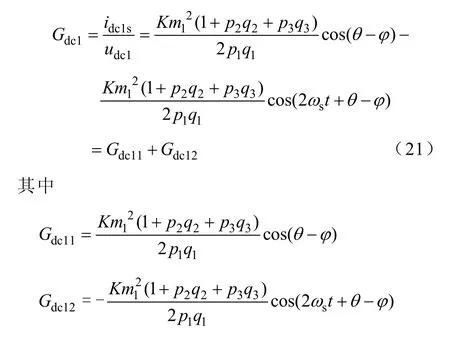
下文中所有Gdci1、Gdci2均按上述直流分量与交流分量方式进行拆分，同理可得

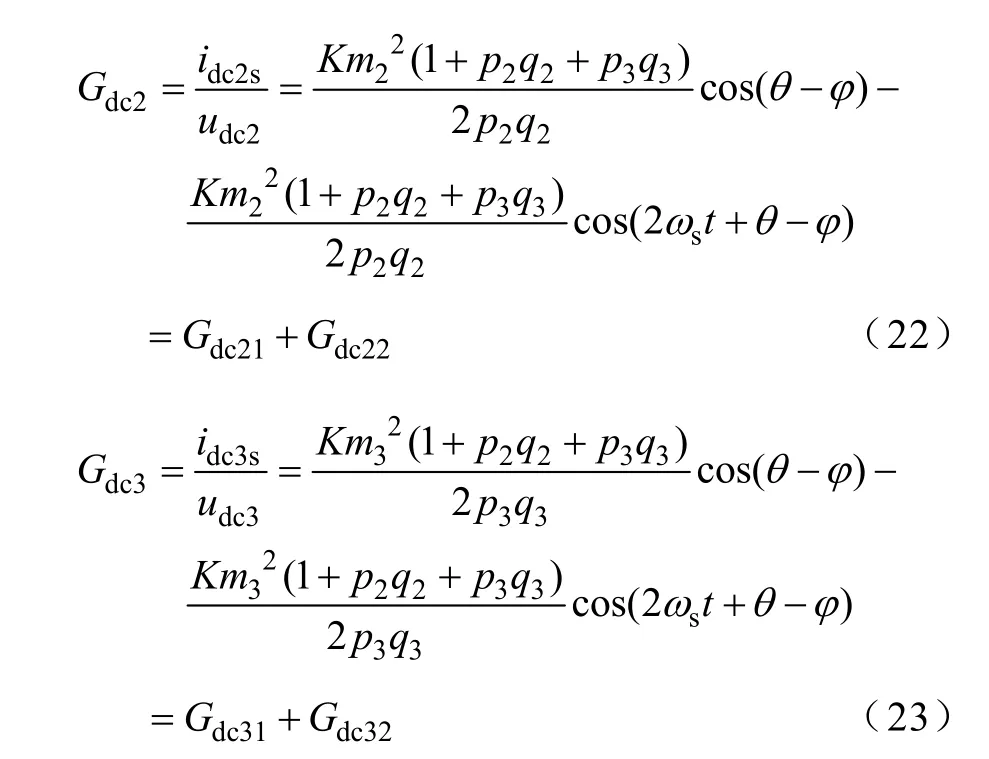
情况1 反映了各单元直流侧输入电压及调制比均不相等时各单元的稳态输入电导。由式（21）～式（23）可以看出，当电压Udci和调制比mi(i=1、2、3)均互不相等时，电导比Gdc1：Gdc2：Gdc3=(q1/p1)：(q2/p2)：(q3/p3)，即等于(m1/udc1):(m2/udc2):(m3/udc3)。下文中情况2、3、4 均为情况1 所示情况的一种特例。其运算方法相同，此处直接给出后三种情况下稳态输入电导的表达式。

（2）情况2。当udci=udc，mi=m（i=1,2,3）时

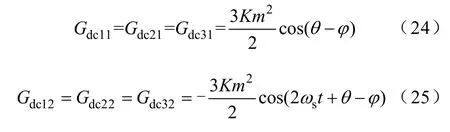
由式（24）、式（25）可看出:当串联逆变器各单元直流侧输入电压相等，且采用同一调制波时，各单元直流侧稳态输入电导Gdci相等。

（3）情况3。当mi=m，Udc1≠Udc2≠Udc3时

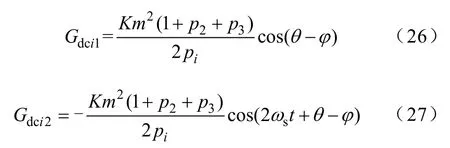
由式（26）和式（27）知，各单元采用同一调制波但直流侧输入电压不相等时，它们直流侧稳态输入电导Gdci彼此不相等。其比值Gdc1：Gdc2：Gdc3=(1/p1)：(1/p2)：(1/p3)，即为各单元直流侧输入电压倒数之比。

（4）情况4。当udci=udc，m1≠m2≠m3时

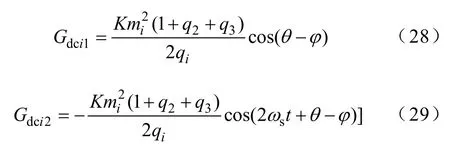
由式（28）、式（29）可以得知，当各单元直流侧输入电压相等，但采用频率、相位相等而幅值不等的不同调制波时，各直流侧稳态输入电导Gdci互不相等，其比值Gdc1：Gdc2：Gdc3=q1：q2：q3，即为各逆变单元的调制比例。

情况2～4为情况1 的几种特例，均存在p1=p2=p3=1 或q1=q2=q3=1 的特殊条件。故仅对式（21）～式（23）进行分析就可以得到不同情况下串联系统的一般特性:跟独立运行的单个H 桥逆变单元相同，各单元Gdci1、Gdci2或电流idcis中直流分量、交流分量之间相互关联。不同单元之间的比例关系由直流输入电压比例系数和调制比例系数共同决定。同时，从Gdci1可以看出|θ-φ|与90°的大于、小于或等于关系决定了交、直流两侧之间的功率流向。另外，Gdci2则反映了串联H 桥逆变单元两倍频脉动的固有特性。

2.2 逆变单元直流侧简化等效模型

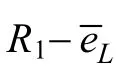
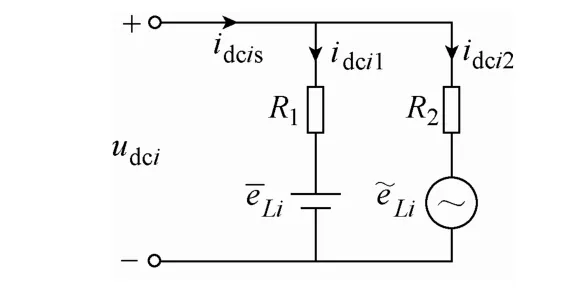
图2 逆变单元直流侧简化模型Fig.2 Simplified model on the DC side of the inverters

为使简化等效成立，idci1、idci2必须分别满足

则进一步得到

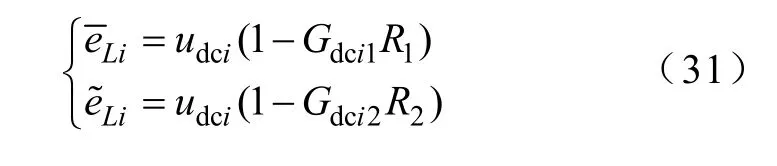
将式（21）～式（23）中Gdci1、Gdci2（i=1、2、3）分别代入式（31），则可得到情况1 下各单元所对应简化模型等效参数为

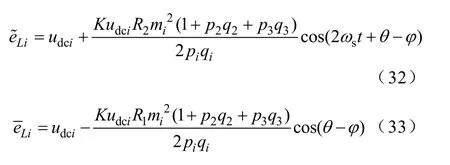
情况2、3、4 简化等效模型参数获取方法与情况1 的相同。分别将式（24）～式（29）依次代入式（31）即可，此处不再一一列写。

3 仿真与实验分析

3.1 仿真分析

本文基于 Matlab/Simulink 软件平台对所建直流侧等效模型的正确性进行仿真分析。具体参数:滤波电感、电容分别为L=3mH、Cf=60μF，调制波频率fs=50Hz，载波比F=40，阻感性负载中L=6mH、R=2Ω。同时，经计算得到θ、φ 分别为3°、42°。而直流侧输入电压udci和调制比mi依据四种不同情况分别进行取值，仿真结果分别如图3～图6 所示。由于不同情况下各逆变单元直流侧等效模型及简化等效原理相同，此处仅对单元1、2 在四种不用情况下的等效模型分别进行分析。

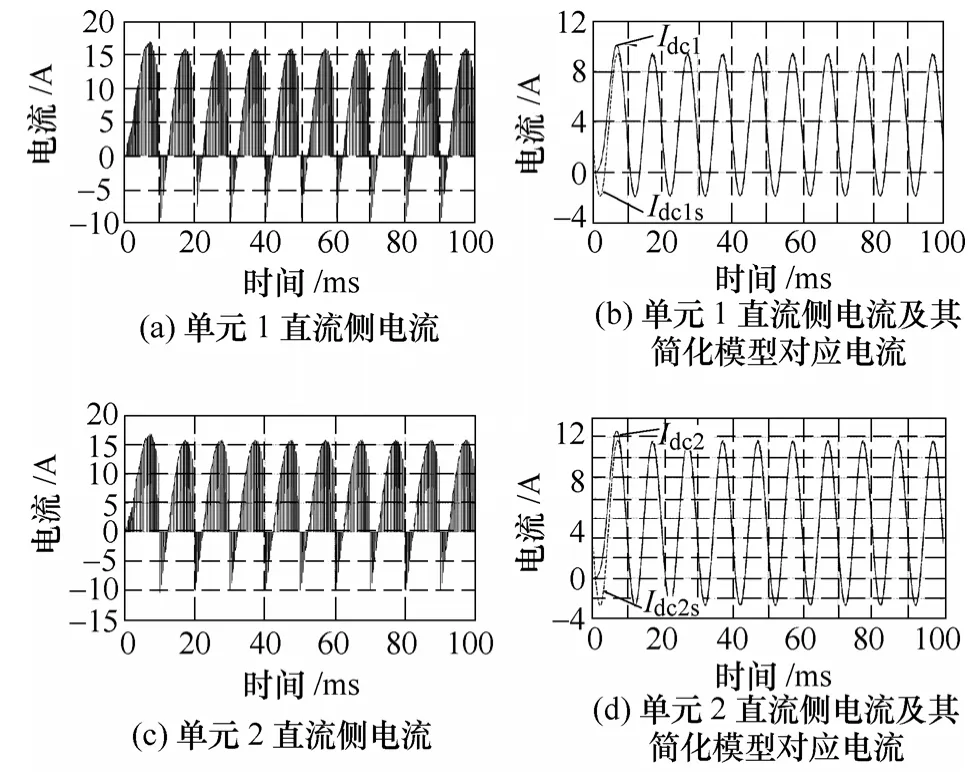
图3 情况1 时直流链电流及简化模型对应电流Fig.3 Current waveforms of DC and corresponding simplified model in case 1

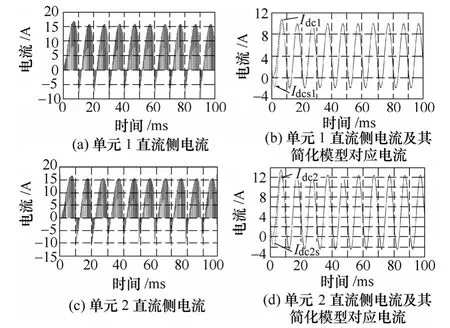
图4 情况2 时直流链电流及简化模型对应电流Fig.4 Current waveforms of DC and corresponding simplified model in case 2

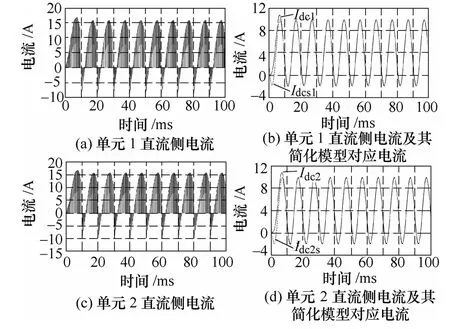
图5 情况3 时直流链电流及简化模型对应电流Fig.5 Current waveforms of DC and corresponding simplified model in case 3

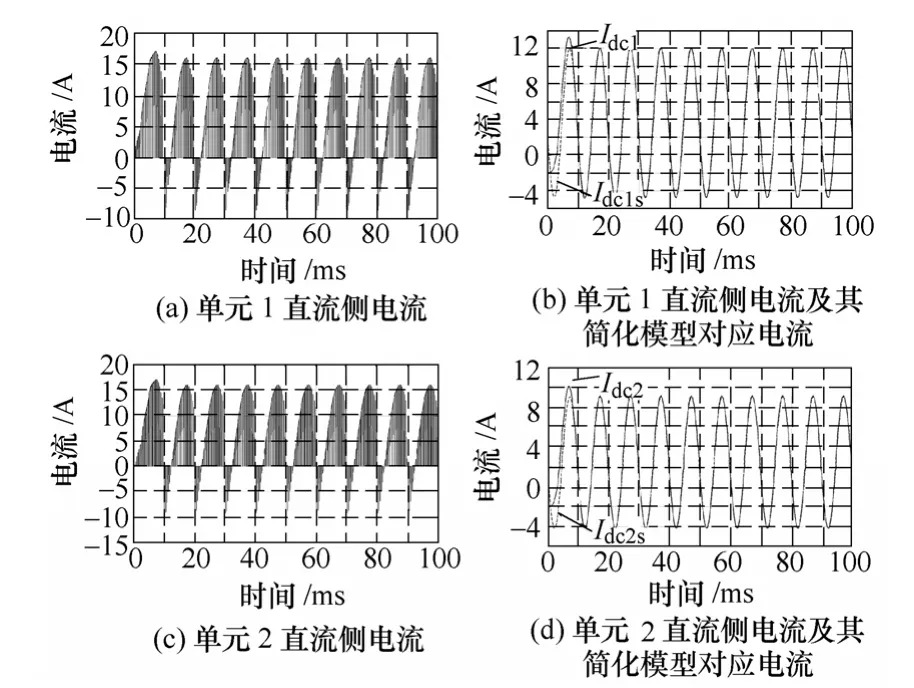
图6 情况4 时直流链电流及简化模型对应电流Fig.6 Current waveforms of DC and corresponding simplified model in case 4

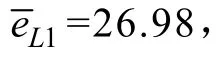
图3b、图3d 中，Idc1、Idc2及Idc1s、Idc2s分别表示单元1、2 低通滤波后的直流侧电流和简化模型对应直流电流。可以看出约经过半个脉动周期后电流Idcis波形完全覆盖了Idci(i=1,2)的波形，由此说明稳态运行后简化模型可完全作为逆变单元直流侧等效负载模型。

情况2、3、4 中调制比与直流侧电压取值分别如下。

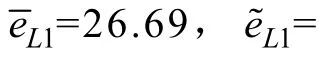
结合图3～图6 可以看出:在这四种情况下简化模型均可实现逆变单元直流侧负载模型的等效。同时，也可以反映出各单元直流电流特性相同。

3.2 实验分析

搭建了H 桥逆变单元串联实验系统，并基于此进行了不同输入电压和调制比的电能变换实验。主要实验参数为:未做特殊说明时调制波频率 fs=50Hz、载波比N=40；阻感性负载中R=6Ω、L=12mH。滤波电感、电容分别为2mH 和30μF。

直流输入电压和调制比分别取值为:①udc1=12V，udc2=20V，udc3=16V，m1=0.8，m2=0.88，m3=0.85；②udc1=udc2=udc3=16V，m1=m2=m3=0.85；③udc1=12V，udc2=20V，udc3=16V，m1=0.85，m2=0.85，m3=0.85；④udc1=udc2=udc3=16V，m1=0.95，m2=0.75，m3=0.85。图7 给出了不同输入作用下单元1、2 直流侧电流波形，与图3～图6 中对应仿真波形特性相同。

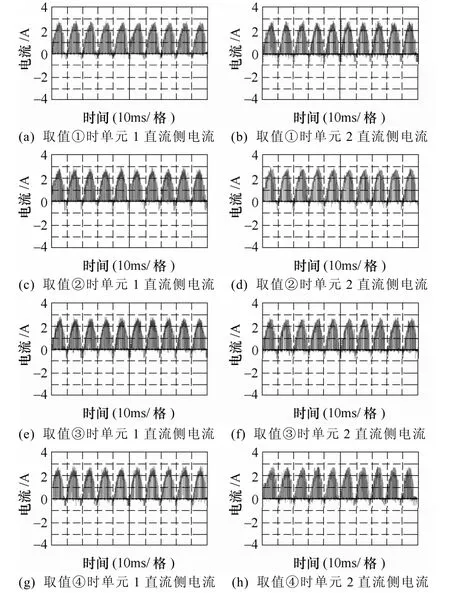
图7 不同取值下单元1、2 直流侧电流Fig.7 DC link current waveforms of the cell 1 and 2 in different cases

图8 给出了三个H 桥逆变单元串联后输出的多电平电压波形。对比图8a 和图8b 可以发现:当各单元直流侧输入电压和调制比相等时，串联环节输出了规则的七电平电压，即每个台阶内各脉冲幅值相等（均为16V）且自身对称。而当取值①时，该环节输出不规则的多电平电压。另外，还发现两种输入情况下多电平电压在一个工频周期内的电压脉冲数目相等，这一点是由两种取值情况下的相同载波比所决定。

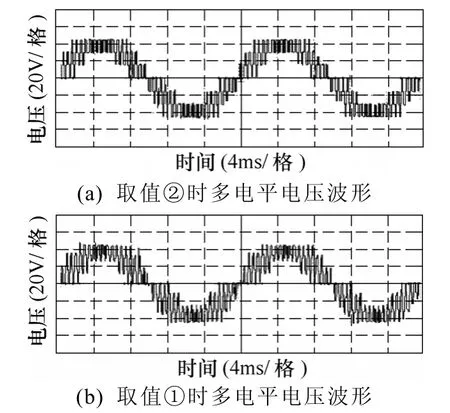
图8 不同取值时串联环节输出多电平电压波形Fig.8 Output voltage waveforms with multilevel waveform under different input values

图9 反映了系统各单元直流侧电压和调制比取值②时，交流侧部分负载投切前后单元1 直流侧电流的变化情况。对比图9a 与图9b 可以得知:部分负载切除后，即阻感性负载变化为R=12Ω、L=12mH时，单元1 直流侧电流脉冲幅值减小，而脉动特性与先前保持一致。这完全可由文中直流侧等效模型对应变量进行描述。

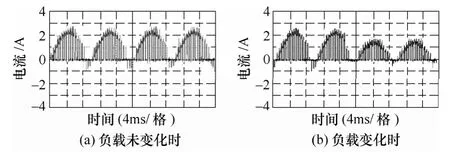
图9 部分负载投切前后单元1 直流侧电流Fig.9 DC link current waveforms of the cell 1with load change

图10 中两子图分别给出了fs=25Hz、N=40 和fs=50Hz、N=20 时单元1 直流侧电流波形。从图10a可以看出直流侧电流脉动周期为20ms，与图9a 相比其脉动周期扩大一倍。由此可进一步说明直流侧电流二倍频调制波频率脉动的固有特性，这一点在本文所给等效模型中已反映出。由图10b 可以看出一个工频周期内直流侧电流脉冲数目减少，为图9a所示的一半。这是由于此时载波比N=20，而图9所示情况中N=40 所致。

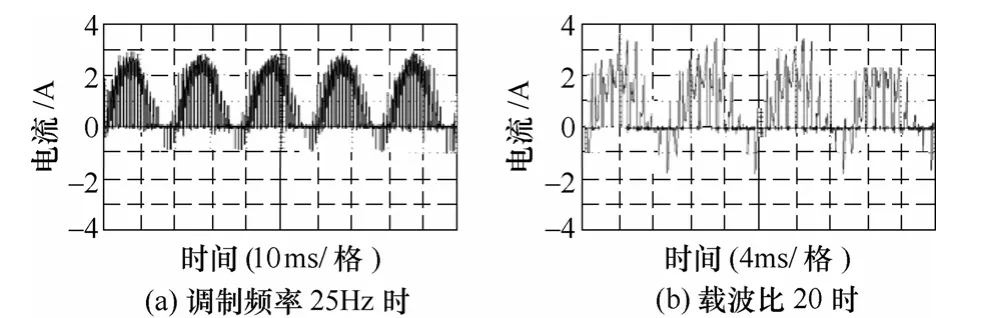
图10 调制比、载波比改变后单元1 直流侧电流Fig.10 DC link current waveforms of the cell 1 after the change of modulation index and carrier-ratio

图11 显示了调制比、直流侧电压取值②时，滤波电感电流及负载电压、电流波形。图11a 所示为流过滤波电感的电流，对比图7 发现它们满足式（3）所示关系。图11b 显示了阻感性负载电压与电流之间的超前关系，输出频率满足50Hz。在整个实验过程中还发现:在满足式（4）和式（5）所示约束条件下，改变输入电压比例系数pi和调制比例系数qi，电感电流及负载电压、电流未发生变化。

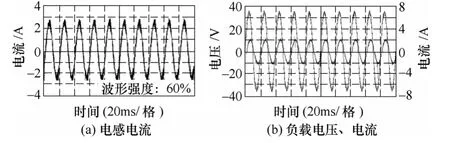
图11 滤波电感电流及负载电压、电流Fig.11 Filtering inductance currents and load voltage,load current waveforms

4 结论

（1）各逆变单元的直流侧等效负载之间满足特定比例关系，且由调制比例系数、直流侧输入电压比例系数共同决定。由此为前端变流器的独立分析、设计，以及串联系统各单元之间的功率协调控制与分析奠定了基础。

建模过程主要考虑了输出电压的基波分量，所得模型无法反映直流侧负载的高频开关特性，这是本文所建等效模型的一个不足之处。另外，死区时间会给串联环节输出电压引入低次谐波成分，并对直流侧等效模型产生一定影响。本课题组接下来将对它们进行重点研究。

[1]Peng F Z,Lai J S.A multilevel voltage-source inverterwith separate DC sources for static var generation[J].IEEE Transaction on Industry Applications,1997,32(5)：1130-1138.

[2]李建林,赵栋利,赵斌,等.载波相移SPWM 级联H 型变流器及其在有源电力滤波器中的应用[J].中国电机工程学报,2006,26(10)：109-113.Li Jianlin,Zhao Dongli,Zhao Bin,et al.Cascade H bridge converter with carrier phase shifted SPWM technique and its application in active power filter[J].Proceedings of the CSEE,2006,26(10)：109-113.

[3]孙运全,尹强,盛吉,等.载波带频率变化的PWM(VFCB-PWM)在级联有源电力滤波器中的应用[J].电力系统保护与控制,2010,38(10)：39-43.Sun Yunquan,Yin Qiang,Sheng Ji,et al.Variable frequency carrier bands PWM (VFCB-PWM) and its applications in shunt APF[J].Power System Protection and Control,2010,38(10)：39-43.

[4]宫力,康勇,陈晶晶,等.链式 STATCOM 直流电容电压分布式控制[J].电工技术学报,2011,26(10)：218-233.Gong Li,Kang Yong,Chen Jingjing,et al.DC capacitor voltage distributed control system for cascaded multilevel STATCOM[J].Transactions of China Electrotechnical Society,2011,26(10)：218-233.

[5]谢化安,王永源,万四维,等.东莞变电站链式STATCOM 控制保护的RTDS 试验研究[J].电力系统保护与控制,2013,41(4)：117-122.Xie Huaan,Wang Yongyuan,Wan Siwei,et al.Research on the control and protection system of Dongguan substation cascade static synchronous compensator based on RTDS[J].Power System Protection and Control,2013,41(4)：117-122.

[6]Villanueva E,Correa P,Rodríguez J.Control of a single-phase cascaded H-bridge multilevel inverter for grid-connected photovoltaic systems[J].IEEE Transaction on Industrial Electronics,2009,56 (11)：4399-4406.

[7]黄立培,马毅为,孙凯,等.高效级联式光伏并网逆变器的控制[J].高电压技术,2011,37(3)：680-686.Huang Lipei,Ma Yiwei,Sun Kai,et al.Control of high efficiency cascaded photovoltaic grid-connected inverter [J].High Voltage Engineering,2011,37(3)：680-686.

[8]杨维满,王兴贵.光伏微源特性对串联型微网电压稳定性的影响[J].电网技术,2013,37(9)：2446-2451.Yang Weiman,Wang Xinggui.Research on influence of micro-source characteristics on voltage stability of the series micro-grid[J].Power System Technology,2013,37(9)：2446-2451.

[9]陈元娣,夏敏学,朱忠尼.基于阶梯波与瞬时值反馈混合控制的光伏并网级联逆变器[J].电力系统自动化,2012,36(14)：172-176.Chen Yuandi,Xia Minxue,Zhu Zhongni.Photovoltaic grid-connected cascaded inverter based on stepped waveforms and instantaneous value feedback hybrid control[J].Automation of Electric of Power Systems,2012,36(14)：172-176.

[10]查晓明,张茂松,孙建军.链式D-STATCOM 建模及其状态反馈精确线性化解耦控制[J].中国电机工程学报,2010,30(28)：107-113.Zha Xiaoming,Zhang Maosong,Sun Jianjun.Modeling of cascade D-STATCOM with decoupled state variable feedback linearization control[J].Proceedings of the CSEE,2010,30(28)：107-113.

[11]杨晓峰,范文宝,王晓鹏.基于模块组合多电平变换器的 STATCOM 及其控制[J].电工技术学报,2011,26(8)：7-13.Yang Xiaofeng,Fan Wenbao,Wang Xiaopeng.Static synchronous compensator based on modular multilevel converter based STATCOM and its control[J].Transactions of China Electrotechnical Society,2011,26(8)：7-13.

[12]耿攀,吴卫民,叶银忠.基于重复控制的单相分时复合级联光伏逆变器控制[J].电工技术学报,2011,26 (3)：116-122.Geng Pan,Wu Weimin,Ye Yinzhong.Single-phase time-sharing cascaded photovoltaic inverter based on repetitive control[J].Transactions of China Electrotechnical Society,2011,26(3)：116-122.

[13]孙宜峰,阮新波.级联型多电平逆变器的功率均衡控制策略[J].中国电机工程学报,2006,26(4)：126-132.Sun Yifeng,Ruan Xinbo.Power balance control schemes for cascaded multilevel inverters[J].Proceedings of the CSEE,2006,26(4)：126-132.

[14]王志冰,于坤山,周孝信.H 桥级联多电平变流器的直流母线电压平衡控制策略[J].中国电机工程学报,2012,32(6)：56-63.Wang Zhibing,Yu Kunshan,Zhou Xiaoxin.Control strategy for DC bus voltage balance in cascaded H-bridge multilevel converters[J].Proceedings of the CSEE,2012,32(6)：56-63.

[15]许胜,赵剑锋,倪喜军,等.SPWM-2H 桥逆变器直流侧等效模型[J].电工技术学报,2009,24(8)：90-94.Xu Sheng,Zhao Jianfeng,Ni Xijun,et al.The DCside equivalent model of SPWM 2H-bridge inverter[J].Transactions of China Electrotechnical Society,2009,24(8)：90-94.

[16]张加胜,张磊.PWM 逆变器的直流侧等效模型研究[J].中国电机工程学报,2007,27(4)：103-107.Zhang Jiasheng,Zhang Lei.Research on the DC-side equivalent model of PWM inverters[J].Proceedings of the CSEE,2007,27(4)：103-107.