风电全功率变流器参数对可靠性的影响分析

杨珍贵 杜 雄 孙鹏菊 周雒维

（重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044）

0 引言

风电变流器在全功率风电结构中起到解耦及电能转换的作用，将机侧的变频输入转换为网侧的恒频输出[1]，是风能转换系统中的核心元件。然而风机的恶劣工作环境，通常使得风电变流器的可靠性相比其他工业领域里要低[2]。文献[2]中，通过对超过6 000台陆地风电机组历时11年的可靠性数据统计，得到风电机组中各子系统的失效率如图1所示。由图1可知，风电变流器失效率非常高，仅次于电气系统。为了降低运行及维护成本，亟需对风电变流器的可靠性进行分析，以提出相应的改善措施，确保低成本、长期可靠的运行环境。

图1 风电机组中各子系统的平均失效率分布Fig.1 Distribution of average failure rates over wind turbine subsystems

文献[3]指出，风电变流器失效中超过50%的故障是由于功率半导体器件造成，而器件的性能主要与工作温度、湿度及承受的电应力有关[4,5]，尤其是器件的结温及其幅值波动很大程度上决定了它们的失效速率[5]。由于风速变化的随机性，风机的输出功率及器件的损耗也跟着发生相应的变化，器件的工作温度也发生随机波动，以致严重影响了风电变流器的可靠运行。

鉴于器件工作温度对变流器可靠性的重要影响，目前，有诸多文献基于器件的工作温度对工业应用中变流器的可靠性进行了研究。文献[6,7]基于器件结温幅值大小评估了不同变流器拓扑结构的可靠性差异，缺乏考虑器件温度波动的影响；文献[8]给出了航空三相功率变流器在一种工作状态下的可靠性设计步骤，却没有分析负载变化造成器件工作温度波动对变流器可靠性的影响；文献[9]对小型风能转换系统中两种不同变流器拓扑工作在额定状态下的可靠性进行比较，缺乏分析风速变化造成器件温度波动对变流器可靠性的影响；文献[10]分析影响风电变流器可靠性的影响因素时，考虑了风速变化的影响，而变流器系统参数的影响却没有深入研究。根据现有的文献报道，业界针对变流器可靠性的研究主要是基于设计初始阶段，考虑变流器在一种工作状态下的可靠性优劣，而对于因风速随机变化使得风电变流器频繁工作在多种状态下的可靠性研究，目前还比较少。

本文以永磁同步风力发电机（Permanent Magnet Synchronous Generator，PMSG）连接着“背靠背”的二电平全功率变流器为例，如图2所示，结合实测的风速及气温数据，分析论证了变流器参数——功率因数、开关频率及散热热阻的变化，导致器件工作温度变化对变流器可靠性的影响。

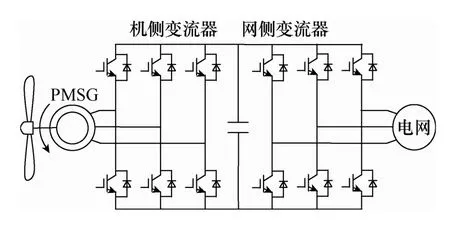
图2 PMSG风电机组拓扑结构Fig.2 Topology of PMSG wind turbine

本文首先根据温度对器件失效的机理，综合考虑铝键合线失效和焊料层疲劳两种失效模式，给出了功率半导体器件的可靠性预测模型。利用风机输出功率与变流器中器件损耗及结温的关系，结合器件的温度计算，得出变流器可靠性的预测流程图。然后以实际风速数据为例，分析论证了变流器系统参数对变流器可靠性的影响，并初步讨论提高变流器可靠性的措施。

1 全功率风电变流器的可靠性评估

1.1 可靠性评估模型

由于构成功率半导体器件材料之间的热膨胀系数差异，当器件的工作温度发生变化时，材料形成不同程度上的压缩或拉伸而产生剪应力，逐渐累积之后导致器件发生热疲劳失效[4,5]。在功率循环波动下，功率绝缘栅双极晶体管（Insulated Gate Bipolar Transistor，IGBT）器件中最常见的失效类型主要有两种：铝键合线失效与焊料层疲劳失效。文献[5]给出了IGBT铝键合线功率循环失效周期数Nf与结温变化大小ΔTj及平均结温Tm关系，如图3所示。从图中可以看出，随着Tm或ΔTj的增大，失效周期数越短，且ΔTj对器件寿命的影响比Tm更加显著。

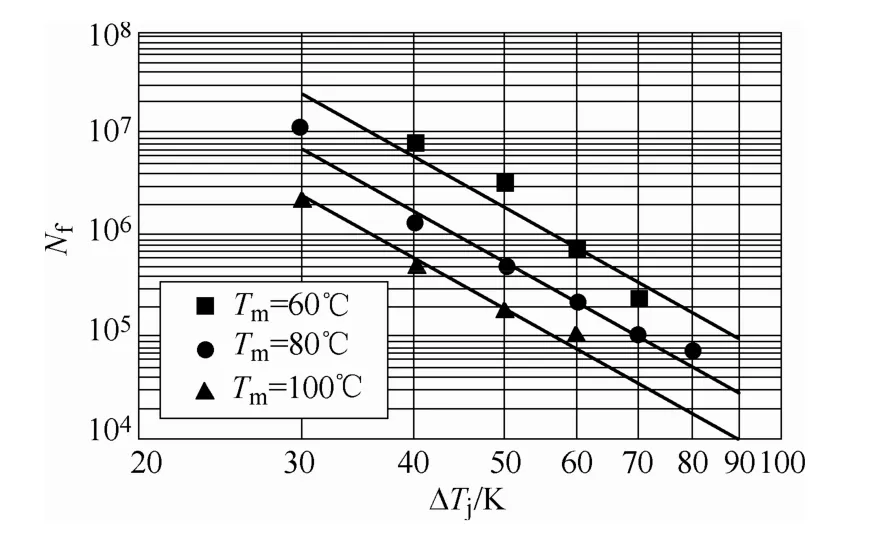
图3 功率循环失效周期数Nf与Tm及ΔTj的关系Fig.3 Number of power cycles to failureNfas function ofΔTjandTm

功率循环失效周期数与Tm及ΔTj的关系可表示为[5]

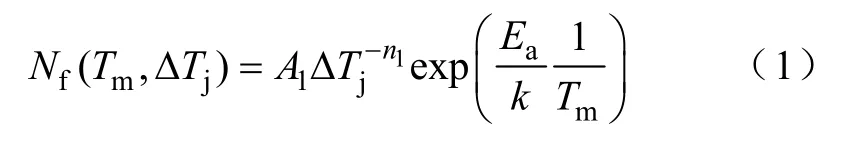
式中，Nf(Tm,ΔTj)为Tm及ΔTj下的功率循环失效周期数；参数A1、n1是与功率模块相关的常数，可以由试验数据拟合得到，本文分别取值为302 500和 5.039；Ea为激活能量常数，取值9.89×10−20J；k为玻耳兹曼常量[11]。

发生焊料层疲劳失效的寿命模型可以用壳温变化大小ΔTc表示为[12]

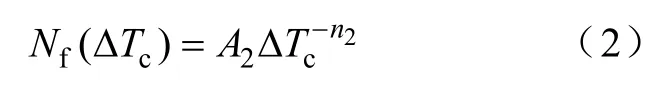
式中，Nf(ΔTc)为在壳温变化ΔTc下的功率循环失效周期数；参数A2、n2同样由试验数据拟合得到[13]，本文分别取值为1.3×1023和10.1。

为了预测功率器件的平均失效时间（Mean Time To Failure，MTTF），通常采用线性疲劳损伤积累模型，由此，IGBT铝键合线的MTTF计算式为[14]

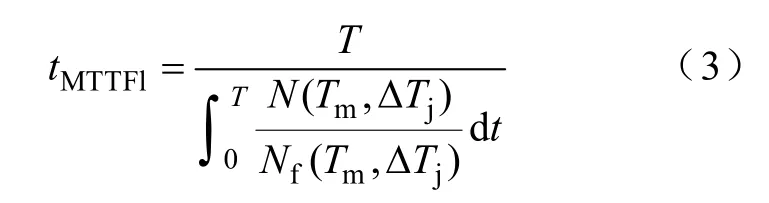
式中，T为负载功率循环下的单位循环时间；N（Tm,ΔTj）为每个时间T内，在ΔTj及Tm下对应的功率波动循环个数。同理，可以获得 IGBT焊料层的平均失效时间tMTTFs。

器件失效率的计算模型是在不同失效机理下产生的各自失效率叠加起来的，而失效率又可表示为MTTF的倒数[15,16]，因此，单个 IGBT的失效率可以表示为

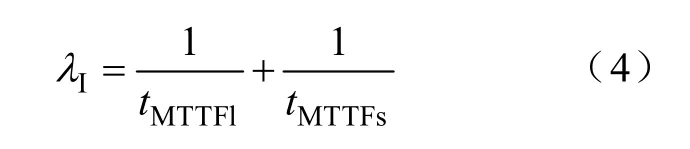
根据文献[17]，由多个电子元件组成系统的失效率λtotal可以表示为各个电子元件失效率的叠加，因此，风电变流器的失效率计算式为

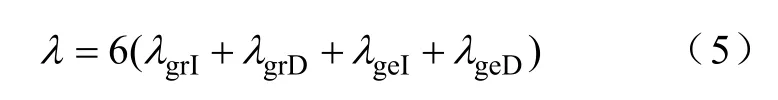
式中，λgrI与λgrD分别表示网侧IGBT与二极管的失效率；λgeI与λgeD分别表示机侧IGBT与二极管的失效率。

1.2 结温与壳温计算

三相变流器的简化热模型如图4所示[18]，图中，PI与PD分别表示IGBT与二极管在一个正弦输出周期内的平均损耗；Rjc与Rch分别表示 IGBT结到壳与壳到散热器之间的热阻；Rjcd与Rchd分别表示二极管结到壳与壳到散热器之间的热阻；Rha表示散热器到环境之间的热阻，由散热条件决定；Tamb表示环境温度。由图 4可知，IGBT结温与壳温的计算式为

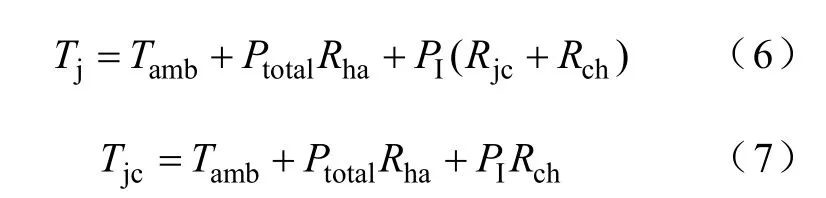
式中，Ptotal为三相变流器的总损耗，即 6个 IGBT模块损耗的和。同理，可以计算二极管的结温Tjd与壳温Tjcd。损耗PI、PD及Ptotal的具体计算可以参考文献[14]。

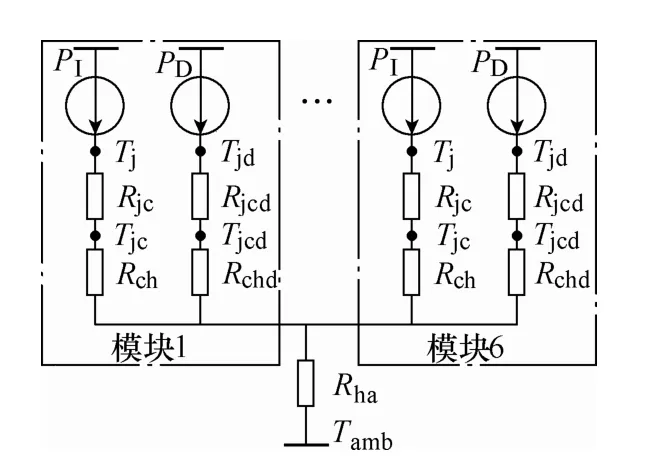
图4 三相变流器的简化热模型Fig.4 Simplified thermal model of three phase converter

每个温度循环中，结温变化的同时也包含了壳温的变化，结温幅值变化大小ΔTj与平均结温Tm[17]计算式为

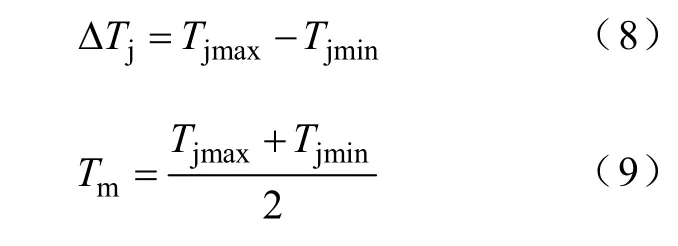
式中，Tjmax与Tjmin分别为一个温度循环中结温的最大值与最小值。壳温变化ΔTc的计算式为

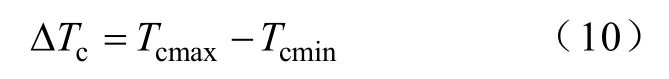
1.3 可靠性评估方法

风机的输出功率通常可通过风电场测量的实时数据来反映[22]或风速来估算[10]，由于获得单台风机的实时功率输出较为困难，于是，本文利用风速数据，根据风机的输出功率曲线特性来估算风机的功率输出，并以此作为评估风电变流器可靠性的基础[10]。基于上述分析，风电全功率变流器可靠性的评估步骤如图5所示，首先结合风速数据计算风机的输出功率，接着利用变流器的系统参数进行损耗计算，然后考虑气温数据结合变流器热模型得到器件的结温及壳温，之后计算每个温度循环的ΔTj、Tm及ΔTc以评估变流器的可靠性。

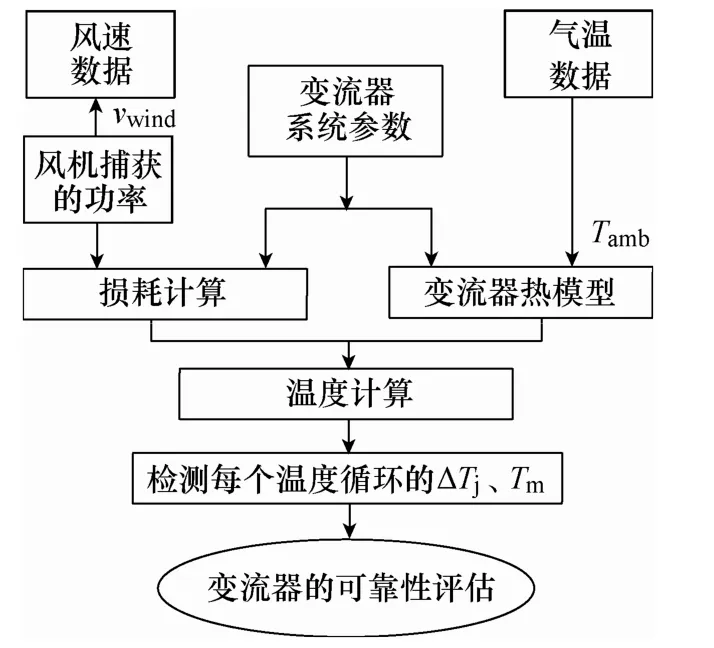
图5 风电系统中变流器可靠性评估流程Fig.5 Flow chart of converter reliability evaluation in wind power system

2 变流器参数对可靠性的影响

由上述分析可知，功率器件的可靠性主要受温度的影响，而根据图4中变流器的热模型，温度的大小取决于器件的损耗、热阻及气温大小，损耗又由变流器的系统参数决定，如负载电流、开关频率和功率因数等[10,14]。器件热阻、气温及负载电流分别由制造工艺、工作环境及风机捕获的功率决定，很难通过人为的因素进行控制；而开关频率、散热条件及功率因数都是可以控制的变量，因此，本文将分别分析这些可控参数对风电变流器可靠性的影响。

2.1 理论分析

（1）器件的开关损耗表达式为[10]

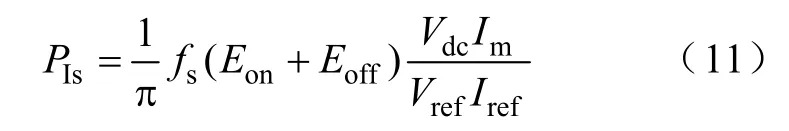
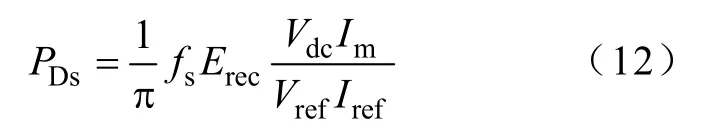
式中，PIs与PDs为IGBT与二极管在一个输出周期内的平均开关损耗；Eon与Eoff为器件 datasheet中IGBT在参考电压Vref、电流Iref下的开通与关断能量损耗；Erec为二极管在Vref及Iref下的反向恢复能量损耗；Vdc为变流器直流侧的电压；Im为每相输入电流的峰值。

当开关频率fs发生变化时，器件的开关损耗会受到影响，以致影响器件的工作温度。开关频率越大，器件的损耗越大，器件的温度及其波动就越大，由式（1）、式（2）可知，这会降低器件的寿命而增大变流器的失效率。

（2）相电流峰值Im的计算式为[14]

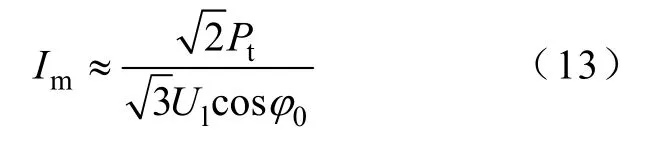
式中，Pt表示风机捕获的功率，大小取决于风速，计算表达式可参考文献[20]；Ul表示变流器交流侧线电压的有效值；φ0为功率因数角。

由于风机输入的有功功率由风速决定，当功率因数 cosφ0变小时，负载峰值电流增大，无功消耗增大，机侧、网侧器件的损耗都会增大，器件的温度也跟着增大而降低变流器的可靠性。

（3）由变流器的简化热模型可知，散热器热阻Rha增大，器件的结温、壳温增大，变流器的失效率也会随着增大。

2.2 实例分析

如图6、图7所示，本文以爱尔兰Dublin测得的2011～2012年风速及气温数据[21]作为评估变流器可靠性的基础，分析验证参数 cosφ0、fs及Rha的变化对变流器可靠性的影响。

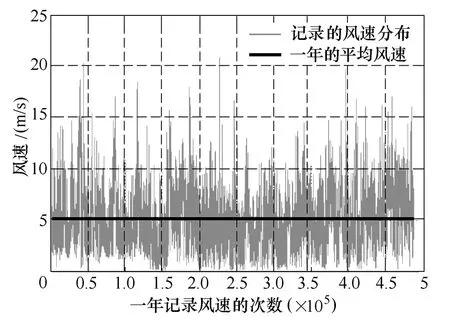
图6 2011～2012年Dublin的风速分布Fig.6 Profile of wind speed in Dublin in 2011～2012

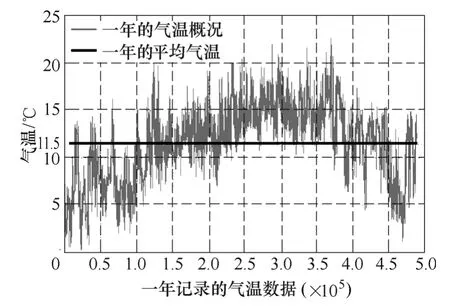
图7 2011～2012年Dublin的气温概况Fig.7 Profile of air temperature in Dublin in 2011～2012

本文所采用的风速数据是每分钟记录一次（一年内共488 153个数据），文献[22]指出，虽然风速在短时间内的变化会较大，然而风电场输出功率在秒与秒之间的变化很小，只有容量的0.1%，而在每分钟之间的变化只有容量的1%，因此，可认为在每分钟内，风机输出的功率同样变化较小，可不考虑风电变流器中器件在此时间内发生温度波动。在不考虑湿度等外界变化对系统可靠性影响的前提下，根据图5所示的变流器可靠性评估步骤，通过一年的风速数据，利用Matlab软件可以统计出一年内器件温度循环的ΔTj、Tm及ΔTc的数值及其次数，并得出相应变流器的每年失效率。

图2中额定功率为1MW的PMSG与变流器中IGBT功率器件的参数分别见表1[10,23]和表2[24]。表1风机运行参数中切入运行风速vcut_in、额定风速vrated及切除停机风速vcut_out的大小由年平均风速确定[23]。

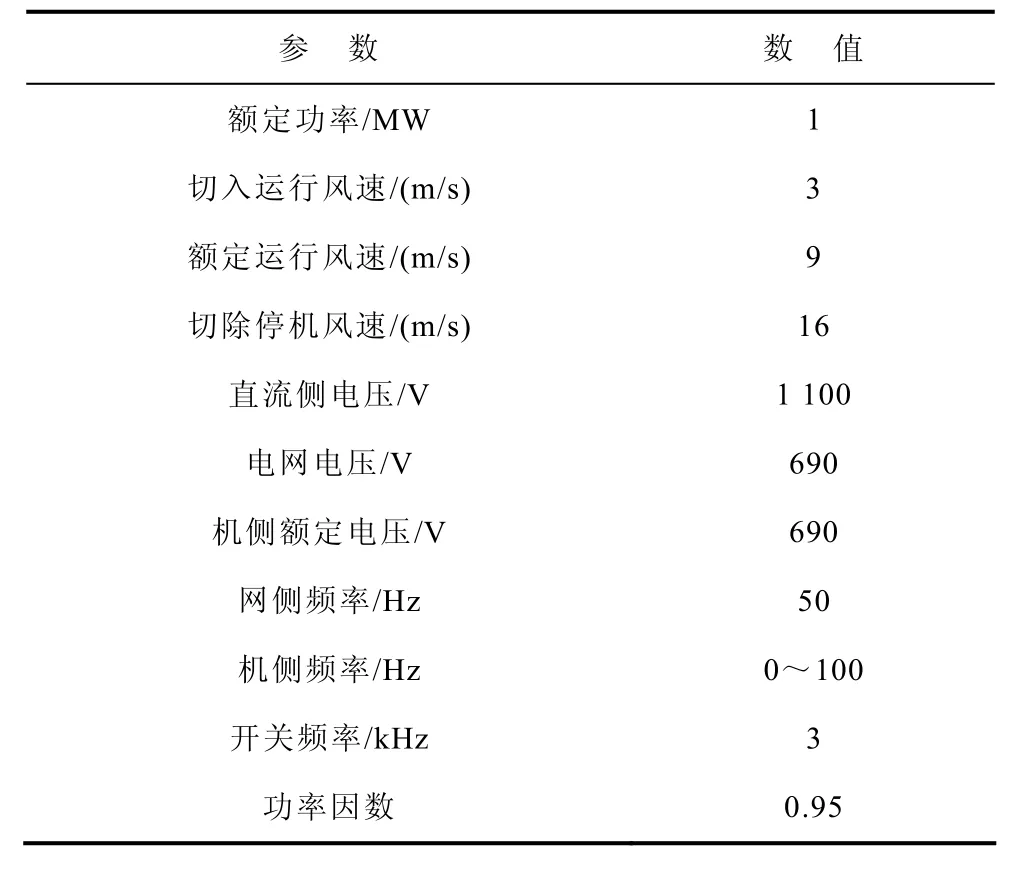
表1 1MW的PMSG风机参数Tab.1 Parameters of 1MW PMSG wind turbine

表2 变流器中IGBT功率器件参数Tab.2 Parameters of IGBT power device in converter

（1）开关频率的影响。开关频率的变化与变流器失效率的关系见表3。从表3可以看出，fs越大，变流器的失效率就越大，由于开关频率越大，器件的开关损耗越大，器件的工作温度及其波动就越大，因此，变流器的失效率越大。当风机以额定输出时，在不同开关频率下，网侧与机侧变流器中器件损耗的变化如图8所示。从图中可以看出，由于开关损耗在总损耗中占的比重较大，当开关频率发生变化时，损耗变化较大，会明显影响器件的温度大小，使得变流器失效率的变化较明显。

表3 开关频率与变流器失效率之间的关系Tab.3 Relationship of switching frequency and converter failure rate

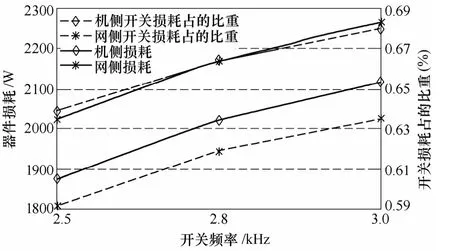
图8 器件损耗与开关频率的关系Fig.8 Relation between component power loss and switching frequency

（2）功率因数的影响。选取功率因数值时，通常选取较高的值，以保证较小的无功消耗。参考我国风电并网要求，无功调节容量应满足功率因数在超前0.95～滞后0.95[25]，当功率因数在此范围内变化时，风电变流器失效率的变化情况见表4。从表4可以看出，当cosφ0变小时，由于变流器损耗增大，器件工作温度幅值及其波动大小变大，于是变流器失效率增大。

表4 变流器的失效率与功率因数的关系Tab.4 Relationship of converter failure rate and power factor

（3）散热器热阻的影响。散热器热阻的变化与变流器失效率的关系见表5。

表5 散热器热阻与变流器失效率之间的关系Tab.5 Relationship of thermal resister of heat sink and converter failure rate

从表5可以看出，Rha越大，变流器的失效率就越大。由于风电变流器的处理功率比较大，使其功率损耗也比较大，于是散热器热阻的微小变化对器件结温、壳温的影响会比较大，以致对变流器失效率的影响也较大。若散热条件设计不当，使得变流器中器件的工作温度过高，会严重降低其可靠性；而若器件温度较低，虽然可以大大降低其失效率，但是需要的散热条件及成本也将大大提升。因此，合理地设计散热条件，对于提高变流器的可靠性乃至优化散热成本至关重要。

3 提高可靠性措施的初步讨论

由式（1）、式（2）可知，变流器的可靠性主要由器件的Tj、ΔTj及ΔTc决定，而且温度波动的影响更大。由于功率因数对变流器可靠性的影响相对比较小，且通常希望变流器以较大的功率因数运行以减小无功消耗，因此可以考虑采用变频或变散热条件的控制方式来降低器件的温度波动，以此来提高变流器的可靠性。

控制的主要思想是在低风速时，增大开关频率或降低散热条件，当风速由低风速变为高风速或由高风速变为低风速时，使得风电变流器中器件的工作温度波动尽量平滑，从而达到提高变流器可靠性的目的。

借鉴风机属性参数的设置需要考虑风速的概况[23]，开关频率或散热条件的改变需要考虑风速的概率分布，以减小切换的频率。Dublin的风速 3～16m/s的概率分布如图9所示。图9中每一个柱状表示风速1m/s内的范围。由图9可以看出，当风速大于5m/s时，风速的概率分布随着风速的增大而减小，这个是由于风速通常集中在低风速，而高风速的较少。因此，若根据风速的大小设置切换点，切换开关频率或散热条件以减小器件的温度波动，那么控制方式的切换设置于越高的风速，如本文风速大于5m/s时，则切换频率的概率就会越低。

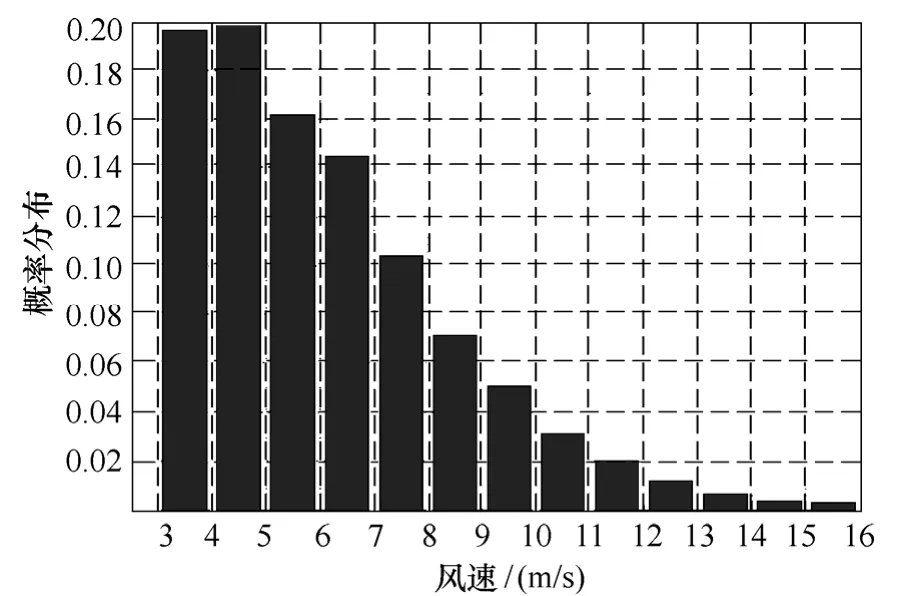
图9 风速3～16m/s的概率分布Fig.9 Distribution of probability of wind speed among 3～16m/s

3.1 改变开关频率的可行性

当切换点设置于8m/s时，开关频率控制为

利用图5中的流程步骤可以统计出当开关频率采用不同值（开关频率分别为3kHz、3kHz与4kHz之间切换、3kHz至5kHz之间切换）时，网侧变流器中器件平均结温Tm、结温变化大小ΔTj与温度循环次数的关系如图10所示。限于篇幅，机侧变流器中三者之间的关系以及壳温的变化趋势本文未给出。

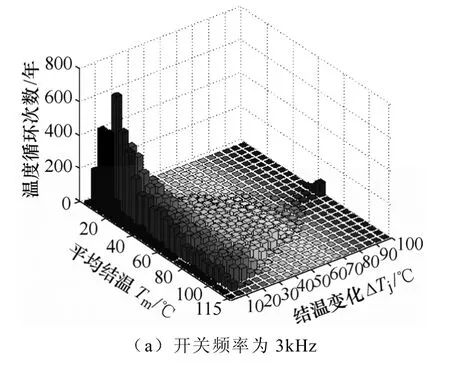
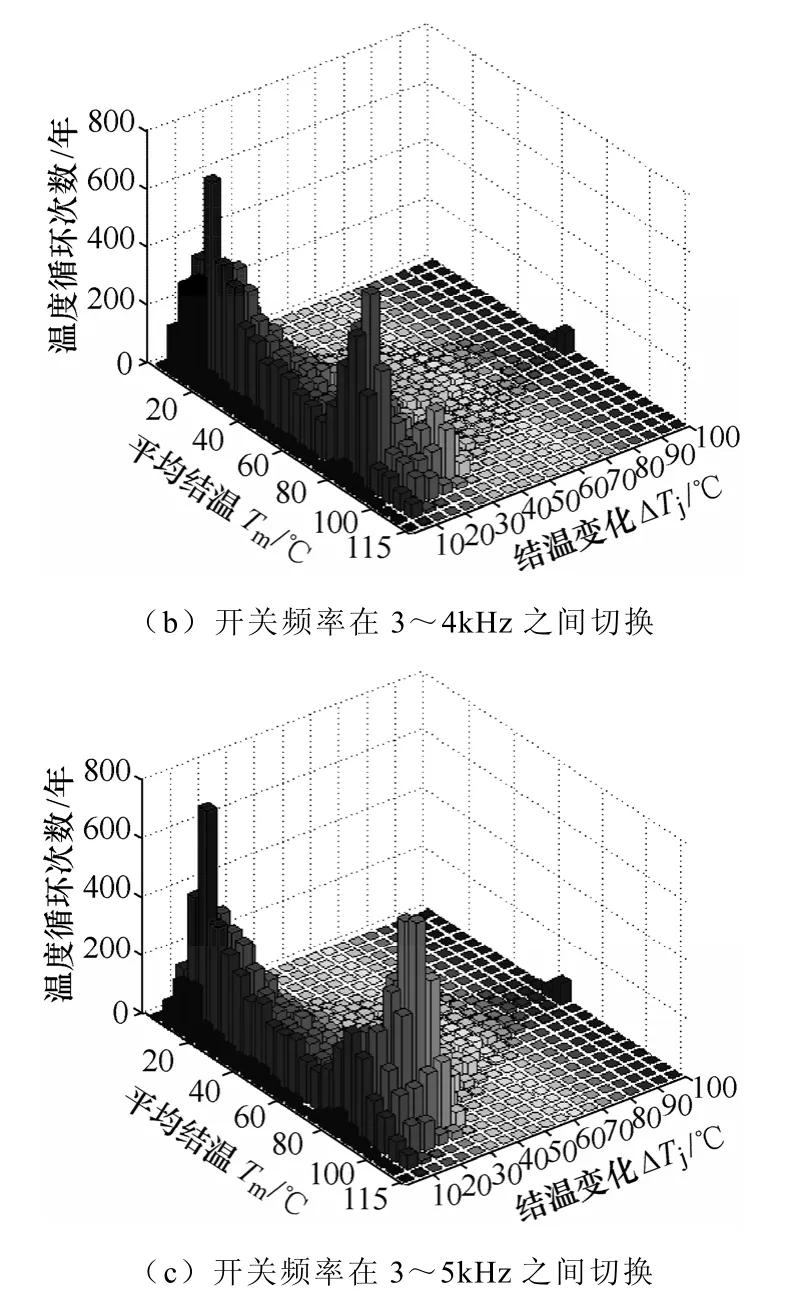
图10 网侧变流器中器件的Tm及ΔTj与温度循环次数之间的关系Fig.10TmandΔTjversus the number of temperature cycles of component in grid side converter

由图10a与图10b的对比可以看出，采用变频的方式，较大的结温波动次数有所减少，反之结温波动较小的次数有所增加，而且对应的平均结温也有所增加，这是由于变频使得大的结温波动变小，低风速采用高开关频率使得平均结温上升，又平均结温对变流器可靠性的影响比温度波动的要小，因此可降低变流器的失效率。

由图10b与图10c的对比可以看出，若低风速采用的开关频率过高，器件开关损耗增大，导致平均结温变大的同时，原来在低风速之间变化而产生较小的结温波动也会变得较大，于是又会使得变流器的失效率开始增大。

当切换点设置于 8m/s时，采用变频与固定开关频率的变流器失效率对比见表6。从表6可以看出，当开关频率在3～5kHz之内切换时，即若风速小于8m/s，开关频率取较大值，若风速超过8m/s，开关频率取值3kHz时，与开关频率为固定的3kHz相比，变流器的失效率有所下降，当开关频率采用 3～4kHz切换时，变流器失效率降低了 0.043 9，即降低了20.7%。

表6 变频与固定开关频率下的变流器失效率对比Tab.6 Comparison of converter failure rate under changeable and fixed switching frequency

因此，适当地采用变频的控制方式，可有效提高变流器的可靠性，而且据风速的分布概率，合理选择开关频率的切换点，也可尽可能减小切换频率以降低对系统的影响。本节的分析结论表明了通过改变开关频率来提高可靠性的可行性，但具体的优化策略还需深入的研究和分析。

3.2 改变散热条件的可行性

同样，改变散热条件，即改变散热热阻，也要考虑风速的概率分布。当切换点设置于8m/s时，采用变散热热阻与固定散热热阻的变流器失效率对比见表7。

表7 变热阻与固定散热热阻下的变流器失效率对比Tab.7 Comparison of converter failure rate under changeable and fixed heat sink resistance

从表7可以看出，当若风速小于8m/s，散热热阻选择较大的值，而风速超过8m/s，散热热阻选择较小的值（4.2℃/kW）时，与散热热阻固定为4.2℃/kW相比，变流器的失效率有所下降，最大可降低0.038 7，即降低了18.2%。因此，采用变散热条件的控制方式，同样也可有效提高变流器的可靠性。散热热阻改变的可行性取决于其变化的快慢，如果要求太快则难于实现，文献[26]针对汽车变流器，研究表明变散热条件可实现对变流器可靠性的控制，汽车变流器温度波动速率与风电变流器中器件温度波动的时间数量级接近（数分钟之内），因此，变散热条件的控制方式同样适用于风电变流器。同样，如何优化控制散热条件还需更深入的研究。

4 结论

分别根据器件温度幅值及其波动对变流器可靠性的影响机理，综合考虑铝键合线失效与焊料层失效，给出了风电变流器功率器件的可靠性评估模型。结合实际的风速及气温数据，分析论证了风电变流器的系统参数——功率因数、开关频率及散热器热阻的变化对变流器可靠性的影响。结果表明，开关频率与散热热阻对变流器可靠性的影响比较大。根据分析结果，本文初步探讨了通过改变开关频率以及散热条件方式来提高可靠性的可行性。分析结果表明，在低风速时增大开关频率或降低散热条件，以降低大的温度幅值变化，可达到提高变流器可靠性的目的。同时，在设置变频或变散热条件的切换位置时考虑了风速的分布概况以减小切换次数，从而降低控制方式的切换对系统的影响。对于开关频率和散热条件的优化选择和控制将是下一步的研究重点。

[1] Blaabjerg F,Liserre M,Ke Ma.Power electronics converters for wind turbine systems[J].IEEE Transactions on Industry Applications,2012,48(2):708-719.

[2] Spinato F,Tavner P,van Bussel G J W,et al.Reliability of wind turbine subassemblies[J].IET Renewable Power Generation,2009,3(4):387-401.

[3] Boettcher M,Fuchs F W.Power electronic converters in wind energy systems considerations of reliability and strategies for increasing availability[C].Conference on Power Electronics and Applications(EPE),Birmingham,United Kingdom,2011:1-10.

[4] 孔学东,恩云飞.电子元器件失效分析与典型案例[M].北京:国防工业出版社,2006.

[5] Held M,Jacob P,Nicoletti G,et al.Fast power cycling test of IGBT modules in traction application[C].International Conference on Power Electronics and Drive Systems,Singapore,1997,1:425-430.

[6] Aten M,Towers G,Whitlry C,et al.Reliability comparison of matrix and other converter topologies[J].IEEE Transactions Aerospace and Electronic Systems,2006,42(3):867-875.

[7] Abdi B,Ranjbar A H,Gharehpetian G B,et al.Reliability consideration for parallel performance of semiconductor switches in high-power switching power modules[J].IEEE Transactions on Industrial Electronics,2009,56(6):2133-2139.

[8] Burgos R,Chen Gang,Wang F,et al.Reliabilityoriented design of three-phase power converters for aircraft applications[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(2):1249-1263.

[9] Arifujjaman M,Iqbal M T,Quaicoe J E.A comparative study of the reliability of the power electronics in grid connected small wind turbine systems[C].Conference on Electrical and Computer Engineering(ECE),Newfoundland,Canada,2009:394-397.

[10] Xie Kaigui,Jiang Zefu,Li Wenyuan.Effect of wind speed on wind turbine power converter reliability[J].IEEE Transactions on Energy Conversion,2012,27(1):96-104.

[11] Lutz J,Schlangenotto H,Scheuermann U,et al.Semiconductor power devices-physics,characteristics,reliability[M].Heidelberg:Springer,2011.

[12] Ciappa M.Selected failure mechanisms of modern power modules[J].Microelectronics Reliability,2002,42(4-5):653-667.

[13] IGBT Modules Application Manual[EB/OL].Fuji Electric Co.,Ltd.2011.[2013-2-1].http://www.fujielectric.com/products/semiconductor/technical/ap plication/box/doc/REH984b/REH984b_a.pdf.

[14] Wei Lixiang,Kerkman R J,Lukaszewski R A.Evaluation of power semiconductors power cycling capabilities for adjustable speed drive[C].IEEE Industry Applications Society(ISA)Annual Meeting,Alberta,Canada,2008:1-10.

[15] Reliability Methodology for Electronic Systems[G].FIDES guide 2009,May,2009.

[16] 孙青,庄亦琪,王锡吉,等.电子元器件可靠性工程[M].北京:电子工业出版社,2002.

[17] Hirschmann D,Tissen D,Schröder S,et al.Reliability prediction for inverters in hybrid electrical vehicles[J].IEEE Transactions on Power Electronics,2007,22(6):2511-2517.

[18] 杜毅,廖美英.逆变器中 IGBT模块的损耗计算及其散热系统设计[J].电气传动自动化,2011,33(1):42-46.

Du Yi,Liao Meiying.Loss calculation of IGBT module and heat dissipation system design of inverters[J].Electric Drive Automation,2011,33(1):42-46.

[19] Arifujjaman M,Iqbal M T,Quaicoe J E.Power electronics reliability comparison of grid connected small wind energy conversion systems[J].Wind Engineering,2011,35(1):93-110.

[20] Jangamshetti,S H,Rau V G.Site matching of wind turbine generators:a case study[J].IEEE Transactions on Energy Conversion,1999,14(4):1537-1543.

[21] Dun laoghaire harbor company[EB/OL].2012[2012-12-1].http://www.dlharbour.ie/.

[22] Wan Y H.Wind power plant behaviors:analyses of long-term wind power data[R].National Renewable Energy Laboratory,Colorado,2004.http://www.osti.gov/bridge/.

[23] Fox B,Flynn D,Bryans L,et al.Wind power integration connection and system operational aspects[M].London:The Institution of Engineering and Technology,2007.

[24] FUJI Electric IGBT Module datasheet,1MBI1600U4C-170[EB/OL].2012[2012-12-1].http://semiconductor.jonweb.net/images/artical/fuji/1MBI1600U4C-170.pdf

[25] GB/T—200中华人民共和国国家标准[S].

[26] Wang Xiang,Castellazzi A,Zanchetta P.Regulated cooling for regulated thermal cycling of power devices[C].The 7th IEEE International Power Electronics and Motion Control Conference,Harbin,2012:238-244.