锁相环对多端柔性直流稳定性作用分析及参数选择研究

熊凌飞 韩民晓 姚蜀军

（华北电力大学新能源电力系统国家重点实验室 北京 102206）

0 引言

近年来，随着风电、光电等可再生能源的快速发展，传统两端柔性直流输电（VSC-HVDC）的接入形式难以满足需求。为了提高系统的灵活性、可靠性，实现多电源多落点的供电形式，多端直流输电（VSC-MTDC）逐渐受到了广泛的关注[1,2]。电压源型换流器（VSC）能够实现有功功率与无功功率的解耦控制，潮流反转不需要改变电压极性，且随着多电平换流器的发展，损耗与谐波含量明显下降[3]，这使得 VSC在构建多端系统时具有独特的技术优势[4]，因而VSC-MTDC在可再生能源接入、城市供电等诸多领域具有广阔的应用前景。

目前，大量文献对 VSC-MTDC的电磁暂态模型[5,6]、控制系统[7-10]和保护[11]做了相应的研究。文献[12,13]建立了两端VSC-HVDC的小信号模型，但并未考虑多端直流系统换流站间的相互作用。文献[14-16]针对换流站间的协调控制进行了分析，包括常用的电压倾斜控制及电压裕度控制等方式，但未涉及控制系统参数对直流系统稳定性的影响。文献[17,18]建立了 VSC-MTDC的小信号模型，但只进行了时域的仿真对比，未从稳定性方面进行分析。文献[19,20]在频域下分析了系统的稳定性，但文中没有考虑锁相环（PLL）对系统的影响。PLL作为控制系统中的重要组成部分，对系统稳定性影响不能忽略，本文将对其进行详细分析。

小信号稳定性分析是直流系统控制器设计的重要方法。状态空间方程能够准确描述直流系统的动态过程，同时可以在频域下分析系统的稳定性。直流电压作为VSC-MTDC最重要的控制目标，系统的稳定性通常表现为直流电压的稳定控制。而根轨迹曲线可以通过主导极点在坐标系中的位置直观地反映这一点。

本文首先基于状态空间方程建立了三端 VSCMTDC的小信号模型，主要包括4部分：换流器、控制系统（测量环节、内环/外环、锁相环）、交流系统及直流线路。本文中采用标幺值系统，即各电气量与控制器所需信号均为标幺值，因此可根据不同的应用场合，按照需求选取基准值，进而达到实际要求。这使得模型更具有通用性，同时各部分均为模块化建模，具有扩展性。为验证模型的正确性，文中将其与基于 PSCAD/EMTDC建立的电磁暂态模型进行时域的比对验证。最后采用根轨迹的方法，详细分析了 PLL、内环/外环的参数对 VSC-MTDC稳定性的影响，并指出PLL对其影响不能忽略，最后确定了各参数的稳定范围。

1 小信号模型

图1所示为文中建立的VSC-MTDC拓扑结构，其包含3个换流站，其中换流站1为送端，换流站2、3为受端。

图1 三端柔性直流输电系统Fig.1 Three-terminal VSC system

如前文所述，本文采用标幺值系统[21]，各电气量在额定情况下均为1.0(pu)，且由于交流系统的阻抗角典型范围在 70°～85°[22]。因此，文中设定三端接入的交流系统等效电压均为180∠°。本节将以此为例，推导VSC-MTDC的小信号模型。

图2所示为一端VSC接入交流系统的典型拓扑结构。可以看到，控制系统通过对换流器的精确快速控制，将三相交流电压转换为直流量注入直流线路中。而在该过程中，PLL为交/直流间的变换提供PCC点电压Vt的相位信息θ。

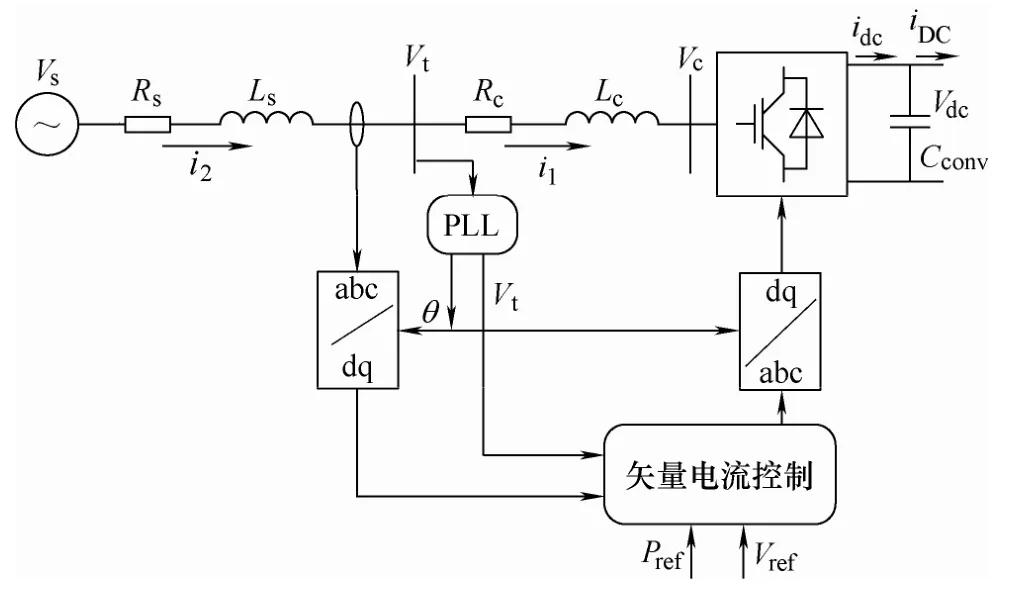
图2 典型一端柔性直流输电系统Fig.2 Typical 1-terminal VSC system

1.1 PLL

PLL是VSC-MTDC的重要组成部分，该环节为控制系统的坐标变换提供相位信息，也即为换流器输出的交流电压提供相位上的参考点。因此，PLL的动态特性直接决定了整个 VSC-MTDC的运行特性。现有文献通常认为PLL的动态特性在暂态过程中变化较慢，因而可以忽略PLL对VSC- MTDC暂态特性的影响。而下文将建立PLL的详细数学模型，并证明 PLL的动态特性对整个交/直流系统的稳定性有着不可忽视的影响。

PLL的典型结构如图3所示。文献[23,24]对PLL的建模均基于 αβ坐标系，导致PLL输入的误差信号运算复杂，不利于线性化。

图3 锁相环典型结构Fig.3 Typical structure of PLL

由图3可知，PLL是一个闭环控制系统，其非线性通常难以处理。本文采用dq坐标系，以公共连接点（PCC）电压Vt的q轴分量Vtq作为PLL的输入，由于Vtq为状态变量，其大小受输出角度θ影响，因而实现了 PLL的闭环，特征矩阵具体形式可见附录。本文选取xPLL_1与xPLL_2为状态变量，分别描述PLL中比例积分器与积分环节。

可将式（1）和式（2）写为

式中，Vtq为PCC点电压Vt的q轴分量；θ为PLL输出相角；Kp_PLL、Ki_PLL为PLL中的PI参数。

1.2 换流器

换流器的主要作用在于实现交流侧与直流侧间的功率交换，由此在忽略损耗的情况下可以得到（本文采用等功率Park变换）

式中，Vcd、Vcq、i1d、i1q分别为换流器输出电压Vc与输出电流i1的dq分量；Vdc、idc分别为直流电压与直流电流。

又因为

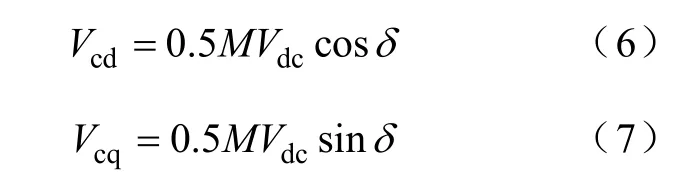
将式（6）、式（7）代入式（5）可得

式中，δ为Vt与Vc间的相位差；M为换流器调制比。

对换流器的直流电容可列出方程

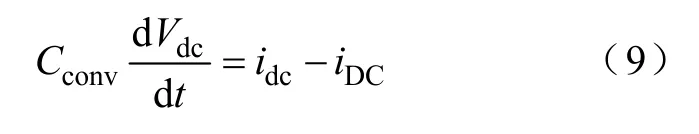
由此，式（5）～式（9）可用于描述换流器，对于交流侧而言，换流器等效为电压源，输出电压Vc；而对于直流侧，换流器等效为电流源，输出电流idc。

1.3 控制系统

本文采用目前最为通用的矢量电流控制作为VSC控制器，主要包括测量环节、外环控制器、内环控制器及PLL等4部分。本文1.1节中已经完成PLL的建模，因此，本节将对另外3部分进行模型的详细推导。

1.3.1测量环节

为了尽可能让模型接近实际系统，本文对测量环节也进行了建模，并将其等效为一阶系统，传递函数为

式中，Vtd、Vtq分别为Vt的dq分量；Tmvd、Tmvq、Tmid、Tmiq分别为Vt与i1的dq分量测量环节时间常数；Tmvdc为直流电压Vdc的测量环节时间常数。

由传递函数可得到状态空间方程的形式（能控标准型）[25]

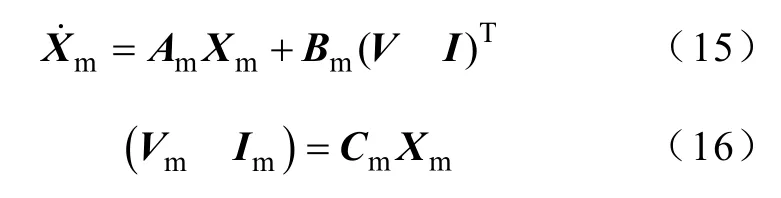
其中

下文中，控制系统所需的电气量均为经过测量环节后的数值，并用下标m表示。

1.3.2外环控制器

外环控制器可分为有功功率类控制（定有功功率控制、定直流电压控制及定频率控制）与无功功率类控制（定交流电压控制、定无功功率控制）。定频率控制常用于无源系统，本文暂不考虑。每个换流站只能在这两类控制中各选其一。在 VSC-MTDC中，通常只有1个换流站采用定直流电压控制，余下的换流站均为定有功功率控制，其中，采用定直流电压控制的换流站具有平衡功率的作用。

控制系统具体结构如图4所示，图中Aref、Bref分别为有功功率类控制及无功功率类控制指令值。

图4 VSC控制系统Fig.4 VSC control system

由图4可以得到定有功功率控制

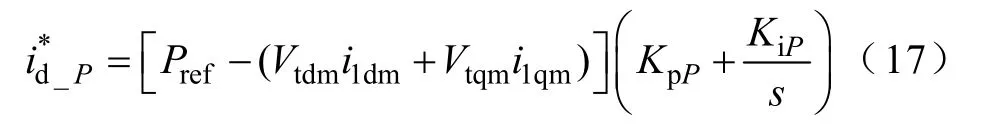
定直流电压控制

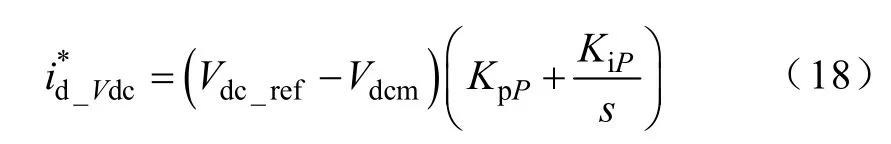
定交流电压控制

定无功功率控制

式中，Vt_LN_peak_ref为交流电压指令值（相电压峰值）；Vref为交流电压指令值（线电压有效值）；KpP、KiP、KpQ及KiQ分别为外环控制器有功功率类及无功功率类回路的PI参数。

由式（17）～式（20）可以得到其状态空间方程的能控标准形式为

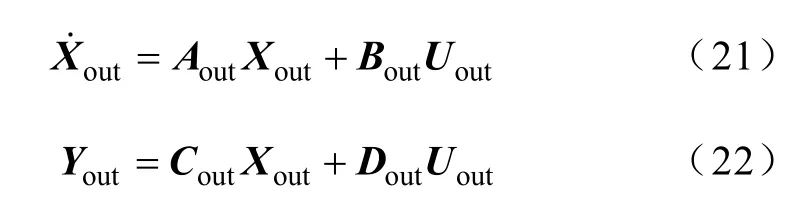
其中，定有功功率控制

定直流电压控制

定交流电压控制

定无功功率控制

1.3.3内环控制器

内环控制器结构如图4所示，包含3部分：比例积分环节、耦合补偿量ωL及前馈Vtdm、Vtqm，其输入为外环控制器的输出id*、iq*分别与测量值i1dm、i1qm的差值，描述方程为

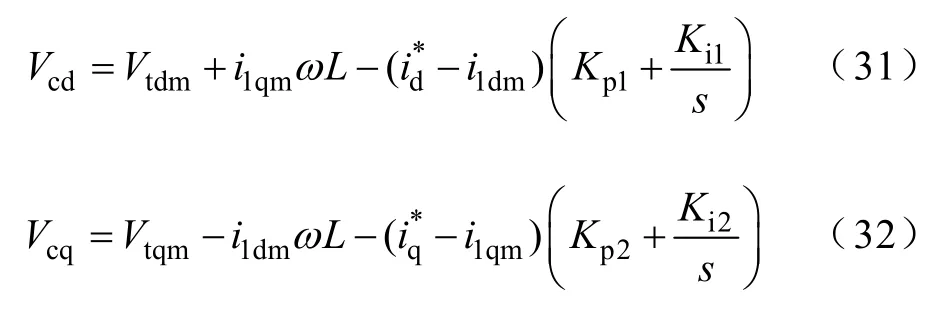
式中，Kp1、Ki1、Kp2及Ki2分别为内环控制器有功分量及无功分量回路的PI参数。

同样，将其写为状态空间方程形式（外环分别采用定有功功率控制及定交流电压控制）为

其中

式（35）和式（36）分别对应有

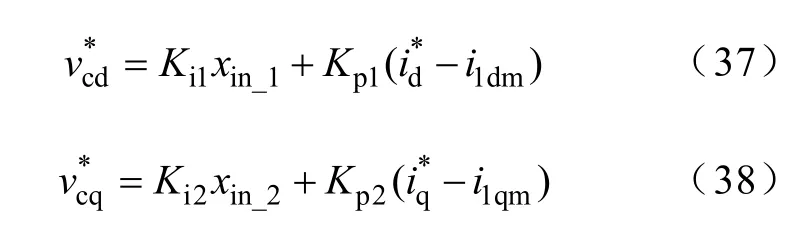
1.4 直流线路

为简化分析，本文对直流线路采用π形等值，建立了三端VSC-MTDC的线路模型，如图5所示，图中C1、C2、C3为各换流站电容与线路电容合并之后的等效电容。

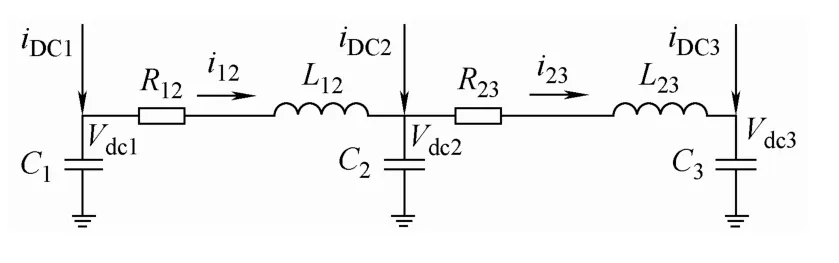
图5 三端直流系统线路模型Fig.5 Model of three-terminal DC line

由图5可知，直流线路可由如下方程描述

其中

式中，33×I为三阶单位矩阵；矩阵T用以描述直流侧的电流参考方向，且以流出为正。

1.5 交流系统

交流系统在 dq旋转坐标系下的动态方程为（交流侧以流入换流器为正方向）

由于式（41）～式（43）中，Vsd、Vsq、Vcd及Vcq不是状态变量，需要用状态变量代替。假设α为交流系统戴维南等效电压对 PCC点电压Vt（假定∠Vt=0°）的初始相角，而θ为PLL的输出相角，则Vsd、Vsq可写为

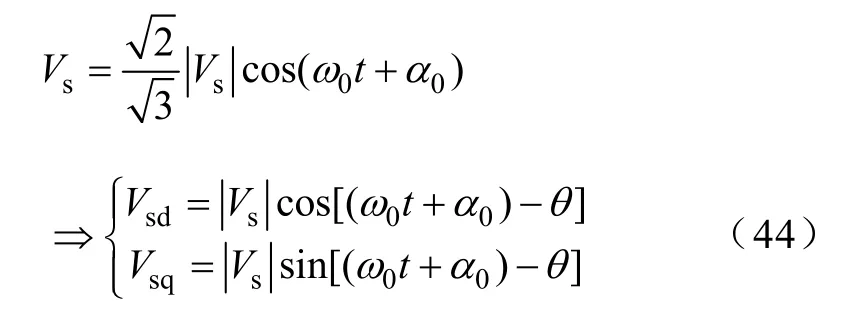
在换流器为定有功功率控制/定交流电压控制时，联立式（3）、式（4）、式（6）～式（9）、式（16）、式（17）、式（22）～式（34）和式（35），可得

特征矩阵具体形式见附录。

2 模型验证

上文详细推导了三端VSC-MTDC小信号模型。为验证其正确性，本节在 PSCAD/EMTDC中建立了相应的电磁暂态模型，并将二者在时域下进行比对验证。

本文所用 VSC-MTDC拓扑如图 1所示，其电气参数见表1。

表1 各换流站的电气参数Tab.1 Parameters of main circuit of converters

图6 小信号模型及电磁暂态模型时域比对Fig.6 Comparation of small signal model with EMTDC model in time domain

图6为VSC-MTDC在受到小扰动情况下，本文所建小信号模型及电磁暂态模型的比对结果。本文分别在两个端子上设定扰动，分别为VSC3的直流电压指令Vdc_ref在t=4.15s时发生ΔVdc_ref=−0.1（pu）的阶跃并于t=6.15s时恢复；于此同时，VSC2的有功功率指令Pref在t=5.15s时发生ΔPref=−0.1（pu）的阶跃，并同样于t=6.15s时恢复。

图6a～图6c分别为VSC1、VSC2及VSC3的有功功率P，PCC点交流电压Vt及直流电压Vdc的动态响应曲线。可以看到，EMTDC波形（电磁暂态模型）与SmallSignal波形（小信号模型）几乎完全重合，验证了模型的正确性。

3 稳定性分析

在小信号模型得到验证之后，本节将分析控制系统参数对VSC-MTDC稳定性的影响。限于篇幅，本文将只分析换流站1参数对系统稳定性的影响。其余端子可根据各自的控制方式采用 1.3节中对应的状态方程进行分析。

本节将通过对PLL、外环控制器及内环控制器3部分的参数分析，得到VSC-MTDC的根轨迹曲线。其中，主回路与控制系统参数分别见表1和表2。

表2 各换流站的控制系统参数Tab.2 Parameters of control system of converters

图7 多端直流系统随锁相环PI参数增大的根轨迹曲线Fig.7 Root locus of VSC-MTDC as the increase of PI parameters of PLL

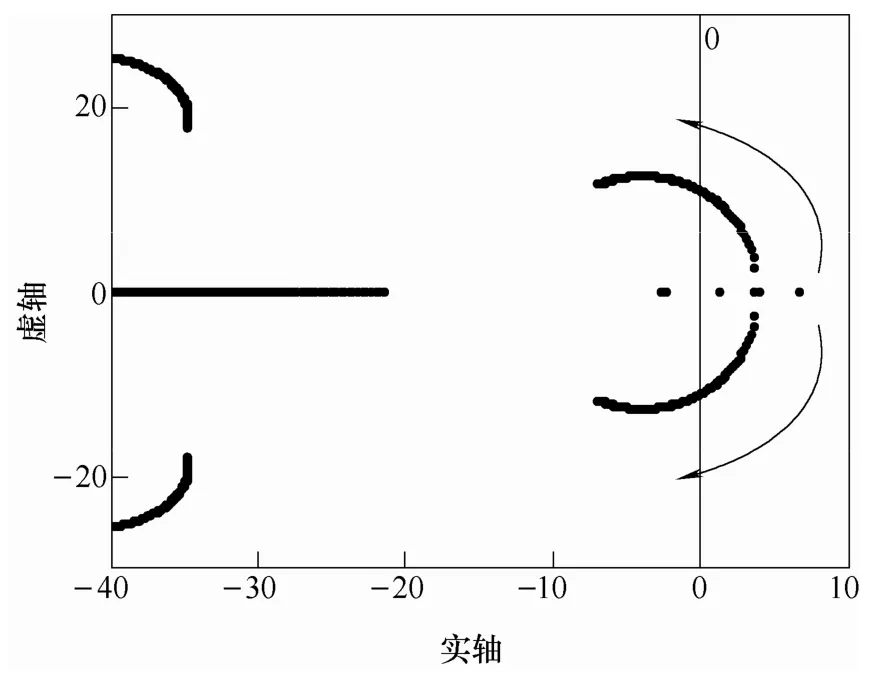
图8 多端直流系统随外环无功分量PI参数增大的根轨迹曲线Fig.8 Root locus of VSC-MTDC as the increase of PI parameters of outer loop(reactive component)

图9 多端直流系统随内环有功分量PI参数增大的根轨迹曲线Fig.9 Root locus of VSC-MTDC as the decrease of PI parameters of inner loop(active component)

图7～图9分别为VSC-MTDC主导极点在PLL、外环无功控制回路及内环有功控制回路参数变化而得到的根轨迹曲线。为了简化分析，参数变化时，比例积分参数均保持固定的比例：锁相环参数（Ki=2.5Kp，Kp=1～200），外环参数（Ki=100Kp，Kp=0.01～2），内环参数（Ki=50Kp，Kp=0.01～10）。

可以看到，PLL在Kp较小时，主导极点接近坐标系原点；随着Kp的增大，极点开始逐渐远离Y轴并向左半平面移动；但Kp的进一步增大，使得系统稳定裕度再次减小，当Kp＞100时，极点进入坐标系右半平面，即系统失去稳定。

外环无功分量控制回路的PI参数较小时，主导极点处于右半平面；随着Kp的增大，系统主导极点逐渐进入坐标轴左半平面，即系统趋于更加稳定。

同样，随着内环有功分量控制回路的PI参数的增大，系统主导极点进入左半平面，系统进入稳定运行状态。

由此，在 VSC-MTDC模型的建立中，可以根据控制系统各部分根轨迹曲线的变化趋势，确定各自参数选取范围，以提高整个系统的稳定性。

同时，本文在对外环有功功率分量控制回路及内环无功功率分量控制回路PI参数进行根轨迹分析时，由于参数在大范围变化下，主导极点在坐标系中并未出现较大的移动，即这两部分的参数对系统稳定性的影响相对较小，由此文中未列出其根轨迹曲线。

4 结论

本文首先建立了 VSC-MTDC的小信号模型。文中将系统划分为4部分，并分别列出了各部分的状态空间方程，其中包括：换流器及其控制系统（测量环节、外环/内环、PLL）、交流系统及直流线路。其次，本文基于PSCAD/EMTDC建立了VSC-MTDC相应的电磁暂态模型，在时域下，通过比对两个模型在遭受小扰动下的暂态波形，验证了小信号模型的正确性。最后，文中分别对PLL、外环及内环控制参数进行了频域分析，得到各自的根轨迹曲线。可以看到，除去现有文献中分析的内/外环控制器参数外，PLL的参数选取对整个交/直流系统稳定性的影响也极大，因此在对 VSC-MTDC的稳定性分析中不能忽略。

本文建立了 VSC-MTDC研究的模型平台，采用标幺值系统，模块化建模等方式，使其具有通用性及可扩展性，同时文中给出的参数稳定范围具有一般性。

附录A矩阵（16×16阶）

因篇幅原因，仅列出换流站1（外环控制为定有功功率/定交流电压控制）的特征矩阵，直流线路矩阵参见本文式（39）。

[1] 李响,韩民晓.海上风电串联多端VSC-HVDC协调控制策略[J].电工技术学报,2013,28(5):42-48,57.

Li Xiang,Han Minxiao.A coordinated control strategy of series multi-terminal VSC-HVDC for offshore wind farm[J].Transactions of China Electrotechnical Society,2013,28(5):42-48,57.

[2] 陈霞,林卫星,孙海顺,等.基于多端直流输电的风电并网技术[J].电工技术学报,2011,26(7):60-67.

Chen Xia,Lin Weixing,Sun Haishun,et al.LCCMTDC technology for wind farms integration[J].Transactions of China Electrotechnical Society,2011,26(7):60-67.

[3] Gemmell B,Dorn J,Retzmann D,et al.Prospects of multilevel VSC technologies for power transmission[C].IEEE/PES Transmission and Distribution Conference and Exposition,2008:1-16.

[4] 汤广福,贺之渊,庞辉.柔性直流输电工程技术研究、应用及发展[J].电力系统自动化,2013,37(15):3-14.

Tang Guangfu,He Zhiyuan,Pang Hui.Research,application and development of VSC-HVDC engineering technology[J].Automation of Electric Power Systems,2013,37(15):3-14.

[5] Van der Meer A A,Hendriks R L,Kling W L.Combined stability and electro-magnetic transients simulation of offshore wind power connected through multi-terminal VSC-HVDC[C].IEEE Power and Energy Society General Meeting,Minneapolis,2010:1-7.

[6] Liu S,Xu Z,Hua W,et al.Electromechanical transient modeling of modular multilevel converter based multiterminal HVDC systems[J].IEEE Transactions on Power Systems,2013,29(1):72-83.

[7] 吴俊宏,艾芊,章健,等.基于多代理技术的VSC-MTDC控制系统[J].电力系统自动化,2009,33(19):85-89.

Wu Junhong,Ai Qian,Zhang Jian,et al.A VSC-MTDC control system based on multi-agent technology[J].Automation of Electric Power Systems,2009,33(19):85-89.

[8] 朱瑞可,李兴源,应大力.VSC-MTDC互联系统频率稳定控制策略[J].电网技术,2014,38(10):2729-2734.

Zhu Ruike,Li Xingyuan,Ying Dali.A frequency stability control strategy for interconnected VSC-MTDC transmission system[J].Power System Technology,2014,38(10):2729-2734.

[9] 罗永捷,李耀华,王平,等.多端柔性直流输电系统下垂控制P-V特性曲线时域分析[J].电工技术学报,2014(S1):408-415.

Luo Yongjie,Li Yaohua,Wang Ping,et al.Timedomain analysis of P-V characteristic for droop control strategy of VSC-MTDC transmission system[J].Transactions of China Electrotechnical Society,2014(S1):408-415.

[10] 郭春义,赵成勇,王晶.新型双馈入直流输电系统供电无源网络的运行特性研究[J].电工技术学报,2012(11):211-218.

Guo Chunyi,Zhao Chengyong,Wang Jing.Operation characteristic research on novel double-infeed HVDC system supplying passive network[J].Transactions of China Electrotechnical Society,2012(11):211-218.

[11] Tang L,Ooi B T.Protection of VSC- multi-terminal HVDC against DC faults[C].IEEE 33rd Annual Power Electronics Specialists Conference,2002,2:719-724.

[12] 郑超,周孝信.基于电压源换流器的高压直流输电小信号动态建模及其阻尼控制器设计[J].中国电机工程学报,2006,26(2):7-12.

Zheng Chao,Zhou Xiaoxin.Small signal dynamic modeling and damping controller designing for VSC based HVDC[J].Proceedings of the CSEE,2006,26(2):7-12.

[13] Padiyar K R,Prabhu N.Modelling,control design and analysis of VSC based HVDC transmission systems[C].2004 International Conference on Power System Technology,2004,1:774-779.

[14] 陈海荣,徐政.适用于VSC-MTDC系统的直流电压控制策略[J].电力系统自动化,2006,30(19):28-33.

Chen Hairong,Xu Zheng.A novel DC voltage strategy for VSC multi-terminal HVDC system[J].Automation of Electric Power System,2006,30(19):28-33.

[15] Beerten J,Belmans R.Modeling and control of multiterminal VSC HVDC systems[J].Energy Procedia,2012,24(10):123-130.

[16] Dierckxsens C,Srivastava K,Reza M,et al.A distributed DC voltage control method for VSC MTDC systems[J].Electric Power Systems Research,2012,82(1):54-58.

[17] Cole S,Beerten J,Belmans R.Generalized dynamic VSC MTDC model for power system stability studies[J].IEEE Transactions on Power Systems,2010,25(3):1655-1662.

[18] Beerten J,Cole S,Belmans R.Modeling of multiterminal VSC HVDC systems with distributed DC voltage control[J].IEEE Transactions on Power Systems,2013,99:1-9.

[19] Kalcon G O,Adam G P,Anaya-Lara O,et al.Smallsignal stability analysis of multi-terminal VSC-based DC transmission systems[J].IEEE Transactions on Power Systems,2012,27(4):1818-1830.

[20] Chaudhuri N R,Majumder R,Chaudhuri B.System frequency support through multi-terminal DC(MTDC)grids[C].IEEE Power and Energy Society General Meeting(PES),2013:1-1.

[21] Yazdani A,R Iravani.Voltage-sourced con- verters in power systems[M].New Jersey:John Wiley & Sons,2010.

[22] IEEE Standards Board.IEEE Std 1204—1997,IEEE Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities[S].1997.

[23] Jovcic D,Pahalawaththa N,Zavahir M.Analytical modelling of HVDC-HVAC systems[J].IEEE Transactions on Power Delivery,1999,14(2):506-511.

[24] Karawita C.HVDC interaction studies using small signal stability assessment[D].Winnipeg:Univeristy of Manitoba,2009.

[25] 胡寿松.自动控制原理[M].北京:科学出版社,2007.