电网不对称时抑制负序电流并网逆变器的控制策略
姜卫东 吴志清 李王敏 佘阳阳 胡 杨
(合肥工业大学电气与自动化工程学院 合肥 230009)
0 引言
并网型逆变器随着分布式发电系统的发展得到了越来越广泛的应用,如何有效地控制光伏并网逆变器的输出电流,尽量减少对电网的谐波污染成为光伏并网的关键技术之一。在实际系统中,电网电压不对称的情况普遍存在,若不采取不平衡补偿,则会在并网逆变器的直流侧产生偶次、在交流侧产生奇次非特征谐波,对电网产生污染,使逆变器的性能恶化,严重时甚至可能烧毁设备[1-3]。
电网不对称下控制目标主要有抑制负序电流或抑制直流侧波动两种,衍生的控制策略有很多。文献[4,5]中所提出的双 d、q控制算法需要对电网电压、反馈电流进行正、负序分离,但现行的分离方法主要利用滤波器或T/4延时算法[6],给控制系统带来了不容忽视的延时和误差。文献[7-9]采用比例谐振(PR)控制器在两相静止坐标系中实现了电流的无静差控制,但 PR控制器的分析和设计较为复杂。文献[11,12]将非线性控制理论应用到电网不对称时整流器的控制策略中。文献[11]中电流内环采用内模控制器的不平衡控制策略,实现了正、负序电流的无差控制,系统获得了较强鲁棒性;文献[12]应用了无源控制理论,收到了良好的效果,其本质上是一种非线性控制策略。但非线性控制器对参数的依赖性大,且需要全状态可测量。
本文首先提出一种基于电压瞬时值的正、负分离方法,并利用交流遗忘积分算法对分离信号滤波,实现了延时小、准确度高的特性。然后以抑制负序电流为控制目标,在正序和负序同步旋转坐标下实现并网电流的控制, 使逆变器输出的电压与电网电压达到一致,输出三相正弦对称电流。
1 电网不对称时的数学模型
1.1 逆变器的数学模型

图1 并网逆变器结构图Fig.1 The diagram of grid inverter
图 1为三相电压型并网逆变器主电路拓扑结构。由于无中性点连接,不存在零序电流回路,忽略零序电压的影响。当电网电压不平衡时,电网电压矢量可表示为正序电压矢量和负序电压矢量之和,即

式中,ω为电网电压角频率;分别为dq坐标系下的正、负序电网电压复矢量;Eαβ分别为 αβ坐标系下的电网电压复矢量。其中,上标+、-分别表示正、负序分量。同理,三相逆变器输出交流电压复矢量Vαβ、输出交流电流复矢量Iαβ可表示为

并网逆变器在αβ坐标系下模型方程为

式中,L为交流滤波电感;R为滤波电感的寄生电阻。当电网不平衡时,结合式(1)~式(3),在dq坐标系下正、负序矢量方程可表示为

1.2 功率分析
图2所示为电网电压定向图。图中,d+和q+为正序旋转坐标系d、q轴,以角速度ω逆时针旋转;d-和q-为负序旋转坐标系d、q轴,以角速度ω顺时针旋转;δ为正、负电压矢量间的相位差,一般可认为δ=2ωt+ξ,由于电网电压不平衡情况很多,因此正、负序的初始角取值不相等且不固定,ξ表示正、负序初始角的差值。

图2 不对称时电网电压定向图Fig.2 Directed graph of grid voltage based on asymmetric grid
有功量可表示为任意电压和电流的点乘积,即
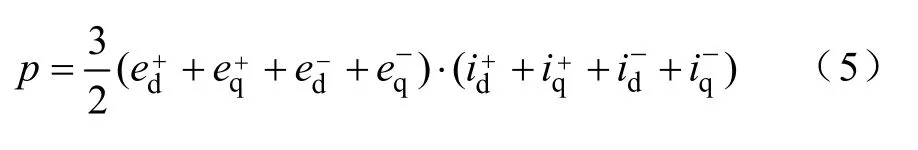
无功量可表示为任意电压和电流的叉乘积,即
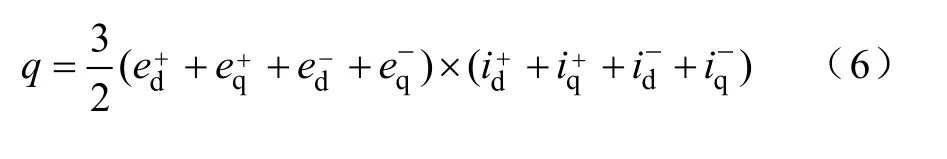
化简式(5)、式(6),得

式中,p0、q0分别为有功、无功功率的平均值;p1、p2分别为有功功率的2次余弦、正弦谐波峰值;q1、q2分别为无功功率的2次余弦、正弦谐波峰值。其具体表达式为
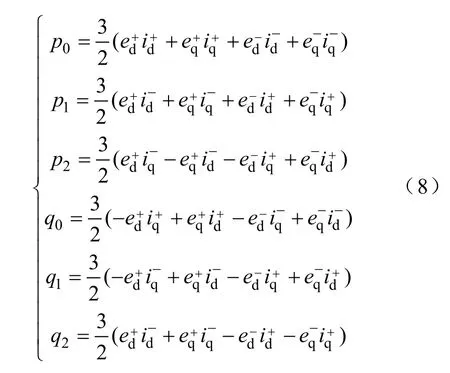
按照电网电压定向的原则,可知

结合式(9),式(8)可化简为

通过以上分析可知,当电网电压不平衡时,若只考虑基波分量,则会出现2次谐波功率。
2 电网电压不对称时的正负序分离方法
2.1 算法原理
三相电网电压由三相静止到两相静止坐标变换为
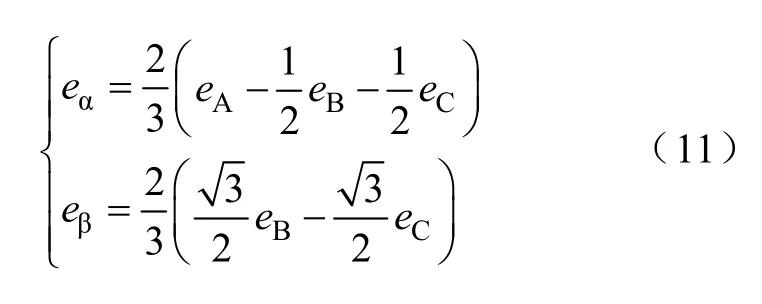
电网电压不对称时,αβ坐标系下的电网电压瞬时值可表示为

对式(12)等式两边进行微分
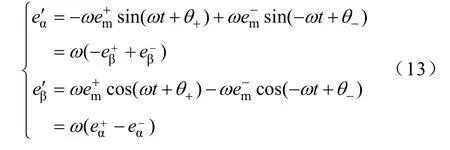
结合式(12)、式(13)可解得正、负序分量为
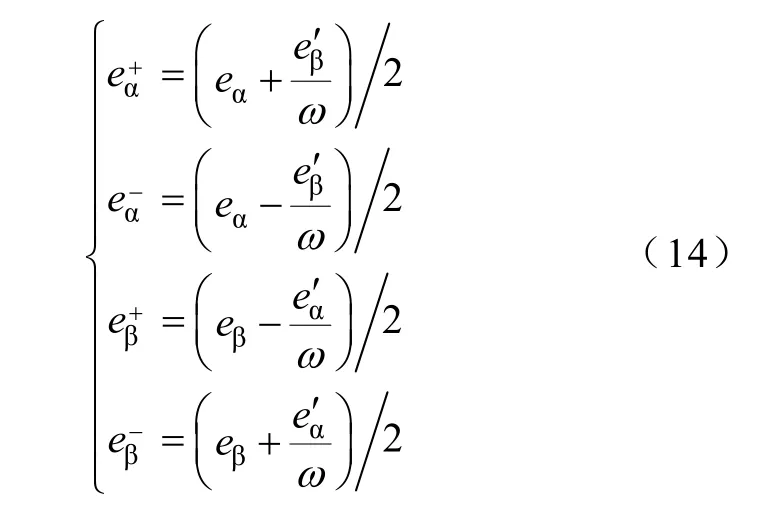
电压正、负序相角的正余弦值为

在dq坐标系下正、负序电网电压为

由以上分析可知,通过获取当前的电网电压瞬时值以及其对应的微分值,便可以分离出电压正、负序量,并获得正、负序相角的正余弦值。
2.2 利用交流遗忘积分算法对分离信号滤波
在分离正、负序分量时,采用了微分计算,容易受到采样误差的影响。为了消除这种影响,使用了交流遗忘积分算法。
当电网不对称时,电网电压的矢量轨迹为椭圆。当分离出正负序分量后,那么正序电压的矢量轨迹为正序圆,负序电压的矢量轨迹为负序圆。以正序为例介绍此方法。正序电压的矢量轨迹如图3所示。
第n次采样分离出的正序电压经前进一个角度后可以得到第n+1次的正序电压,变换关系为


图3 正序电压的遗忘算法示意图Fig.3 Diagram of forgetting algorithm of positive sequence voltage
式中,ΔT是采样周期。因此利用第n次电压估算出第n+1次电压,并用下式进行迭代修正

遗忘因子kf越小,系统的跟踪能力越强,动态过程中能够很快地跟踪电网电压的突变,但同时对采样噪声越敏感,滤波效果较差;遗忘因子kf越大,系统跟踪的能力减弱,但对采样噪声较不敏感,滤波效果越好。选取遗忘因子时,应该综合考虑。负序电压的处理与正序电压类似。

图4 正、负序电压滤波前与滤波后的比较Fig.4 Comparison of unfiltered and filtered
图4给出了电网电压正、负序分离的结果,滤波前的电网电压已经包含一定的正、负序信息,但由于采样信号噪声的存在,使得信号具有较大的随机性,采用交流遗忘积分后,可以获得平滑的电网电压的正、负序分量。
3 控制系统设计
3.1 外环设计
为了得到三相对称电流,需抑制负序电流,则负序电流的给定值应满足

将式(21)代入式(10)中,还需两个功率方程可解算出正序电流,得

以抑制负序电流为控制目标,必然带来有功功率和无功功率的波动,可得到其功率波动峰值为

平均有功功率给定与直流侧电压平均值有关,当外环采用 PI调节器时,调节器输出与直流电流相对应,因此平均有功功率给定可表示为
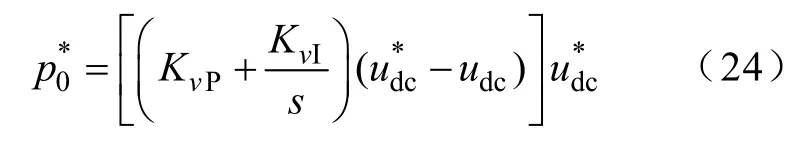
式中,KvP、KvI为电压调节器比例、积分增益。为了保证系统的稳定性,外环按照典型Ⅱ型系统设计,具体设计过程可参考文献[13]。
为了获得单位功率因数并网,一般令

由有功、无功功率给定,经式(22)可计算出正序电流给定值。
3.2 内环设计
电流内环调节器采用PI调节器,根据电流前馈解耦的控制规律。三相逆变器正、负序电流内环前馈解耦控制算法为

式中,KiP、KiI为电流调节器比例、积分增益。为了保证电流的响应速度,电流内环按照典型Ⅰ型系统设计,具体设计过程可参考文献[13]。
综上所述,并加入电网电压前馈控制,得到控制系统结构如图5所示。系统首先采集三相电网电压和电流,将电压、电流进行正、负序分离,并计算出正、负序相角的正余弦值;然后经坐标变换得到dq坐标系下正、负序电压与电流的分量。有功功率参考值通过式(24)获得;最后通过4个电流内环PI调节器式(26)、式(27)输出逆变器的参考输出电压,并经合成、限幅和调制后输出。

图5 控制系统结构Fig.5 Control system architecture
4 实验验证
在实验室搭建了1.5kW电压型并网逆变器实验样机,如图6所示。实验参数见下表。

图6 硬件平台图Fig.6 Figure hardware platform

表 实验样机参数Tab. Experimental parameters
主控芯片是DSP 56F8345。其中电压、电流量可由恒河WT 3000功率分析仪获得,其默认上下对称点为零点。有功功率和无功功率通过安捷伦DSOX 3014A示波器获得,因为本文关心的是功率波动的大小,所以测量时选择的是耦合交流。采用 3台调压器获得不对称ABC电网电压。完成了C相电压跌落40%下的传统双闭环控制策略并网实验,以及所提出的控制策略在三相电网电压对称时、C相电压跌落10%和C相电压跌落40%时的并网实验。
图7所示为在C相电网电压跌落40%时传统控制策略下的电流波形,可以看出电流出现了较大的畸变。图8a所示为在电网电压对称下的并网电流,电流峰值约为5A。从实验结果看,输出电流与电网电压同频同相,且三相电流对称,验证了该算法在电网对称的情况下是可行的。图8d说明在电网对称下有功功率和无功功率基本无波动。图 8b为 C相电网电压跌落 10%时的并网电流,电流峰值约为5.1A。从实验结果看,三相输出电流对称,验证了该算法在电网轻度不对称下的可行性。图 8e说明在电网轻度不对称时有功功率和无功功率波动较小。图8c为C相电网电压跌落40%时的并网电流,电流峰值约为5.8A。从实验结果看,三相输出电流对称,验证了该算法在电网重度不对称下是可行的。图 8f说明在电网重度不对称时有功功率和无功功率波动较大。

图7 C相电网电压跌落40%下的传统控制策略下电流波形Fig.7 The current waveform of traditional control strategy under C-phase grid voltage drop 40%


图8 C相电网电压在不同跌落时的并网电流和有功、无功功率Fig.8 Net current and active power, reactive power under C-phase grid voltage in a different drop
5 结论
本文首先对电网电压不对称条件下的并网型逆变器的数学模型和功率模型进行了描述,提出了瞬时正、负序分离方法,并进行了实验验证。在此分离方法基础上进行了电网对称、轻度不对称和重度不对称下的并网实验,实验结果表明了控制策略的有效性。与传统的双闭环控制策略相比,三相并网电流对称,且谐波较小。
[1] Rioual P, Pouliquen H, Louis J P. Regulation of a PWM rectifier in the unbalanced network state using a generalized model[J]. IEEE Transactions on Power Electron, 1996, 11(3): 495-502.
[2] N Enjeti P, Choudhury S A. A new control strategy to improve theperformance of a PWM AC to DC converter under unbalanced operating conditions[J]. IEEE Transactions on Power Electronics, 1993, 8(4): 493-500.
[3] Wang Yaw-Juen, Pierrat L. Probabilistic modelling of current harmonics produced by an AC-DC converter under voltage unbalance[J]. IEEE Transactions on Power Delivery, 1993, 8(4): 2060-2066.
[4] 胡家兵, 贺益康, 郭晓明, 等. 不平衡电网电压条件下双馈异步风力发电机系统的建模与控制[J]. 电力系统自动化, 2007, 31(14) : 47-56.
Hu Jiabing, He Yikang, Guo Xiaoming, et al. Modeling and control of the DFIG based wind-power generation system under unbalanced grid voltage conditions[J].Automation of Electric Power Systems, 2007, 31(14):47-56.
[5] Yin B, Oruganti R, Panda S K, et al. An output-powercontrol strategy for a three-phase PWM rectifier under unbalanced supply conditions[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 2140-2151.
[6] 何鸣明, 贺益康, 潘再平. 不对称电网故障下PWM整流器的控制[J]. 电力系统及其自动化学报, 2007,19(4): 13-17.
He Mingming, He Yikang, Pan Zaiping. Control of PWM rectifier under unbalanced input voltages[J].Proceedings of the CSU-EPSA, 2007, 19(4): 13-17.
[7] 章玮, 王宏胜, 任远, 等. 不对称电网电压条件下三相并网型逆变器的控制[J]. 电工技术学报, 2010,25(12): 103-110.
Zhang Wei, Wang Hongsheng, Ren Yuan, et al. Investigation on control of three-phase grid-connected inverters under unbalanced grid voltage conditions[J].Transactions of China Electrotechnical Society, 2010,25(12): 103-110.
[8] Li Zixin, Wang Ping, Li Yaohua, et al. Instantaneous power based control of three-phase PWM rectifier under distorted source voltages[C]. IEEE International Symposium on Industrial Electronics, Korea: Seoul,2009: 1234-1239.
[9] Roiu D, Bojoi R, Limongi L R, et al. New stationary frame control scheme for three phase PWM rectifiers under unbalanced voltage dips conditions[C]. IEEE Industry Applications Society Annual Meeting, Italy:Torino, 2008: 1-7.
[10] Li Zixin, Wang Ping, Li Yaohua, et al. Control of three-phase PWM rectifier under unbalanced input voltage conditions without sequential component extraction[C]. 14th International Power Electronics and Motion Control Conference(EPE-PEMC), 2010:179-184.
[11] 张兴, 季建强, 张崇巍, 等. 基于内模控制的三相电压型 PWM 整流器不平衡控制策略研究[J]. 中国电机工程学报, 2005, 25(13): 51-56.
Zhang Xing, Ji Jianqiang, Zhang Chongwei, et al.Study of internal model control based three-phase PWM rectifier under unbalanced input voltage condition[J]. Proceedings of the CSEE, 2005, 25(13): 51-56.
[12] 王久和, 杨秀媛. 电网不平衡时电压型PWM整流器控制策略[J]. 中国电机工程学报, 2011, 31(18): 14-20.
Wang Jiuhe, Yang Xiuyuan. Control strategy of voltage source PWM rectifiers under unbalanced voltage conditions[J]. Proceedings of the CSEE, 2011, 31(18):14-20.
[13] 张兴, 张崇巍. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2007.

