基于分裂电容法的LCL并网逆变器控制策略分析与改进

庄 超 叶永强 赵强松 王建宏 张 浩

（南京航空航天大学自动化学院 南京 210016）

0 引言

随着能源危机的加剧和智能电网的发展，有关新能源的分布式发电日益受到重视[1]。输出滤波器作为连接发电设备与电网的桥梁，近年来受到了广泛的关注和研究。就并网逆变器的输出滤波而言，LCL滤波器由于加入了电容支路，能用较小的电感更好地抑制开关频率附近的高次谐波，具有成本和功率密度低的双重优势[2]。

忽略寄生参数的影响，LCL滤波器可近似为一个无阻尼的三阶系统；在LCL的谐振频率处，其幅频特性曲线上存在一个增益为无穷大的谐振尖峰，该尖峰会放大谐振频率附近的干扰，显著地影响系统的闭环控制特性。尽管实际LCL滤波器元件的等效串联电阻（Equivalent Series Resistance, ESR）使得谐振尖峰有所减小，但这样的阻尼效果很弱。另外 LCL滤波器的相频特性在谐振频率处由-90°突变到-270°。为保证一定的相位裕度，截止频率必须设置在谐振频率之前，通常是 1/4～1/2[3]。采用常规PI控制时，受限于截止频率的设置，易使系统的低频开环增益不足，难以实现较小的稳态误差和抗扰动能力；而采用比例谐振（Proportional-Resonant，PR）需要设置多个谐振补偿环节且多个谐振补偿环节的权重设计也较复杂。

因此许多文献针对这一问题进行了分析并提出了改善 LCL滤波器控制特性的方法。文献[4]通过引入无源阻尼的方法达到抑制谐振尖峰的目的，简单方便但会使滤波性能变差，且不能解决系统截止频率过低的问题。文献[5-7]多引入了一个系统变量作为内环反馈，能够有效地抑制谐振尖峰而不影响滤波器本身的滤波效果，但需要增加一个电流传感器和复杂的内外环参数设计。文献[8]引入了电容电流的估算方法来实现有源阻尼，从而节省了一个电流传感器，但其估算效果取决于算法的鲁棒性和模型参数的准确性。不同于上述的网侧电流反馈，文献[9]采用逆变侧电流反馈，通过调节控制系统的数字延时提升了系统的稳定性，但由于是间接电流控制，受到电网电压谐波扰动的影响较大。因此文献[10]提出了适用于逆变侧电流反馈的电网电压前馈策略。文献[14]首次提出分裂电容法来控制LCL并网逆变器，通过零极点对消的方法将三阶系统降为一阶系统，可将控制对象等效为L型滤波器，大大提高了系统开环低频增益和相位裕度。

本文阐述了分裂电容法的谐振电流问题，分析了其谐振产生的理论模型，提出并验证了在两条电容支路上分别串入成比例阻尼电阻的方案，能在保持分裂电容降阶特性不变的基础上，显著地抑制谐振电流。并在此基础上，推导了适用于分裂电容法的电网电压前馈策略来抑制电网电压背景谐波的影响，并分析了前馈策略在实际应用中的有关问题。最后通过Matlab/Simulink软件仿真与一台2kW并网逆变器的实验，验证了理论分析的正确性与所提出控制策略的有效性。

1 LCL并网逆变器的控制策略比较

单相并网逆变器的结构如图1所示，L1与r1是逆变侧电感及其等效串联电阻，L2与r2是网侧电感及其等效串联电阻，Lg是电网电感。为表述方便，下文中L2包括网侧电感和电网电感两部分。

图1 单电流反馈的并网逆变电源系统Fig.1 Signal current feedback control methods for grid-connected inverter

对于逆变侧或网侧电流反馈控制而言，网侧和逆变侧的等效电阻对系统的频率特性影响很小，可以忽略，且这样的三阶系统处于无阻尼或欠阻尼状态。在数字控制中，采样和 PWM延迟通常近似为1.5拍的采样周期，在一定条件下会给系统带来额外的阻尼效果，延迟对系统稳定性的影响取决于采样频率和采样方式[12,13]。

由于上述两种控制对象均为三阶系统，所以只能在系统稳定性与稳态性能之间作折中选择。文献[11]所提出的分裂电容法可以很好地解决这个问题，如图2所示。

图2 分裂电容法电容中间电流反馈控制系统Fig.2 Current control methods by splitting the capacitor of LCL filter

该方法将原有的一条电容支路变为两条支路，采样两条支路间电流i12作为反馈。为方便表达，定义L=L1+L2，L1=αL，L2=(1-α)L，C=C1+C2，C1=βC，C2=(1-β)C。忽略电感的ESR时，被控对象的传递函数可简化为

当电容容量满足

将式（2）代入式（1）可得

由图3可见，当滤波元件按上述比例匹配时，降阶后的被控对象表现为一阶特性，可等效为L型滤波器，幅频特性为-20dB衰减，不存在谐振尖峰，相频特性始终为-90°。与逆变侧或网侧电流反馈相比，分裂电容法良好的频域特性大幅提高了系统的截止频率和带宽。针对控制设计的三个主要指标:截止频率fc、相位裕度PM和基频增益Tf0，给出了针对单电流反馈的 PI控制参数设计公式，其中Gi1_ui、Gi12_ui和Gi2_ui分别表示逆变侧电压到逆变侧电流反馈、分裂电容中间电流反馈和网侧电流反馈的传递函数。下式中Gim表示上述三种单电流反馈的被控对象传递函数[5]。

图3 不同电流反馈方式的被控对象传函伯德图a—网侧电流反馈 b—逆变侧电流反馈 c—分裂电容法Fig.3 Bode diagram of controlled object with different current feedback

本文实例中参数:L1=3mH，L2=2.6mH，C=11.2μF (C1=5.2 μF，C2=6 μF)，r=3.7Ω，Kpwm=1。按照式（4），PI参数设计结果见表1。

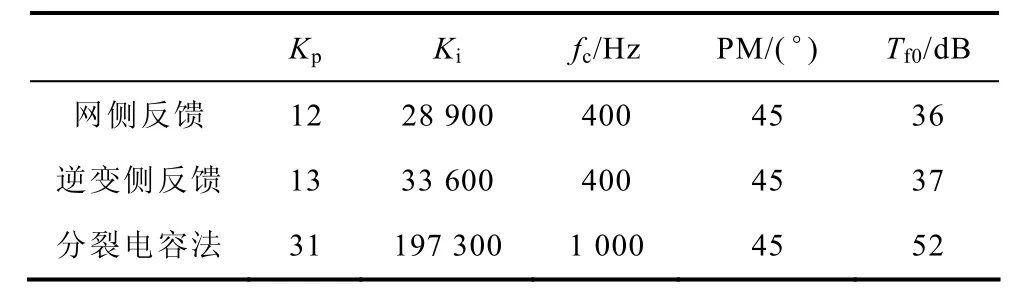
表1 不同电流反馈下PI参数与性能指标示例Tab.1 The example of PI controller parameter design and performance index with different current feedback

根据上表可见，由于避免了LCL滤波器谐振问题，分裂电容法通过选取较大的截止频率，取得较高的基频增益，从而提高稳态准确度和抗扰动能力，且不需要额外的阻尼。但这也引入了其他的问题，将在下面作详细讨论。另外电感L1、L2的等效串联电阻r1、r2的影响在文献[14]中已作讨论。

2 传统分裂电容法的分析与改进

2.1 分裂电容法存在的谐振问题

式（1）中对消掉的公因式为

将式（6）代入式（5），可得

在谐振频率处，式（1）的零极点不能合理对消，因此研究分裂电容法在谐振频率处的电路关系是必要的。

LCL滤波器作为一种二端口网络，激励源包括逆变电压源uinv(ω)和电网电压源ug(ω)两部分。逆变电压中谐振频率分量uinv(ωr)主要由调制信号和死区效应两部分组成，其中调制信号中的谐振频率分量主要来自于电网电压前馈，另外由于实际中滤波元件可能不完全成比例，电流反馈中也会引入少量谐振频率分量。电网电压中谐振频率处的分量ug(ωr)主要由其他并网设备谐振频率处电流谐波和与其各自对应输出阻抗导致[15]。

为简化过程，首先分析逆变电压在谐振频率处分量uinv(ωr)激励下的电路响应，因此电网电压源可作短路等效。这样分裂电容法在谐振频率处的滤波器等效电路如图4所示。

图4 LCL滤波器谐振频率处等效电路Fig.4 The equivalent circuit of LCL filter at resonant frequency

由式（6）得

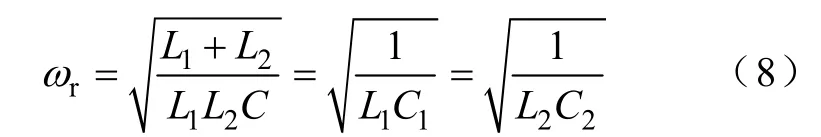
定义逆变侧电感L1与电容C1的串联阻抗为Z1(ω)，网侧电感L2与电容C2的并联阻抗为Z2(ω)，则有

式（10）表明在谐振频率处网侧电感与网侧电容并联阻抗为无穷大，因此反馈电流i12(ωr)为零。而逆变侧电感与逆变侧电容由电压源uinv(ωr)的激励发生谐振。另外网侧电感与网侧电容由电容C1上的电压uC1(ωr)激励，矢量图如图5所示。

图5 网侧谐振环路的矢量图Fig.5 The vector diagram of grid side resonant loop

由此得

假设电网电压中存在谐振频率处的分量，同样会存在类似的谐振环路。那么实际入网电流中的谐振分量可以表达为

式中，Gi2_ui为逆变电压到入网电流传函，Gi2_ug为电网电压到入网电流传函。

综上所述，通过滤波元件合理配比，分裂电容法将原有的LCL滤波器分成两个独立的谐振环路，那么两个谐振环路之间的电流作为反馈时就不包含谐振频率处的信号，但谐振电流仍然存在于谐振环路内，降低了入网电流的波形质量。

上述分析忽略了滤波元件的ESR，实际中只要滤波元件的ESR在合理的范围内，谐振电流会明显地影响入网电流的总谐波畸变，给分裂电容法的实际应用带来障碍。需要指出的是，文献[11]中的加权电流控制（Weighted-Average Control，WAC）也存在类似的问题。

2.2 加入无源阻尼的分裂电容法

由于分裂电容法的谐振问题与其他电流反馈方式的谐振问题本质上是相同的，都是由于LCL滤波器是一个三阶无阻尼系统，使得逆变侧电压或电网电压到入网电流的传函存在谐振尖峰。所以可根据以往文献中加入阻尼的方式来抑制谐振电流，有无源阻尼和有源阻尼两种途径。采用有源阻尼需要两个电流传感器和复杂的控制设计，因此本文仅讨论加入无源阻尼的方法，如图 6所示。文献[16]中讨论了6种无源阻尼的谐振抑制效果、对滤波器高频谐波衰减能力的影响和阻尼电阻的额外损耗。综合考虑后选用滤波电容串联电阻的方案。

图6 加入无源阻尼的分裂电容法LCL滤波器等效电路Fig.6 The equivalent circuit of LCL filter for split-capacitor method with passive damping

图 6 中，定义r=r1+r2，r1=γr，r2=(1-γ)r，仍将电容支路间的电流i12作为反馈，那么逆变输出电压uinv到反馈量i12的传递函数为

当滤波元件值满足

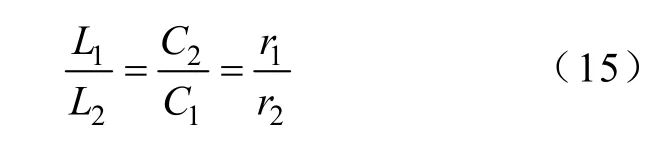
即α=1-β=γ，将式（15）代入式（14），Gi12_ui仍可简化为一阶系统，即

受逆变输出电压和电网电压中谐振频率处分量的影响，网侧电感谐振电流同样可表示为式（13）。

在满足式（15）的基础上，计算两条电容支路的并联阻抗得

电容支路等效如图7所示，可见串入阻尼电阻后，等效总电容量保持不变，等效总电阻rd仅为αβr，其中α＜1，β＜1。由此可见串入阻尼的分裂电容法和常见的无源阻尼对滤波器电路特性的影响是相同的，不影响滤波器的谐振频率，那么可以参照网侧电流反馈无源阻尼的阻值设计。另外由于分裂电容法串入的阻尼只是为了抑制谐振，不影响系统稳定性，则阻尼电阻值小且设计相对简单。

图7 加入无源阻尼的分裂电容法等效电容支路Fig.7 The equivalent capacitor branch of split-capacitor method with passive damping

2.3 电网线路电感对分裂电容法的影响

由于电网电感的存在，使得网侧总电感L2具有不确定性，这使得式（14）的零极点不能完全对消，那么被控对象就不是理想的一阶特性。图8所示为电网电感变化时系统的开环传函伯德图。

图8 电网电感变化时系统的开环传函伯德图Fig.8 The Bode diagram of controlled object with grid inductance varied

由图 8可见，当网侧总电感L2由 2.6mH变化到5mH时，电网阻抗的存在使得中低频处的系统开环增益降低，导致系统的截止频率减小，对应的相位裕度也随之降低，但整体而言系统总能保持稳定且具有较好的稳定裕度。

在未加入电网电压前馈的并网系统中，逆变器与网侧的谐波交互与其输出导纳密切相关[15]，而电网线路电感就是影响逆变器输出导纳的主要因素之一。采用改进后的分裂电容法，电网电压ug到入网电流i2的传函Gi2_ug(s)为

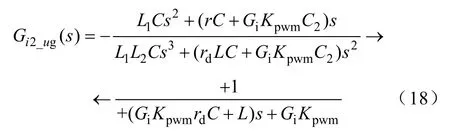
图9所示为采用PI控制电流调节器，网侧总电感L2在2.6mH～5mH内变化时Gi2_ug(s)的伯德图。可见随着网侧电感增大，对高频谐波的抑制能力逐渐增强，但对中低频电网谐波的抑制能力基本没有影响。由于PI控制器在中低频处的增益有限，在未加入电压前馈时，对电网畸变的抑制不能取得满意的效果。

图9 电网电感变化时并网逆变器输出导纳幅频特性Fig.9 The amplitude-frequency characteristic of grid connected inverter output admittance with varying grid inductance

3 适用于分裂电容法的电压前馈策略

电网电压前馈技术能有效地抑制入网电流中由电网电压背景谐波引入的低频谐波污染。关于LCL滤波器的低频电网电压谐波抑制的问题，已有文献[7, 17, 18]分别就基于逆变侧电流反馈、有源阻尼与状态反馈控制等3种电流控制方法的电网电压前馈进行了研究，并取得了良好的效果。下面将重点研究用于分裂电容法的电网电压前馈策略。

图10所示为拟加入前馈的控制框图，为消除电网电压对系统输出的影响，根据已有的前馈设计方法[19]，即在iref=0时，有i2=0，只需要使uC=ug成立即可。因此去掉图10中的虚线部分不影响求取前馈传递函数GFF。简化后的控制框图如图11所示。

图10 加入前馈的基于分裂电容法的并网逆变器控制框图Fig.10 The control block diagram of grid connected inverter based on split capacitor method with grid voltage feed-forward

图11 用于电压前馈推导的简化控制框图Fig.11 The simplified control block diagram for derivation of voltage feed-forward strategy

为保证上述条件，只需使ug到uc的传递函数等于 1。令(GFF)-1=uc(s)/uFF(s)，直接求出传函(GFF)-1后，即可得到GFF。按上述方法，可得到

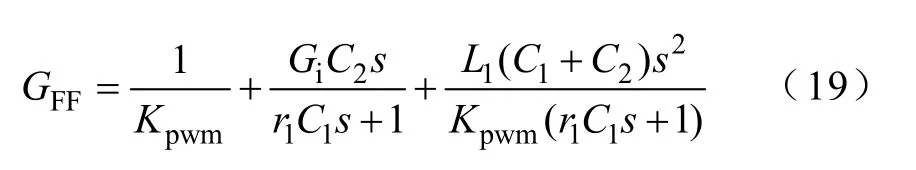
由于前馈传函GFF中的第二项包含电流调节器，可将这一项加在电流调节器之前以实现参数解耦。加入电网电压前馈后的控制框图如图12所示。其中

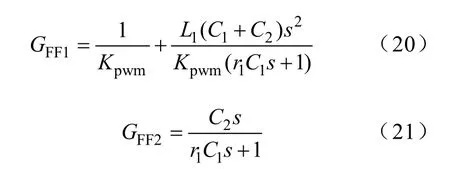
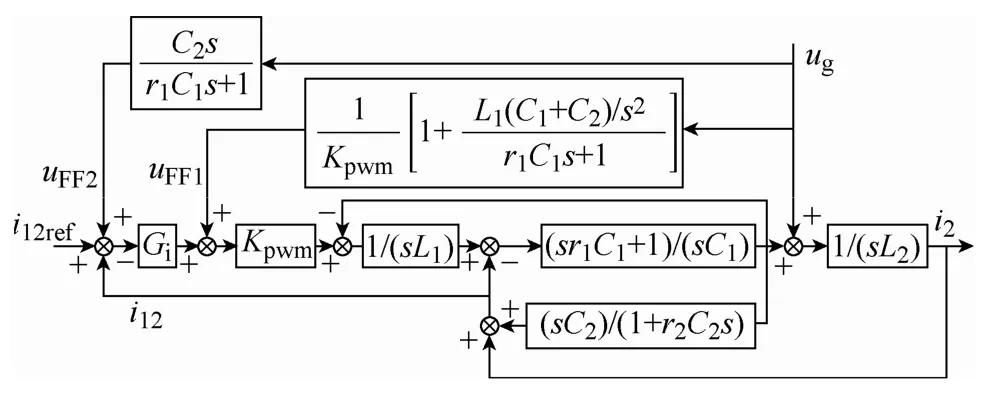
图12 解耦后的电网电压前馈的控制框图Fig.12 The control block diagram with the decoupled voltage feed-forward strategy

当阻尼电阻值取零时，所推导的前馈策略也可用于传统的分裂电容法。

由于数字控制系统中存在计算和 PWM延迟，实际中的调制与逆变环节不能单纯由Kpwm来等效，下面讨论在不同拍数延迟下电压前馈的补偿效果。图13是按照上述补偿策略在不同延迟拍时电网电压ug到入网电流i2传递函数的伯德图。在中低频段，可用不同时间常数的惯性环节来近似不同拍数的延迟环节，即

式中，Ts为采样周期。

图13 存在控制延迟时并网逆变器输出导纳的幅频特性a—无前馈时 b—有前馈，0.5拍延迟c—有前馈，1.5拍延迟 d—有前馈，2.5拍延迟Fig.13 The amplitude-frequency characteristic of grid connected inverter output admittance with control delay

作为一种前馈控制策略，其本身并不影响闭环系统的稳定性，但采样、计算与 PWM的延迟会影响前馈控制的效果。由图13可以看到，在延迟存在时，该前馈方案也能够提高对中低频段电压谐波的抑制能力，但随着延迟的拍数增大，抑制效果会逐渐变差。因此实际中采用尽量少的延迟拍数有利于实现前馈控制的作用。

4 仿真与实验验证

为了验证上述理论分析与所提出方法的可行性，本文对一台2kW的单相并网逆变器进行了仿真与实验。具体参数如下:直流母线电压Ed=370V，电网电压Vg=220V，开关频率fsw=10kHz, 母线电容Cdc=2 000μF，逆变侧电感L1=3mH，网侧电感L2=2.6mH，逆变侧电容及串联电阻C1=5.2μF，r1=8.4Ω，网侧电容及串联电阻C2=6μF，r2=7.1Ω。滤波器谐振频率fr=1 270Hz。为了与实验背景保持一致，通过对实际电网电压进行傅里叶分析，得到35次以内各奇次谐波分量的幅值和相角，将各谐波分量分别用独立电压源表示，那么这些电压源之和便可用来模拟仿真实际电网电压波形。

经测量分析，本地电网电压总谐波畸变为4.1%。在 Matlab/Simulink仿真中功率部分仿真步长为0.4μs，控制部分仿真步长为0.1ms。由图14a可见，在未加入阻尼时，入网谐振电流较大，总谐波畸变（THD）为 4.88%；加入阻尼后，谐振电流得到明显抑制，总谐波畸变降为2.39%，如图14b所示。图14c为加入电网电压前馈后，入网电流波形受电网电压影响明显减小，总谐波畸变降到1.69%。

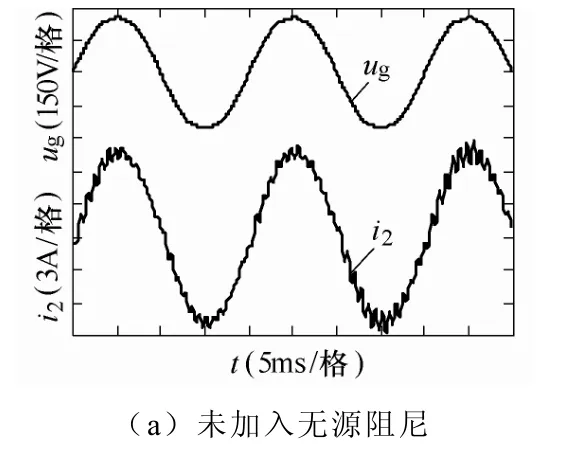
图14 对比仿真的电网电压、电流波形Fig.14 The simulated waveforms of grid voltage and current

由图15可见，在未加入电网电压前馈时，随着电网线路电感的增加，入网电流的THD逐渐减小，这主要是由于逆变器输出导纳减小导致。加入前馈后，入网电流的THD整体小于未加入前馈，且受电网电感变化影响不明显，具有较强的鲁棒性。

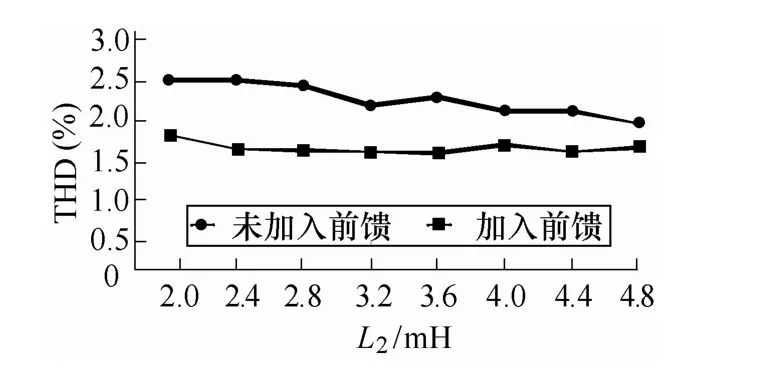
图15 电网电感对入网电流波形质量的影响Fig.15 The effect of grid inductance on waveform quality of grid current

与仿真参数相同，实验结果如图 16、图 17所示。为更好地抑制低频谐波的效果，实验中采用重复控制与 PI控制结合的复合控制结构来验证上述理论分析。由于实际中滤波电感呈非线性，为了在额定峰值电流区间内都能较好地实现降阶特性，应选用具有较好线性度的滤波电感。

图16 未加入电压前馈的入网电流实验波形及FFTFig.16 The experiment waveforms and FFT of gird current without voltage feed-forward strategy

表2是 IEEE Std.929—2000和 IEEE Std.P1547标准对并网发电系统注入电网的电流谐波标准。由图16的实验结果可见，未加入阻尼的分裂电容法的THD为3.34%，在入网电流中引入了明显的谐振电流，远超出了表2中0.6%的上限，不符合上述标准要求。加入相应的阻尼电阻后，THD降为2.42%，入网谐振电流得到了很好的抑制，完全符合上述要求。

表2 并网发电系统入网电流谐波含量限制Tab.2 Grid current harmonic content restrictions in grid-connected power system

上述电压前馈的离散化采用前向差分法。采样、计算和 PWM延迟估算为 1.5拍。在加入无源阻尼的分裂电容法基础上，应用式（19）的电压前馈策略后，如图 17所示，入网电流 THD进一步降至1.91%。

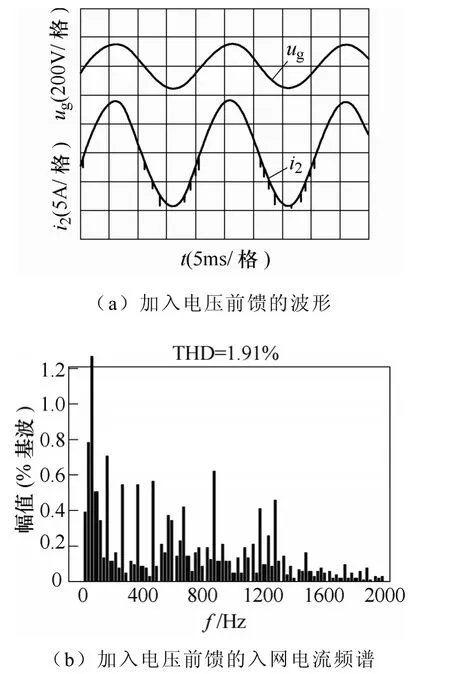
图17 加入电压前馈的入网电流实验波形及FFTFig.17 The experiment waveforms and FFT of gird current with voltage feed-forward strategy

5 结论

本文主要分析了分裂电容法导致谐振电流的理论模型。采用串入成比例电阻的无源阻尼法来抑制谐振电流并分析了电网电感变化对系统稳定性和输出导纳的影响。推导了基于分裂电容法的电压前馈策略，以改善电网电压谐波导致的入网电流畸变，并讨论了存在系统延迟下电压前馈策略的有效性。仿真和实验结果表明针对分裂电容法的分析是正确的，改进是有效可行的。但由于无源阻尼引入了额外损耗，使得该方法适用于小功率场合，在大功率场合可能由于损耗过大而不宜采用。针对这一点，后续工作将在分裂电容的基础上引入有源阻尼来避免额外损耗。

[1] Frede Blaabjerg, Remus Teodorescu, Marco Liserre,et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industry Electronics, 2006, 53(5):1398-1409.

[2] Kamarn Jalili, Steffen Bernet．Design of LCL filters of active-front-end two-level voltage-source converters[J]. IEEE Transactions on Industry Electronics, 2009,56(5): 1674-1689.

[3] Dannel J, Wessels C, Fuchs F．Limitations of voltageoriented PI current control of grid-connected PWM rectifiers with LCL filters[J]. IEEE Transactions on Industry Electronics, 2005, 52(5): 1281-1291.

[4] 郭小强, 邬伟杨, 顾和荣, 等. 并网逆变器 LCL接口直接输出电流控制建模及稳定性分析[J]. 电工技术学报, 2010, 25(3): 102-109.

Guo Xiaoqiang, Wu Weiyang, Gu Herong, et al. Modelling and stability analysis of direct output current control for LCL interfaced grid-connected inverters[J].Transactions of China Electrotechnical Society, 2010,25(3): 102-109.

[5] 鲍陈磊, 阮新波, 王学华, 等. 基于 PI调节器和电容电流反馈有源阻尼的 LCL型并网逆变器闭环参数设计[J]. 中国电机工程学报, 2012, 32(25):133-142.

Bao Chenlei, Ruan Xinbo, Wang Xuehua, et al. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping[J]. Proceedings of the CSEE, 2012, 32(25):133-142.

[6] 刘飞, 查晓明, 段善旭. 三相并网逆变器 LCL滤波器的参数设计与研究[J]. 电工技术学报, 2010,25(3): 110-116.

Liu Fei, Zha Xiaoming, Duan Shanxu. Design and research on parameter of LCL filter in three-phase grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 110-116.

[7] 伍小杰, 孙蔚, 戴鹏, 等. 一种虚拟电阻并联电容有源阻尼法[J]. 电工技术学报, 2010, 25(10): 122-128.

Wu Xiaojie, Sun Wei, Dai Peng, et al. An active damping method of virtual resistor in parallel with capacitor[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 122-128.

[8] 张学广, 刘义成, 王瑞, 等. 一种新型的PWM变换器LCL滤波器有源阻尼控制策略[J]. 电工技术学报,2011, 26(10): 188-192.

Zhang Xueguang, Liu Yicheng, Wang Rui, et al. A novel actice damping control strategy for PWM converter with LCL filter[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 188-192.

[9] 张强, 张崇巍, 张兴, 等. 风力发电用大功率并网逆变器研究[J]. 中国电机工程学报, 2007, 27(16):55-59.

Zhang Qiang, Zhang Chongwei, Zhang Xing, et al.Study on grid-connected[J]. Proceedings of the CSEE,2007, 27(16): 55-59.

[10] 吴云亚, 谢少军, 阚加荣, 等. 逆变器侧电流反馈的LCL并网逆变器电网电压前馈控制策略[J]. 中国电机工程学报, 2013, 33(6): 54-60.

Wu Yunya, Xie Shaojun, Kan Jiarong, et al. Grid voltage feed-forward control strategy with inverterside current feedback LCL grid-connected inverter[J].Proceedings of the CSEE, 2013, 33(6): 54-60.

[11] Shen Guoqiao, Zhu Xuancai, Zhang Jun, et al. A new feedback method for PR current control of LCL-filter-based grid-connected inverter[J]. IEEE Transaction on Industry Electronics, 2010, 57(6): 2033-2041.

[12] 李军, 李玉玲, 陈国柱. 无阻尼 LCL滤波器的并网变流器稳定性控制策略[J]. 电工技术学报, 2012,27(4): 110-116.

Li Jun, Li Yuling, Chen Guozhu. A stability control strategy for PWM converter with undamped LCL-filter[J]. Transactions of China Electrotechnical Society,2012, 27(4): 110-116.

[13] Yin Jinjun, Duan Shanxu, Liu Bangyin. Stability analysis of grid-connected inverter with LCL filter adopting a digital single-loop controller with inherent damping characteristic[J]. IEEE Transaction on Industry Electronics, 2009, 56(2): 380-388.

[14] 沈国桥, 徐德鸿. LCL滤波并网逆变器的分裂电容法电流控制[J]. 中国电机工程学报, 2008, 28(18):36-41.

Shen Guoqiao, Xu Dehong. Current control for grid-connected inverters by splitting the capacitor of LCL filter[J]. Proceedings of the CSEE, 2008, 28(18):36-41.

[15] 许德志, 汪飞, 毛华龙, 等. 多并网逆变器与电网的谐波交互建模与分析[J]. 中国电机工程学报,2013, 33(12): 64-71.

Xu Dezhi, Wang Fei, Mao Hualong, et al. Modeling and analysis of harmonic interaction between multiple grid-connected inverters and the utility grid[J]. Proceedings of the CSEE, 2013, 33(12): 64-71.

[16] Rafael Pena, Marco Liserre, Frede Blaabjerg, et al.Analysis of the passive damping losses in LCL-filterbased grid converters[J]. IEEE Transaction on Power Electronics, 2013, 28(6): 2642-2646.

[17] 王学华, 阮新波, 刘尚伟, 等. 抑制电网背景谐波影响的并网逆变器控制策略[J]. 中国电机工程学报,2013, 33(6): 54-60.

Wang Xuehua, Ruan Xinbo, Liu Shangwei, et al.Control strategy for grid-connected inverter to suppress current distortion effected by background harmonics in grid voltage[J]. Proceedings of the CSEE, 2013,33(6): 54-60.

[18] Xue Mingyu, Zhang Yu, Kang Yong, et al. Full feedforward of grid voltage for discrete state feedback controlled grid-connected inverter with LCL filter[J].IEEE Transaction on Power Electronics, 2012, 27(10):4234-4247.

[19] 胡寿松. 自动控制原理[M]. 北京: 科学出版社,2001.