基于电容电荷平衡的滞环控制策略

赵晋斌 戴剑丰 屈克庆

（上海电力学院电气工程学院 上海 200090）

0 引言

随着现代信息科学的快速发展，直流开关变换器正朝着集成化、高效率、轻量化和小型化的趋势发展，如何设计满足以上要求的直流开关变换器成为了电力电子领域面临的一大挑战，控制策略的研究是其中的热点之一。直流变换器最基本的控制方法是电压控制，电压控制是一种单环控制，其开环传递函数中存在较为复杂的极点，需要搭建复杂的补偿网络，这不仅增加了控制电路的设计难度，而且具有较差的动态负载性能[1,2,14]。针对以上问题，国内外学者开展了深入的研究[4-13]，其中电流模式控制方法[3,4]是在电压反馈的基础上引入电流反馈实现双环控制，通过调节电感电流实现对输出电压的控制，该方法需要复杂的斜坡补偿，且响应速度受制于电压环控制器；滑模变结构控制方法[5,6]是将受控非线性系统的状态轨迹引向预先指定的状态平均空间平面上，具有较好的稳定鲁棒性和动态特性，但存在设计复杂、调试要求高等问题；V2控制[7,8]采用输出电压纹波作为内环的检测量，对输入电压扰动具有较好的抑制能力，但抗干扰能力差，需采用谐波补偿。

为了进一步提高开关变换器的鲁棒性和瞬态响应速度，本文提出了一种基于电容电荷平衡的滞环控制策略。该策略无需误差放大器及其复杂的补偿网络，因此对负载突变和输入突变具有更快的响应速度，并具有良好的抗干扰能力。最后，以 Buck变换器为例，使用状态空间平均法对其进行小信号建模，讨论了控制参数对系统的影响，并通过频域、时域仿真和实验结果验证了该方法的优越性能。

1 控制原理分析

图1给出了本文提出的滞环控制Buck变换器。控制电路由滞环比较器U，电容C，电阻Rf和R组成。滞环比较器U的工作原理如图2所示。输出电压和VU则分别通过Rf和R支路反馈到电容C，利用反馈支路信号的变化对电容C进行充电和放电，从而调整电容C两端电压来达到调制的效果。另外，滞环比较器的输出端通过电阻R2与其同相输入端相连，再通过电阻R1连接到参考电压Vref，这样通过滞环比较器输出端电压的翻转来设置滞环高阈值电压VH和低阈值电压VL。

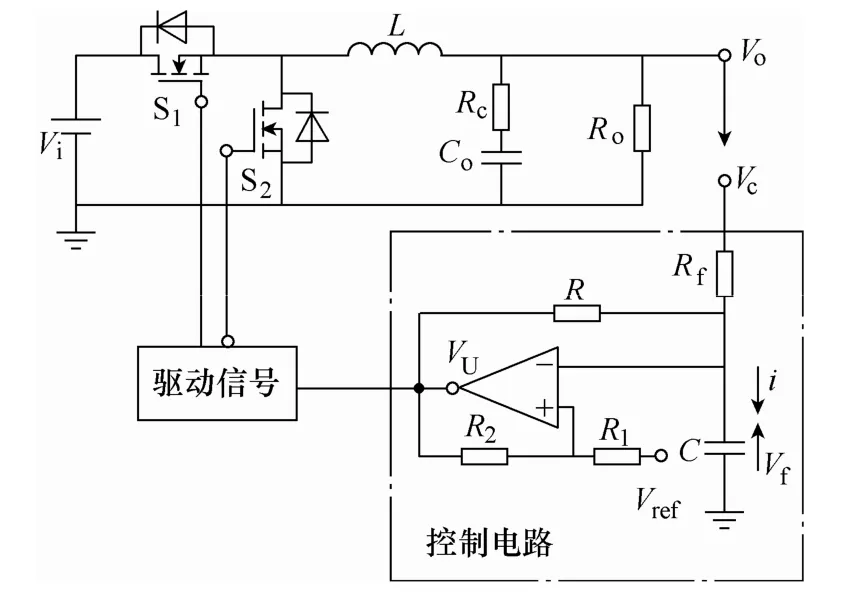
图1 提出的滞环控制Buck变换器Fig.1 Schematics of Buck converter with proposed hysteresis control

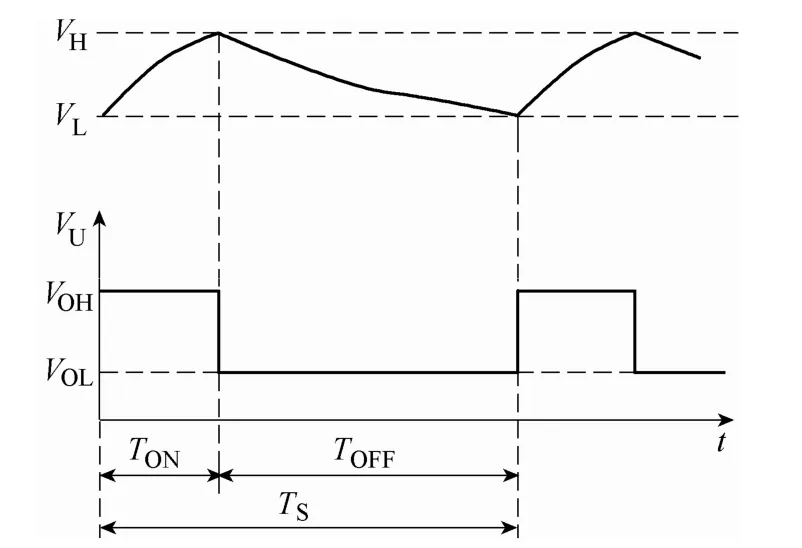
图2 滞环比较器的工作原理Fig.2 Control characteristics of hysteresis comparator

控制电路的工作原理如下:①S1导通时，当输出电压变大（小）时，电容C的充电电流将会增大（减小），这样开关S1的导通时间TON将变小（增大）；②S1关断时, 当输出电压变大（小）时，电容C的放电电流将减小（增大），这样开关S1关断时间TOFF变大（减小）。因此 Buck变换器的占空比可迅速调节使输出电压快速恢复到稳定状态。

2 小信号模型及动态分析

为了简化分析，所有电路器件均被认为工作在理想状态。Vf是电容两端电压，VH和VL是滞环比较器的高低阈值电压，VU是比较器的输出电压。假定开始时刻为t=0。其中高、低阈值电压VH、VL计算式为

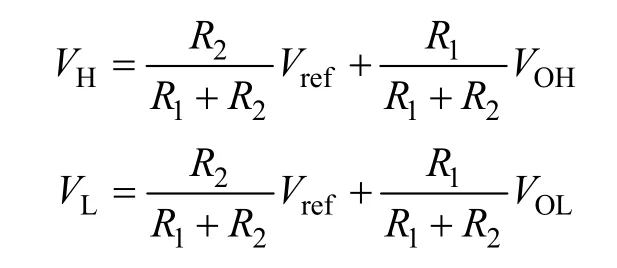
2.1 导通时刻（0＜t＜TON）

当滞环比较器输出信号VU是高电平时，通过电阻R和Rf所在的反馈支路对控制电路中的电容C进行充电，根据基尔霍夫电流定律有

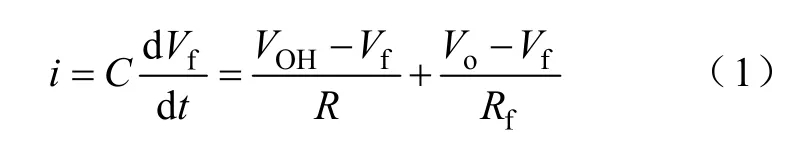
假设初始条件为Vf(0)=VL，可以得到

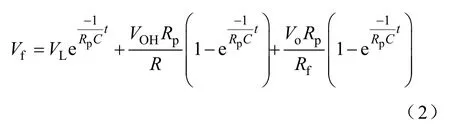
式中，Rp=RRf/(R+Rf)。

通过式（2）可知，Vf从VL以指数形式增加到。设定Vf=VH和t=TON，可近似得到

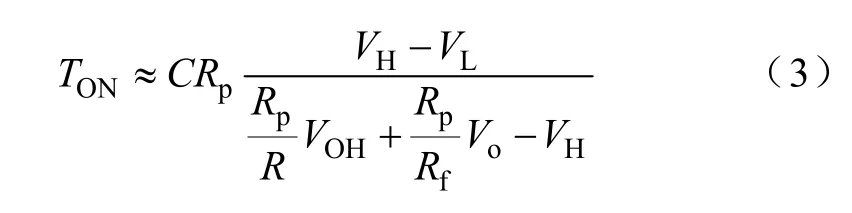
2.2 关断时刻（TON＜t＜TS）

当滞环比较器输出信号VU是低电平时，电容C通过电阻R和Rf所在的反馈支路进行放电，根据基尔霍夫电流定律，能够得到

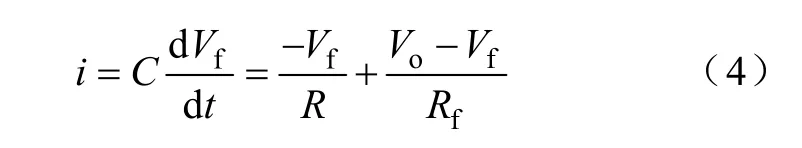
在Vf(TON)=VH时，能够得到

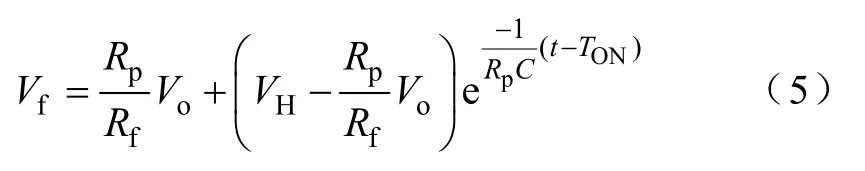
通过式（5）可知，Vf从VH以指数形式减小到。设定Vf=VL和t=TON+TOFF，可近似得到

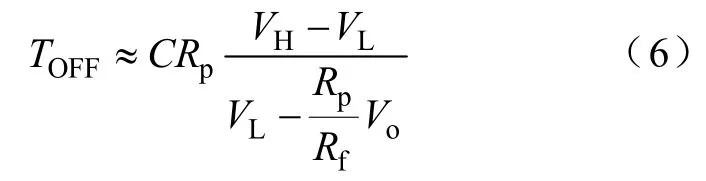
结合式（3）和式（6），并根据D=TON/ (TON+TOFF)可得

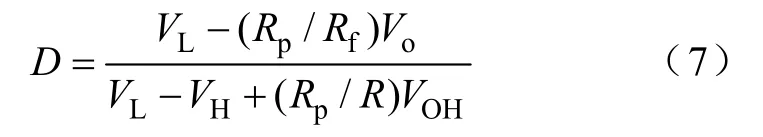
根据oi/DVV=和式（7），可以近似得到输出电压的表达式

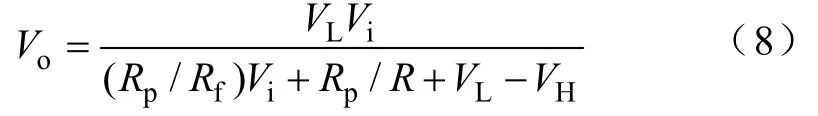
图 3为新型滞环控制 Buck变换器的小信号等效电路，图 4是 Buck变换器闭环模型框图。根据状态空间平均法[15]可以求得主电路各开环传递函数分别为

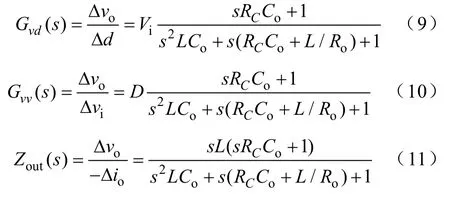
式中，k为输出电压反馈支路增益，RC为滤波电容的等效寄生电阻。

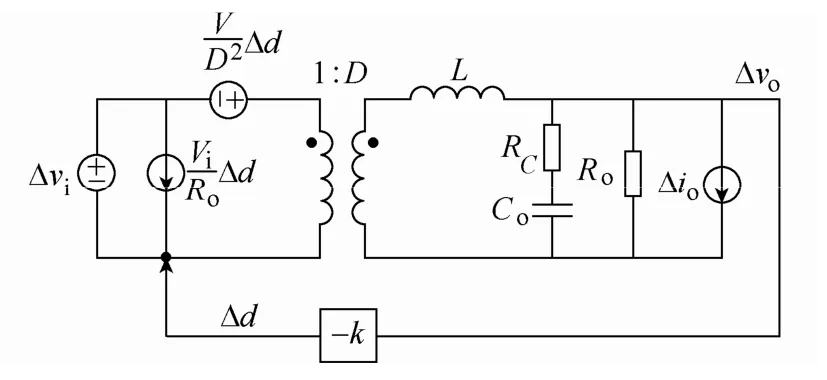
图3 提出滞环控制的Buck变换器小信号等效电路Fig.3 Small signal equivalent circuit of the Buck converter with proposed hysteresis control

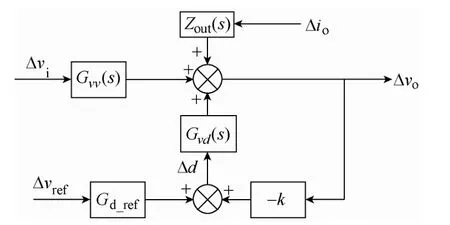
图4 提出滞环控制Buck变换器的模型框图Fig.4 Model diagram of the proposed hysteresis controlled Buck converter

不考虑Vref的扰动，式（7）的小信号扰动可表示为

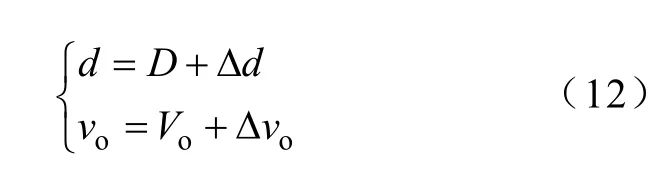
将式（12）代入式（7）可以得到

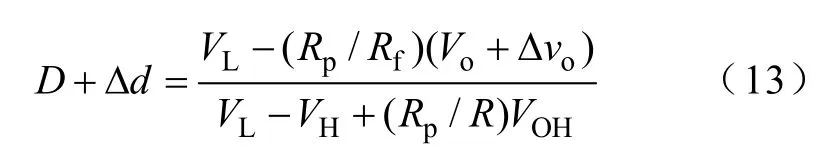
通过式（7）和式（13），可以得到输出电压反馈环路增益为

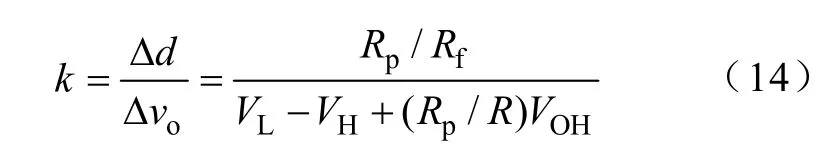
结合图4并利用梅森公式[16]可以求得其闭环传递函数分别如下。

“控制-输出”闭环传递函数为

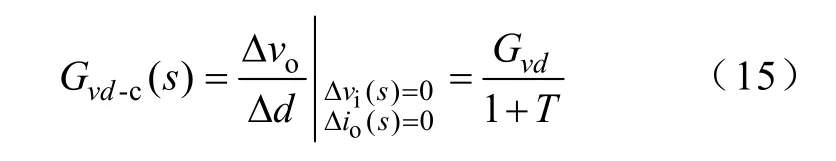
其中，环路增益T=kGvd，则式（15）可为

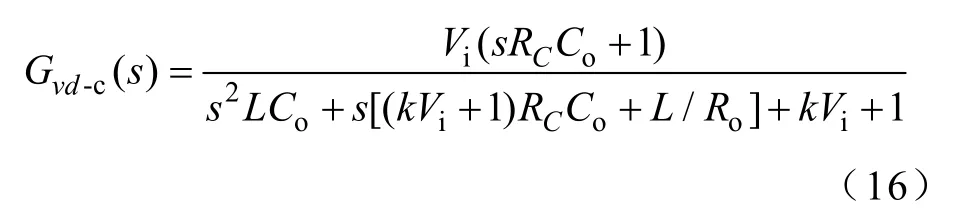
同理“输入-输出”闭环传递函数为

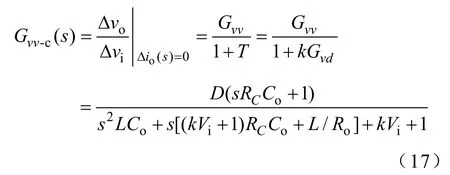
闭环输出阻抗out-cZ为

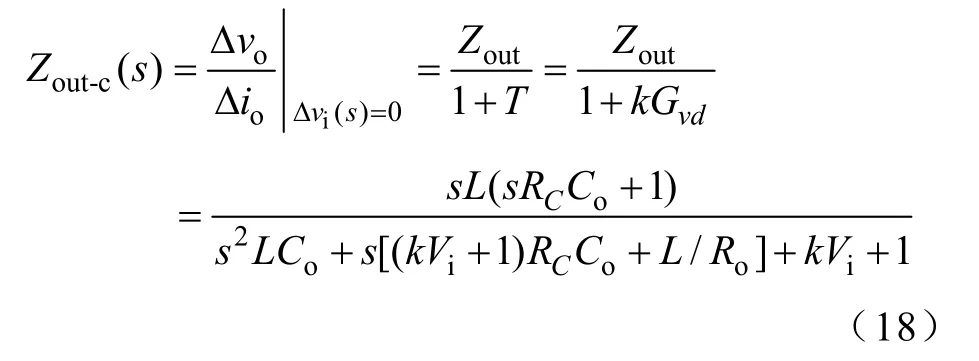
3 仿真和实验验证

3.1 频域仿真分析

首先，分析了反馈支路控制参数Rf对系统的影响，反馈电阻Rf作为控制器的关键参数，其取值直接影响着控制器性能的好坏。图5为不同反馈电阻Rf时的环路增益伯德图，从图中可以看出T(s) 在所有的频段内都会随着Rf的改变而变化，且随着Rf的减小，环路增益会增大，相位裕度也会增大，且具有较高的截止频率和高的带宽；图6为不同反馈电阻Rf时的闭环输入-输出伯德图，由图可知Rf越小，闭环输入-输出增益越小，抗输入扰动能力越好；图7则为不同反馈电阻Rf时的闭环输出阻抗伯德图，由图可知Rf越小，闭环输出阻抗越小，抗负载扰动能力越好。所以在保证系统稳定的范围内，较小的反馈电阻Rf会有更好的控制性能。综合选取的电路参数见下表。

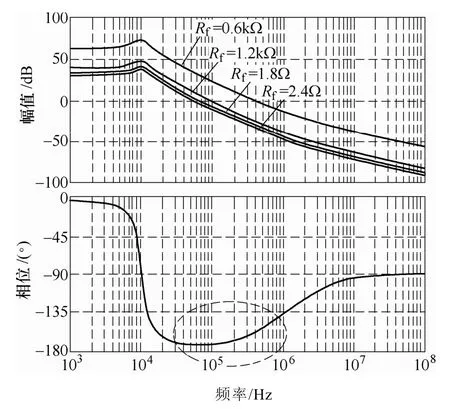
图5 不同电阻Rf时的环路增益伯德图Fig.5 Bode diagram of loop gain takingRf as a parameter

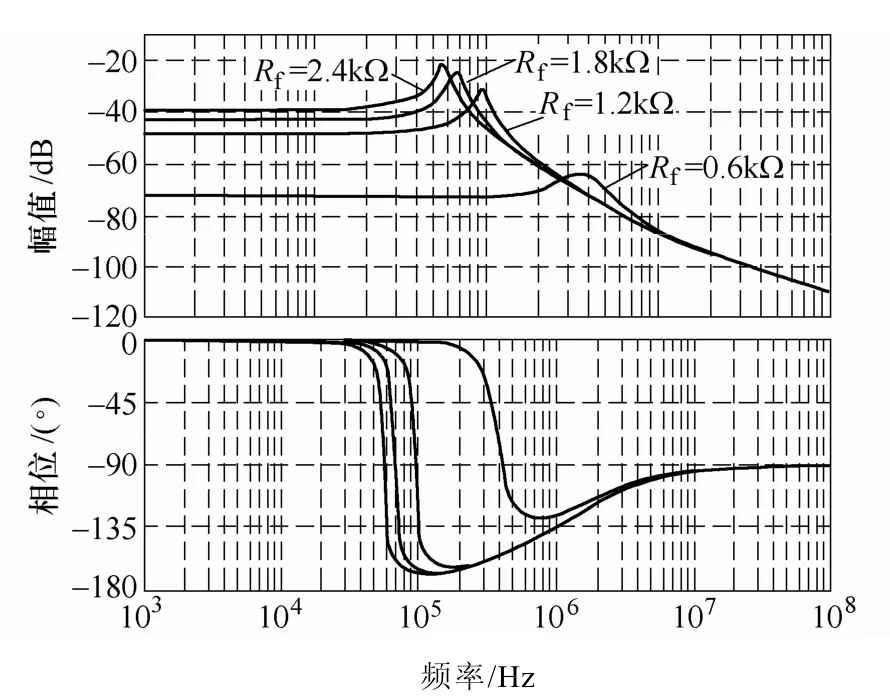
图6 不同电阻Rf时的闭环输入-输出伯德图Fig.6 Bode diagram of closed loop input-output taking Rfas a parameter

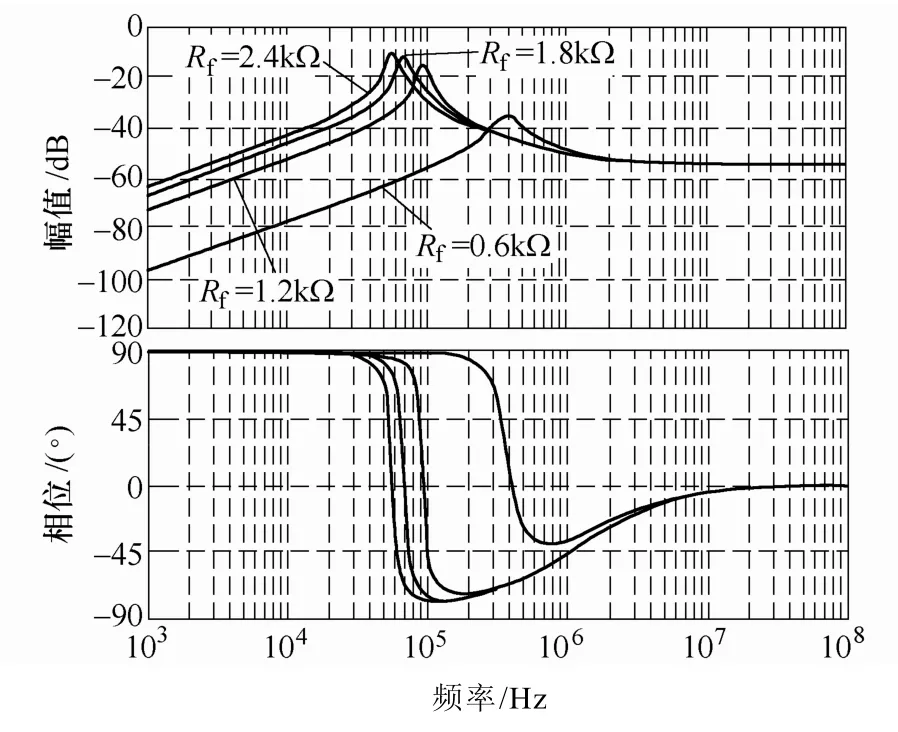
图7 不同电阻Rf时的闭环输出阻抗伯德图Fig.7 Bode diagram of closed loop output impedance takingRfas a parameter

表 电路参数Tab. The circuit parameters

图8a为环路增益传递函数的奈奎斯特曲线，图8b为在点（-1,i0）附近的放大区域图，从图中可以看出该曲线没有包围点（-1,i0）也没有穿越它，且图9可以看出开环传递函数的右半平面不存在极点数，则从奈奎斯特稳定判据可知本文提出的滞环控制Buck变换器具有良好的稳定性能。

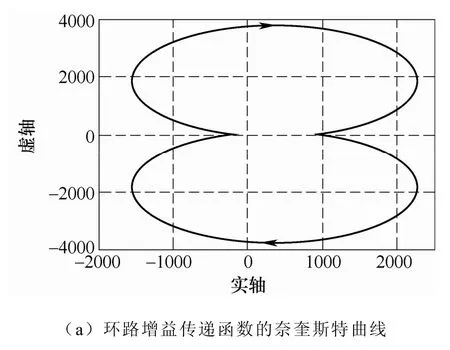
图8 环路增益传递函数的奈奎斯特曲线及在（-1, i0）放大Fig.8 Bode Nyquist diagram of loop gain transfer function and the amplification region at point (-1, i0)

图9 环路增益传递函数的极点分布图Fig.9 The pole distribution of loop gain transfer function

然后根据表中的电路参数，对提出新型滞环控制 Buck变换器电路进行了频域仿真，并与传统电压型控制方法的频域仿真结果进行了对比。

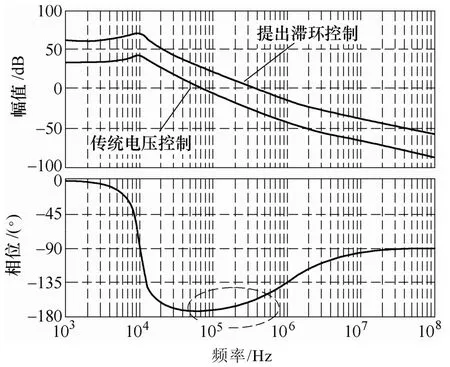
图10 环路增益T的传递函数Fig.10 Bode diagram of the loop gain T

图10为提出的滞环控制和传统电压控制Buck变换器的环路增益传递函数。由图可知，在所有的频率范围内，提出滞环控制的增益比传统电压控制都要高，且具有高的截止频率，保持了较高的相位裕度，而高的相位裕度可以使外环的电路设计更加简单，从而得到高的闭环增益和高的闭环带宽。因此，本文提出的滞环控制 Buck变换器对控制信号具有更高的灵敏度，从而具有更快的响应速度。

图11为提出滞环控制和传统电压型控制Buck变换器的“输入-输出”传递函数。由图可以看出，在中低频范围内，提出滞环控制比传统电压型控制具有更低的增益，因此，提出的滞环控制比传统电压型控制的 Buck变换器具有更好的抗输入电压扰动能力。

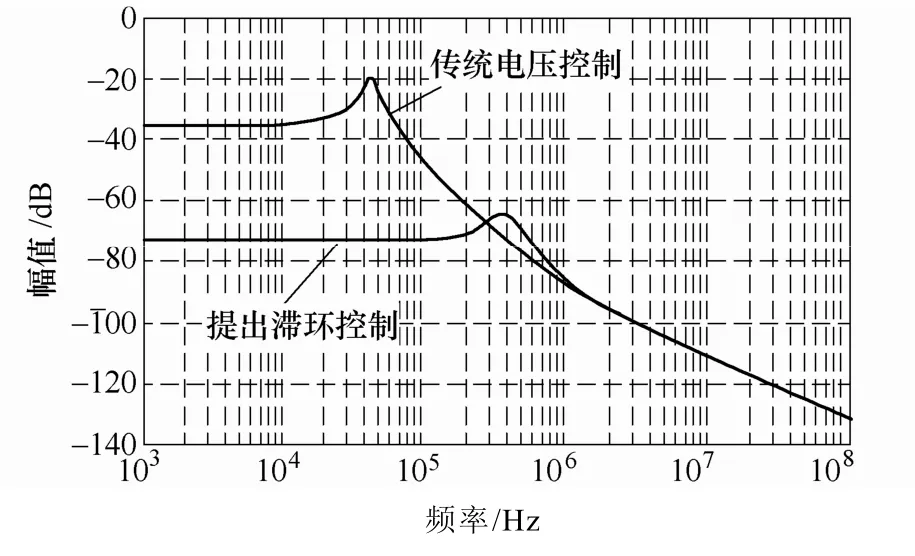
图11 输入-输出传递函数Fig.11 Bode diagram of input-to-output function

图12为提出滞环控制和传统电压控制Buck变换器的输出阻抗。从图中可以看出在高频段，两者具有相同的输出阻抗，这是因为在高频段，电路的输出阻抗主要是由输出滤波电容的寄生电阻决定的。而在中低频范围内，提出滞环控制较传统电压型具有更低的输出阻抗，因此具有更好的动态负载性能。

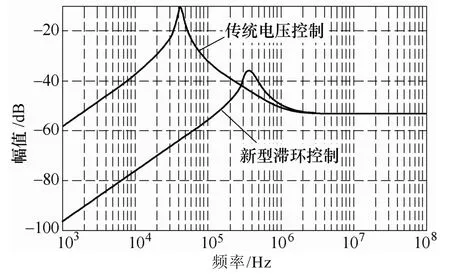
图12 输出阻抗Fig.12 Bode diagram of output impedance

3.2 实验分析

采用上表相同的电路参数，在实验样机上分别对提出滞环控制、传统电压型控制 Buck变换器进行了实验研究。

图 13给出了提出的滞环控制和传统电压型控制在负载跃降（2A→5A）和跃升（5A→2A）的瞬态响应实验图，从图中可以看出，提出滞环控制不仅有最短的延迟时间，而且具有最小的超调量。因此具有比传统电压型控制更优秀的负载动态响应特性。

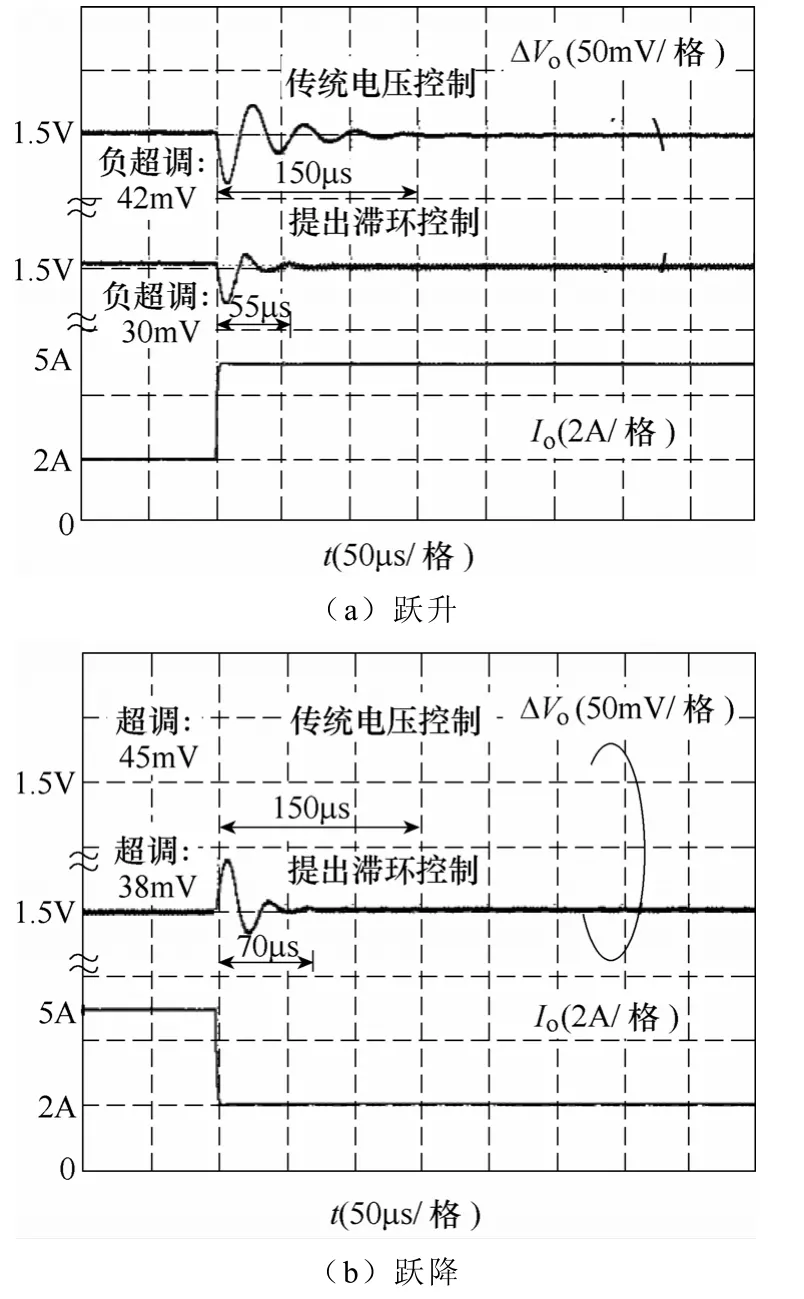
图13 负载跃降瞬态响应Fig.13 Transient response of load current

4 结论

本文提出了一种基于电容电荷平衡的滞环控制策略，该策略通过输出电压反馈对电容充放电来生成调制信号，控制电路简单，无需使用误差放大器及其相应的补偿网络，有效增强了控制电路的鲁棒性和瞬态响应速度。首先，利用状态空间平均法搭建其小信号模型，在此基础上，讨论了控制器参数对整个系统的影响，并和传统电压控制 Buck变换器进行了频域仿真和结果对比分析，最后通过实验进行了验证。仿真和实验结果表明，提出的滞环控制策略比传统电压控制 Buck变换器具有更快的瞬态响应速度和更好的抗干扰能力。

[1] Mammano R. Switching power supply topology voltage mode vs. current mode[J]. Elektron Journal-South African Institute of Electrical Engineers, 2001,18(6): 25-27.

[2] Soto A, Alou P, Cobos J A. Design concepts and guidelines for VRMs from a power stage perspective[C]. 2004 IEEE 35th Annual Power Electronics Specialists Conference, 2004, 3: 2218-2224.

[3] 王广柱. 抛物线法 PWM 电流控制新技术[J]. 中国电机工程学报, 2006, 26(16): 97-102.

Wang Guangzhu. A novel PWM current control technique using parabola function[J]. Proceedings of the CSEE, 2006, 26(16): 97-102.

[4] Feng G, Meyer E, Liu Y F. A new digital control algorithm to achieve optimal dynamic performance in DC-to-DC converters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1489-1498.

[5] 倪雨, 许建平, 王金平, 等. 滞环调制全局滑模控制 Buck变换器设计[J]. 中国电机工程学报, 2010,30(21): 1-6.

Ni Yu, Xu Jianping, Wang Jinping, et al. Design of global sliding mode control Buck converter with hysteresis modulation[J]. Proceedings of the CSEE,2010, 30(21): 1-6.

[6] 乔树通, 伍小杰, 姜建国. 基于无源性的滑模控制在 DC/DC 变换器中的应用[J]. 电工技术学报,2003, 18(4): 41-45.

Qiao Shutong, Wu Xiaojie, Jiang Jianguo. Application of passivity-based sliding mode control in DC/DC converters[J]. Transaction of China Electrotechnical Society, 2003, 18(4): 41-45.

[7] 王凤岩, 许建平, 许峻峰. V2控制Buck变换器分析[J]. 中国电机工程学报, 2005, 25(12): 67-72.

Wang Fengyan, Xu Jianping, Xu Junfeng. Modeling and analysis of V2 controlled Buck converter[J]. Proceedings of the CSEE, 2005, 25(12): 67-72.

[8] 贺明智, 许建平, 吴松荣. 基于前缘调制的数字 V2控制[J]. 西南交通大学学报, 2007, 42(4): 484-489.

He Mingzhi, Xu Jianping, Wu Songrong. Digital V2 control of DC-DC switching converters based on leading-edge modulation[J]. Journal of Southwest Jiaotong University, 2007, 42(4): 484-489.

[9] Zhao J, Sato T, Nabeshima T, et al. A new PWM control scheme using a triangle waveform modulated by output voltage[C]. Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, APEC'04,2004, 1: 399-403.

[10] 华晓辉, 林维明, 熊代富. DC/DC变换器快速动态响应分析[J]. 电力电子技术, 2007, 41(1): 83-85.

Hua Xiaohui, Lin Weiming, Xiong Daifu. Analysis of fast transient response in DC/DC convertors[J]. Power Electronics, 2007, 41(1): 83-85.

[11] 刘晓东, 蒋昌虎, 邱亚杰, 等. BUCK变换器动态过程电容充放电平衡控制策略[J]. 电机与控制学报,2010, 14(6): 77-82.

Liu Xiaodong, Jiang Changhu, Qiu Yajie, et al. A control algorithm based on capacitor charge balance during transient for BUCK converter[J]. Electric Machines and Control, 2010, 14(6): 77-82.

[12] Wu Xiaohui, Wu Xiaobo. Adaptive hysteresis window control (AHWC) technique for hysteretic DC-DC buck converter with constant switching frequency[C].Asia-Pacific Power and Energy Engineering Conference(APPEEC), 2010: 1-4.

[13] Feng G, Meyer E, Liu Y. A new digital control algorithm to achieve optimal dynamic performance in DC-to-DC converters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1489-1498.

[14] 徐德鸿. 电力电子系统建模及控制[M]. 北京: 机械工业出版社, 2006.

[15] 胡寿松. 自动控制原理简明教程[M]. 北京: 科学出版社, 2008.