基于GPC和DOB的直驱XY平台鲁棒跟踪控制

赵希梅 赵久威 李洪谊

（1. 沈阳工业大学电气工程学院 沈阳 110870 2. 中国科学院沈阳自动化研究所 沈阳 110016）

1 引言

近些年来，高精度定位技术在数控加工领域得到了飞速发展，特别是以XY精密平台为代表的平面定位系统，是数控加工设备的重要组成部分，广泛应用于工业制造业[1]。由于现代工业对位置定位系统的定位精度要求越来越高，其定位精度已从过去的毫米级提升到微米级。因此，随着定位精度要求的提高，位置定位系统的设计与实现也越来越困难[2]。

为了保证XY平台的伺服性能，一方面，要保证系统有快速精确的跟踪能力，另一方面，要对未知的扰动信号有较强的鲁棒性[3]。目前广泛应用的PID控制器很难满足其需要，提出了许多现代控制算法，如鲁棒控制，预测控制，模糊神经网络，滑模变结构控制等[4]。

GPC是20世纪80年代提出的一种现代控制算法，与其预测控制相比，该算法基于参数模型，模型参数少[5]。GPC是在自适应控制中发展起来的，它保留了自适应控制的一些优点。在具体实现上，采用多步预测、滚动优化和反馈校正策略，系统具有很好的跟踪性能，适合工业生产过程控制[6,7]。在具体实现上，广义预测控制方法多应用惯性大的机械运动控制系统。本文采用GPC作为直驱XY平台伺服系统的前馈控制器来提高系统的跟踪能力，对于XY双轴之间存在的系统参数不确定性以及各种非线性扰动，采用DOB进行抑制。DOB的设计思想是，将外部力矩干扰及模型参数变化造成的实际对象与参考模型输出差异等效到控制的输入端，即观测出等效干扰。在控制中引入等效的干扰补偿，实现对干扰的抑制。

2XY平台伺服系统轮廓误差分析

直驱XY平台是由两台进给方向相互垂直的直线永磁同步电机驱动组成，通过对两台电机的控制来完成平面位置定位，XY平台轮廓误差示意图如图1所示。

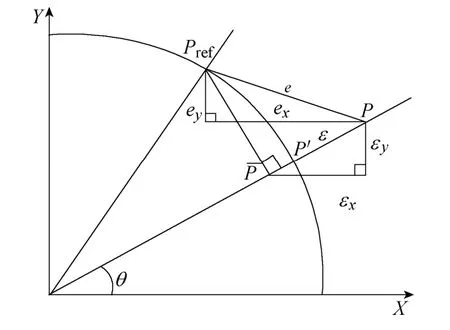
图1XY平台轮廓误差示意图Fig.1 Schematic diagram of theXY table contour error

图1中的圆弧为系统的参考轨迹，P为被控系统的实际位置，Pref为其参考位置，由于系统在双轴上都会有惯性延迟效应，因此会产生跟踪误差，图中P到Pref的距离e就定义为系统的跟踪误差，主要指动态误差，其中ex为其在X轴方向的分量，ey为其在Y轴的分量。

另外，扰动与XY双轴间的耦合，也是造成XY平台位置误差的主要因素，其体现为系统的轮廓误差，也就是系统的位置误差，如图中PP'所示，为了便于计算，可以用P来等效为轮廓误差，用字母ε表示，其中εx为其在X轴上的误差分量，εy为其在Y轴的误差分量。

因此，减小XY平台位置误差的方法有两种，一种是通过减小跟踪误差来间接地减小轮廓误差，另外一种是通过抑制扰动和解耦直接减小轮廓误差。本文所采用的GPC是通过提高系统的响应速度来减小跟踪误差，同时用 DOB抑制系统的外部扰动等不确定性因素的影响。

3XY平台伺服系统设计

基于GPC和DOB的XY平台系统控制框图如图2所示。GPC要在离散条件下设计，因此，需要将直线电机模型和扰动观测器进行离散化处理，图中yr(k)为参考输入值，H、F、pT和Δ为GPC的参数，u(k)为 GPC的输出。P(z-1)为被控对象的离散形式，Pn(z-1)为DOB中被控对象的参考模型，Q(z-1)为低通滤波器，ξ(k)为系统外部扰动，y(k)为系统输出。

图2 基于GPC和DOB的XY平台系统控制框图Fig.2 Block diagram ofXY table control system based on GPC and DOB

3.1 GPC设计

由于系统存在着输出滞后的问题，为了提高系统跟踪响应速度，采用GPC来设计前馈控制器。由于GPC对模型要求低，同时克服了传统自适应中极点配置对阶数不确定性敏感以及最小方差需要试凑控制量加权系数的缺点。其主要步骤包括：预测模型建立、滚动优化、反馈校正。

预测模型是描述系统动态行为的基础模型，在GPC中采用的是受控自回归积分滑动平均模型（CARIMA）。由于 CARIMA模型是离散的形式，因此，首先要将被控系统进行离散化得

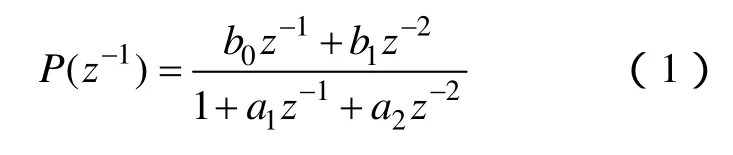
CARIMA模型可以表示为

式中，u(k)和y(k)表示被控对象的输入和输出；ξ(k)表示随机变量；Δ表示差分算子，其值为Δ=1-z-1，并且有

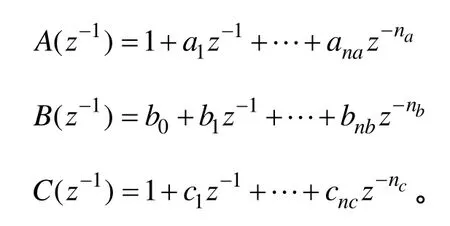
于是根据单轴直线电机的传递函数有：A=1+a1z-1+a2z-2、B=b0+b1z-1，为简化运算，取C=1。

由于直线电机伺服系统输入是可知的，所以为了使输出y(k)平稳到达设定值yr(k)，选择一阶滤波器

设计GPC的目的就是要使系统的输出值y(k+j)更靠近yr(k+j)。

目标函数的选择如下：

式中n——最大预测长度；

m——控制长度；

λ(j)——加权系数。

在选择这些参数时，既要保证系统有效，又要使其便于运算，当最大预测长度、控制长度和加权系数确定后，要使用丢番图（dioaphantine）方程来预测超前j步的输出为

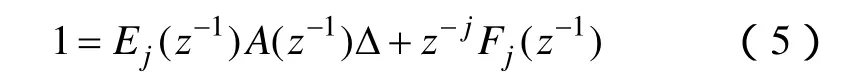
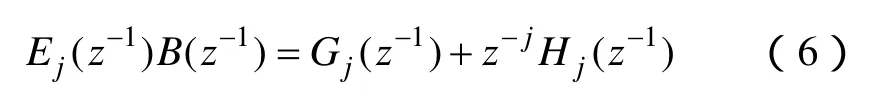
式中

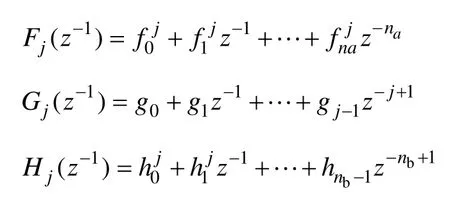
根据式（2）、式（5）和式（6）得

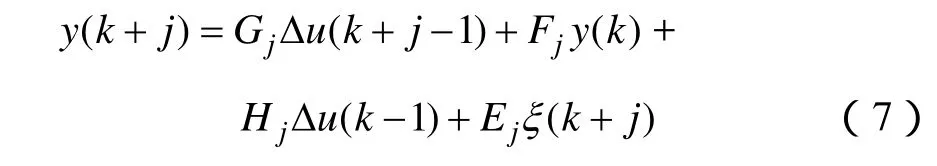
将其改写成向量形式为

定义

则目标函数可以重新表示为

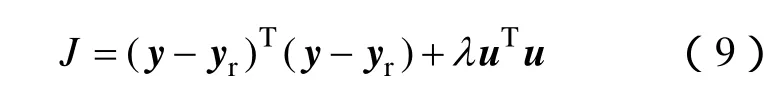
将式（8）代入式（9）后，计算J的最小值，即∂J∂Δu=0 ，得

GPC的控制率可写为

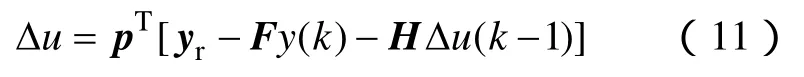
式中，pT为 (GTG+λI)-1GT的第一行。

在GPC中，虽然没有直接给出反馈或闭环，但每一步，都要检测实际输出并与预测值比较，以便修正预测的不确定性。当系统存在非线性、时变、扰动时，这种反馈能及时修正预测值，这样就降低了对基础模型的要求。本文选择n=m=2，设置加权系数λ(j)=0.001，则 GPC控制系统结构框图如图 3所示。

图3 GPC控制系统结构图Fig.3 The structure diagram of GPC control system

3.2 DOB设计

XY平台在运行过程中，两轴间会互相影响，同时系统也会受到其它未知扰动，这里采用 DOB加以消除或削弱。DOB的基本思想是将外部干扰和参数变化等所产生的实际对象与参考模型的输出之间的差异等效到输入端，即观测出等效干扰，在控制中加入等效干扰补偿，实现对误差的抑制[8,9]。DOB原理框图如图4所示。

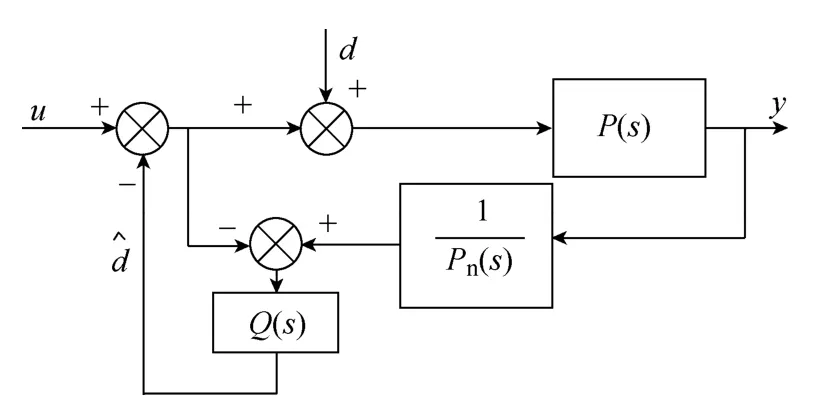
图4 DOB原理框图Fig.4 The principle diagram of DOB

P(s)为被控对象的传递函数，Pn(s)为其参考模型，d为等效干扰，为观测出的干扰，y为控制器输出，u为被控系统的输入，Q(s)为一低通滤波器。从图中可以看出，在通入低通滤波器之前的值为

然而在系统实际运行中还存在一些问题，被控系统的精确模型无法得到，参考模型不能与系统模型完全一致；测量噪声也会影响 DOB的性能。由于存在这些问题，需要在 DOB中引入一个低通滤波器Q(s)是非常重要的，Q(s)的性能好坏直接决定着DOB的动态性能。当其阶数越高、带宽越宽时，DOB的响应速度越快，抑制扰动的能力越强，但是对扰动的灵敏度会降低，因此，要保证Q(s)的阶数要不小于Pn(s)的阶数。由于被控对象为二阶系统，因此Q(s)采用三阶进行设计。其表示如下：

带宽要在鲁棒性和抗扰动能力之间寻求折中，根据经验取τ=0.000 1。

4 系统仿真与实验结果分析

本实验采用的是北京慧摩森科技公司生产的LM22-26系列直驱XY平台，控制系统采用两套Elmo数字驱动控制器、深圳固高公司的 GE-200-SG-PIC-G型两轴高性能运动控制卡、MII1600光栅编码器。XY平台实验结构图如图5所示。

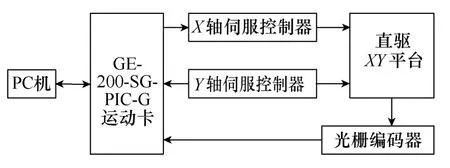
图5 实验结构图Fig.5 Experimental structure diagram

为验证所提出方案的有效性，将所提出的方法同PID控制相比较，对XY平台的双轴分别输入幅值为 1频率为π的正弦和余弦信号，将预测鲁棒控制系统进行仿真实验，GPC中取λ=0.001，DOB中取τ=0.000 1，PID选择Kp=200、KI=0.3。通过对X轴和Y轴进行仿真与实验，得到基于PID控制的系统跟踪误差曲线如图 6和图 7所示，基于 GPC和DOB的系统跟踪误差曲线如图8和图9所示。从图中可以看出，基于GPC和DOB控制的系统的位置误差非常小，具有更好的控制效果，表明系统具有良好的跟踪性能和鲁棒性能。

图6 基于PID控制的X轴位置跟踪误差曲线Fig.6 Position tracking error curve ofX axis based on PID control

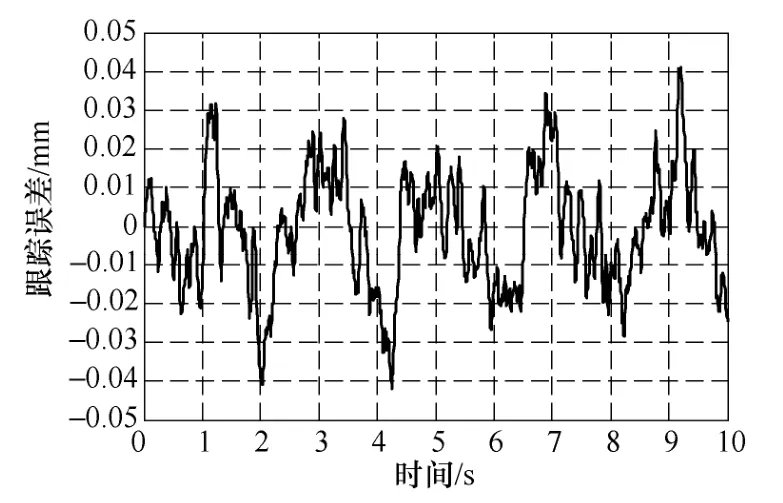
图7 基于PID控制的Y轴位置跟踪误差曲线Fig.7 Position tracking error curve ofY axis based on PID control

图8 基于GPC和DOB控制的X轴位置跟踪误差曲线Fig.8 Position tracking error curve ofX axis based on GPC and DOB control

图9 基于GPC和DOB控制的Y轴位置跟踪误差曲线Fig.9 Position tracking error curve ofY axis based on GPC and DOB control

5 结论

针对直驱XY平台伺服系统采用 GPC和 DOB相结合的控制方案，GPC通过模型建立，滚动优化，反馈校正，来提高系统的响应速度，同时加入DOB提高系统鲁棒性并将XY轴之间的耦合视为扰动进行补偿，通过GPC和DOB的结合，提高了XY平台的位置定位精度。仿真实验结果表明，该方法对提高控制系统的控制精度具有良好效果。

[1] 王先逵, 陈定积, 吴丹. 机床进给系统用直线电动机综述[J]. 制造技术与机床, 2001(8): 18-21.

Wang Xiankui, Chen Dingji, Wu Dan. Overview of linear motor used in machine tool feeding system[J].Manufacturing Technology & Machine Tool, 2001(8):18-21.

[2] 赵希梅, 郭庆鼎. 基于 ZPETC和 CCC的直驱 XY平台高精度控制[J]. 组合机床与自动化加工技术,2011, 2(2): 83-85.

Zhao Ximei, Guo Qingding. High precision control based on zero phase error tracking controller and cross-coupled controller for direct drive XY table[J].Modular Machine Tool & Automatic Manufacturing Technique, 2011, 2(2): 83-85.

[3] Kou Baoquan, Wu Hongxing, Li Liyi. Thrust characterristics investigation of double-side plate permanent magnet linear synchronous motor for EML[J]. IEEE Transactions on Magnetics, 2009(1): 501-505.

[4] Chen S L, Hsieh T H. Repetitive control design and implementation for linear motor machine tool[J].International Journal of Machine Tools and Manufacture,2007, 47(12): 1807-1816.

[5] Jose Vincente Salcedo, Miranzo Martinez. GPC robust design using linear and/or bilinear matrix inequalities[J]. European Journal of Control, 2007, 13(5): 451-467.

[6] Jianjun Shi, Atul G Kelkar. Feedback linearization based generalized predictive control of jupiter icy moons orbiter[J]. Journal of Dynamic Systems, Measurement and Control, 2009, 131(1): 1-10.

[7] Egiguren P A, Caramazana O B, Etxeberria J A C.Linear generalized predictive position control of induction motor drives[J]. IEEE Industrial Electronics Society, 2011: 1922-1927.

[8] Ales Hace, Karel Jezernik, Asif Sabanovic. SMC with disturbance observer for a linear belt drive[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6):3402-3412.

[9] Hideyuki Kobayashi, Seiichiro Katsura, Kouhei Ohnishi.An analysis of parameter variations of disturbance observer for motion control[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6): 3413-3421.