激光捷联惯导系统线振动基座下误差参数辨识仿真
李 闯,苏 展
(中国人民解放军92941 部队,辽宁 葫芦岛 125000)
0 引 言
激光捷联惯导系统是将惯性器件(激光陀螺和加速度计)直接固连在载体上的一种自主导航系统,在航空、航海等军事领域有着重要的应用价值[1]。由于惯性器件的误差对系统导航精度具有重要影响,为了提高系统导航精度,一种方法是进一步提高惯性器件的精度,另一种方法是对惯性器件的误差进行数字补偿。目前,进一步提升惯性器件的精度越来越困难,而且成本较高,因此,误差补偿技术成为一种经济并高效的方案[2]。误差补偿的前提是对误差参数进行有效辨识。目前,对静基座条件下的误差参数辨识研究较多,但对外加线振动激励下的误差参数辨识研究较少。而捷联惯导系统由于固连在载体上导致工作时往往存在复杂的振动,因此研究振动条件下捷联惯导系统的误差特性更具有现实意义[3]。本文利用MATLAB 设计卡尔曼滤波器,对线振动条件下的捷联惯导系统误差参数进行了计算机仿真。
1 线振动基座下卡尔曼滤波器设计[4 -6]
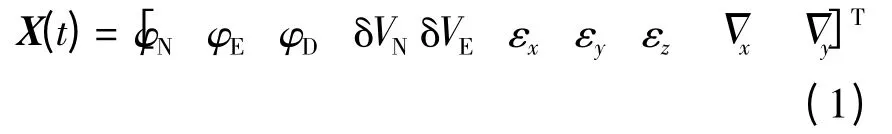
式中:φN,φE,φD分别为横滚误差角、俯仰误差角、偏航误差角;δVN,δVE分别为北向速度误差、东向速度误差;εx,εy,εz分别为X,Y,Z 轴方向上的陀螺漂移;ΔΔ分别为X,Y 方向上的加速度计零偏。
振动基座初始对准的状态方程为
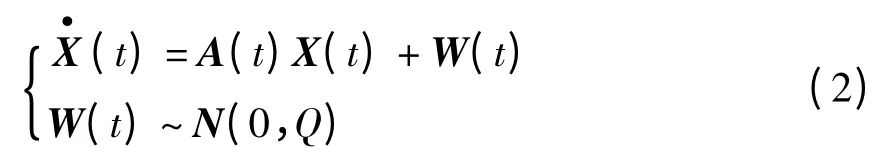
式中:系统激励噪声向量W(t)为高斯白噪声;
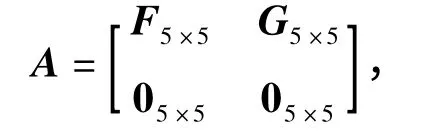
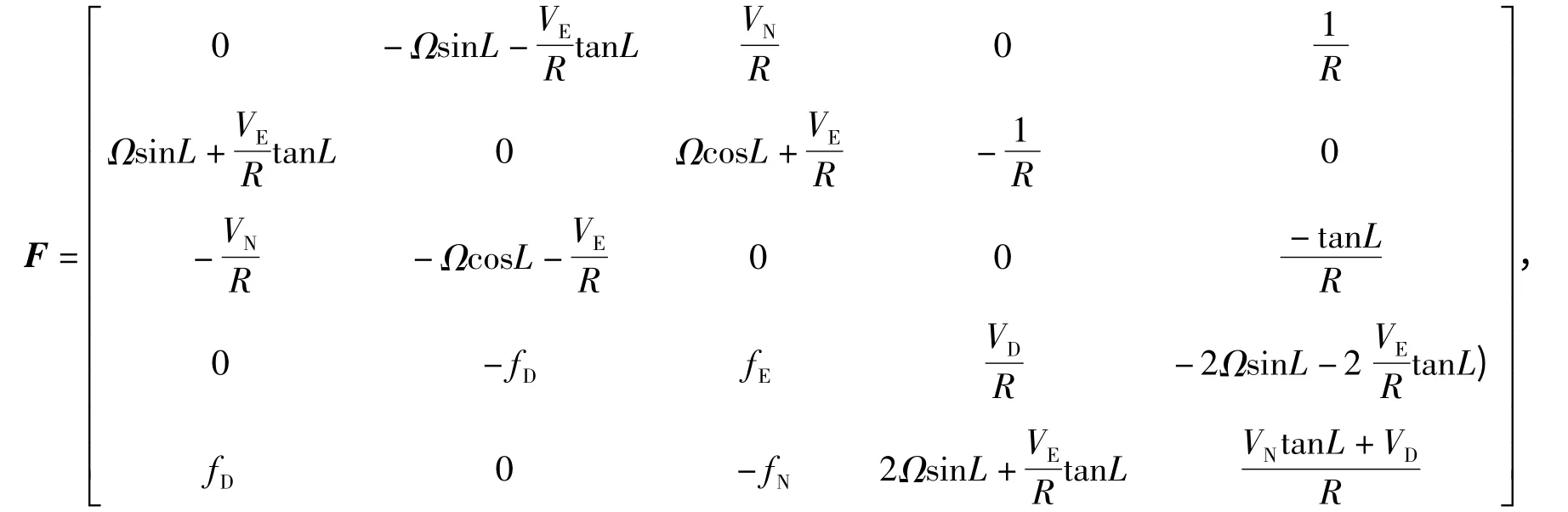
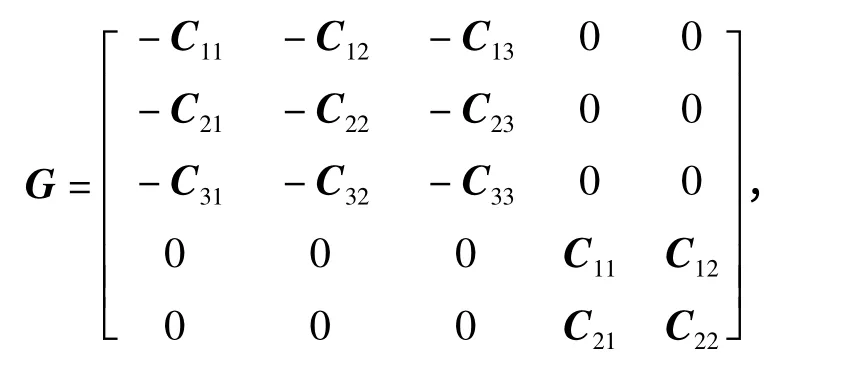
其中,VN,VE,VD分别为载体运动的北向速度、东向速度、地向速度,仿真中令VD以某一固定频率振动以模拟线振动环境。
L 为当地纬度;R 为载体到地心距离;fN,fE,fD分别为比力输入在导航坐标系(n 系)的分量,包括线振动和重力激励,仿真中将20 ms 的比力增量除以20 ms 求得比力fb;Ω 为地球自转角速率。
取量测量为Z(t)=[δVNδVE]T,建立系统的量测方程为
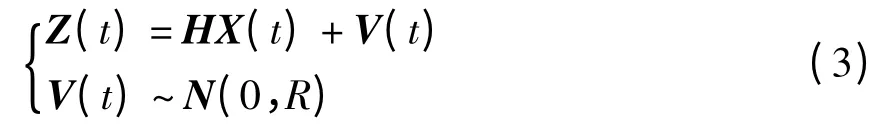
2 线振动基座下系统可观测性分析[7 -9]
系统的可观测性分析对于卡尔曼滤波器的设计有着至关重要的意义。研究表明[5],最优二位置对准能使系统完全可观测。本文基于最优二位置方案进行误差参数辨识,由系统的状态方程可以看出,当垂直方向存在变化的速度VD时,F(4,2),F(4,4),F(5,1),F(5,5)成为随时间变化的值,被估计量的信息在观测量中得到进一步反映,从而提高了系统的可观测度。
运用PWCS 可观测性分析理论,系统在每一个解算周期(0.02 s)近似为线性定常系统,其可观测矩阵Qi(i=1,2,3…)为
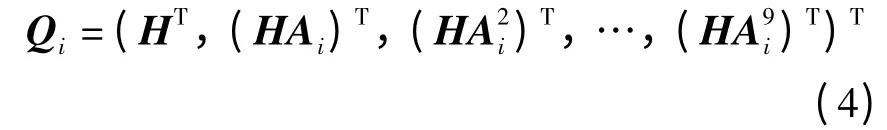
其中,Ai为任一解算周期的系统矩阵。系统的PWCS 提取可观测性矩阵Qs(i)可以表示为
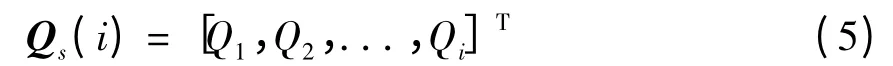
计算任一解算周期PWCS 提取可观测性矩阵的秩:

本文设计的滤波器是10 维的,因此式(6)说明振动条件下系统是完全可观测的,而最优二位置对准到第二位置才是完全可观测的,这在随后的计算机仿真中得到了进一步验证。
3 线振动基座下系统参数辨识仿真
利用MATLAB 进行仿真,仿真中陀螺常值漂移和随机漂移分别取0.01 (°)/h 和0.003 (°)/h,加速度计的常值偏置和随机偏置都为50 μg。由惯性器件仿真程序产生激光陀螺和加速度计增量数据,采样周期为0.01 s,在垂直方向引入线振动激励[10]:
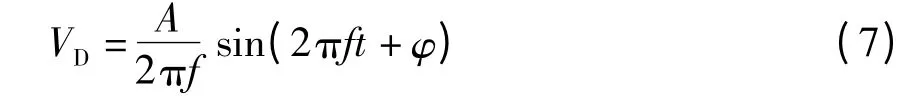
式中:A 为线振动加速度幅值,取为4g;f 为线振动频率,取为2 Hz;φ 为[0,2π]区间内均匀分布的随机相位。
仿真中模拟线振动基座对准和静态两种情况进行比较,采用最优二位置法。初始位置为北纬40.71°、东经120.99°,初始位置的姿态角设置为[φ,θ,ψ]=[0,0,40],初始姿态误差为[φN,φE,φD]=[0.01°,0.01°,0.03°]。初始速度为0,东向、北向速度初始误差均为0.1 m/s。滤波器的初始参数设置为
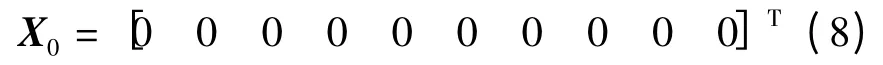
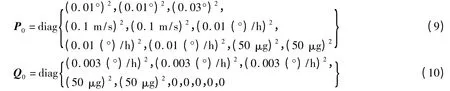
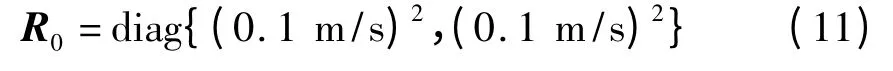
其中,P0,Q0,R0分别为离散化卡尔曼滤波器中初始估计误差方差矩阵,初始系统噪声矩阵和初始观测噪声矩阵。
滤波周期0.02 s,分两个位置进行滤波,第一个位置滤波完成,航向角改变180°进入第二位置,每个位置滤波时间为600 s。仿真结果如图1 ~3 所示。
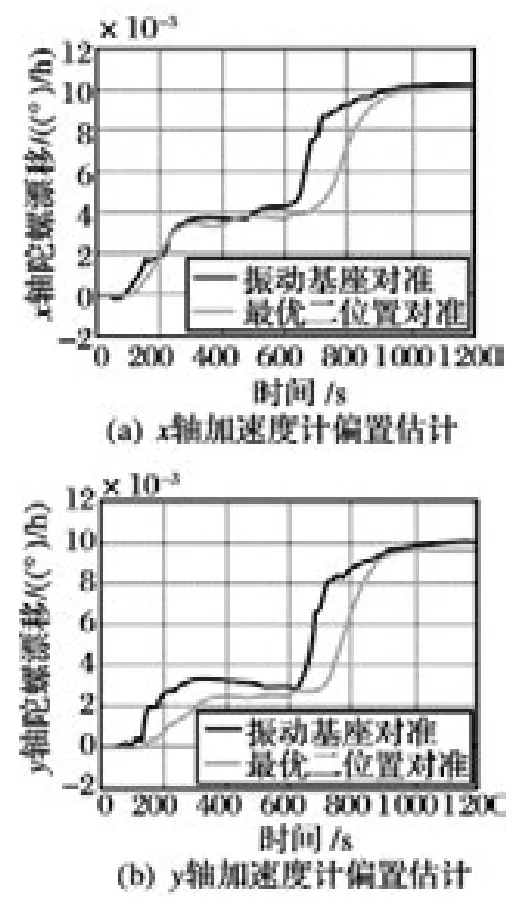
图1 水平陀螺漂移估计
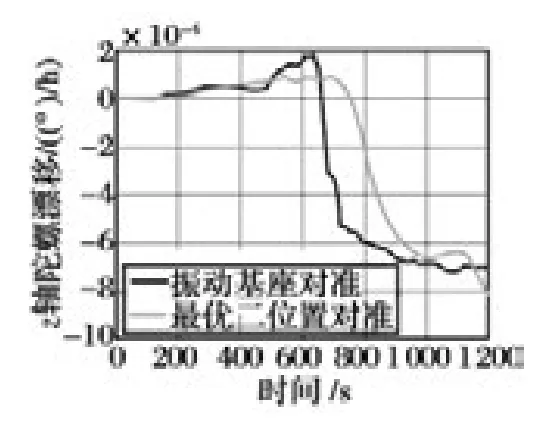
图2 z 轴陀螺漂移估计
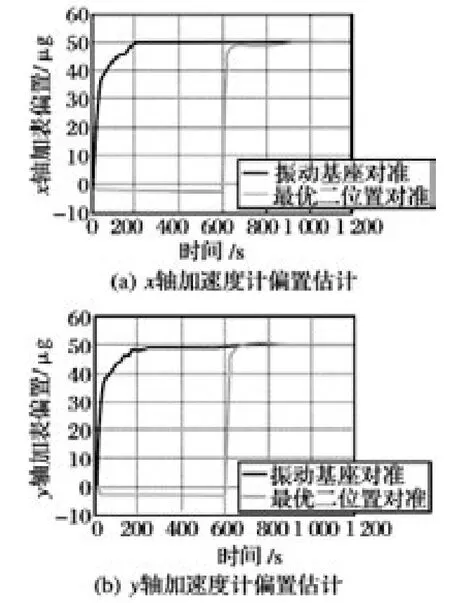
图3 加速度计偏置估计
由图1 可以看出,线振动基座对准过程中,水平陀螺(x 轴陀螺和y 轴陀螺)漂移的收敛速度比静态对准快,最终估计值也最接近真值。图2 表明,同水平陀螺相比较,两种情况z 轴陀螺漂移估计精度都较差,需要更长时间的估计才能达到理想的估计精度。
由图3 可以看出,线振动基座对准过程中,水平加速度计偏置的可观测度有了大幅度提高,其估计值在第一个位置就迅速收敛到真值,估计精度高,而静态情况则要到第二个位置才能收敛到真值。
仿真过程表明,线振动条件下系统的可观测程度明显改善,各参数的估计精度和速度都有提高,这与理论分析结果一致。
4 结 论
本文对振动与静态基座下激光陀螺捷联惯导系统的误差参数辨识进行了仿真对比,结果表明:振动基座下,水平陀螺漂移收敛速度快于静态基座对准,最终估计精度相当。z 向陀螺漂移收敛速度稍优于静态基座;水平加速度计偏置误差的收敛速度在振动基座下是静态基座下的2 倍,收敛速度得到大幅提高,最终收敛精度也明显优于静态基座。因此,线振动环境下,导航系统的误差辨识度更高并且更符合捷联惯导系统的应用环境,具有较高的应用价值。
[1]管叙军,王新龙. 捷联惯导系统动基座传递对准匹配方法[J]. 航空兵器,2014(2):3-8.
[2]邱宏波,周章华. 光纤捷联惯导系统高阶误差模型的建立与分析[J]. 中国惯性技术学报,2008,16(1):1-7.
[3]邓正隆,徐松艳,付振宪. 线振动条件下平台漂移误差模型参数辨识仿真研究[J]. 中国惯性技术学报,2002,10(6):45-49.
[4]于海龙. 提高振动环境下激光陀螺捷联惯导系统精度的方法研究[D]. 长沙:国防科技大学,2012.
[5]张红良. 陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D]. 长沙:国防科技大学,2010.
[6]秦永元. 卡尔曼滤波与组合导航原理[M]. 西安:西北工业大学出版社,1998.
[7]Lee J G,Park G G,Park H W. Multiposition Alignment of Strapdown Inertialnavigation System[J]. IEEE Transactions on Aerospace and Electronic Systems,1999,29(4):1323-1328.
[8]Goshen-Meskin D,Bar-Itzhack I Y. Observability Analysis of Piece-Wise Constant Systems Part I:Theory[J]. IEEE Transactions on Aerospace and Electronic Systems,1992,28(4):1056-1067.
[9]万德钧,房建成. 惯性导航初始对准[M]. 南京:东南大学出版社,1998.
[10]吴赛成. 船用高精度激光陀螺姿态测量系统关键技术研究[D]. 长沙:国防科技大学,2011.

