基于小波去噪与DRNN的光纤陀螺随机误差建模研究
王庆贺
(中国空空导弹研究院,河南 洛阳 471009)
0 引 言
陀螺仪的测量精度直接影响导航系统的性能,对其误差的研究至关重要。陀螺的误差可分为系统性误差与随机性误差,其中又以具有复杂特性的随机误差作为研究的重点。随机误差为有害噪声,为减小或者消除随机误差对惯导系统的影响,必须研究随机误差的特性并建模。随着随机误差理论研究的不断发展,Allan 方差、ARMA、小波理论、神经网络等方法已经被应用到陀螺的随机误差分析和建模中[1-4]。目前常用的陀螺随机误差模型有白噪声与有色噪声的组合模型、ARMA 模型、神经网络模型等。然而陀螺的随机误差是复杂的噪声复合,既有白噪声又有不同特点的有色噪声,低频噪声与高频噪声并存,且其时序数据通常为非平稳数据。这种复杂的特性使随机误差的建模存在建模难度大和建模精度不高等问题。针对这些问题,建模时选取不同的理论方法来组合应用,取得了良好的效果。例如在时间序列研究中,小波理论和ARMA 方法是最常用的组合[5-7],这对陀螺随机误差的建模具有借鉴意义[8-10]。但ARMA 模型为线性模型且建模操作复杂,相对于ARMA 建模,神经网络具有任意非线性映射的能力。对角神经网络(DRNN)是一种局部内递归神经网络,结构简单且具有良好的动态特性,利用其建模时,不必如ARMA 一样进行模型假设,简化了建模过程。
因此,本文采用这种理论组合的思路,选择小波阈值去噪和DRNN 对陀螺随机误差进行建模。首先,根据陀螺随机误差的特点,将其分为高频部分和低频部分;然后,采用小波去噪方法去除高频噪声,减小误差的复杂程度,再用DRNN 对去噪后的低频部分进行建模;最后,对陀螺的实测数据进行仿真分析,结果表明本文所提出的建模方法是行之有效的。
1 基于小波分析的阀值降噪
1.1 小波变换
小波变换是一个在时频域上都具有良好的局部特性的小波函数和一个平方可积函数的内积[12],如式(1)所示:
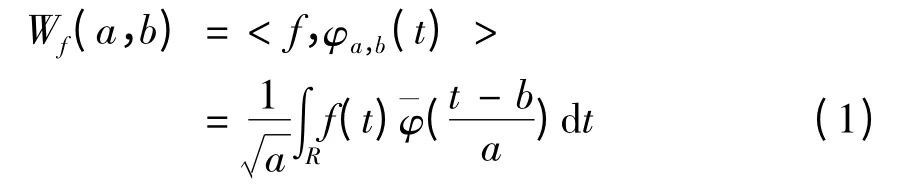
其中:f(t)为原始信号;φa,b为小波序列,称为小波;a(>0)为尺度因子;b 为位移因子;表示复数共轭。φ(t)通过a,b 进行伸缩和平移。位移因子b 起着平移作用。尺度因子a 不仅会改变φa,b的频谱结构,还会改变窗口的大小和形状。a 大时,对应低频部分,频率分辨率高,时间分辨率低;反之,对应高频部分,频率分辨率低,时间分辨率高。
在实际应用小波变换时是必须离散化的。可取整数m,n,取常数a0>1,b0>0,对a,b 进行离散化处理,如式(2)所示:

通常取a0= 2,b0= 1,称为二进小波变换,此时离散小波函数如下:
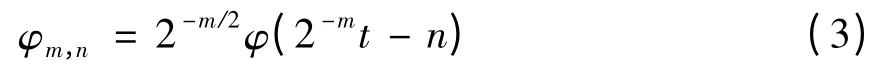
相应的离散小波变换为
天津市高等学校师资培训中心(以下简称天津市中心)成立于1990年,受天津市教委和天津师范大学双重领导。中心下设行政办公室、岗前培训办公室、信息技术部、教师资格认定办公室,当前业务以岗前培训、教师资格认定、高校教师网络培训为主。
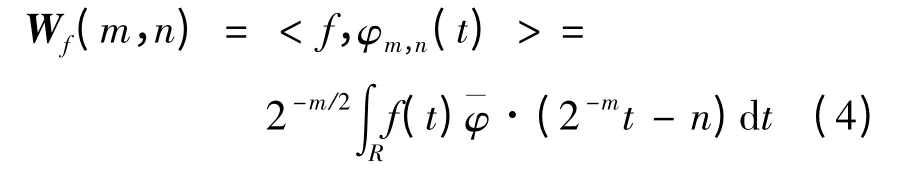
小波变换常采用Mallat 算法[11]。Mallat 算法为一种塔式分解算法,分解算法如下:
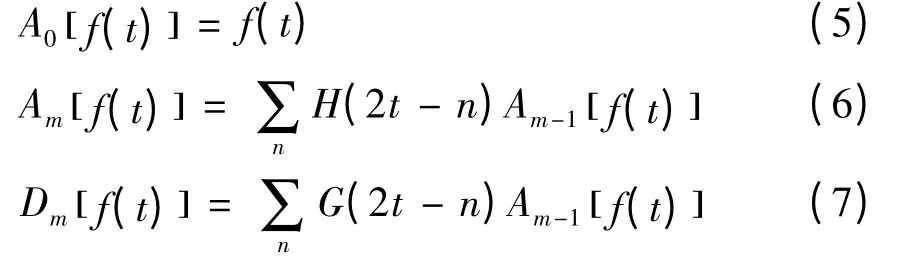
其中:f(t)为原始信号,t = 1,2,3,…,Τ;m 为小波变换分解层数,m = 1,2,3,…,M,其中M =log2Τ;H,G 分别为低频分解滤波器系数和高频分解滤波器系数;Am,Dm分别为分解得到的低频小波系数和高频小波系数。Mallat 算法的重构如下:
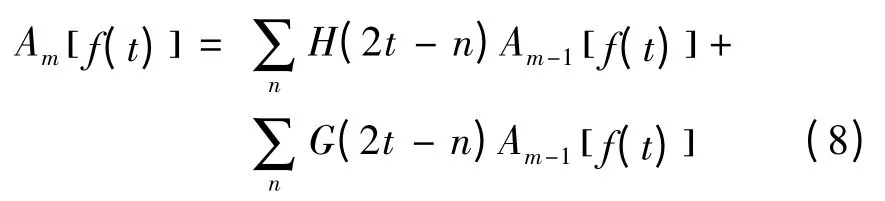
1.2 小波阀值去噪
小波去噪方法可分为三大类[11]。第一类为小波变换模极大值去噪;第二类为基于小波变换的相关去噪;第三类为阀值去噪,为最常用方法。小波阀值去噪基于多分小波变换:不同尺度的小波变换会表现出不同的形态,构造出相适应的规则,以减小甚至完全置零噪声产生的系数,同时最大限度保留有用信号的系数。小波阀值去噪的步骤归纳如下:
(1)选取合适的小波基函数和分解层数,对信号进行小波分解;
(2)根据信号和噪声的不同频率特点,对分解得到的系数进行阀值量化。小波变换较为细致地划分了信号不同频率成分,在不干扰有用信号的基础下,对噪声系数进行阀值量化完全可行;
(3)重构信号。
小波阀值去噪的关键是如何选取阀值,如何进行阀值的量化。对于阀值确定规则,阀值量化方法,文献[11]有非常全面的介绍,在此不再赘述。
2 对角神经网络(DRNN)
对角递归神经网络(Diagonal Recurrent Neural Network,DRNN)为内部递归神经网络,其隐层神经元只接收自我延迟反馈且与其他同层神经元无反馈连接。相比全局反馈递归网络(如Elman 网络等),DRNN 的结构更简单,这使其在保留动态映射能力的同时有更快的学习速度。DRNN 的网络结构如图1 所示。
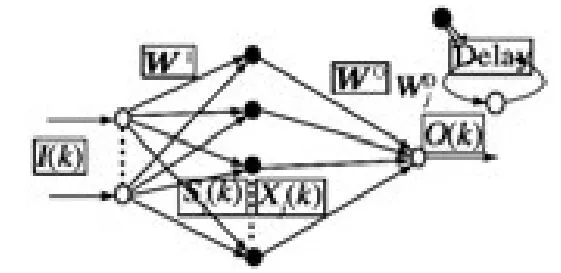
图1 DRNN 结构图
图1 所示为三层DRNN 网络,设输入神经元为n个,隐层神经元为h个,一个输出神经元。DRNN的数学模型如下:
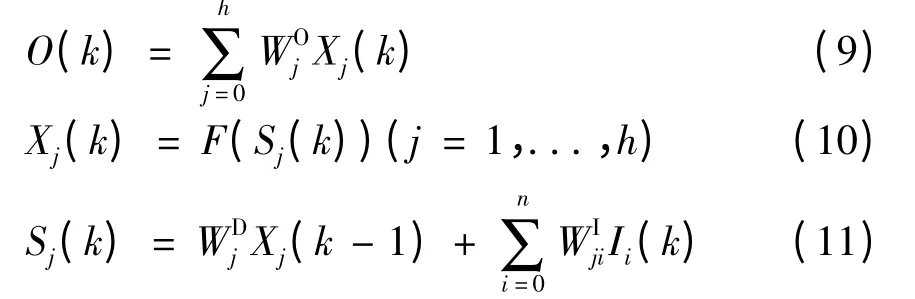
式中:O(k)为DRNN 输出;Sj(k),Xj(k)分别为隐层第j个神经元的输入与输出;Ii(k)为第i个输入神经元的输入;下标为零输入的代表偏置输入,赋值为1。WI为输入层至隐层的权值矩阵与偏置值;WO为隐层至输出层的权值矩阵与偏置值;为隐层神经元自反馈的权值与偏置值。隐层神经元F(x)取S 函数,输出神经元取purelin 函数为激活函数。
建模时,I(τ)为DRNN 网络τ 时刻的输入,为了进行预测,取其中)代表t 时刻输出的估计值,且有n = 2。如此可使输出为1)的函数,且不必如外递归网络或ARMA 确定模型的阶次[13]。此时网络输出为τ 时刻期望输出的估计值,从而实现预测。
DRNN 的学习算法可使用通过时间的反向传播(BPTT)算法(BP 算法扩展形成的)。此外,引入LM 算法优化网络的训练会比单独使用BP 算法有更快的收敛速度[14]。本文采用适用于DRNN 的LMBP 算法为训练算法。
对于DRNN 网络,数学描述如式(9)~(11)所示。取性能函数如下:
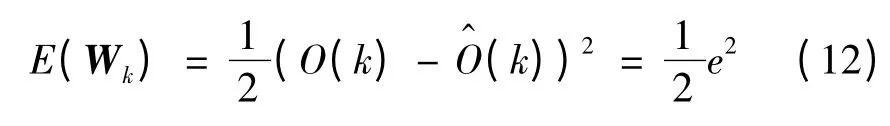
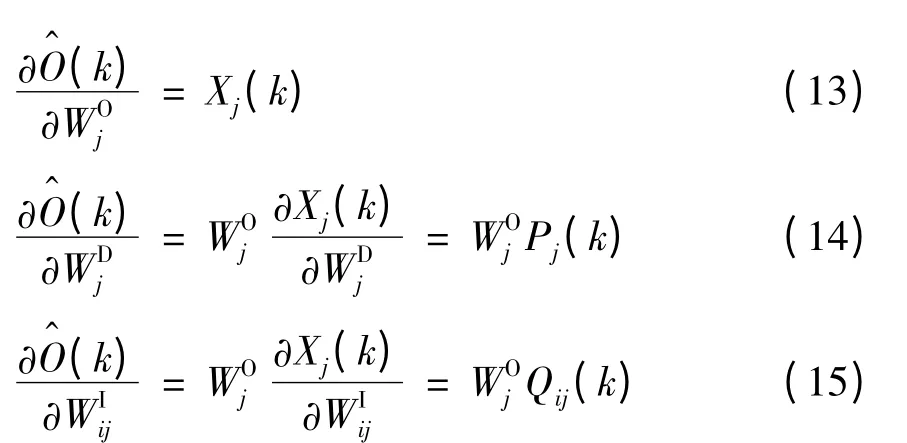
其中,
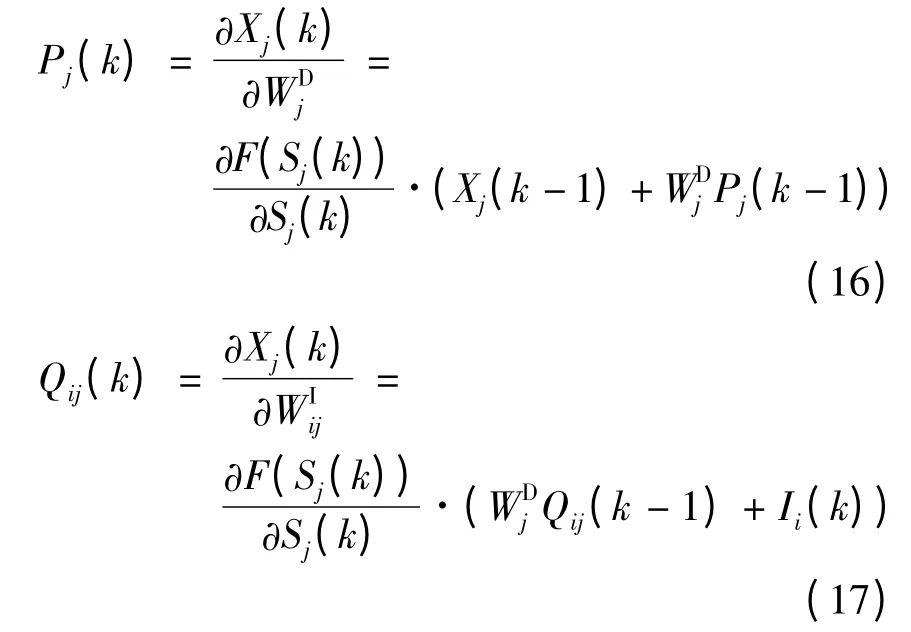
由式(12)~(17)可以求得雅可比矩阵,从而推导出DRNN 的LM 算法。
3 基于小波去噪与DRNN 的随机误差建模仿真
由于工作原理和环境干扰等原因,光纤陀螺存在多种确定性误差和随机性误差,输出信号是非平稳且弱非线性的,传统去噪方法效果并不理想。陀螺随机误差主要包括量化噪声,角度随机游走,零偏不稳定性(1/f 噪声),角速率随机游走,速率斜坡,正弦分量等[15]。本文以光纤陀螺实测数据为基础,对随机误差进行分析。
图2 为一组光纤陀螺在静基座下X 轴的随机误差数据。陀螺采样周期为1 Hz,采样时间为7 h,现截取陀螺稳定运行后14 000 s 的数据。
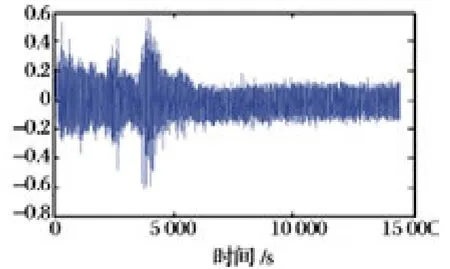
图2 光纤陀螺随机误差
对于所采集的随机误差数据,其特性可从时域与频域两方面进行分析。时域上,可采用相关性分析法;频域上,可进行功率谱密度(PSD)分析,能够更好的辨识出周期性误差。此外,Allan 方差方法是由David Allan 提出的,是一种时域分析方法,能够细致地对噪声统计特性的贡献进行表征与辨识,而且具有便于计算、易于分离等优点[16]。对于本组数据的分析结果如图3 ~5 所示。
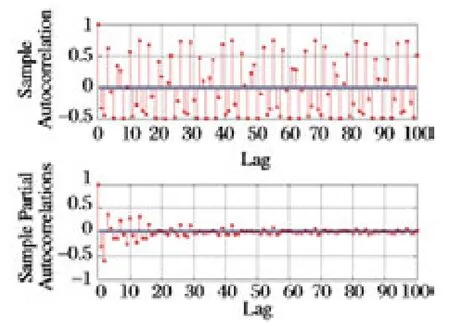
图3 随机误差相关性分析图
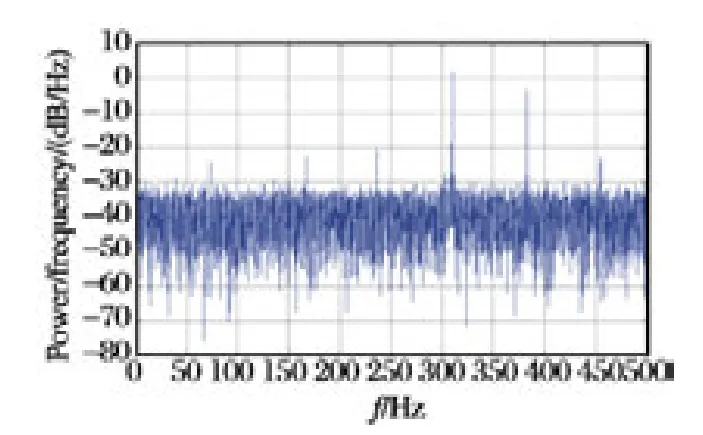
图4 随机误差PSD 分析
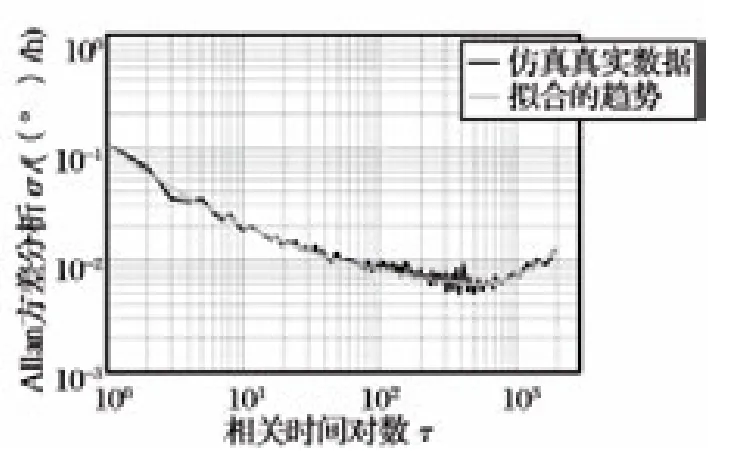
图5 Allan 方差分析
从图3 ~4 可以看到,随机误差自相关与互相关曲线都具有严重的拖尾现象,功率谱密度图出现尖峰,这说明随机误差里含有周期性噪声和有色噪声;图5 Allan 方差辨识结果也支持这一点结论,并且可以从图上更细致地辨识各种误差;数据中白噪声范围分布较广,周期性噪声集中在中高频部分,有色噪声一般集中在低频部分,可能会与集中在低频部分的有用信号混淆,很难从频域角度对其进行分离[17-18]。总之,多种复杂的噪声项使随机误差的建模非常繁琐且制约其精度。
小波变换能平稳化信号,基于小波多分辨的阀值去噪优于基于傅立叶变换的传统去噪方法。对角神经网络(DRNN)具有内递归特性和局部反馈特性,动态性能优于ARMA、前向神经网络,且节点少于全局反馈网络,有更好的动态性和实时性。本文采用这两种理论进行组合来处理陀螺随机误差并建模。首先对随机误差数据进行小波阀值去噪,滤除高频噪声;然后对去噪后的噪声进行DRNN 建模,并进行预测。
利用小波去噪需要选取小波基函数和分解尺度,在这两点确定后再进行阀值选取和量化。对于小波函数,综合考量计算量和去噪效果,经对比实验后选取sym4 小波;在分解层次大于4 尺度后,高频系数均值出现较大波动,所以选取分解尺度为4层。各层低频、高频系数如图6 所示;采用软阀值去噪,效果如图7 所示,经去噪后,陀螺随机噪声方差从0.008 8 降到6.59e-4,降噪效果明显。
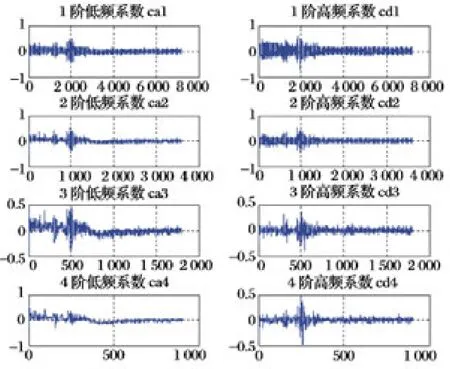
图6 小波分解各层系数
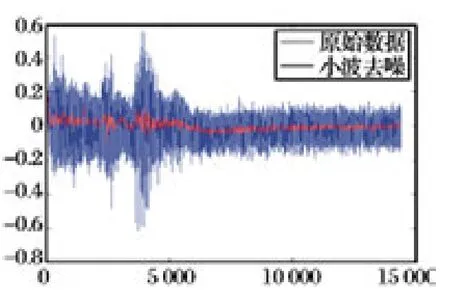
图7 小波去噪效果图
小波变换具有非因果性,且不具有平移不变性,不能实现时间序列的递推估计,这限制了小波去噪的在线应用。
从时间序列分析角度出发,研究对象的模型是非常有效的,大部分基于实验数据的建模都是以此开展的。利用神经网络对时间序列数据进行建模已经有不少的研究应用,其主要思想是仿照ARMA 模型方法进行非线性的建模[13],具有延迟的外部递归神经网络非常好的体现了这一特点。对角递归神经网络作为具有延迟的内递归神经网络,同外递归神经网络一样可以实现时间序列建模、预报,且不需要事先知道模型的阶次。小波去噪后,引入DRNN 对剩余的低频噪声进行建模,实现递推是可实现的。
本文采用具有3 层结构的DRNN,输入层含两个神经元,两个输入分别为当前时刻值和当前时刻的估计值;输出层含一个神经元,网络的输出为下一时刻的估计值;隐层神经元经多次实验后取15个。隐层神经元传递函数为S 型函数,输出神经元传递函数为purelin 函数。取去噪后2 500 组数据,对前500 组数据进行神经网络训练建模,后2 000 组数据进行验证。神经网络训练数据跟期望数据对比如图8 所示,2 000 组预测效果如图9 所示。
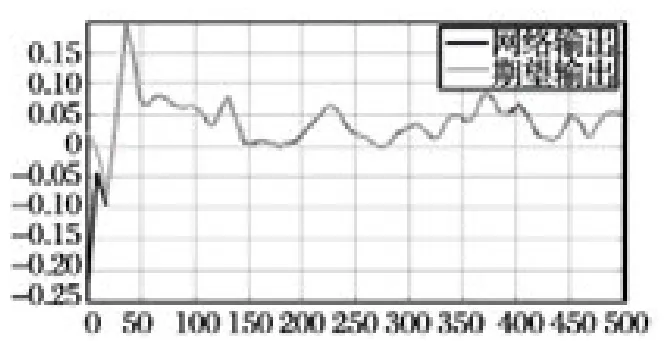
图8 神经网络训练效果

图9 神经网络预测效果
图8 中,低频部分经DRNN 建模采用LMBP 算法收敛速度非常快。从图9 可以看到DRNN 泛化能力较好,所预测的输出与期望的数值基本吻合。定量分析发现,DRNN 建模误差均值为-0.002 5,方差为4.387 0e-4;利用DRNN 模型进行预测的误差均值为-1.028 4e-4,方差为5.774 5e-5。并且经残差自相关与互相关分析发现,DRNN 模型的误差和预测的误差都为白噪声过程。
4 结 论
针对光纤陀螺随机误差,本文组合采用小波阀值去噪和DRNN 的建模并仿真验证。结果表明,采用这两种方法组合处理光纤陀螺随机误差,能够有效地对随机误差建模和补偿,从而提高惯导系统的测量精度。但同时,小波去噪和DRNN 建模都存在实时性较差的问题,需进一步研究相对应的快速算法以应对工程应用。
[1]El-Sheimy N,Hou Haiying,Niu Xiaoji. Analysis and Modeling of Inertial Sensors Using Allan Variance[J].IEEE Transaction on Instrumentation and Measurement,2008,57(1):140-149.
[2]李颖,陈兴林. ARMA 模型辨识及其在光纤陀螺漂移建模中的应用[J]. 系统工程与电子技术,2008,30(9):1752-1754.
[3]卢海曦,夏敦柱,周百令. 基于遗传小波神经网络的MEMS 陀螺误差建模[J]. 中国惯性技术学报,2008,16(2):216-219.
[4]梁莹,谈振藩,张庆,等. 一种光纤陀螺随机漂移的高精度建模方法[J]. 哈尔滨工程大学学报,2009,30(11):1251-1255.
[5]谷政,江惠坤.非平稳时间序列的小波混合方法及其应用[J]. 系统工程,2008,26(5):85-89.
[6]徐科,徐金梧.基于小波分解的某些非平稳时间序列预测方法[J]. 电子学报,2001,29(4):566-568.
[7]高静,李朝伟,董云峰,等. 空空导弹导引头小波降噪参数优选仿真研究[J]. 航空兵器,2010(5):48-54.
[8]李程,朱家海.基于小波和时间序列分析的陀螺随机漂移建模研究[J]. 弹箭与制导学报,2005,25(4):402-404.
[9]谢聂,朱家海. 非平稳时间序列的陀螺随机漂移数据处理方法[J]. 空军工程大学学报,2008,9(1):14-17.
[10]吴富梅,杨元喜.基于高阶AR 模型的陀螺随机漂移模型[J]. 测绘学报,2007,36(4):389-394.
[11]韩良军. 光纤陀螺的误差分析、建模及滤波研究[D]. 哈尔滨:哈尔滨工业大学,2008.
[12]张善文,雷英杰,冯有前. MATLAB 在时间序列分析中的应用[M]. 西安:西安电子科技大学出版社,2007.
[13]王科俊,王克成. 神经网络建模、预报与控制[M]. 哈尔滨:哈尔滨工程大学出版社,1996.
[14]Hagan M T,Demuth H B. 神经网络设计[M]. 戴葵,译. 北京:机械工业出版社,2002.
[15]毛奔,林玉荣. 惯性器件测试与建模[M]. 哈尔滨:哈尔滨工程大学出版社,2007.
[16]Hou Haiying. Modeling Inertial Sensors Errors Using Allan Variance[D]. Alberta:University of Calgary,2004.
[17]Nassar S,Schwarz K P,EI-Sheimy N. Modeling Inertial Sensor Errors Using Autoregressive (AR)Models[J]. Navigation,2004,51(24):259-268.
[18]Liu Luyuan,Chen Yuzhu,Chen Gang,et al. Model and Experiment Research on Gyro Drift Rate Based on Wavelet Transform[J]. Journal of Chinese Inertial Technology,2004,12(1):61-65.

