一种新的最优空基反弹道导弹中制导方法研究

刘浩敏

(中国空空导弹研究院，河南 洛阳 471009)

0 引 言

现代战争中，战术弹道导弹(TBM)以其速度快、突防能力强、破坏能力大等特点成为重要的威慑力量和纵深打击力量，因此，如何有效拦截弹道导弹已成为各军事大国关注的焦点。空基反导因具有部署灵活、响应速度快、拦截空域广等优点而倍受关注，如美国正在开展其空基反导作战平台—网络机载防御单元(NCADE)的研究，目前已取得了阶段性成果。此外，我国和俄罗斯也正在积极开展相关研究工作［1－5］。

弹道导弹从发射到命中目标整个过程一般可分为三个阶段，即上升段、中段和再入段。处于中段的弹道导弹位于大气层外，一般无机动能力，对此阶段的弹道导弹进行拦截具有得天独厚的优势，因此，为拦截器设计一种精确的中制导律至关重要。

目前，国内外许多学者在拦截制导律的研究方面作了大量研究。Ryoo 等人针对拦截动力学这一特殊仿射系统，设计了一种特殊控制李亚谱诺夫函数(CLF)，运用Sontag 控制理论给出了一种最优拦截制导律［6］，通过进一步研究该制导律的求解过程可以发现，要想实现目标拦截，即当相对距离r →0 时，拦截器需要极大的能量，这在拦截末端一般很难实现。Massoumnia 在文献［7］中提出了一种基于固定推进时间的最优中制导律，在动力学推导过程中，作者通过忽略拦截器和目标之间的重力差得到了一种简化的解析相对动力学模型，进而运用最优性原理解决了最优中段拦截问题。Newman 基于零控脱靶量(ZEM)的相关理论，根据不同的相对运动学模型给出了多种中制导律［8］，其中多数以非解析的形式给出，从而对弹载计算机的计算速度提出了较高要求。

本文在前人研究成果的基础之上，首先采用忽略拦截器和目标之间重力差多项式的近似处理方法，给出一种简化的弹－目相对运动学模型;其次，基于简化的弹－目相对运动学模型，运用LQR理论设计一种解析、闭环的燃耗最优中制导律，并根据给定的初始条件对所设计制导律进行数学仿真验证。

1 相对运动学模型

首先给出地心惯性坐标系的定义:坐标系原点取为地球中心，Ze轴沿地球自转轴，Xe轴和Ye轴位于地球赤道平面内，与Ze轴组成右手坐标系，其中，Xe轴指向春分点［9］。在该坐标系下，导弹和目标之间的相对几何关系如图1 所示。

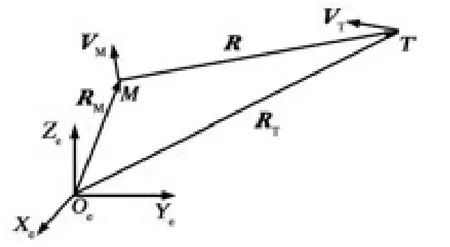
图1 导弹目标相对几何关系

图中，RM和RT分别为拦截导弹和目标在地心惯性系下的位置矢量;VM和VT分别为导弹和目标在惯性系下的速度矢量;R 和V 分别为目标相对拦截导弹的位置矢量和速度矢量。根据空间两质点之间的运动关系，在地心惯性坐标系下有如下两式成立:

其中，μ 为地球引力常数，其值为3.986 × 105km3/s2;rM和rT分别为RM和RT的大小;aC为作用于导弹上的控制加速度矢量。

根据式(1)～(2)，可以很容易给出大气层外导弹和目标之间的相对运动学方程为

其中，R = RT－RM。

研究式(3)发现，右端第二项RM的系数为导弹和目标之间的重力差，在实际拦截过程中，随着导弹和目标的逐渐接近，该重力差项的值越来越小，其对制导控制过程的影响越来越小。针对此重力差多项式，Newman 在文献［8］中给出了线性化、常数化等四种近似处理方案，考虑到中制导精度要求相对末制导低，本文采用了将重力差项常数化为0 的方案。

由此，可得到近似简化的弹－目相对运动学方程为

2 基于LQR 的最优制导律设计

根据目前较常见的反导方案，一般采用多级助推火箭，分初始制导段、中制导段和末制导段三个阶段以实现对大气层外的来袭弹道导弹进行有效拦截。初始制导段，根据GPS 提供的目标信息，第一级助推火箭将拦截器送到预定轨道高度，并使导弹具备一定的轨道速度;中制导段，第二级助推火箭将拦截器送到距离目标约10 km 远的位置，此时，拦截器探测装置开始工作并截获目标，动能拦截器弹离弹体。最后，动能拦截器通过自主探测装置实时获得目标，并通过飞控单元实时解算出制导指令，直至杀伤来袭目标。

根据拦截飞行方案，中制导律应实现末段拦截的初始制导环境，即使拦截导弹在中制导末段具有一定距离(Rf)和一定的相对速度(Vf)，从而确保拦截导弹具有足够的能量撞毁目标，最终实现动能拦截的目的。此外，考虑到拦截导弹携带燃料的有限性，制导律的设计应考虑燃耗最优。本节将在前面给出的简化弹－目运动学的基础上，运用LQR 最优理论对满足上述中制导要求的中制导律进行设计。

取两飞行器的相对位置矢量和相对速度矢量为参考状态，导弹的控制加速度矢量为控制输入，即X = ［R3×1V3×1］T，u = aC，则相对运动方程(4)可改写为如下形式:

其中，

现在，最优控制的设计问题就转化为在［0，∞］上求取反馈控制u*=－KX，使性能指标取极小。

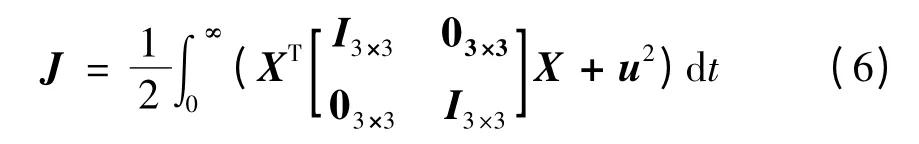
对于式(5)和(6)定义的LQR 问题，根据最优性原理可知，存在使上述系统渐进稳定的状态反馈控制u*=－R－1BTPX，其中，矩阵P = PT＞0满足如下Riccati 方程:

求解发现，上述方程存在负值根，考虑到被控对象的实际意义，舍弃负值解，得正值解为

式中，

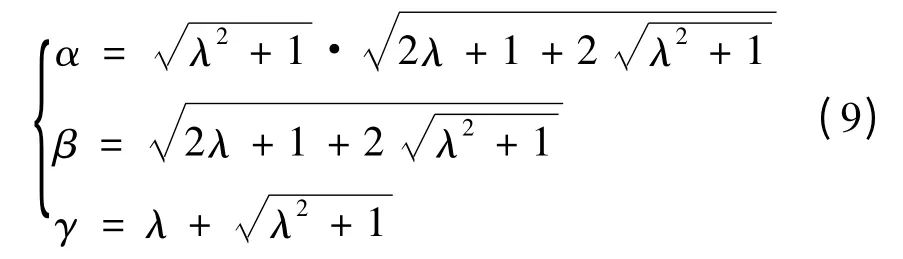
由此，可以得到最优状态制导律为

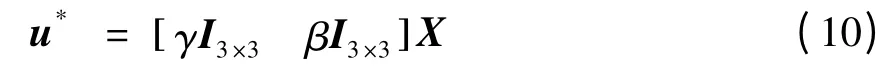
针对上述LQR 最优制导律，结合拦截实际过程，现做如下两点说明:

(1)对于拦截问题，拦截过程不可能持续无限长时间，否则视为拦截失败。式(6)中对积分时间取了无穷大，在工程上实际为一个动态过程的结束，且系统稳定要求末端状态趋近于零［10］。

(2)LQR 状态反馈控制u*=－KX 使系统渐进稳定，且使系统最终稳定在Xf= 0 点。显然，状态Xf= 0 不满足动能拦截条件。为了实现“定点、定速”这个拦截条件，可将期望的末段状态事先考虑到初始状态中，这样得出的控制指令u*实际上跟踪的轨迹就是期望轨迹，从而可实现“定点、定速”拦截制导要求。

3 仿真算例

为了对本文给出的制导律进行验证，以Matlab/Simulink 为仿真平台，参考文献［8］中给出的一组弹－目初始条件，如表1 所示，建立空基反导数字仿真模型对本文提出的中制导律进行数学仿真验证，如图2 所示。为了实现“定点、定速”拦截目标，假设拦截末端导弹和目标的期望相对速度和相对距离分别为1 km/s 和10 km(此数据可以根据实际要求设定)，根据上一节说明(2)，在进行具体数字仿真时，目标的初始速度和初始距离应考虑上述中制导期望末端条件。仿真结果如图3 ～5 所示。

表1 中制导拦截初始条件(地心惯性系)

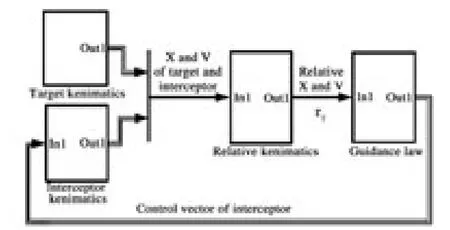
图2 空基反导数字仿真模型

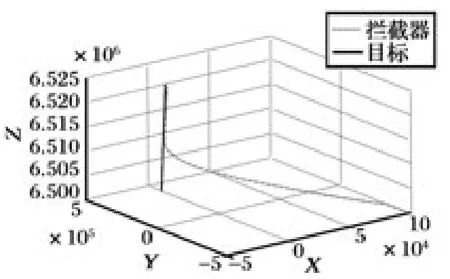
图3 弹－目运动轨迹仿真曲线

图4 弹－目相对位置和相对速度仿真曲线

从仿真结果可以看出，对于给定的拦截导弹和目标初始条件，本文提出的制导律可以在较短时间内实现定点定速的中制导拦截要求，进一步证明了本文第2 节对弹－目相对运动学近似处理的合理性。

此外，根据图5 所示拦截加速度仿真结果，由于处于中段的弹道导弹速度较高，要想对其进行有效拦截需要较高的拦截条件，即较大的动力系统支撑和较高的拦截初始速度及可靠的飞控系统保障。

图5 拦截导弹三个方向加速度曲线

4 结 论

本文基于简化的弹－目相对运动学模型，运用LQR 理论设计了一种新的能量最优、解析、闭环的拦截中制导律。为了验证所设计制导律的有效性，根据给定的弹－目初始条件，通过数字仿真对其有效性进行了验证。仿真结果表明，本文所设计的制导律既能满足空基反弹道导弹“定点、定速”的精度要求，也能满足能耗最优的要求，具有一定的理论研究和实际参考价值。

［1］谢鑫，李为民，黄仁金，等. 美军空基反导系统发展概述［J］. 飞航导弹，2011(10):48－52.

［2］肖曾博，雷虎民，张蓬蓬，等. 空基动能拦截弹制导控制系统建模与仿真［J］. 航空兵器，2012(2):9－15.

［3］单晓林，雷虎民，尚增博，等. 空基动能拦截弹寻的制导系统性能分析［J］. 航空兵器，2014(8):12－17.

［4］黄志理，崔颢，李萍. 美军机载导弹防御武器发展现状研究及启示［J］. 航天电子对抗，2012(28):1－3.

［5］周义. 俄罗斯反弹道导弹预警系统［J］. 现代军事，2012(2):27－28.

［6］Ryoo C K，Kin Y H，Tahk M J，et al. A Missile Guidance Law Based on Sontag’s Formula to Intercept Maneuvering Targets［J］. International Journal of Control Automation and System，2007，5(4):397－409.

［7］Massoumnia M A. Optimal Midcourse Guidance Law for Fixed-Interval Propulsive Maneuvers［J］.Journal of Guidance Control and Dynamics，1995，18(3):465－470.

［8］Newman B. Spaccraft Intercept Guidance Using Zero Effort Miss Steering［C］∥AIAA Guidance，Navigation and Control Conference，Monterey，CA，1993.

［9］钱杏芳，林瑞雄，赵亚男，等. 导弹飞行力学［M］. 北京:北京理工大学出版社，2000.

［10］刑继祥，张春蕊，徐洪泽. 最优控制应用基础［M］.北京:科学出版社，2003:133－136.