数据分析中不应忽视理性的价值
王卫东 潘淑芬
“统计与概率”是数学课程内容的重要组成部分,它贯穿于数学教学的各个学段。《数学课程标准》(2011年)明确指出,“数据分析是统计的核心”,然而,在统计教学的过程中,一些教师往往会花很大的精力去强调统计表、统计图的制作规范(如:要填写统计的时间、要在图表中标出相应的数据……),但对于数据的分析,却常常只是浅尝辄止,仅仅停留在简单的提问与解答上,缺少了师生间的深度对话,忽视了理性精神的塑造与培养。
理性是数据分析中不可忽视的核心价值,基于这样的认识,笔者在教学“折线统计图”(苏教版数学五年级下册第22页)中的“练一练”时,进行了如下教学尝试。
一、 在数据分析中树立宏观的意识
[教学片段一]
师:刚才我们研究了张小楠同学6~12岁的身高变化情况(教材中的“例1”),下面请你根据自己的身高数据,完成数学书中的“练一练”。
(学生根据自己课前搜集的一到五年级的身高数据,完成统计表、统计图。)

师:从一年级到五年级,你一共长高了多少厘米?从哪个年级到哪个年级,你的身高增长得最快?
……
师:听了大家的汇报,我们不难看出每个人的身高变化情况是有所区别的:有的人长得快,有的人长得慢,有的人长得早,有的人长得迟。通过这张统计图,我们能清晰地看出自己的身高变化情况,但是要想知道全班同学的身高变化情况,又该怎么办呢?
生:我们可以把全班同学的身高数据汇总到一起。
师:想法不错!下面我就把大家的身高数据汇总起来,看看男、女生的身高分别会有怎样的变化。(教师将课前搜集的学生身高数据导入Excel软件,先求出每个年级阶段男、女生的平均身高之后,再借助Excel软件制成复式折线统计图。)
师:观察这幅统计图,你有什么想说的?
……
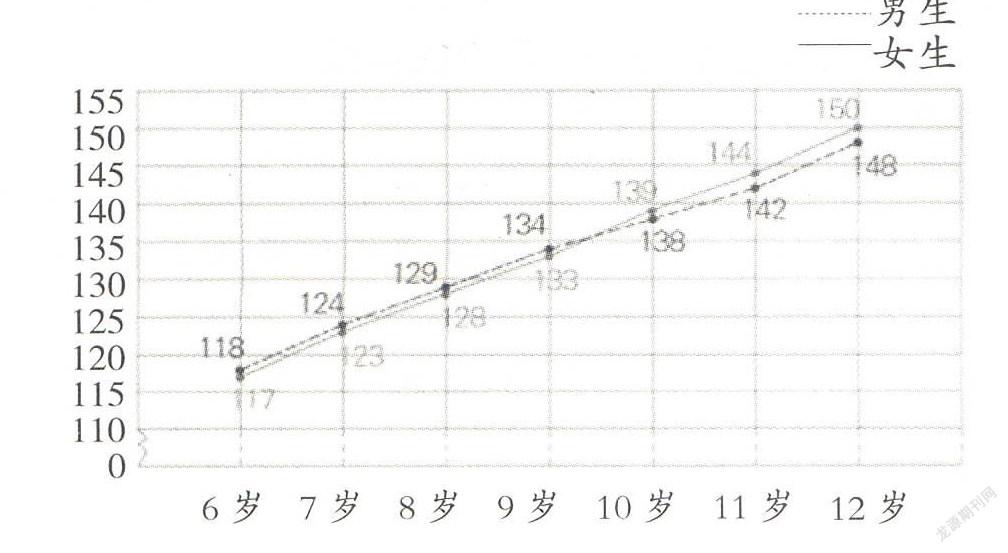
师:刚才大家讨论了全班男、女生平均身高的变化情况,如果有条件的话,我们还可以得到全年级、全校乃至更大范围内学生的身高变化情况统计图,这样我们就可以更好地从整体上了解小学生的身高变化情况了。瞧,这是经过抽样调查后得到的全国6~12岁小学男、女生平均身高统计图。
出示:
师:把你自己的统计图与我们班的统计图以及全国的统计图进行比较,你有什么发现?
……
教师总结:我们要学会用整体的眼光来观察事物或现象。
总体和总量是统计学中最基本的概念,虽然统计调查和处理都要从个体入手,但其最终目的是为了对现象的总体做出评价,因此,在统计教学中,我们有必要引导学生从宏观的角度对数据进行整体的审视与分析。在本课中,教师首先从每位同学的身高变化情况入手,进而研究全班男、女生的平均身高变化情况,最后呈现了全国男、女生的平均身高统计图,学生经历了从个体统计到群体统计的过程,在微观到宏观的视角转换间,他们感悟到了统计对象的差异以及统计活动的价值。不管是个体统计的整体分析,还是群体统计的整体把握,就统计教学而言,引领学生理性地站在宏观高度去分析数据,有助于学生更科学地去把握事物发展的趋势,探寻出事物发展的规律。
二、 在数据分析中感悟辩证的思想
[教学片段二]
师:你现在身高是多少?与我国同年龄的小学生平均身高比一比,怎样?
生(女):我身高是163厘米,高于全国平均身高。
师:你多少岁?
生:12岁。
师:12岁女生的全国平均身高是150厘米,你高出了不少啊!有没有比全国平均身高低的同学。
生(男):我身高145厘米,比全国男生的平均身高低3厘米,而且我10到12岁时的身高都比全国的水平要低。
师:我能理解你的感受,因为老师的个子也不高,但是你还是有希望的,同学们,你们知道为什么吗?
生1:他的年龄还小,还会长个子的。
生2:这里的平均身高是指全国的平均水平,并不是说每个人身高都会以这样的速度在生长,说不定,你是先长得慢,后长得快呢!
师:也就是说,有些学生的身高变化情况会有些特殊,是吗?
生:是的。
师:你(矮个子同学)听懂了吗?如果顺着刚才这位同学的思路,那么先长得快的同学看来也不能太得意了,说不定你是先长得快,后长得慢,甚至后来还不长了!
(同学们哈哈大笑起来。)
师:所以说,现在个子矮的同学不要气馁,个子高的也不要骄傲。既然身高变化的过程中存在着特殊情况,那么这张关于全国平均身高的统计图还有价值吗?
生3:有价值,这是全国的平均水平,也就是大部分同学的身高情况是这样变化的,而我们刚才讨论的是特殊情况,那毕竟是少数。
生4:全国统计图让我们有一个参照的标准,通过对比,我们可以知道自己是偏高、偏矮,还是正常,由此来调整自己的饮食和运动。
……
教师指出:我们要学会用辩证的眼光来分析数据。
在数据分析的过程中,理性的精神除了体现在数据的整体分析上,还体现在对个体数据的处理上。在上面的教学中,教师引导学生将自己的身高与全国小学生的平均身高进行对比,得出两个极端的结果:一个女生比平均身高高,一个男生比平均身高矮。如何处理这两个极端数据呢?教师通过“但是你还是有希望的,同学们,你们知道为什么吗?”“也就是说,有些学生的身高变化情况会有些特殊,是吗?”的引导,让学生感悟到事物围绕着平均水平发展的同时也会有一些特殊情况。接着,教师借助“既然身高变化的过程中存在着特殊情况,那么这个关于全国平均身高的统计图还有价值吗?”的追问,引领学生再次回到“全国6~12岁小学男、女生平均身高统计图”,将个体极端数据引发的问题融入到整体分析的大背景中,从整体到个体,从个体再到整体,在辩证地分析数据的过程中,学生客观真实地认识自己、了解他人。
三、 在数据分析中萌发人生的智慧
[教学片段三]
师:12岁时,男生的平均身高是148厘米,女生的平均身高是150厘米,预测一下,13岁时,他们的平均身高会有怎样的变化呢?为什么?
生:我估计男、女生的平均身高差不多都会增加6厘米,因为11岁到12岁时,他们都增高了6厘米。
……
师:20岁时,会怎样呢?
生:我知道男生的平均身高一定会比女生高。
……
师:40岁时,会怎样呢?
生:我估计平均身高应该不会有什么变化,即使有变化的话,变化也不会太大,因为40岁的时候人的身高已经定型了。
师:那么70岁时,又会怎样呢?
生:我认为到了老年,人的身高不仅不会增加,还会减少!
(出示某人从10岁到70岁的身高变化统计图)
师:大家分析得很有道理,在人的一生中,我们的身高先是呈上升趋势,接着呈平缓趋势,最后呈下降趋势。这里的起起落落是一种自然的规律,在我们的学习、生活过程中时常也会看到这样的现象,有时学习状态很好,而有时学习成绩不佳;有时很高兴,而有时却很伤心,古人说:人有悲欢离合——
生:月有阴晴圆缺,此事古难全。
师:是的,在人生旅途中,我们很难一帆风顺,也许你会遇到这样或者那样的困难,但只要我们以积极向上的心态去看待它们,一切就会变得更加美好。
“智慧数学”倡导者陈士文认为,“数学是一种理性精神,其中蕴藏一种至真至通的智慧。”理性中蕴含着智慧,这里不仅有学习的智慧,也有生活的智慧,更有人生的智慧。为此,我们要在数据分析的过程中注入理性的因子,将知识的学习与人生的价值进行有机结合。在上面的教学中,学生通过统计图认识到了身高变化的规律,在此基础上,教师带领学生从知识的习得逐渐走向人生的感悟,借助古人的观点——“人有悲欢离合,月有阴晴圆缺,此事古难全”,引发了学生情感上的共鸣,他们从中得到启发:在人生旅途中,我们很难一帆风顺,也许你会遇到这样或者那样的困难,但只要我们以积极向上的心态去看待它们,一切会变得更加美好。由此,学生在数据的分析过程中,多了一份豁达与从容,多了一份淡定与冷静,也多了一份对美好生活的追求。
数学的永恒主题是认识世界、认识自己,而这离不开理性的探索精神。回到统计的教学,除了数据分析过程中须要渗透理性精神之外,搜集数据要真实、描述数据要合理、运用数据要有度,这无不体现了理性精神的存在。有了理性,学生在统计中体验到了整体与部分、量变与质变、普适性与特殊性的辩证关系;有了理性,学生在统计中形成了相应的独立、准确、公正、严谨以及合理的精神意识;有了理性,学生在统计中感悟了求真、通达、化转的人生智慧。
【责任编辑:陈国庆】

